? ? ? ?本模型基于雙層優化框架，利用KKT條件、大M法、對偶理論求解，專注于綜合能源系統（微電網）多電源容量優化配置的模型介紹。代碼采用CPLEX求解器，注釋詳盡，非常適合新手學習該類問題的建模與求解思路。

模型總體原理：

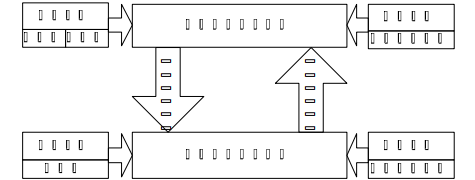
該模型的核心思想是將復雜的綜合能源系統規劃問題分解為兩個相互關聯的決策層面：

1. 上層規劃問題 (Investment/Planning Level):?負責長期投資決策。目標是確定系統中各類能源設備（如光伏PV、風機WT、儲能ESS等）的最佳安裝容量，使得整個規劃周期內的總成本（設備投資成本 + 運行維護成本）最低。

2. 下層運行問題 (Operation/Dispatch Level):?負責短期運行決策。在給定的設備容量（由上層的決策變量決定）下，目標是優化系統在一個典型運行周期（如一天、一周）內的運行策略（如發電機出力、儲能充放電、購售電），使得該周期內的運行成本（購電成本 + 售電收益 + 燃料成本（如有燃氣輪機）+ 其他可變運行成本）最低。

這兩個層級通過容量變量緊密耦合：

• 上層的容量決策 (Cap_PV,?Cap_WT,?Cap_ESS?等) 是下層運行優化問題的輸入參數或約束條件。

• 下層的運行成本是上層總成本目標函數的重要組成部分。

求解策略：?直接求解雙層優化問題通常非常困難。該模型采用數學變換將其轉化為一個單層混合整數線性規劃 (MILP)?問題：

1. 利用KKT條件：?將下層運行優化問題（通常是一個線性規劃LP）的最優性條件（KKT條件）寫出來。KKT條件包含：

   • 原始可行性:?下層運行約束必須滿足。

   • 對偶可行性:?下層拉格朗日函數的梯度條件。

   • 互補松弛條件:?原始約束和對偶變量之間滿足互補關系。

2. 處理互補松弛條件 (使用大M法)：?互補松弛條件是雙線性項（對偶變量 * 約束松弛量），是非凸的。大M法引入輔助二元變量和足夠大的常數?M，將這些非線性互補條件等價地轉化為一組線性約束和二元變量約束。

3. 整合目標函數：?將上層目標函數（包含投資成本和下層運行成本）與經過KKT條件和大M法轉換后的下層約束整合到一起，形成一個大型的單層MILP問題。

4. 對偶理論（輔助）：?在推導KKT條件中的對偶可行性部分時，會用到線性規劃的對偶理論，以確保轉換的正確性。

最終模型是一個包含連續變量、二元變量、線性目標函數和線性約束的MILP問題，可以使用高效的商業求解器如CPLEX進行求解。

部分程序實例：

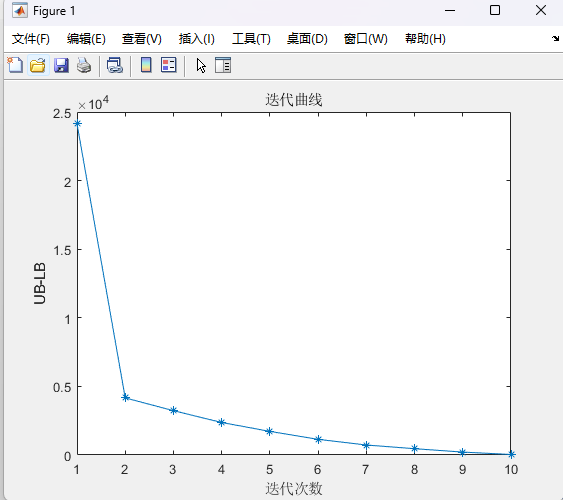
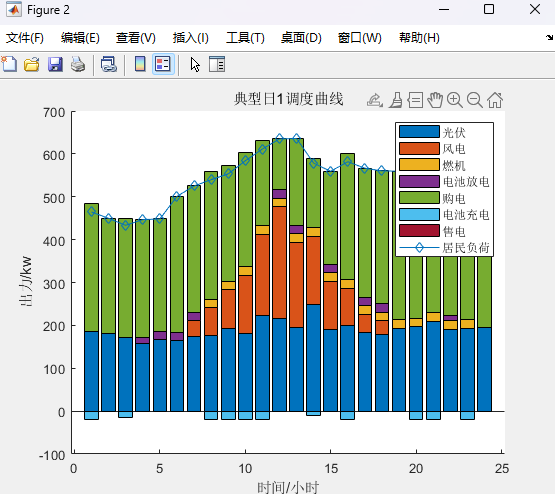
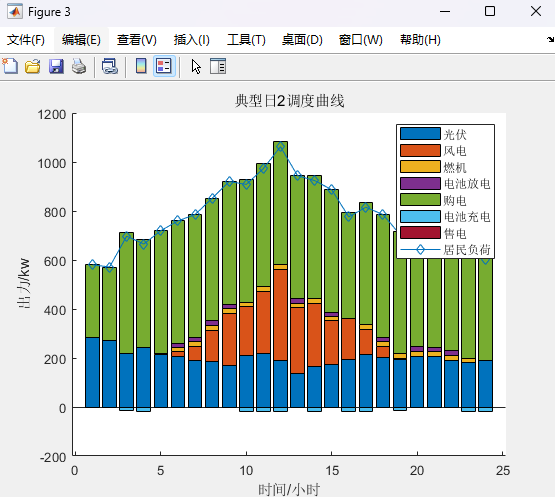
%% 考慮四種典型日下的雙層規劃clcclearwarning offclose alltic%% 設置參數canshu;%% 初始值%% 上層%初始折現成本+投資成本+購售電成本和燃料成本 +運維成本%LB為初始折現成本+投資成本+購售電成本+燃料成本 +運維成本%yita購售電成本+燃料成本+運維成本[yita,LB,ee_bat_int, p_wt_int,p_pv_int,p_g_int] = UP_1(rp,rbat,rPV,rWT,rG);%% 下層%UB為上層（折現成本+投資成本）+下層（購售電成本+燃料成本 +運維成本）[p_wt,p_pv,p_load,x,UB,p_g,p_ch,p_dis,p_buy,p_sell] = DOWN_(ee_bat_int,p_wt_int,p_pv_int,p_g_int,LB,yita);%UB1為初始上層（折現成本+投資成本）+下層（購售電成本+燃料成本 +運維成本）UB1 = UB;%% p為上層（購售電成本+燃料成本 +運維成本）與下層（購售電成本+燃料成本 +運維成本）差p(1)= UB - LB;e=100;%收斂度%% 開始迭代for k=1:Imax%% 上層 在已知光伏，風電，負荷出力（由下層傳遞到上層）計算初始折現成本+投資成本+購售電成本和燃料成本 +運維成本（求最小值）[yita,LB,ee_bat_int,p_wt_int,p_pv_int,p_g_int] = UP_2(p_wt,p_pv,p_load);%MP迭代%% 下層 已知（折現成本+投資成本，由上層傳遞到下層）+計算（購售電成本+燃料成本 +運維成本）[p_wt,p_pv,p_load,x,UB,p_g,p_ch,p_dis,p_buy,p_sell] = DOWN_(ee_bat_int,p_wt_int,p_pv_int,p_g_int,LB,yita);%SP迭代UB = min(UB1,UB);%取UB較小值%% p為上層（購售電成本+燃料成本 +運維成本）與下層（購售電成本+燃料成本 +運維成本）差p(k+1) = UB-LB;%判斷是否收斂if abs(p(k+1))<=ebreakendend%% 輸出結果%儲能,購電,風電,光伏,負荷,燃機p_wtp_pvp_loadp_gp_chp_disp_buyp_selltoc%% 畫圖%% 迭代figure;plot(p,'-*')xlabel('迭代次數')ylabel('UB-LB')title('迭代曲線')%% 典型日1figurehold onpositive=[p_wt(:,1),p_pv(:,1),p_g(:,1),p_dis(:,1),p_buy(:,1)];negative=[-p_ch(:,1),-p_sell(:,1)];bar(positive,'stack')bar(negative,'stack')plot(p_load(:,1),'-d')ylabel('出力/kw')xlabel('時間/小時')title('典型日1調度曲線')legend('光伏','風電','燃機','電池放電','購電','電池充電','售電','居民負荷')

輸出結果:

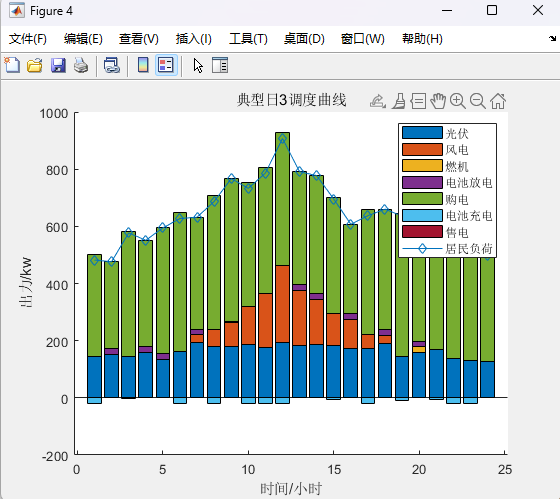
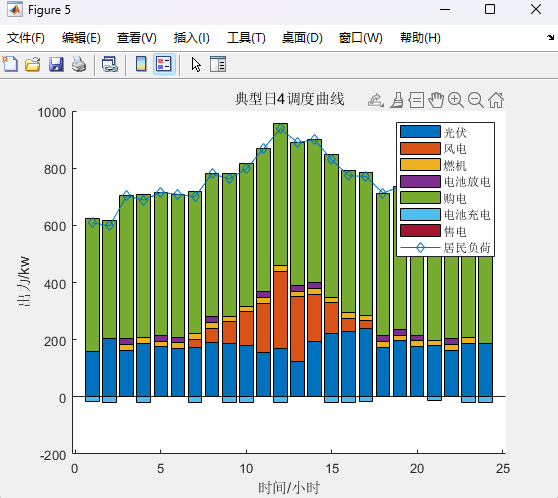
總結:

該模型通過雙層優化結構清晰地區分了長期規劃（容量決策）和短期運行（調度決策）。利用KKT條件刻畫下層最優性，借助大M法處理非線性的互補松弛條件，并運用對偶理論確保轉換正確，最終將復雜的雙層問題轉化為一個可被CPLEX高效求解的單層混合整數線性規劃(MILP)問題。其輸出提供了微電網建設的最佳多電源容量配置方案 (Cap_PV,?Cap_WT,?Cap_ESS) 以及在該配置下成本最優的運行策略。注釋齊全的代碼為學習這種建模與求解方法提供了寶貴的實踐材料。

仿真程序模型詳情見原文鏈接：

https://mp.weixin.qq.com/s/kX85ZaK1o_B35QHQRtq_Cw