1.題目鏈接
LeetCode盛最多的水
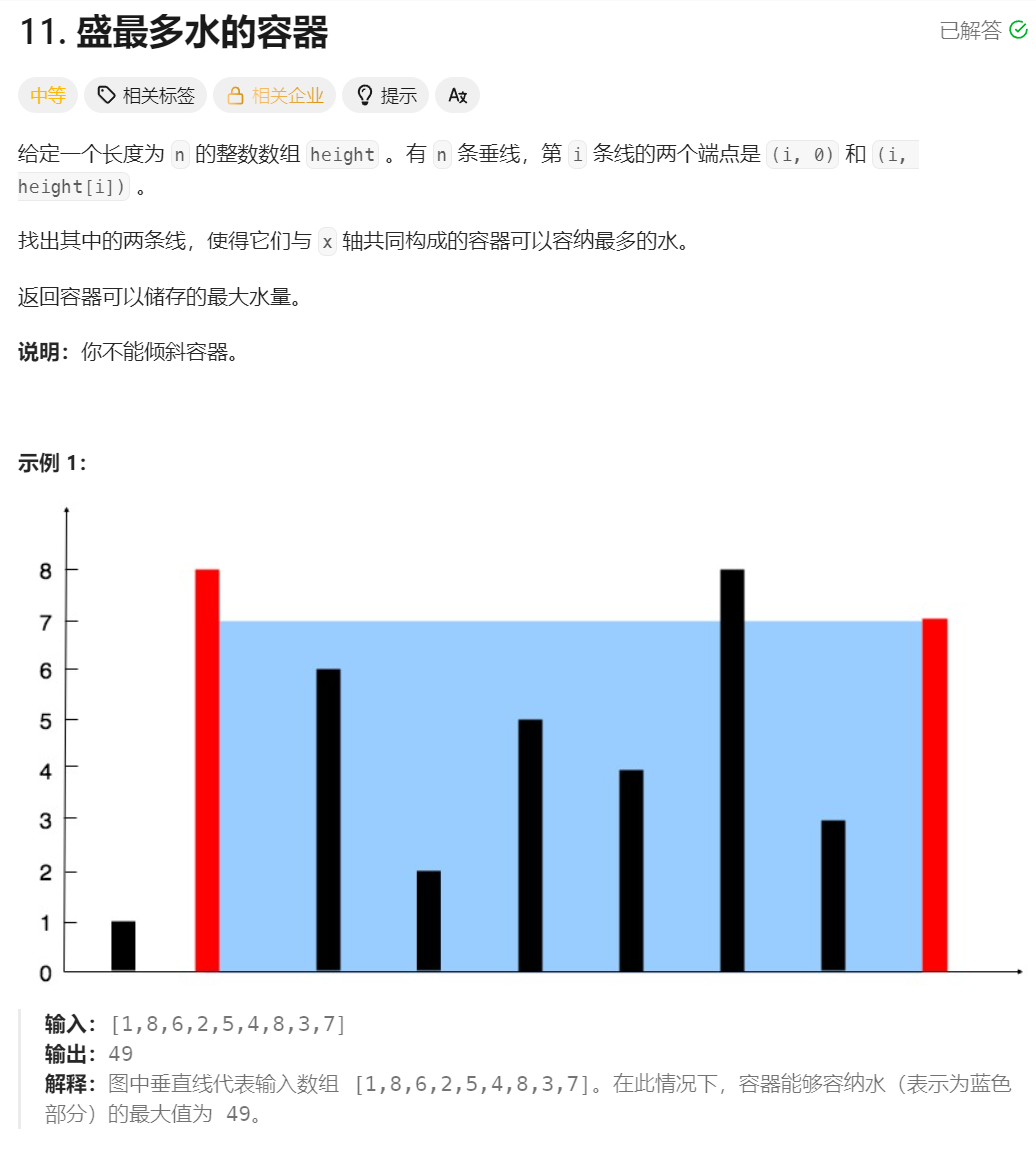
2.題目描述
3.題目解析?
問題本質分析
"盛最多水的容器" 問題可以抽象為:在坐標軸上有 n 條垂直線段,第 i 條線段的兩個端點分別是 (i, 0) 和 (i, height [i])。找到兩條線段,使得它們與 x 軸共同構成的容器能夠容納最多的水。
容器的容量計算公式是:面積 = 寬度 × 高度,其中:
- 寬度 = 兩條線段的橫坐標之差
- 高度 = 兩條線段中較短那條的長度(因為水會從較短的一邊溢出)
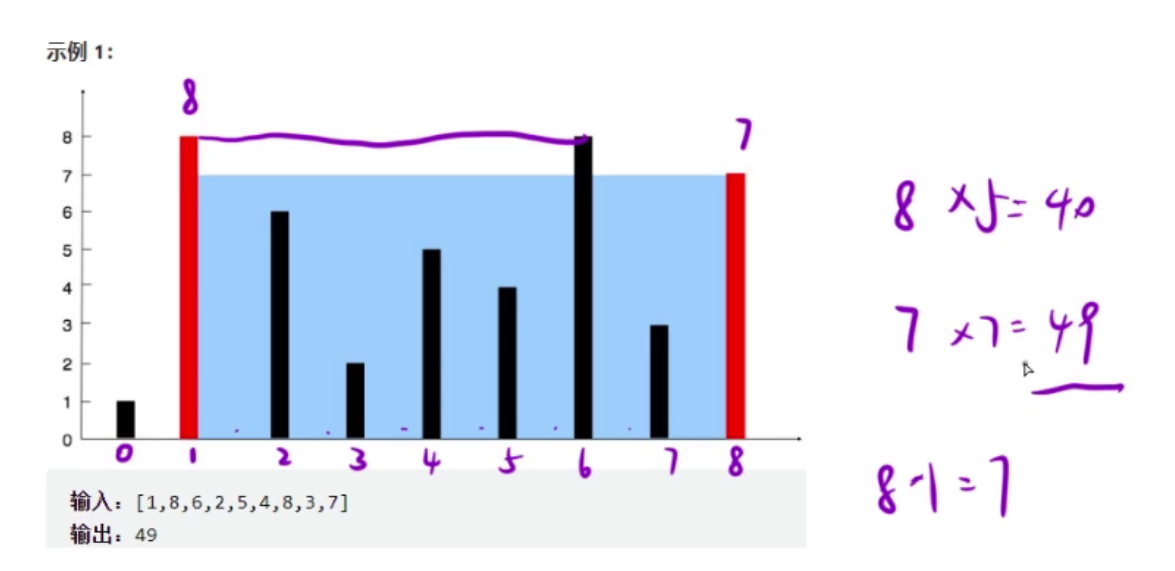
算法核心思路
采用雙指針從兩端向中間移動,通過貪心策略每次選擇可能獲得更大面積的移動方向:
- 初始狀態:左指針在最左端 (left=0),右指針在最右端 (right=height.size ()-1)
- 計算當前面積:以當前雙指針為邊界計算容器面積
- 更新最大面積:如果當前面積大于歷史最大值,則更新
- 移動指針:
- 若左指針指向的線段更短,移動左指針 (left++)
- 否則,移動右指針 (right--)
- 終止條件:左右指針相遇 (left>= right)
?下面我們畫圖理解:
1.定義兩個指針分別從左右兩端開始,計算當前的V
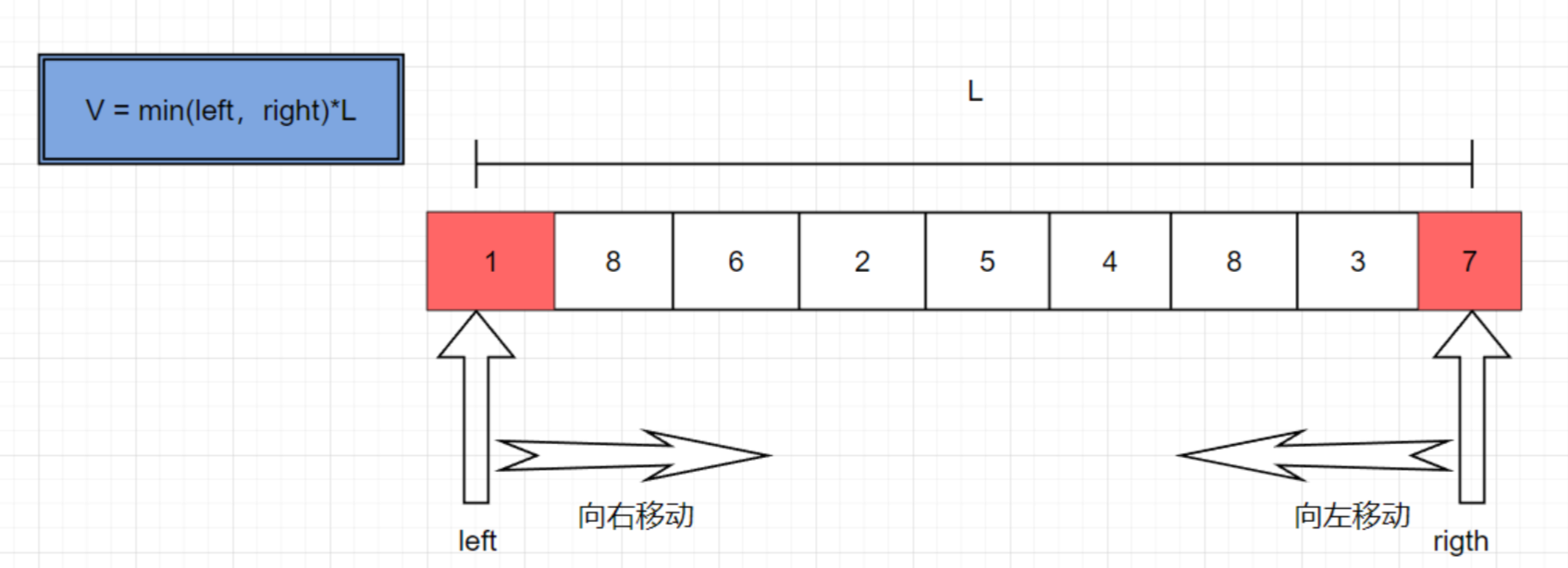
2.接著開始移動指針?
如果移動right,L會減小,H也會減小,則V一定減小,所以沒必要這么做.?
?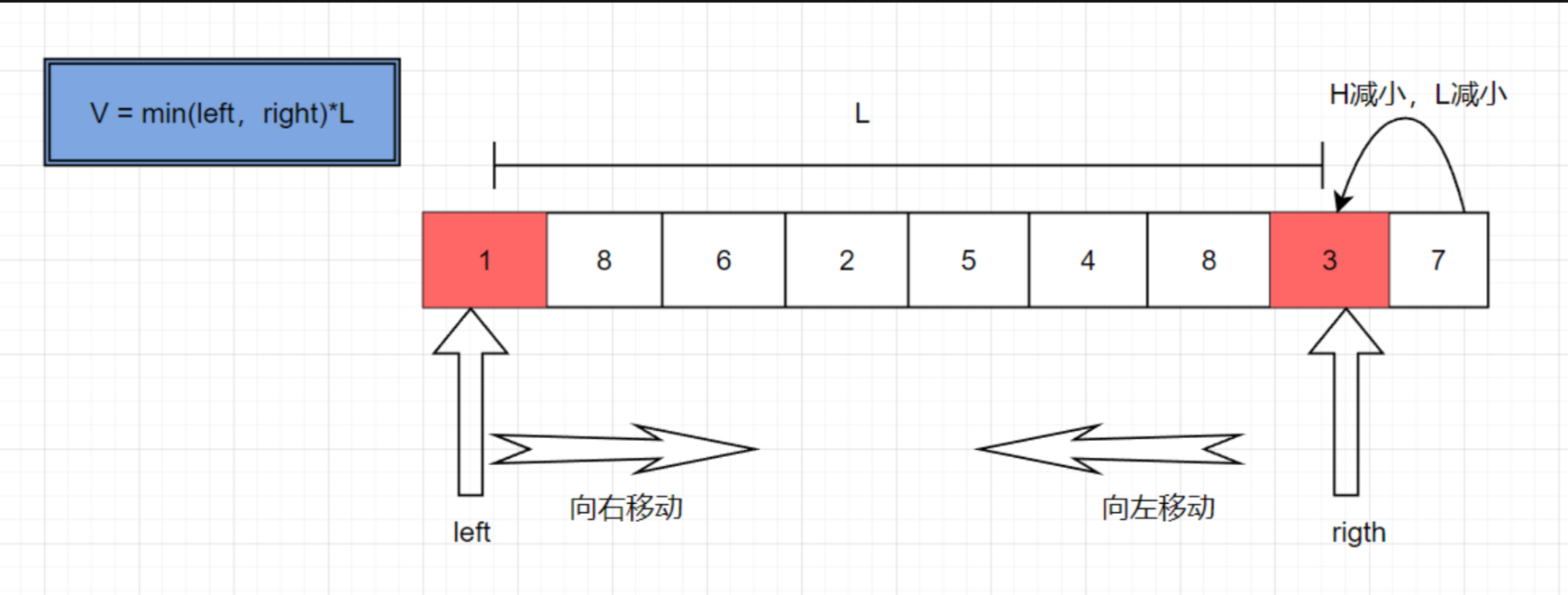
如果移動left,L會增大,H會減小,但V有可能增大?
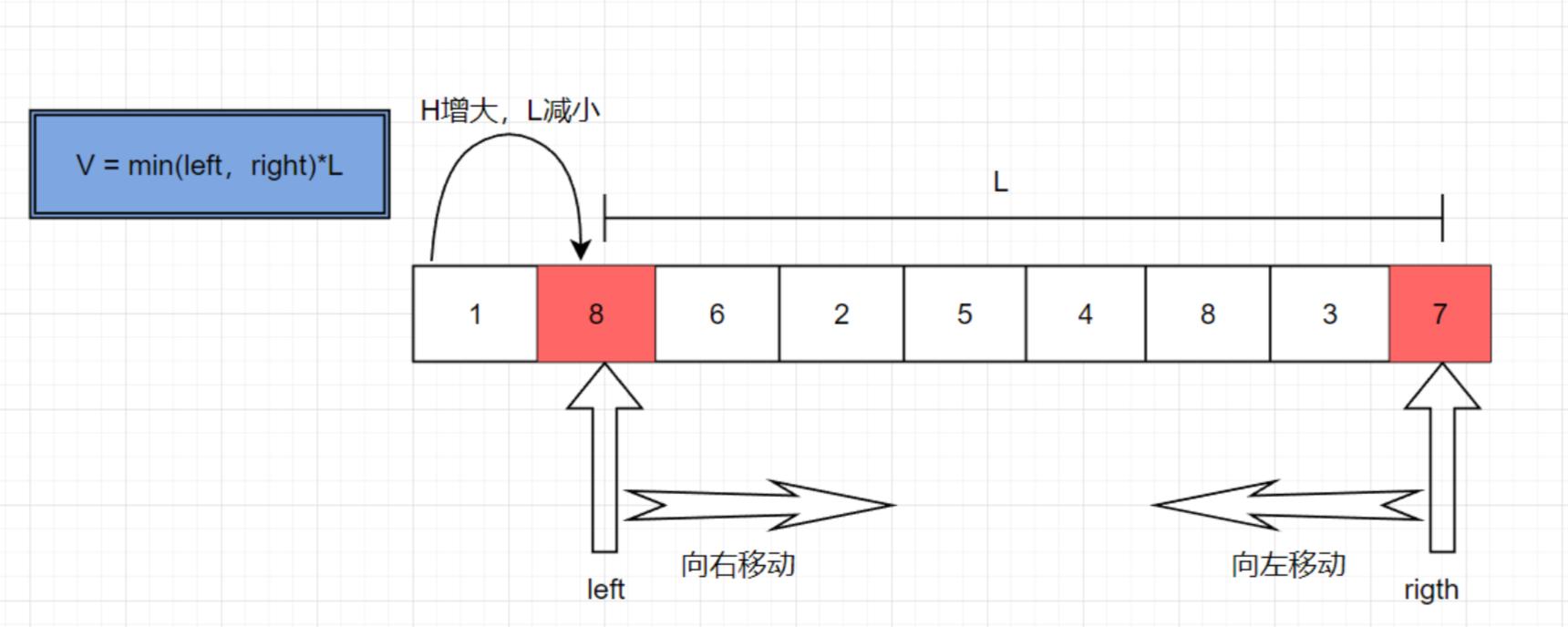
為什么這樣移動指針是正確的?
這是理解算法的關鍵。假設我們有兩個指針 left 和 right,且 height [left] < height [right]:
- 如果我們移動右指針,新的寬度一定減小(因為 right-left 變小)
- 新的高度取決于新的 right' 和原 left 中的較小值,由于原 left 是較短的,新高度不會超過原高度
- 因此,移動右指針只會得到更小的面積,不可能得到更大的面積
反之,如果 height [right] 更短,移動左指針也會導致面積減小。因此,只有移動較短的指針才有可能獲得更大的面積,這是一種貪心策略的體現。
這種雙指針解法的優勢在于:
- 時間效率高:只需遍歷一次數組,O (n) 時間復雜度
- 空間效率高:只使用常數級額外空間,O (1) 空間復雜度
- 思路簡潔:通過貪心策略每次做出局部最優選擇,最終得到全局最優解
這個算法充分體現了貪心算法的思想 —— 通過每一步的局部最優選擇,最終達到全局最優。
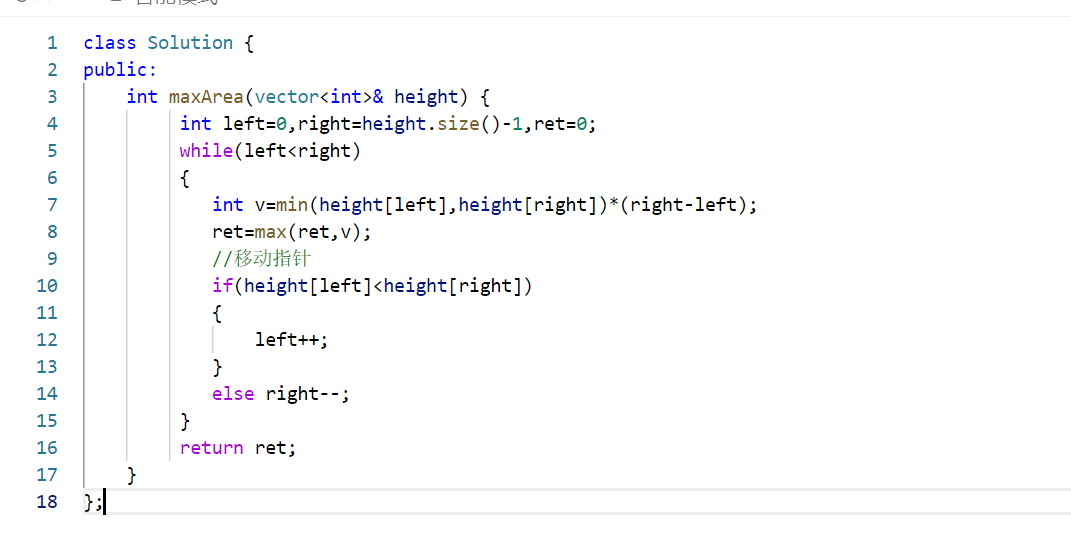
完整代碼:?
?
代碼注釋:?
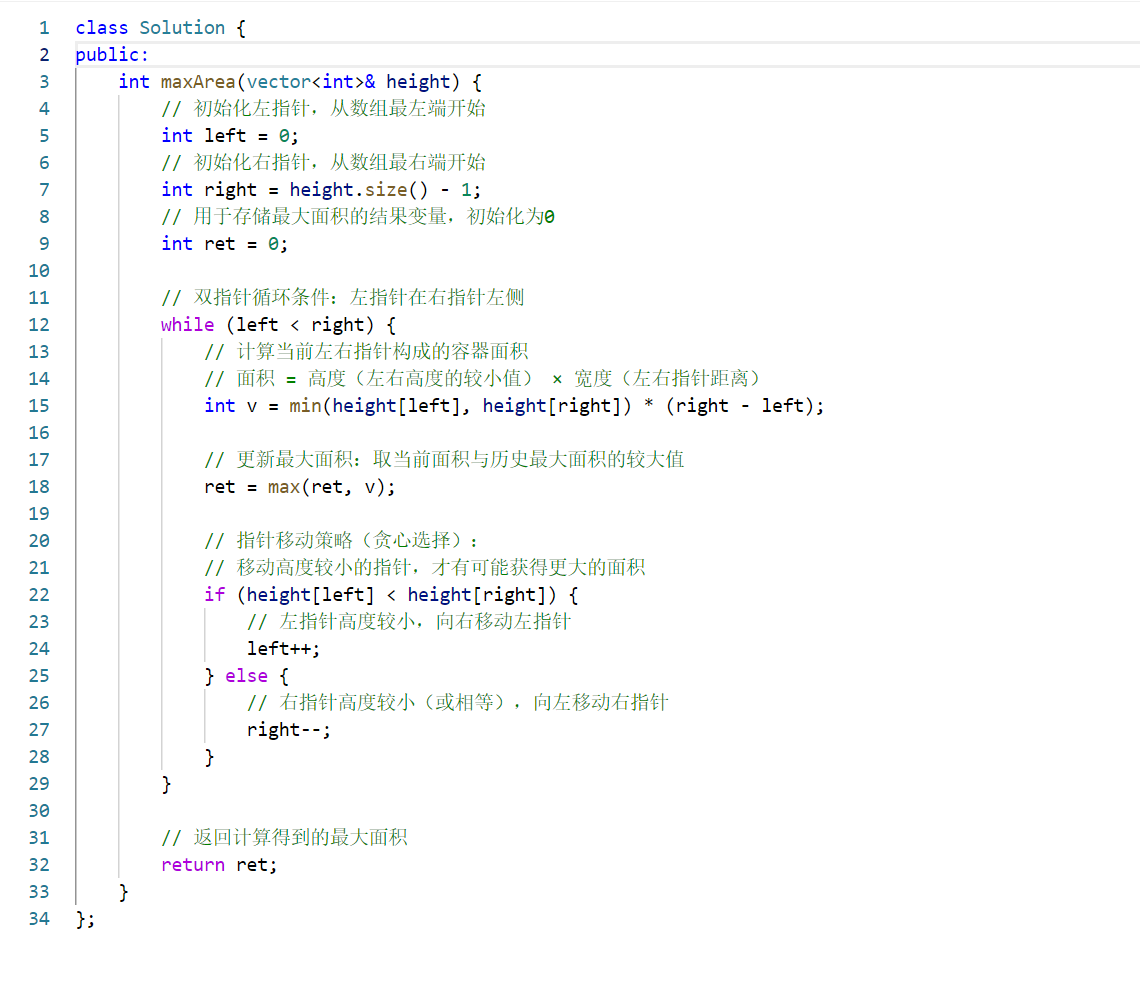
復雜度分析?
該雙指針解法在時間和空間上都達到了最優:
- 時間復雜度:O (n)(線性時間,遍歷一次數組)
- 空間復雜度:O (1)(常數空間,不依賴輸入規模)
這也是該算法被認為是「盛最多水的容器」問題最優解的核心原因 —— 在保證正確性的前提下,實現了極高的效率。


)
)
雙向鏈表)



等級考試試卷(一級))



)






