在擴散模型中，逆向過程的目標是從噪聲數據逐步恢復出原始數據。本文將詳細解析逆向條件分布 $q({\mathbf{z}}_{t?1}\mid {\mathbf{z}}_t,\mathbf{x})$的推導過程，揭示擴散模型如何通過高斯分布實現數據重建。

---

1. 核心問題

在擴散模型中，我們希望學習如何從含噪數據 $({\mathbf{z}}_t$) 逐步恢復原始數據 $\mathbf{x}$。直接求逆向分布 $q({\mathbf{z}}_{t?1}\mid {\mathbf{z}}_t)$ 是困難的，但若額外已知原始數據 $\mathbf{x}$，則條件分布 $q({\mathbf{z}}_{t?1}\mid {\mathbf{z}}_t,\mathbf{x})$可以簡化為高斯分布。

---

2. 貝葉斯定理的應用

利用貝葉斯定理，將條件分布分解為：
$$q({\mathbf{z}}_{t?1}\mid {\mathbf{z}}_t,\mathbf{x})=\frac{q({\mathbf{z}}_t\mid {\mathbf{z}}_{t?1},\mathbf{x})q({\mathbf{z}}_{t?1}\mid \mathbf{x})}{q({\mathbf{z}}_t\mid \mathbf{x})}$$

關鍵簡化：

• 馬爾可夫性質：前向過程中，${\mathbf{z}}_t$僅依賴${\mathbf{z}}_{t?1}$，因此：
  $$q({\mathbf{z}}_t\mid {\mathbf{z}}_{t?1},\mathbf{x})=q({\mathbf{z}}_t\mid {\mathbf{z}}_{t?1})$$
  此項由前向過程的定義給出（公式 20.4）：
  $$q({\mathbf{z}}_t\mid {\mathbf{z}}_{t?1})=\mathcal{N}\left({\mathbf{z}}_t;\sqrt{1?{\beta }_t}{\mathbf{z}}_{t?1},{\beta }_t\mathbf{I}\right)$$

• 擴散核：$q({\mathbf{z}}_{t?1}\mid \mathbf{x})$是前向過程的閉式解（公式 20.6）：
  $$q({\mathbf{z}}_{t?1}\mid \mathbf{x})=\mathcal{N}\left({\mathbf{z}}_{t?1};\sqrt{{\alpha }_{t?1}}\mathbf{x},(1?{\alpha }_{t?1})\mathbf{I}\right)$$
  其中${\alpha }_{t?1}={\prod }_{s=1}^{t?1}(1?{\beta }_s)$。

• 分母的忽略：分母 $q({\mathbf{z}}_t\mid \mathbf{x})$ 與${\mathbf{z}}_{t?1}$無關，可視為常數。

---

3. 高斯分布的推導

分子部分是兩個高斯分布的乘積：
$$q({\mathbf{z}}_t\mid {\mathbf{z}}_{t?1})?q({\mathbf{z}}_{t?1}\mid \mathbf{x})$$
通過配方法（completing the square），可以合并指數項，得到一個新的高斯分布：
$$q({\mathbf{z}}_{t?1}\mid {\mathbf{z}}_t,\mathbf{x})=\mathcal{N}\left({\mathbf{z}}_{t?1};{\mathbf{m}}_t(\mathbf{x},{\mathbf{z}}_t),{\sigma }_t^2\mathbf{I}\right)$$

均值和方差的計算：

• 均值 (\mathbf{m}_t)：
  $${\mathbf{m}}_t(\mathbf{x},{\mathbf{z}}_t)=\frac{\sqrt{{\alpha }_{t?1}}{\beta }_t}{1?{\alpha }_t}\mathbf{x}+\frac{\sqrt{1?{\beta }_t}(1?{\alpha }_{t?1})}{1?{\alpha }_t}{\mathbf{z}}_t$$
  這是原始數據$\mathbf{x}$和當前噪聲數據${\mathbf{z}}_t$的線性組合。

• 方差 ${\sigma }_t^2$：
  $${\sigma }_t^2=\frac{(1?{\alpha }_{t?1}){\beta }_t}{1?{\alpha }_t}$$
  僅依賴噪聲調度參數${\beta }_t$和累積系數${\alpha }_t$。

---

4. 直觀理解

• 給定$\mathbf{x}$的重要性：若已知原始數據$\mathbf{x}$，則從 ${\mathbf{z}}_t$推斷 ${\mathbf{z}}_{t?1}$是一個確定性更強的去噪問題，解為高斯分布。
• 物理意義：均值 ${\mathbf{m}}_t$是“部分去噪”的結果，方差 ${\sigma }_t^2$表示剩余的不確定性。

---

5. 與逆向過程的關系

實際訓練中，我們無法直接使用 $\mathbf{x}$（因需生成新數據），因此：

1. 用神經網絡 $p_{\theta }({\mathbf{z}}_{t?1}\mid {\mathbf{z}}_t)$近似$q({\mathbf{z}}_{t?1}\mid {\mathbf{z}}_t,\mathbf{x})$。
2. 網絡通過預測均值 ${\mathbf{m}}_t$ 或噪聲 $?$來學習去噪。

---

6. 總結

• 數學本質：通過貝葉斯定理和高斯分布的性質，顯式推導出條件逆向分布的閉式解。
• 實際意義：指導神經網絡學習去噪步驟的理論基礎。
• 關鍵公式：
  $$q({\mathbf{z}}_{t?1}\mid {\mathbf{z}}_t,\mathbf{x})=\mathcal{N}\left({\mathbf{z}}_{t?1};{\mathbf{m}}_t(\mathbf{x},{\mathbf{z}}_t),{\sigma }_t^2\mathbf{I}\right)$$

這種推導是擴散模型理論的核心，確保了從噪聲中生成數據的數學嚴謹性。

---

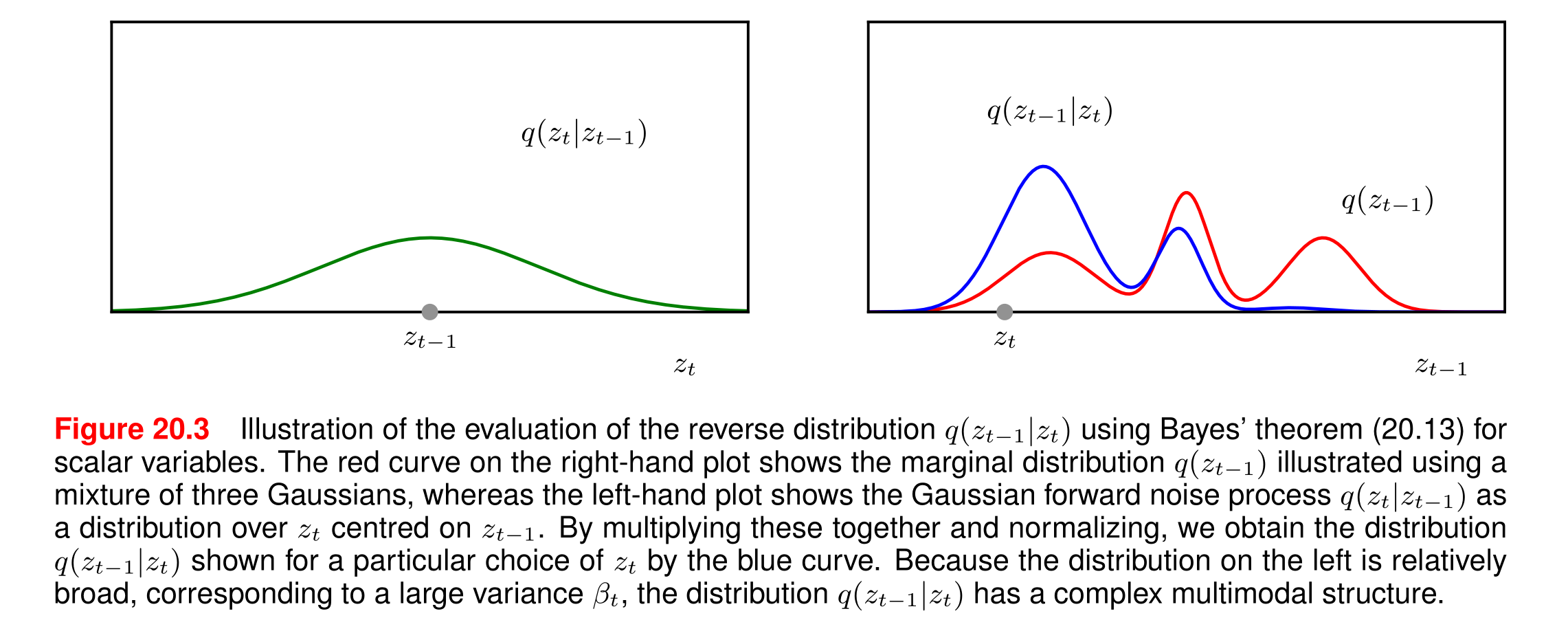
這張圖（圖20.3）展示了擴散模型中逆向分布的計算過程，以下是詳細解析：

---

1. 圖的組成與含義

(1) 左子圖：前向噪聲過程$q(z_t|z_{t?1})$

• 橫軸：噪聲數據 $z_t$
• 縱軸：概率密度
• 曲線特征：以 $z_{t?1}$為中心的高斯分布（鐘形曲線）
• 關鍵參數：方差${\beta }_t$較大 → 曲線"寬泛"（平坦）
• 物理意義：表示單步加噪時，$z_t$ 可能取值的范圍較大

(2) 右子圖：邊緣分布$q(z_{t?1})$

• 橫軸：數據 $z_{t?1}$
• 縱軸：概率密度
• 紅色曲線：三個高斯分布的混合（多峰結構）
• 物理意義：反映數據在$t?1$ 步的整體分布（可能對應不同模態的真實數據）

(3) 藍色曲線：逆向分布$q(z_{t?1}|z_t)$

• 生成方式：通過貝葉斯定理將左、右子圖的分布相乘并歸一化
• 特征：復雜多峰結構（多個局部最大值）
• 物理意義：給定當前噪聲$z_t$，可能對應多個潛在的 $z_{t?1}$狀態

---

2. 關鍵句解析

“由于左側分布（對應大方差βt）相對寬泛，導致逆向分布$q(zt?1|zt)$呈現出復雜的多峰結構。”

(1) 因果關系

• 大方差 ${\beta }_t$ → 前向分布 $q(z_t|z_{t?1})$ 平坦 → 允許 $z_t$ 偏離 $z_{t?1}$更遠
• 結果：一個 $z_t$可能由多個不同的$z_{t?1}$生成 → 逆向分布出現多峰

(2) 多峰結構的含義

• 每個峰：對應一個可能的$z_{t?1}$ 來源
• 示例：若原始數據包含"貓"和"狗"兩類，加噪后的$z_t$可能無法確定源自哪類 → 逆向分布同時保留兩種可能

(3) 數學解釋

貝葉斯定理中：
$$q(z_{t?1}|z_t)\propto \underset{\text{寬泛分布}}{\underbrace{q(z_t|z_{t?1})}}?\underset{\text{多峰分布}}{\underbrace{q(z_{t?1})}}$$

• 寬泛的似然$q(z_t|z_{t?1})$不會壓制$q(z_{t?1})$ 的多峰性
• 最終逆向分布繼承$q(z_{t?1})$ 的多峰特征

---

3. 對擴散模型的意義

1. 理論挑戰：多峰性說明直接計算逆向分布極其困難
2. 解決方案：
   • 用神經網絡$p_{\theta }(z_{t?1}|z_t)$近似為單峰高斯
   • 通過訓練使網絡學會選擇"最可能"的峰（對應高質量生成）
3. 設計啟示：
   • 需控制${\beta }_t$大小：方差過大導致多峰性增強，訓練難度增加
   • 多峰性也賦予模型捕捉數據多樣性的能力

---

4. 實例說明

假設：

• 右子圖的三個峰對應$z_{t?1}=?1,0,1$（三種潛在狀態）
• 觀測到$z_t=0.5$（左子圖中心在某個 $z_{t?1}$
• 藍色曲線可能在$z_{t?1}=0$和$z_{t?1}=1$處各有一個峰
  → 說明$z_t=0.5$可能由$z_{t?1}=0$或$1$ 加噪得到

---

5. 總結

該圖揭示了擴散模型中逆向過程的本質困難：
前向噪聲的隨機性（大方差）導致逆向推斷存在歧義，而模型必須通過學習解決這種歧義，才能實現高質量生成。這一現象也解釋了為什么擴散模型需要復雜的網絡結構和訓練技巧。

---

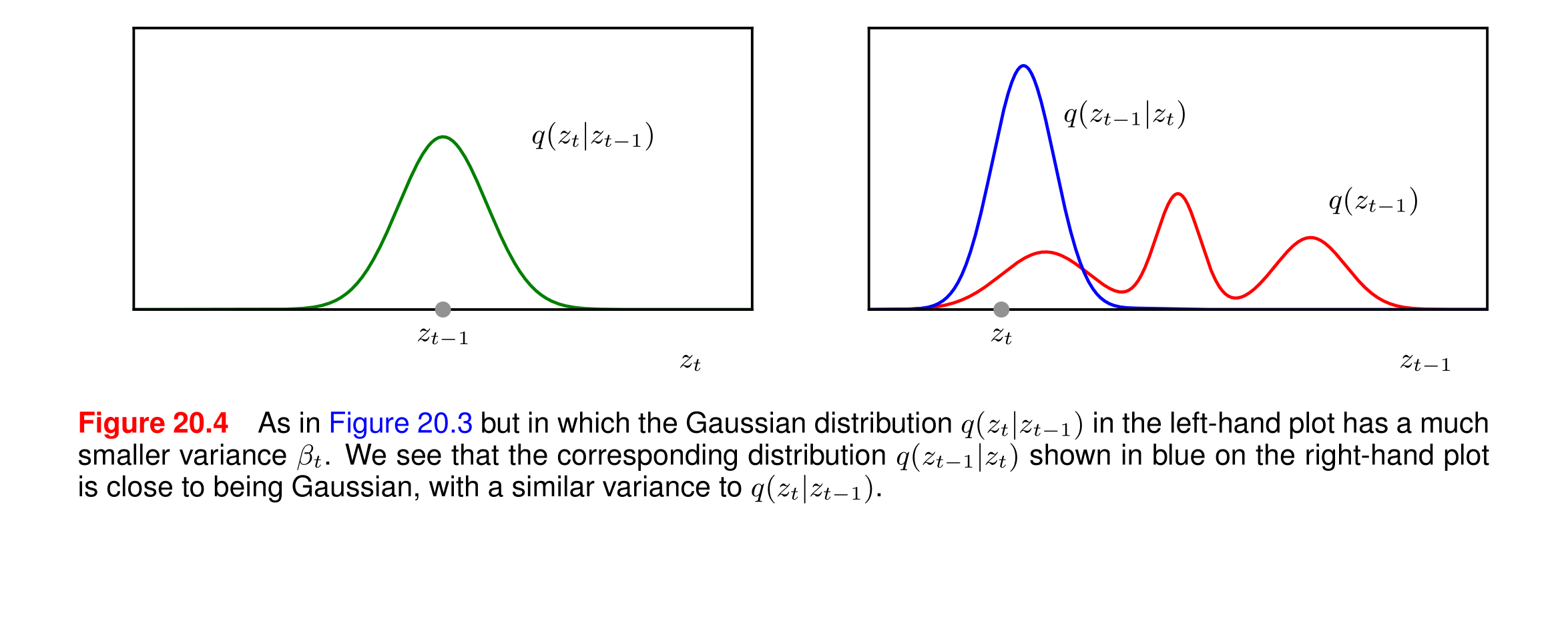
在圖20.4中，左圖展示了條件概率分布$q(z_t|z_{t?1})$，其方差${\beta }_t$較小，這意味著分布更窄。右圖展示了相應的逆過程分布$q(z_{t?1}|z_t)$。

為什么分布更窄并不意味著變化更明顯？

1. 方差與變化幅度：

   • 方差是衡量數據分布的離散程度的指標。較小的方差意味著數據點更集中在均值附近。
   • 在條件概率分布 $q(z_t|z_{t?1})$中，較小的方差表示在給定 $z_{t?1}$ 的情況下， $z_t$ 的取值更集中在某個特定值附近，即 $z_t$ 的變化幅度較小。

2. 逆過程分布：

   • 右圖中的藍色曲線 $q(z_{t?1}|z_t)$展示了在給定 $z_t$的情況下， $z_{t?1}$ 的分布。
   • 由于左圖中的 $q(z_t|z_{t?1})$ 分布較窄，意味著 $z_t$ 的取值相對集中，因此在逆過程中， $z_{t?1}$ 的分布也相對集中，接近高斯分布。

3. 變化幅度與學習難度：

   • 分布更窄意味著在每一步變換中，潛在變量的變化幅度較小。這種微小的變化使得模型更容易學習如何逆轉這些變換，因為每一步的變換都是可預測的、穩定的。
   • 如果方差較大，潛在變量的變化幅度會更大，這會增加模型學習逆過程的難度，因為每一步的變換更加不可預測。

總結

• 分布更窄（方差較小）意味著潛在變量的變化幅度較小，而不是變化更明顯。
• 這種微小的變化使得逆過程更容易學習和預測，因為每一步的變換都是相對穩定和可預測的。
• 因此，較小的方差有助于簡化模型的學習過程，但可能需要更多的步驟來達到顯著的總體變化。