面試高頻題力扣 417. 太平洋大西洋水流問題洪水灌溉(FloodFill) 深度優先遍歷(dfs) 暴力搜索 C++解題思路每日一題

零、題目描述：用人話再講一遍
一、為什么這道題值得咱們學習？
二、思路探索
- 常規思路：逐個檢查每個格子（會超時！??）
三、正難則反：反向思維的巧妙應用 🔄
（思考時間！）💡
四、代碼實現：一步步拆解
- 代碼拆解:
- 時間復雜度分析
- 空間復雜度分析
六、坑點總結 & 舉一反三 🚀

嗨，各位算法愛好者！今天咱們來討論一道有點繞但超經典的題目—— LeetCode 417. 太平洋大西洋水流問題。這道題堪稱“洪水灌溉”系列的進階版，學好它，能讓你的逆向思維能力上個大臺階！

零、題目描述：用人話再講一遍

在這里插入圖片描述

這道題力扣上面的題目表述太難評了，本來挺簡單的一道題讓力扣的描述說的好像一道外星題，我就不過多說明力扣的題目描述，用我自己的話來向大家解釋下這道題：

題目核心：
給你一個 m x n 的網格（可以想象成一個島嶼的地形圖）

每個坐標都有自己的高度值 🏔?
島嶼的上邊界和左邊界挨著太平洋 🌊
島嶼的下邊界和右邊界挨著大西洋 🌊
水往低處流或者平流（即水可以向<=自己高度值的坐標里流動）
這道題要我們返回的就是既能流到太平洋，又能流到大西洋的格子坐標。

舉個栗子 🌰：
如果一個格子的水，既能一路向左/向上流到太平洋，又能一路向右/向下流到大西洋，那它就是我們要找的目標！

我們用示例1來說明：👇

輸入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
輸出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

以坐標 [2,2]（第三行第三列，高度 5 ）為例，快速模擬驗證邏輯：

我們來以 [2,2]也就就是圖中最中間的5這個坐標模擬流水

先是流向太平洋：
[2,2] (5) → [1,2] (3)（上，3≤5）→ [0,2] (2)（上，2≤3）→ 觸達第 0 行（太平洋邊界）

之后是流大西洋：
[2,2] (5) → [3,2] (1)（下，1≤5）→ [4,2] (1)（下，1≤1）→ 觸達第 4 行（大西洋邊界）

這些黃色格子要么本身就在海洋邊界（直接滿足流向對應海洋），要么能通過 “向更低 / 等高單元格流動” 的規則，連通到太平洋或大西洋的邊界。通過這樣的水流邏輯，它們被判定為 “既能流向太平洋，又能流向大西洋”，所以出現在最終結果里。你可以結合網格圖，順著水流方向模擬一遍，就能更直觀理解啦～

一、為什么這道題值得咱們學習？

這道題簡直是逆向思維的絕佳教材！它的精髓在于：

打破“從起點找終點”的固定思維，學會“正難則反”（當正面求解復雜時，試試反過來想）
進一步鞏固洪水灌溉（Flood Fill） 算法的應用
訓練二維網格中“區域標記”與“交集計算”的能力

💡 悄悄說：這道題和咱們專欄中的第一篇博客力扣 200.島嶼數量是遞進關系哦！如果還沒看過建議先去看一看那一篇博客，講了DFS的基礎實現，我們專欄中的上一篇博客力扣 130. 被圍繞的區域則鋪墊了“正難則反”的思路，循序漸進效果更佳～感興趣的朋友可以訂閱我的專欄每日一題，我會每天發一篇關于算法練習的博客哦，專欄中的博客也都是有著層層遞進的聯系的~

二、思路探索

常規思路：逐個檢查每個格子（會超時！??）

最直觀的想法：遍歷每個格子，分別判斷它能否流到太平洋和大西洋。

步驟：

對每個格子 (i,j)，調用 canFlowToPacific(i,j) 和 canFlowToAtlantic(i,j)
兩個函數都返回 true 時，加入結果集

實現草圖：

// 檢查(i,j)能否流到太平洋
bool canFlowToPacific(int i, int j, vector<vector<int>>& heights) {if (i == 0 || j == 0) return true; // 已到達太平洋邊界for (四個方向) {int ni = i + dx[k], nj = j + dy[k];if ( heights[ni][nj] <= heights[i][j] ) { // 能往低處流if (canFlowToPacific(ni, nj, heights)) return true;}}return false;
}
// 大西洋同理...

為什么會超時？

每個格子可能被重復檢查多次，時間復雜度高達 O((m*n)^2)
對于 300x300 的網格，運算量會達到驚人的 8100 萬2，直接爆掉！

結果也是如此，我已經替大家試過了/(ㄒoㄒ)/~~
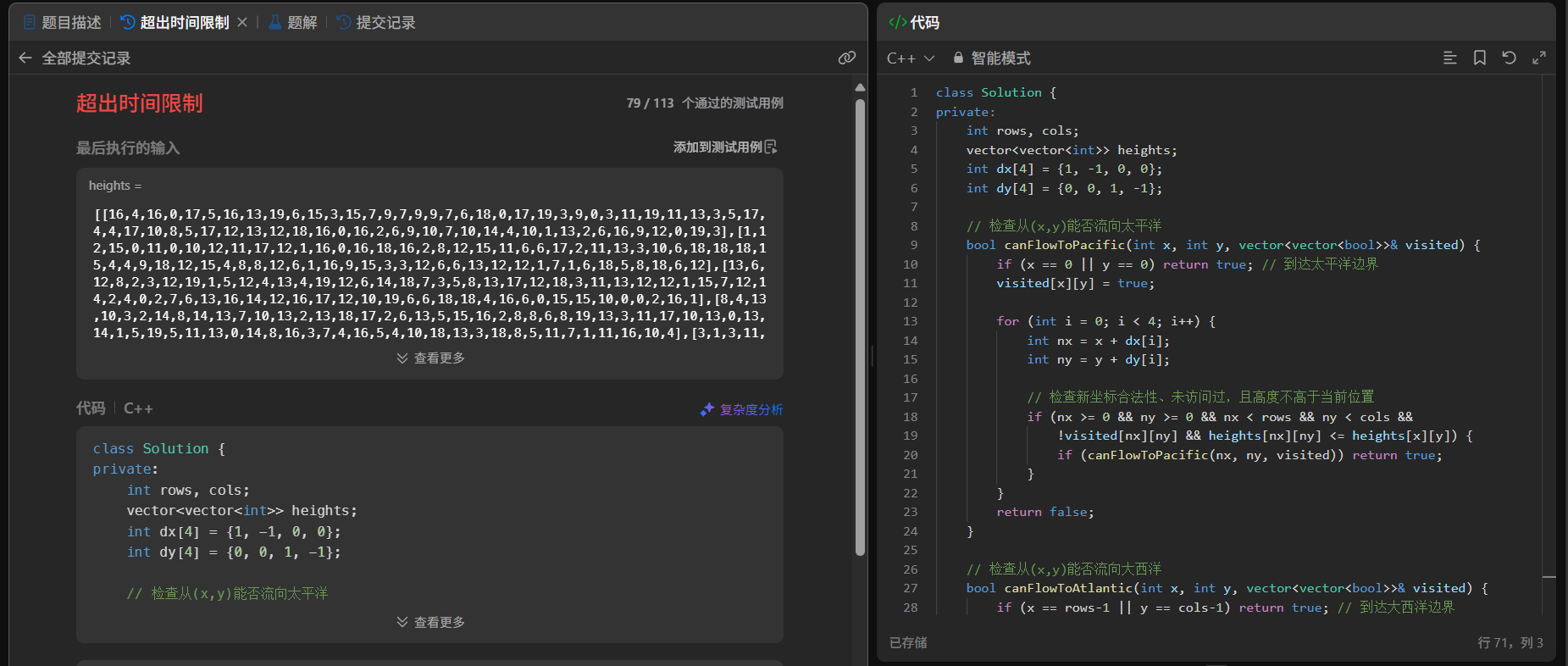
在這里插入圖片描述
所以說我們要換一個思路👇

三、正難則反：反向思維的巧妙應用 🔄

既然從格子往海洋流不好算，那咱們反過來想：從海洋往陸地“爬”！

核心邏輯：

太平洋的范圍：從所有能直接流入太平洋的邊界（上邊界 i=0、左邊界 j=0）出發，標記所有能逆流到達的格子（即這些格子的水可以流到太平洋）。
大西洋的范圍：從所有能直接流入大西洋的邊界（下邊界 i=rows-1、右邊界 j=cols-1）出發，標記所有能逆流到達的格子（即這些格子的水可以流到大西洋）。
結果：要是我們遍歷完這兩個范圍那么兩個范圍的重疊區域，就是既能流到太平洋又能流到大西洋的格子！

生動比喻 🌊??🏔?：
想象太平洋和大西洋的水在漲潮，水可以往高處漫（和自然規律相反，這里是“逆水行舟”）。最終，被兩邊的水都淹沒的地方，就是我們要找的答案～

步驟拆解：

第一步：用 Pmark 數組標記太平洋能“淹到”的格子
- 從 (0,j)（上邊界）和 (i,0)（左邊界）開始DFS
- 只有當相鄰格子更高或等高時，水才能漫過去
第二步：用 Amark 數組標記大西洋能“淹到”的格子
- 從 (rows-1,j)（下邊界）和 (i,cols-1)（右邊界）開始DFS
第三步：遍歷所有格子，同時被 Pmark 和 Amark 標記的就是結果

（思考時間！）💡

理解了“正難則反”的思路后，不妨先自己動手試試寫代碼？

如何初始化兩個標記數組？
DFS的遞歸條件應該怎么寫？
如何高效求兩個標記數組的交集？

先嘗試獨立實現，再看下面的代碼解析，收獲會更大哦～

四、代碼實現：一步步拆解

class Solution {
public:// 方向數組：上下左右（順序不影響，覆蓋四個方向即可）int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};int rows, cols; // 網格的行數和列數vector<vector<int>> result; // 存儲最終結果vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {// 邊界檢查：空網格直接返回if (heights.empty() || heights[0].empty()) return result;rows = heights.size();cols = heights[0].size();// 初始化標記數組：記錄能流到兩個海洋的格子vector<vector<bool>> Pmark(rows, vector<bool>(cols, false)); // 太平洋vector<vector<bool>> Amark(rows, vector<bool>(cols, false)); // 大西洋// 1. 標記太平洋的范圍// 左邊界（j=0）的所有格子for(int i = 0; i < rows; i++) {dfs(i, 0, heights, Pmark);}// 上邊界（i=0）的所有格子（注意：(0,0)已經被左邊界處理過，這里會重復調用但不影響）for(int j = 0; j < cols; j++) {dfs(0, j, heights, Pmark);}// 2. 標記大西洋的范圍// 右邊界（j=cols-1）的所有格子for(int i = 0; i < rows; i++) {dfs(i, cols-1, heights, Amark);}// 下邊界（i=rows-1）的所有格子for(int j = 0; j < cols; j++) {dfs(rows-1, j, heights, Amark);}// 3. 找兩個范圍的交集for(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {if(Pmark[i][j] && Amark[i][j]) {result.push_back({i, j});}}}return result;}// DFS函數：從(x,y)出發，標記所有能被當前海洋"淹沒"的格子void dfs(int x, int y, vector<vector<int>>& heights, vector<vector<bool>>& mark) {// 1. 如果已經標記過，直接返回（避免重復遞歸）if (mark[x][y]) return;// 2. 標記當前格子為可到達mark[x][y] = true;// 3. 遍歷四個方向，檢查能否逆流而上（往高處漫）for(int i = 0; i < 4; i++) {int nx = x + dx[i]; // 新行坐標int ny = y + dy[i]; // 新列坐標// 邊界檢查：新坐標必須在網格內if(nx >= 0 && ny >= 0 && nx < rows && ny < cols) {// 核心條件：相鄰格子比當前高或相等，且未被標記if (!mark[nx][ny] && heights[nx][ny] >= heights[x][y]) {dfs(nx, ny, heights, mark);}}}}
};

代碼細節解釋：

方向數組：dx 和 dy 定義了上下左右四個方向，避免手寫四次重復代碼。
標記數組：
- Pmark[i][j] = true 表示 (i,j) 的水可以流到太平洋
- Amark[i][j] = true 表示 (i,j) 的水可以流到大西洋
DFS 觸發時機：
- 太平洋從 上邊界（i=0） 和 左邊界（j=0） 開始
- 大西洋從 下邊界（i=rows-1） 和 右邊界（j=cols-1） 開始
- 重復觸發（如 (0,0) 被兩個邊界觸發）不影響，因為 mark[x][y] 會過濾重復
DFS 核心邏輯：
- 先標記當前格子為“可到達”
- 對四個方向的鄰居，只有當 鄰居更高或等高 且 未被標記 時，才遞歸深入
- 這模擬了“水往高處漫”的逆向過程
結果收集：兩個標記數組都為 true 的格子，就是既能流到太平洋又能流到大西洋的目標。

代碼拆解:

1. 類中成員變量解析

class Solution {
public:// 方向數組：上下左右四個方向的坐標偏移，避免重復寫坐標計算int dx[4] = {1, -1, 0, 0};  int dy[4] = {0, 0, 1, -1};  int rows, cols;  // 存儲網格的行數、列數，dfs 中直接復用vector<vector<int>> result;  // 最終結果：同時流向兩大洋的坐標
};

作用：

把重復用的變量（方向、網格尺寸）設為類成員，減少函數傳參，讓代碼更簡潔。
result 集中存結果，避免分散處理。

2. 主函數核心邏輯

vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {// 邊界防護：空網格直接返回if (heights.empty() || heights[0].empty()) return result;  rows = heights.size();  cols = heights[0].size();  // 標記數組：記錄能流向太平洋、大西洋的格子vector<vector<bool>> Pmark(rows, vector<bool>(cols, false));  vector<vector<bool>> Amark(rows, vector<bool>(cols, false));  // 1. 從太平洋邊界啟動 DFS（上邊界 + 左邊界）for (int i = 0; i < rows; i++) dfs(i, 0, heights, Pmark);   // 左邊界for (int j = 0; j < cols; j++) dfs(0, j, heights, Pmark);   // 上邊界  // 2. 從大西洋邊界啟動 DFS（下邊界 + 右邊界）for (int i = 0; i < rows; i++) dfs(i, cols-1, heights, Amark); // 右邊界for (int j = 0; j < cols; j++) dfs(rows-1, j, heights, Amark); // 下邊界  // 3. 找交集：同時被兩個海洋標記的格子for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {if (Pmark[i][j] && Amark[i][j]) {result.push_back({i, j});  }}}return result;
}

核心步驟：

邊界防護：先判空，避免后續越界訪問。
標記數組：Pmark 記能流太平洋的格子，Amark 記能流大西洋的格子。
逆向 DFS：從海洋邊界（太平洋上/左、大西洋下/右）往陸地 “逆流”，標記所有能連通的格子。
找交集：同時被 Pmark 和 Amark 標記的格子，就是答案。

3. DFS 函數核心邏輯

void dfs(int x, int y, vector<vector<int>>& heights, vector<vector<bool>>& mark) {// 已標記過就跳過，避免重復遞歸if (mark[x][y]) return;  mark[x][y] = true;  // 標記當前格子為“可流向對應海洋”// 遍歷四個方向for (int i = 0; i < 4; i++) {  int nx = x + dx[i];  // 新行坐標int ny = y + dy[i];  // 新列坐標// 檢查：新坐標合法 + 未標記 + 高度 >= 當前（逆流條件）if (nx >= 0 && ny >= 0 && nx < rows && ny < cols && !mark[nx][ny] && heights[nx][ny] >= heights[x][y]) {dfs(nx, ny, heights, mark);  // 遞歸標記相鄰格子}}
}

核心設計：

標記優先：進入 DFS 先標記當前格子，避免重復處理。
逆流邏輯：只有相鄰格子高度 >= 當前（模擬 “水往高處漫”），才遞歸（和自然水流相反，是逆向思維關鍵）。
邊界檢查：nx、ny 要在網格內，否則跳過。

4. 局部遞歸示例（以太平洋左邊界 (0,0) 為例）
假設網格如下（簡化示意，僅看關鍵流程）：

heights = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]

觸發 dfs(0, 0, heights, Pmark)（太平洋左邊界起點），遞歸過程：

第一步：dfs(0,0)
- 標記 Pmark[0][0] = true
- 檢查四個方向：
  - 下（dx[0]=1）：nx=1, ny=0 → 高度 4 >= 1 → 遞歸 dfs(1,0)
  - 上、左：越界或已處理，跳過
  - 右：需等待 dfs(1,0) 及其所有遞歸分支執行完畢并回溯后，才會處理 (0,1)。
第二步：dfs(1,0)
- 標記 Pmark[1][0] = true
- 檢查四個方向：
  - 下（nx=2, ny=0）：高度 7 >= 4 → 遞歸 dfs(2,0)
  - 上（nx=0, ny=0）：已標記，跳過
  - 右（nx=1, ny=1）：高度 5 >= 4 → 遞歸 dfs(1,1)
  - 左：越界，跳過
第三步：dfs(2,0)、dfs(1,1) 繼續擴散…
- 最終，所有能從 (0,0) 逆流到達的格子都會被標記為 Pmark = true，模擬 “太平洋的水往陸地漫” 的過程。

遞歸特點：像 “逆向洪水”，從海洋邊界出發，逐步標記所有能連通的陸地，直到無法再逆流為止。

總結
代碼通過 逆向 DFS（從海洋往陸地流） + 雙標記數組（太平洋/大西洋） + 交集篩選，高效解決了 “判斷水流雙向連通” 的問題。類成員變量簡化了傳參，DFS 遞歸實現了 “逆流標記”，主函數通過邊界遍歷 + 交集計算，最終得到結果。

結合示例模擬遞歸流程，能更直觀理解 “逆向思維 + 洪水灌溉” 的巧妙用法～

時間復雜度分析

核心邏輯：算法通過兩次獨立的 DFS 遍歷（分別對應太平洋和大西洋）標記所有可達格子，最終計算交集。
具體計算：
- 網格共有 m*n 個格子（m 為行數，n 為列數）。
- 每個格子最多被 2 次 DFS 訪問（太平洋遍歷一次，大西洋遍歷一次）。
- 每次 DFS 中，每個格子的處理（檢查方向、標記）是常數時間 O(1)。
結論：總時間復雜度為 O(m*n)，與網格規模線性相關，效率高效。

空間復雜度分析

核心消耗：主要來自兩部分——遞歸調用棧和標記數組。
具體計算：
- 標記數組：Pmark 和 Amark 各占用 m*n 空間，合計 O(m*n)。
- 遞歸棧：最壞情況下（如網格是遞增序列，DFS 需遍歷所有格子），遞歸深度可達 m*n（例如從邊界一直遞歸到對角），占用 O(m*n) 空間。
結論：總空間復雜度為 O(m*n)，由標記數組和遞歸棧共同決定。