計算機圖形學編程(使用OpenGL和C++)(第2版) 學習筆記 07.光照

1. 光照

1.1. 光源

光源類型	特點	優點	缺點
環境光	整個場景均勻受光，無方向和位置。	模擬全局光照，避免完全黑暗的區域。	缺乏方向性和真實感，無法產生陰影。
平行光	光線方向平行，無位置，僅有方向。	計算簡單，適合模擬太陽光等遠距離光源。	無法模擬局部光照，缺乏真實感。
點光源	光線從一個點向四周發散，具有位置和方向。	能模擬局部光照，產生陰影和立體感。	計算復雜，光照強度隨距離衰減，性能開銷較大。
聚光燈	光線從一個點沿特定方向發散，形成錐形光照區域。	能模擬手電筒、舞臺燈等聚焦光源，光照區域可控。	計算復雜，需要額外判斷光照角度和范圍。
半球光	模擬天空光照，頂部光線為一種顏色，底部光線為另一種顏色。	能模擬自然光的漸變效果，適合戶外場景。	計算復雜度較高，通常需要結合其他光源使用。
區域光	光線從一個平面或區域發散，具有方向和范圍。	能模擬窗戶、屏幕等光源，光照效果更真實。	計算復雜度高，通常需要光照貼圖或全局光照算法支持。

1.1.1. 環境光

環境光基本原理是，場景中所有方向上都有光，只是強度不同。全局環境光可以定義如下：

float globalAmbient[4] = { 0.6f, 0.6f, 0.6f, 1.0f };

1.1.2. 平行光

平行光的基本原理是，所有的光都從同一個方向照射到物體上，這個方向就是平行光的方向。
平行光無位置，只有方向。它可以用來模擬光源距離非常遠，以至于光線接近平行的情況，例如陽光

指向 z 軸負方向的紅色定向光可以指定如下：

float dirLightAmbient[4] = { 0.1f, 0.0f, 0.0f, 1.0f }; 
float dirLightDiffuse[4] = { 1.0f, 0.0f, 0.0f, 1.0f }; 
float dirLightSpecular[4] = { 1.0f, 0.0f, 0.0f, 1.0f }; 
float dirLightDirection[3] = { 0.0f, 0.0f, -1.0f };

在已經有全局環境光的情況下，定向光的環境光分量看起來似乎是多余的。然而，當光源“開啟”或“關閉”時，全局環境光和定向光的環境光分量的區別就很明顯了。當“開啟”時，總環境光分量將如預期的那樣增加。在上面的例子中，我們只使用了很小的環境光分量。在實際場景中，應當根據場景的需要平衡兩個環境光分量

1.1.3. 點光源

點光源的基本原理是，所有的光都從一個點向各個方向照射到物體上，這個點就是點光源的位置。

1.1.3.1. 點光源的特點

點光源是計算機圖形學和現實照明中常見的一種光源類型，它模擬了從一個點向各個方向均勻發射光線的光源。以下是點光源的主要特點：

1.1.3.1.1. 物理特性方面

位置決定性：點光源有明確的位置坐標，所有光線從該點向四面八方發射。在三維空間中，其位置可以用一個三維向量 (x, y, z) 來精確表示。在場景中移動點光源的位置，會直接改變物體受光的區域和強度分布。
光線發散性：光線從點光源出發，呈輻射狀向周圍空間發散傳播。隨著傳播距離的增加，光線覆蓋的面積會逐漸增大，這符合光的傳播規律。
光照衰減：點光源的光照強度會隨著距離的增加而減弱。根據平方反比定律，光照強度與距離的平方成反比，即距離點光源越遠，物體接收到的光照越弱。

1.1.3.1.2. 渲染效果方面

產生陰影：由于點光源的光線是從一個點發出的，物體被其照射時會在背后產生明顯的陰影。陰影的形狀和范圍取決于物體的形狀、位置以及點光源的位置和強度。
多角度照明：能從多個角度照亮物體，使物體表面產生豐富的明暗變化，增強物體的立體感和層次感。物體朝向點光源的面會被照亮，而背向的面則處于陰影中。
局部照明效果：點光源通常用于突出場景中的特定物體或區域，營造局部照明效果。例如，在游戲場景中，可以用點光源模擬火把、吊燈等，使這些發光物體周圍的環境更加生動。

1.1.3.1.3. 計算復雜度方面

計算量較大：與平行光等簡單光源相比，點光源的光照計算更為復雜。因為需要考慮光源位置、物體與光源的距離、光照衰減等多個因素，所以在實時渲染中，大量使用點光源可能會對性能產生較大影響。
可優化性：為了提高渲染效率，有多種針對點光源的優化算法，如光照探針、光照貼圖等。這些方法可以在一定程度上減少點光源的計算量，同時保持較好的光照效果。

1.1.3.2. 點光源的實現步驟

點光源的實現步驟如下：

計算點光源到物體表面的距離。
計算點光源到物體表面的方向向量。
計算點光源到物體表面的光照強度。
將光照強度應用到物體表面。

點光源具有指定為 RGBA 值的環境光反射、漫反射和鏡面反射特性。
位置(5,2,?3)處的紅色位置光可以指定如下：

float posLightAmbient[4] = { 0.1f, 0.0f, 0.0f, 1.0f }; 
float posLightDiffuse[4] = { 1.0f, 0.0f, 0.0f, 1.0f }; 
float posLightSpecular[4] = { 1.0f,0.0f, 0.0f, 1.0f }; 
float posLightLocation[3] = { 5.0f, 2.0f, -3.0f };
float radius=1.0f;

常見的點光源衰減因子的公式及其特點：

衰減因子公式	名稱	特點	優點	缺點
`attenuation = 1.0`	無衰減	光照強度恒定，不隨距離變化。	計算簡單，適合小范圍光照。	不符合物理規律，無法模擬真實光照效果。
`attenuation = 1.0 / distance`	線性衰減	光照強度與距離成反比。	計算簡單，能模擬一定的衰減效果。	衰減過快，遠距離光照效果較弱。
`attenuation = 1.0 / (distance * distance)`	平方反比衰減	光照強度與距離的平方成反比，符合物理規律。	模擬真實光照效果，適合大范圍光照。	距離較近時光照強度過強，可能導致過曝。
`attenuation = 1.0 / (1.0 + k * distance)`	線性修正衰減	在線性衰減的基礎上加入常數項，避免距離為零時光照強度無限大。	計算簡單，適合實時渲染。	衰減效果可能不夠真實。
`attenuation = 1.0 / (1.0 + k1 * distance + k2 * distance * distance)`	線性+平方修正衰減	綜合線性衰減和平方法，加入常數項，常用于實時渲染。	平衡了近距離和遠距離的光照強度，適合大多數場景。	參數調整較復雜，需要根據場景手動調節 `k1` 和 `k2`。
`attenuation = max(0.0, 1.0 - (distance / radius))`	截斷式衰減	光照強度在一定范圍內線性衰減，超出范圍后強度為零。	適合模擬局部光照，計算簡單。	不符合物理規律，光照范圍外會突然變暗。
`attenuation = exp(-k * distance)`	指數衰減	光照強度隨距離指數級減弱。	模擬柔和的光照衰減效果，適合特定場景。	衰減過快，遠距離光照效果幾乎不可見。
`attenuation = 1.0 / (1.0 + k1 * distance + k2 * distance * distance + k3 * distance^3)`	高階多項式衰減	在線性+平方修正衰減的基礎上加入三次項，模擬更復雜的光照衰減效果。	能模擬更真實的光照效果，適合高質量渲染。	計算復雜度較高，通常用于離線渲染。

線性衰減：

float distance=length(posLightLocation-fragPos);
//float attenuation=1.0/(1.0+radius*distance+radius*radius);
float attenuation=max(0.0,1.0-(distance/radius));
vec3 adjLightColor=lightColor*attenuation;

1.1.4. 聚光燈

聚光燈是一種特殊的光源，它從某個方向照射物體，并在物體表面產生錐形的光照區域。

位于(5,2,?3)向下照射 z 軸負方向的紅色聚光燈可以表示為：

float spotLightAmbient[4] = { 0.1f, 0.0f, 0.0f, 1.0f }; 
float spotLightDiffuse[4] = { 1.0f, 0.0f, 0.0f, 1.0f }; 
float spotLightSpecular[4] = { 1.0f,0.0f, 0.0f, 1.0f }; 
float spotLightLocation[3] = { 5.0f, 2.0f, -3.0f }; 
float spotLightDirection[3] = { 0.0f, 0.0f, -1.0f }; 
float spotLightCutoff = 20.0f; 
float spotLightExponent = 10.0f;

常見的聚光燈衰減因子的公式及其特點：注意：光離軸角必須小于截光角，超過則聚光燈將不會產生光照效果。

衰減因子公式	名稱	特點	優點	缺點
`attenuation = 1.0`	無衰減	光照強度恒定，不隨距離變化。	計算簡單，適合小范圍光照。	不符合物理規律，無法模擬真實光照效果。
`attenuation = 1.0 / distance`	線性衰減	光照強度與距離成反比。	計算簡單，能模擬一定的衰減效果。	衰減過快，遠距離光照效果較弱。
`attenuation = 1.0 / (distance * distance)`	平方反比衰減	光照強度與距離的平方成反比，符合物理規律。	模擬真實光照效果，適合大范圍光照。	距離較近時光照強度過強，可能導致過曝。
`attenuation = 1.0 / (1.0 + k * distance)`	線性修正衰減	在線性衰減的基礎上加入常數項，避免距離為零時光照強度無限大。	計算簡單，適合實時渲染。	衰減效果可能不夠真實。
`attenuation = 1.0 / (1.0 + k1 * distance + k2 * distance * distance)`	線性+平方修正衰減	綜合線性衰減和平方法，加入常數項，常用于實時渲染。	平衡了近距離和遠距離的光照強度，適合大多數場景。	參數調整較復雜，需要根據場景手動調節 `k1` 和 `k2`。
`attenuation = max(0.0, 1.0 - (distance / radius))`	截斷式衰減	光照強度在一定范圍內線性衰減，超出范圍后強度為零。	適合模擬局部光照，計算簡單。	不符合物理規律，光照范圍外會突然變暗。
`attenuation = exp(-k * distance)`	指數衰減	光照強度隨距離指數級減弱。	模擬柔和的光照衰減效果，適合特定場景。	衰減過快，遠距離光照效果幾乎不可見。
`attenuation = cos(theta)`	角度衰減	光照強度與光線方向和片段方向的夾角余弦值成正比。	模擬聚光燈的錐形光照區域，適合手電筒、舞臺燈等場景。	需要額外判斷角度范圍，計算復雜度較高。
`attenuation = pow(cos(theta), exponent)`	指數角度衰減	在角度衰減的基礎上加入指數項，控制光照強度的分布。	能模擬更柔和的聚光燈光照效果，適合高質量渲染。	參數調整復雜，計算復雜度較高。

聚光燈的實現步驟如下：

計算聚光燈到物體表面的距離。
計算聚光燈到物體表面的方向向量。
計算聚光燈到物體表面的光照強度。
計算聚光燈到物體表面的方向向量與聚光燈方向的角度，可以轉換為余弦值。即：cosθ = dot(lightDir,lightDirToFragment)
判斷聚光燈是否能照射到物體上，即cosθ是否大于聚光燈的lightCutoff值（角度<聚光燈的角度）。
將光照強度應用到物體表面。

以下是運行效果：
從中可以看到，聚光燈的光照區域是一個圓形的區域。

1.2. 光照模型

光照模型	特點	優點	缺點
環境光	整個場景均勻受光，無方向和位置。	模擬全局光照，避免完全黑暗的區域。	缺乏方向性和真實感，無法產生陰影。
漫反射光	光線從光源照射到物體表面，光強與光線與表面法線夾角的余弦值成正比。	模擬物體表面的基本光照效果，增強立體感。	無法模擬高光效果，缺乏真實感。
鏡面反射光	光線從光源照射到物體表面后，沿特定方向反射，產生高光效果。	模擬光滑表面的高光效果，增強真實感。	計算復雜度較高，依賴視角位置。
Phong 光照模型	結合環境光、漫反射光和鏡面反射光，模擬物體表面的綜合光照效果。	光照效果較為真實，適合大多數場景。	計算復雜度較高，性能開銷較大。
Blinn-Phong 光照模型	Phong 模型的優化版本，使用半程向量計算鏡面反射光。	性能較高，適合實時渲染。	高光效果可能不如 Phong 模型精確。
Cook-Torrance 光照模型	基于物理的光照模型，考慮微表面結構和 Fresnel 效應。	光照效果非常真實，適合高質量渲染。	計算復雜度極高，通常用于離線渲染。
Toon 光照模型	非真實感光照模型，使用離散的光照強度模擬卡通風格。	模擬卡通風格，適合特定藝術風格的場景。	不適合真實感場景，光照效果較為簡單。
Oren-Nayar 光照模型	模擬粗糙表面的漫反射光，考慮表面微結構的影響。	更真實地模擬粗糙表面的光照效果。	計算復雜度較高，性能開銷較大。
Minnaert 光照模型	模擬暗表面或背光場景的光照效果，光強與視角和光源方向相關。	適合模擬月球表面等特殊場景的光照效果。	不適合一般場景，光照效果較為特殊。

1.3. 材質

每個物體都有其獨特的材質，材質決定了物體對光的各種特性。通黨我們用四個參數：環境光反射、漫反射、鏡面反射、光澤來描述材質。要模擬錫鉛合金的效果，可以指定如下值：

float pewterMatAmbient[4] = { .11f, .06f, .11f, 1.0f }; 
float pewterMatDiffuse[4] = { .43f, .47f, .54f, 1.0f }; 
float pewterMatSpecular[4] = { .33f, .33f, .52f, 1.0f }; 
float pewterMatShininess = 9.85f;

1.4. Phong光照

這是一個運行效果：

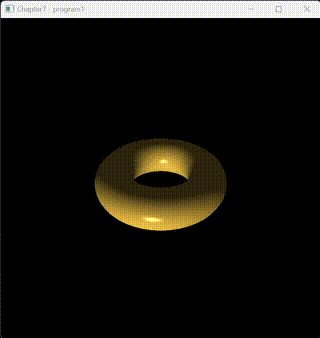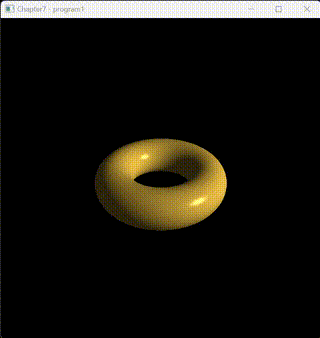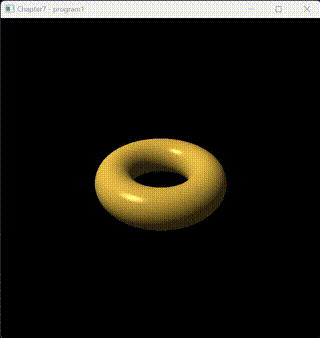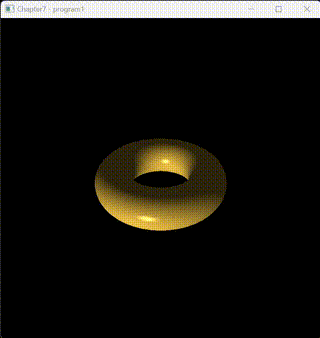
Phong光照模型是一種經典的光照模型，用于模擬真實世界中的光照效果，它將光照分為環境光（Ambient）、漫反射光（Diffuse）和鏡面反射光（Specular）三個部分。最終的光照顏色是這三部分光照顏色的總和。

Phong Reflection Model 來自維基百科上的數據

下面詳細介紹各部分的數學公式及整體公式。

1.4.1. 環境光（Ambient）

環境光模擬了場景中全局的、均勻的光照，它不依賴于光源的位置和物體的朝向。環境光的計算公式如下：
$I_{ambient} = k_a \times I_a \times M_a$
其中：

$I_{ambient}$ 是環境光的顏色強度。
$k_a$ 是物體的環境光反射系數，取值范圍通常在 $[0, 1]$ 之間，它表示物體對環境光的反射能力。
$I_a$ 是環境光的顏色強度。
$M_a$ 是材質的環境光顏色強度。

1.4.2. 漫反射光（Diffuse）

漫反射光模擬了光線在物體表面的均勻散射，它取決于光線的方向和物體表面法線的夾角。漫反射光的計算公式基于 Lambert 余弦定律：
$I_{diffuse} = k_d \times I_d \times M_d \times \max(0, \mathbf{N} \cdot \mathbf{L})$
其中：

$I_{diffuse}$ 是漫反射光的顏色強度。
$k_d$ 是物體的漫反射系數，取值范圍通常在 $[0, 1]$ 之間，它表示物體對漫反射光的反射能力。
$I_d$ 是光源的顏色強度。
$M_d$ 是材質的漫反射顏色強度。
$\mathbf{N}$ 是物體表面的法線向量，且為單位向量。
$\mathbf{L}$ 是從物體表面指向光源的單位向量。
$\mathbf{N} \cdot \mathbf{L}$ 是 $\mathbf{N}$ 和 $\mathbf{L}$ 的點積， $\max(0, \mathbf{N} \cdot \mathbf{L})$ 確保結果不會為負數。

1.4.3. 鏡面反射光（Specular）

鏡面反射光模擬了光線在物體表面的鏡面反射效果，它取決于觀察者的位置。鏡面反射光的計算公式如下：
$I_{specular} = k_s \times I_s \times M_s \times (\max(0, \mathbf{R} \cdot \mathbf{V}))^n$
其中：

$I_{specular}$ 是鏡面反射光的顏色強度。
$k_s$ 是物體的鏡面反射系數，取值范圍通常在 $[0, 1]$ 之間，它表示物體對鏡面反射光的反射能力。
$I_s$ 是光源的顏色強度。
$M_s$ 是材質的反射光顏色強度。
$\mathbf{R}$ 是反射光線的單位向量，可以通過公式 $\mathbf{R} = 2(\mathbf{N} \cdot \mathbf{L})\mathbf{N} - \mathbf{L}$ 計算得到。GLSL 中采用函數reflect()來計算。
$\mathbf{V}$ 是從物體表面指向觀察者的單位向量。
$n$ 是高光指數（Shininess），它控制了鏡面反射的范圍，值越大，高光越集中。

以余弦指數建模的反光度

1.4.3.1. Phong光照模型整體公式

最終的光照顏色 $I_{total}$ 是環境光、漫反射光和鏡面反射光的總和：
$I_{total} = I_{ambient} + I_{diffuse} + I_{specular}$
將前面的公式代入可得：
$I_{total} = k_a \times I_a \times M_a + k_d \times I_d \times M_d \times \max(0, \mathbf{N} \cdot \mathbf{L}) + k_s \times I_s \times M_s \times (\max(0, \mathbf{R} \cdot \mathbf{V}))^n$
上述是一個非常簡單的 Phong 光照模型，它只考慮了環境光、漫反射光和鏡面反射光三個部分，且漫反射光和鏡面反射光均只有一個光源。
如果是有多個光源，則需要分別計算每個光源對物體的光照貢獻，然后將它們相加得到最終的光照顏色。

代碼之間的簡要邏輯關系如下：

法線矩陣（Normal Matrix）是用于將法線向量從模型空間（Model Space）變換到世界空間（World Space）的矩陣。
由于法線向量表示的是表面的方向，它的變換規則和普通的位置向量有所不同。當模型矩陣包含非均勻縮放時，直接使用模型矩陣變換法線向量會導致法線方向錯誤，因此需要使用法線矩陣來確保法線向量在變換后仍然垂直于物體表面。
法線矩陣是模型矩陣的逆轉置矩陣的左上角 3x3 子矩陣。數學表達式如下：
$M_{normal} = (M_{model}^{-1})^T ]$

可以使用 glm 庫中的函數來計算法線矩陣。以下是一個示例代碼：

mat3 normalMatrix = transpose(inverse(mat3(model)));

在實際應用中，特別是在使用4x4矩陣處理變換（如模型視圖矩陣或模型視圖投影矩陣）的情況下，有時會將3x3的法線矩陣擴展為4x4矩陣以適應現有的數學庫或者為了與位置變換統一起來處理。這種情況下，通常是將3x3的法線矩陣放在4x4矩陣的左上角，并將第四行和第四列設置為(0, 0, 0, 1)。但請注意，這樣做主要是出于方便的考慮，實際上只有左上角的3x3部分對法線向量的變換有效。

從頂點著色器到片段著色器的向量，因為涉及到插值，可以不是單位向量，所以在片段著色器中使用前需要歸一化

Blinn-Phong 光照模型

Blinn-Phong 光照模型是 Phong 光照模型的一個優化版本，它使用半程向量（Halfway Vector）來計算鏡面反射光，從而減少了計算量。半程向量是光線和視線之間的中點，它與視線方向和光線方向都垂直。
Blinn 發現向量 R 在計算過程中并不是必需的——R 只是用來計算角 φ 的手段。角 φ 的計算
可以不使用向量 R，而通過 L 與 V 的角平分線向量 H 得到。如圖 7.13 所示，H 和 N 之間的角 α
剛好等于 1/2(φ)。雖然 α 與 φ 不同，但 Blinn 展示了使用 α 代替 φ 就已經可以獲得足夠好的結果。
角平分線向量可以簡單地使用 L+V 得到（見圖 7.14）