前言:
本章節代碼均在Gitee中開源:
衛星位置計算代碼![]() https://gitee.com/Ehundred/navigation-engineering/tree/master/%E5%8D%AB%E6%98%9F%E5%AF%BC%E8%88%AA%E5%8E%9F%E7%90%86/GPS%E5%8D%AB%E6%98%9F%E4%BD%8D%E7%BD%AE%E8%A7%A3%E7%AE%97/Satellite_position_calculation其中涉及到時空轉換的部分,在另一章節有詳細講解,如有疑惑可以先閱讀上一章節:
https://gitee.com/Ehundred/navigation-engineering/tree/master/%E5%8D%AB%E6%98%9F%E5%AF%BC%E8%88%AA%E5%8E%9F%E7%90%86/GPS%E5%8D%AB%E6%98%9F%E4%BD%8D%E7%BD%AE%E8%A7%A3%E7%AE%97/Satellite_position_calculation其中涉及到時空轉換的部分,在另一章節有詳細講解,如有疑惑可以先閱讀上一章節:
時空坐標轉換![]() https://blog.csdn.net/qq_74260823/article/details/139271746?spm=1001.2014.3001.5501
https://blog.csdn.net/qq_74260823/article/details/139271746?spm=1001.2014.3001.5501
因為這章是學校作業,所以稍微正經點.?
衛星參數的讀取
首先,關于導航電文的理解和構成,如果還不太了解,請移步另一篇文章:
衛星信號的構成![]() http://t.csdnimg.cn/6yY29
http://t.csdnimg.cn/6yY29
導航電文會發出很多參數,最終會被接收機接收到,然后轉換為人類可以看懂的具體的數字。接收機在轉換之后,會把適用于我們定位的數據單獨列出來,然后寫入文件之中成為廣播星歷,其中文件的格式長這樣:
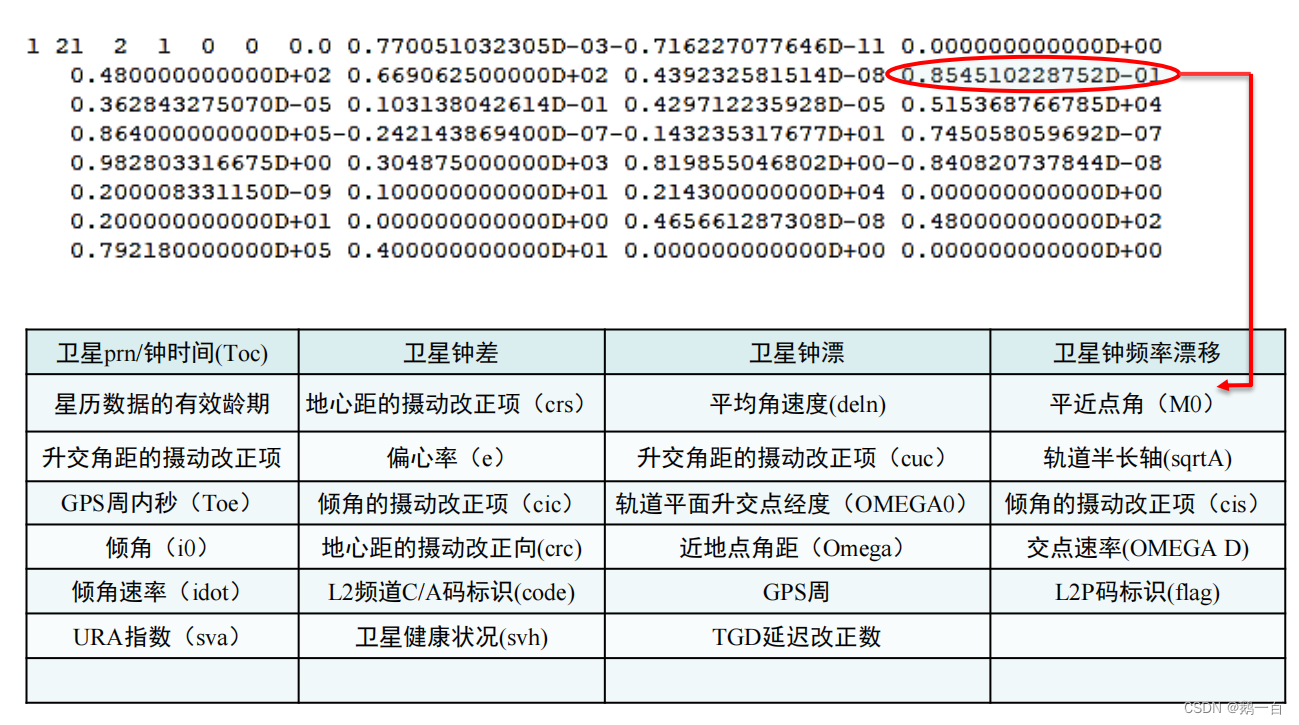 其具體對應的含義是:
其具體對應的含義是:

因為寫入的格式一定是固定的,所以我們讀取數據的時候,也可以利用這些固定的格式,按順序定義一個結構體:
struct satellite_data_block
{double Serial;//序列號double year;double month;double day;double hour;double minute;double second;//年月日時分秒double a0;//衛星鐘差double a1;//衛星鐘偏double a2;//衛星鐘偏移double AODE;//數據齡期double Crs;//軌道半徑改正項double deltan;//平均角速度改正項double M0;//平近點角double Cuc;//升交點角距改正項double e;//軌道偏心率double Cus;//升交點角距改正項double sqrtA;//軌道長半軸平方根double TOE;//星歷的參考時刻 周內秒double Cic;//軌道傾角的改正項double OMEGA;//升交點經度double Cis;//軌道傾角改正項double i0;//軌道傾角double Crc;//軌道半徑的改正項double omega;//近地點角距double deltaomega;//升交點赤經變化double IDOT;//軌道傾角的變率//對于單點定位,以上數據足以,但是為了保持衛星數據完整,以下保持了所有的數據double CA;//CA碼double GPSweek;//gps周數double L2P;//L2P碼double SVA;//衛星精度double SVH;//衛星健康double TGD;//電離層延遲double IODC;//數據質量double shoot_time;//發射時間double h;//擬合區間
};為什么序列號,年月日時分秒也要用double,在待會會講解。?
而讀取的時候,因為格式是固定的,每一個完整的數據都有8行,我們可以每次就讀8行,然后把這8行合并成同一個字符串,用來表示同一個數據塊。而這個函數只負責讀取,把讀取的數據轉換為可用的數據并導入在結構體中,就交給另外一個函數來完成。
void read()
{fstream ifs(_path_name, ios_base::in);if (!ifs) exit(-1);while (!ifs.eof()){string data;for (int i = 0; i < 8; i++){//采用的是讀取整個數據塊的方法char buffer[82];ifs.getline(buffer, 81);data += buffer;}get_data(data);}
}這個把字符串轉換成有用的數據的方法,可以有很多實現形式,完全憑個人習慣。因為有36個數據,我們就定義一個36大小的double數組,每次讀一個數據,就把數據放在double數組之中,一直到讀完整個36個數據。
而讀完之后,因為結構體采用的是內存連續區間,而數組也是內存連續區間,我們之間用memcpy,把數組的內存copy到結構體的內存上,就省略了大量的代碼量。
void get_data(string& data)
{double init[36];int cur = 0;for (int i = 0; i < 36; i++){string tmp = get_part(data, cur);//獲取一串數字的字符串init[i] = _to_double(tmp);//把獲得的字符串轉換成double//兩個函數的具體實現看個人習慣,我的實現可以去看完整代碼}satellite_data_block ins;memcpy(&ins, init, sizeof(double) * 36);_serial.insert(make_pair(ins.Serial, _data.size()));_data.push_back(ins);
}讀取之后,我們直接把他放在數組中,然后接著讀取下一個。最終數組中便完整記錄了所有衛星的參數,我們可以訪問任意衛星的參數。
但是,這里會有一個問題:我們怎么知道數組中對應的是哪個衛星?難道第5個元素對應的一定是序號為5的衛星嗎?當然不一定。我們有兩個解決方案:
- 每次遍歷數組,查看每個元素的序列號
- 用哈希表,把元素下標對應上衛星的序列號
第一個方法的時間復雜度每次都是O(n),自然是比較不靠譜的,所以我們就采用了第二個方法,用哈希表的搜索降低時間復雜度。
衛星位置的解算
導航電文是兩個小時更新一次的。因為這個特性,注定了導航電文無法發送即時的位置數據,所以衛星只能發送更新時刻的位置,然后根據一些參數來模擬衛星的運動,推算出衛星每一刻的位置。
用最簡單的思想來看待這個問題,其實也很簡單:
只不過具體實現的時候,要考慮的影響因素有很多就是了。
因為每個衛星參數對應的位置是獨立的,所以對每一個衛星參數,我們都用一個類來表示,類中包含所有可能要用到的參數:
class calculate
{
private:double sqrtA;double angular_velocity;double _tk;double _angular_velocity;double _Mk;double _Ek;double _Vk;double _argument_of_latitude;double _Cuk;double _Crk;double _Cik;double _Uk;double _Rk;double _Ik;double _OMGk;
};具體的符號會在計算的過程中講解。?
1.計算角速度

第一個在廣播星歷中已經給出,我們只需要計算第二個:
#define GM 3.9860050E14void sqrt_A(double sqrt_a)
{sqrtA = sqrt_a;angular_velocity = sqrt(GM) / pow(sqrtA, 3);
}2.計算衛星運動時間

因為廣播星歷給出的時間Toe是每次更新的瞬間時間,而Tobs是當前的觀測時間,所以Tobs-Toe,再消去衛星信號傳播時間導致的誤差,就是衛星運動的時間Tk。
注意:在廣播星歷中,給出的Toe是周內秒,而實際的計算計算的是總時間差。這里的Toe并非表示周內秒,而是GPS包含周的總時間。為了計算方便,我們可以直接把他轉換成Unix時來進行加減。
double get_time(double Toe,double week,atime cur = curtime)
{//因為沒有考慮信號傳播時間,最終有小部分誤差GPStime _bt(week, Toe);atime bt(_bt);double ret = cur.GetGtime()._time-bt.GetGtime()._time;if (ret > ROUND_SECOND/2) ret -= ROUND_SECOND;else if (ret < -ROUND_SECOND / 2) ret += ROUND_SECOND;//ROUND_SECOND GPS周一周的秒數_tk = ret;return ret;
}3.對平均角速度改正

在廣播星歷中,會給出一個參數:Δn,這個參數就是給我們用以修正角速度的,我們直接把計算出的角速度修正上Δn便可以了:
double new_angular_velocity(double deltan)
{_angular_velocity = angular_velocity + deltan;return _angular_velocity;
}4.計算平近點角
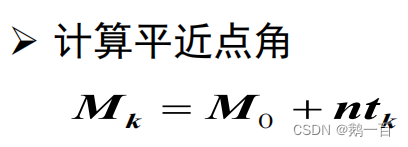
廣播星歷會給出一個參數M0,是在數據更新時刻的近點角。而此時,衛星運動了Tk時刻,我們用角速度n乘以運動時間Tk,就能得出衛星距離更新時刻轉動的角度,再加上更新時刻的角度,就是當前時刻的平近點角
double mean_anomaly(double M0)
{_Mk = M0 + _tk * _angular_velocity;return _Mk;
}?5.計算偏近點角
公式:
和時空轉換一樣,我們發現,這個公式左邊有一個E,右邊有一個E,怎么可以用自己來計算自己呢?這里就要用迭代的方法,取E一個初值En,然后不斷求下一個自己的值En+1,一直到En+1和En相差很小很小,就代表他們收斂到了一個具體的值上,這個值就是我們要求得的值。?

double Eccentric_Anomaly(double e)
{double Mk = _Mk;auto get_Ek = [e,Mk](double Ep){return Ep - (Ep - e * sin(Ep) - Mk) / (1 - e * cos(Ep));};double E0 = _Mk;double E1 = get_Ek(E0);while (abs(E1 - E0) >= 1E-14){E0 = E1;E1 = get_Ek(E0);}_Ek = E1;return _Ek;
}6.計算真近點角
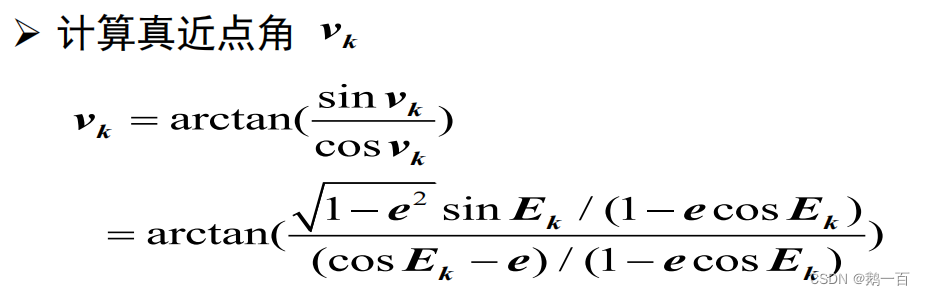
double True_anomaly(double e)
{_Vk = atan((sqrt(1 - e * e) * sin(_Ek) )/ (cos(_Ek) - e));if (abs(_Vk - _Mk) > Pi / 2)_Vk += _Vk > _Mk ? -Pi : Pi;return _Vk;
}?這里也可以直接用atan2來實現。
有一點要注意:導航電文中給出的所有數據都是弧度,而非角度,所以我們在使用sin等函數的時候,直接使用廣播星歷中的數據便可以了,不需要角度轉弧度即*180/Pi
7.計算升交角距

double argument_of_latitude(double omega)
{_argument_of_latitude = _Vk + omega;return _argument_of_latitude;
}8.計算二階調和改正數

double Correction_of_uk(double cuc,double cus)
{_Cuk = cus * sin(2 * _argument_of_latitude) + cuc * cos(2 * _argument_of_latitude);return _Cuk;
}double Correction_of_rk(double crc, double crs)
{_Crk = crs * sin(2 * _argument_of_latitude) + crc * cos(2 * _argument_of_latitude);return _Crk;
}double Correction_of_ik(double cic, double cis)
{_Cik = cis * sin(2 * _argument_of_latitude) + cic * cos(2 * _argument_of_latitude);return _Cik;
}9.計算改正后的開普勒軌道根數


double get_uk()
{_Uk = _argument_of_latitude + _Cuk;return _Uk;
}double get_rk(double e)
{_Rk = sqrtA*sqrtA * (1 - e * cos(_Ek)) + _Crk;return _Rk;
}double get_ik(double i0, double idot)
{_Ik = i0 + _Cik + idot * _tk;return _Ik;
}double get_OMGk(double OMG0,double OMGd,double toe)
{_OMGk = OMG0 + (OMGd - OMGE) * _tk - OMGE * toe;return _OMGk;
}?10.計算衛星的位置
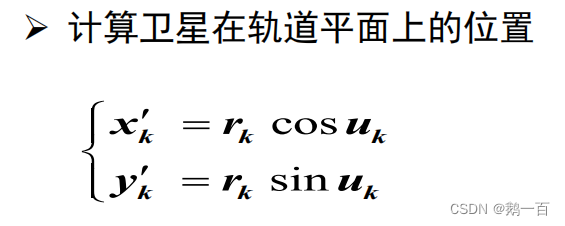

在求出衛星在軌道平面坐標系的坐標后,把該坐標繞x軸旋轉i角(軌道傾角),繞z軸旋轉OmegaK角(升交點經度),得到的便是在地心地固坐標系下的坐標。這個部分是線代中的坐標系轉換,具體的方程感興趣可以自己推導
vector<double> get_xyz()
{double _xk = _Rk * cos(_Uk);double _yk = _Rk * sin(_Uk);double x = _xk * cos(_OMGk) - _yk * cos(_Ik) * sin(_OMGk);double y = _xk * sin(_OMGk) + _yk * cos(_Ik) * cos(_OMGk);double z = _yk * sin(_Ik);return { x,y,z };
}最終,便可以得到衛星坐標的位置xyz。
代碼匯總:
我們采用了一個類來完成,在傳入一個衛星數據塊后,便在構造函數里直接計算出該數據塊對應的衛星位置。而因為讀取衛星數據,計算衛星數據是分離的,所以我們可以再設計另外一個接口,將兩個類的功能結合在一起,而這個實現方法可以根據個人習慣,也可以直接參考我完整的代碼。
#define GM 3.9860050E14
#define OMGE 7.2921151467E-5commontime _curtime = commontime({ 2021,2,1,0,0 }, 30);//當前觀測時間
atime curtime = atime(_curtime);//計算的完整過程,必須按順序依次進行
class calculate
{
public:vector<double> _calculate(const satellite_data_block& s){sqrt_A(s.sqrtA);get_time(s.TOE, s.GPSweek);new_angular_velocity(s.deltan);mean_anomaly(s.M0);Eccentric_Anomaly(s.e);True_anomaly(s.e);argument_of_latitude(s.omega);Correction_of_uk(s.Cuc, s.Cus);Correction_of_rk(s.Crc, s.Crs);Correction_of_ik(s.Cic, s.Cis);get_uk();get_rk(s.e);get_ik(s.i0, s.IDOT);get_OMGk(s.OMEGA, s.deltaomega, s.TOE);vector<double> xyz = get_xyz();return xyz;}
private:void sqrt_A(double sqrt_a){sqrtA = sqrt_a;angular_velocity = sqrt(GM) / pow(sqrtA, 3);}double get_time(double Toe,double week,atime cur = curtime){//因為沒有考慮信號傳播時間,最終有小部分誤差GPStime _bt(week, Toe);atime bt(_bt);double ret = cur.GetGtime()._time-bt.GetGtime()._time;if (ret > ROUND_SECOND/2) ret -= ROUND_SECOND;else if (ret < -ROUND_SECOND / 2) ret += ROUND_SECOND;_tk = ret;return ret;}double new_angular_velocity(double deltan){_angular_velocity = angular_velocity + deltan;return _angular_velocity;}double mean_anomaly(double M0){_Mk = M0 + _tk * _angular_velocity;return _Mk;}double Eccentric_Anomaly(double e){double Mk = _Mk;auto get_Ek = [e,Mk](double Ep){return Ep - (Ep - e * sin(Ep) - Mk) / (1 - e * cos(Ep));};double E0 = _Mk;double E1 = get_Ek(E0);while (abs(E1 - E0) >= 1E-14){E0 = E1;E1 = get_Ek(E0);}_Ek = E1;return _Ek;}double True_anomaly(double e){_Vk = atan((sqrt(1 - e * e) * sin(_Ek) )/ (cos(_Ek) - e));if (abs(_Vk - _Mk) > Pi / 2)_Vk += _Vk > _Mk ? -Pi : Pi;return _Vk;}double argument_of_latitude(double omega){_argument_of_latitude = _Vk + omega;return _argument_of_latitude;}double Correction_of_uk(double cuc,double cus){_Cuk = cus * sin(2 * _argument_of_latitude) + cuc * cos(2 * _argument_of_latitude);return _Cuk;}double Correction_of_rk(double crc, double crs){_Crk = crs * sin(2 * _argument_of_latitude) + crc * cos(2 * _argument_of_latitude);return _Crk;}double Correction_of_ik(double cic, double cis){_Cik = cis * sin(2 * _argument_of_latitude) + cic * cos(2 * _argument_of_latitude);return _Cik;}double get_uk(){_Uk = _argument_of_latitude + _Cuk;return _Uk;}double get_rk(double e){_Rk = sqrtA*sqrtA * (1 - e * cos(_Ek)) + _Crk;return _Rk;}double get_ik(double i0, double idot){_Ik = i0 + _Cik + idot * _tk;return _Ik;}double get_OMGk(double OMG0,double OMGd,double toe){_OMGk = OMG0 + (OMGd - OMGE) * _tk - OMGE * toe;return _OMGk;}vector<double> get_xyz(){double _xk = _Rk * cos(_Uk);double _yk = _Rk * sin(_Uk);double x = _xk * cos(_OMGk) - _yk * cos(_Ik) * sin(_OMGk);double y = _xk * sin(_OMGk) + _yk * cos(_Ik) * cos(_OMGk);double z = _yk * sin(_Ik);return { x,y,z };}private:double sqrtA;double angular_velocity;double _tk;double _angular_velocity;double _Mk;double _Ek;double _Vk;double _argument_of_latitude;double _Cuk;double _Crk;double _Cik;double _Uk;double _Rk;double _Ik;double _OMGk;
};
調試數據:
為了方便大家調試,我列出了對應的調試數據:
對應我的文件中序列號為1的衛星:
廣播星歷參數:
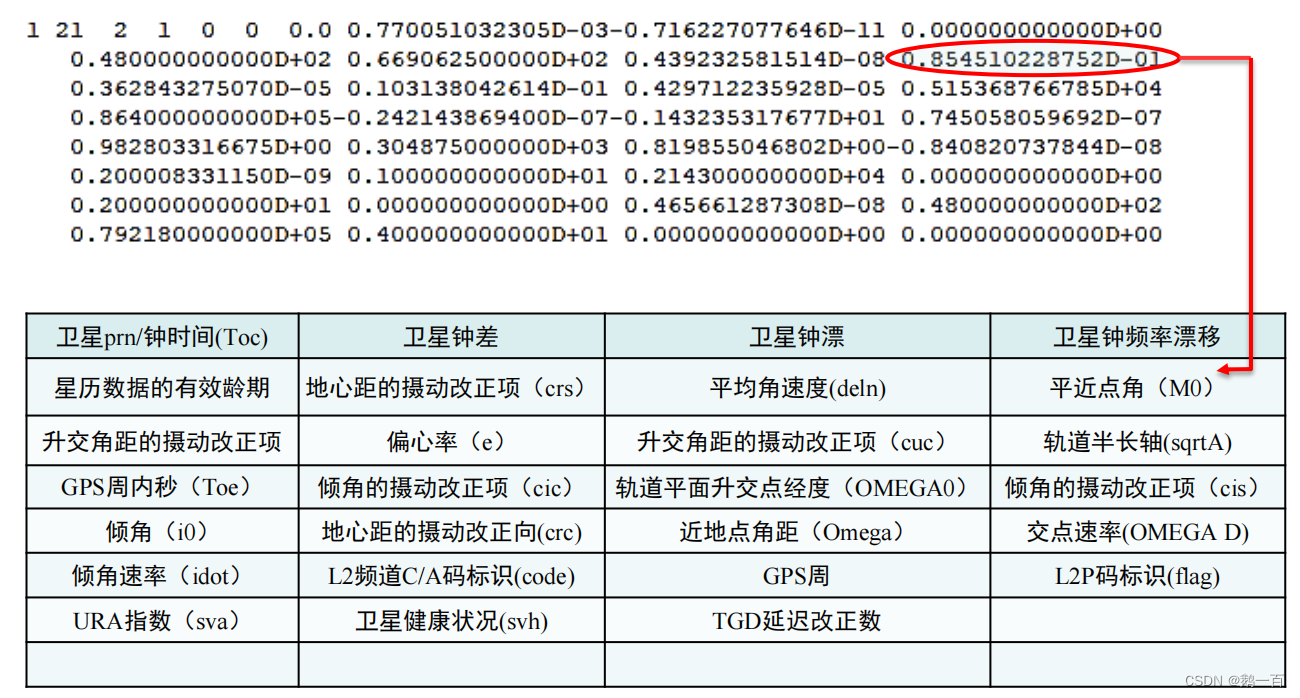
計算出的數據: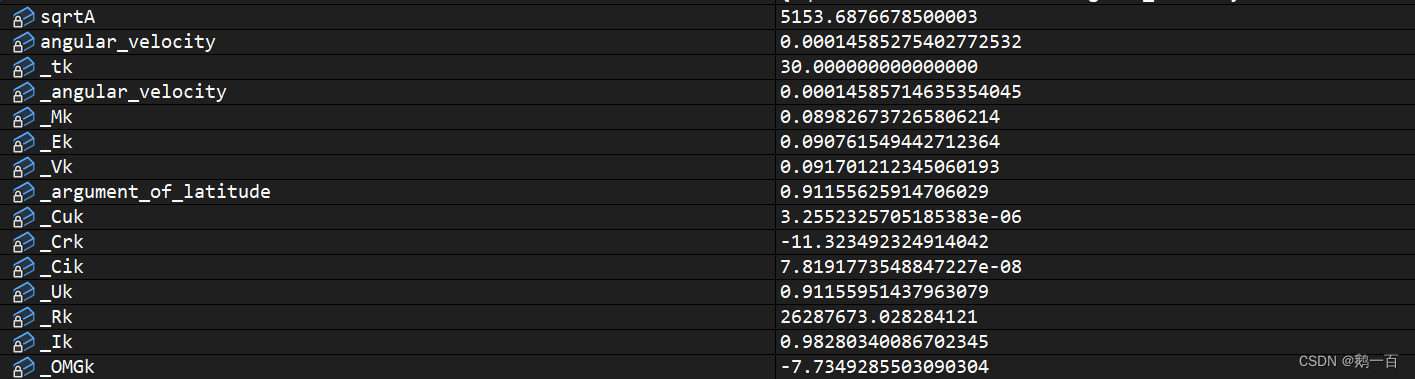 最終結果:
最終結果: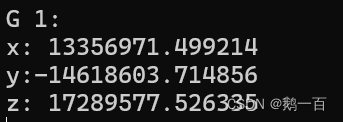
更多的測試用例可以直接在完整源碼中查看所有31個衛星數據?
最后,給自己疊個甲。因為自己才是導航工程大二的本科生,有些概念理解可能不到位,而又想用最容易理解的方式表達出來,所以可能正確性會稍微有些偏差。但是對初學者來說,應該不會存在太大的錯誤,如果可以幫到你,真的榮幸之極。還有



)

![[C/C++]_[初級]_[在Windows和macOS平臺上導出動態庫的一些思考]](http://pic.xiahunao.cn/[C/C++]_[初級]_[在Windows和macOS平臺上導出動態庫的一些思考])



)

】技巧)








