還記得什么是光柵化咩？

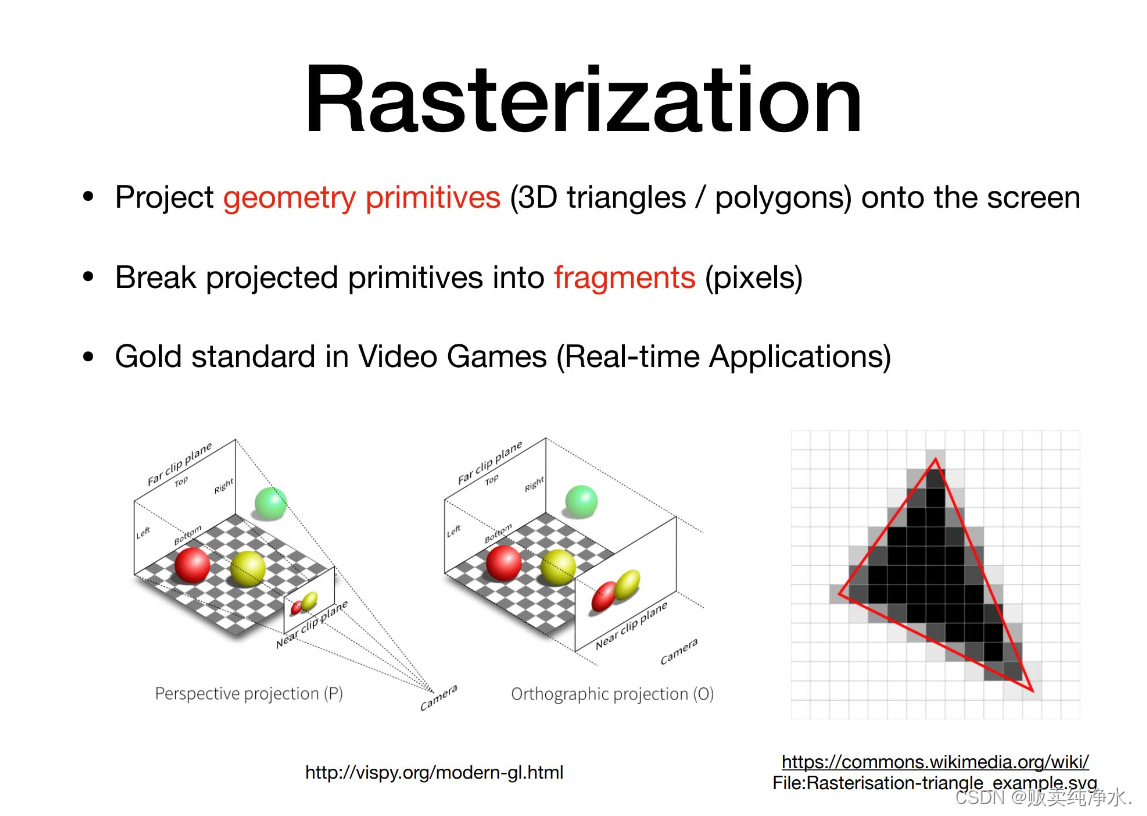
將三維空間的幾何形體顯現在屏幕上，這就是光柵化（游戲、實時圖形學的應用）

Perspective Projection

在正交投影里如何定義三維空間中的立方體呢？

用x軸的覆蓋（左、右），y軸的覆蓋（上、下），z軸的覆蓋（遠、近）

遠近用正交投影和透視投影都是一樣的，在做透視投影的時候，是需要把視錐變成長方體

那我們如何定義這樣一個視錐呢？

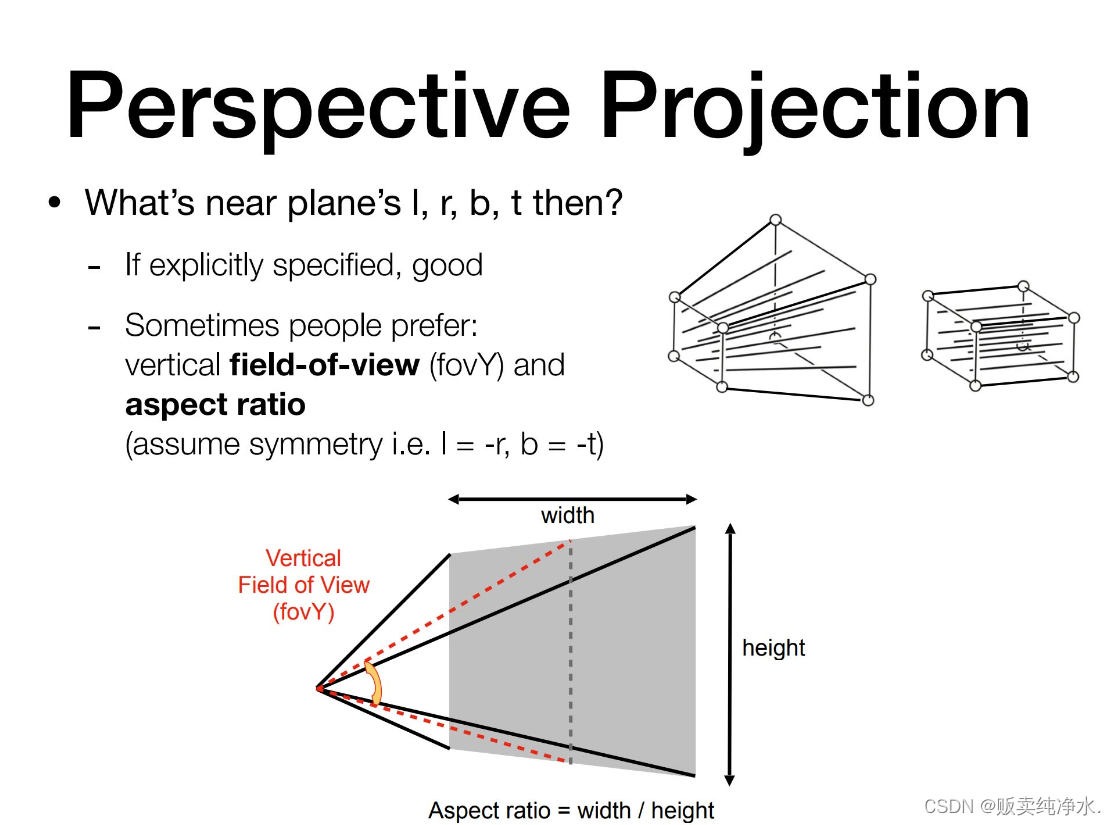
從攝像機出發，看向某一個區域，看到的近平面為其定義寬度和高度，就像是看顯示器一樣，定義一個寬高比，那什么是寬高比呢？

寬高比，顧名思義，它的寬度除以它的高度，即視圖區域可看到的長寬比

我們還需要一個定義：視角（可看到的角度的范圍，垂直可視角度，廣角就是指垂直可視角度較大）

由長寬比和垂直可視角度可以推出水平可視角度

把攝像機擺放到某各個位置，向一個方向看，如果從側面看可以看到這樣的三角形，右面的線和攝像機距離是，我們已知垂直可視角度，可視角度是上下兩條連線的夾角，垂直可視角度/2是三角形張開的角度，可得出兩個公式：

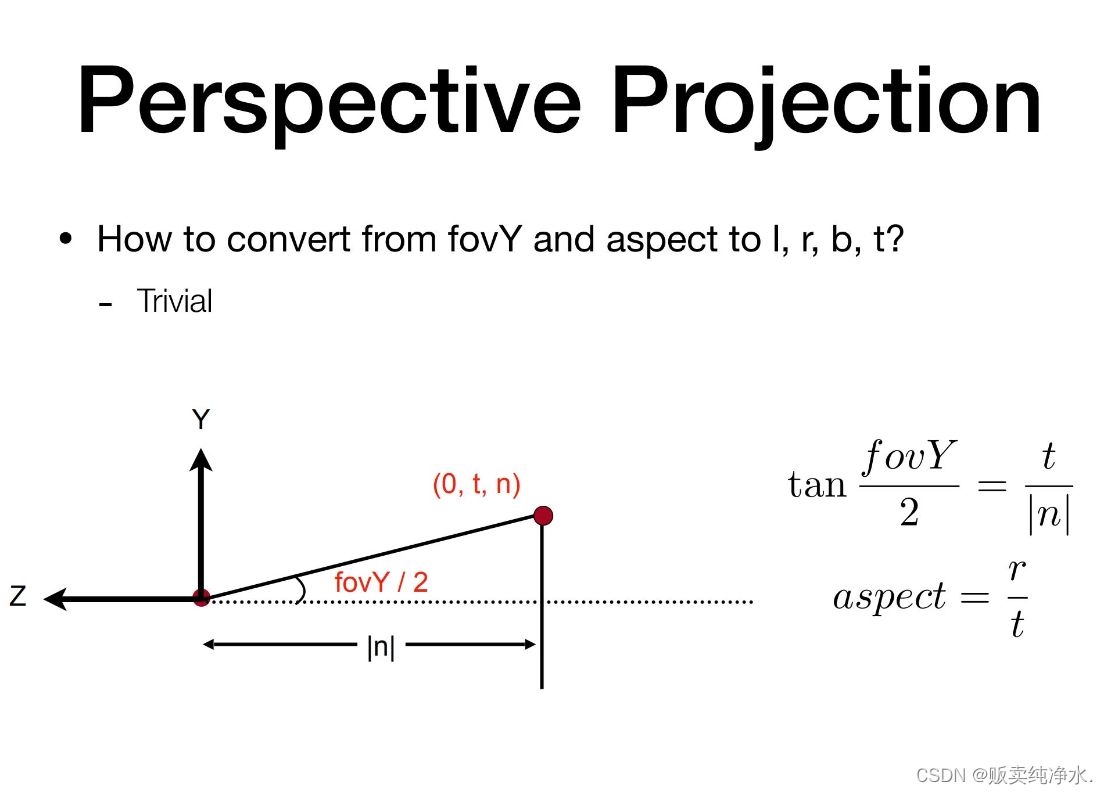
定義視錐：定義垂直可視角度、定義寬高比?

可以自動轉化到定義正交投影的遠近、左右、上下

根據前置內容，所有東西都可以轉化到這樣一個立方體上：

我們如何將這個立方體畫到屏幕上呢？

既然要畫到屏幕上那就先明確屏幕的定義，在計算機圖形學中，屏幕被定義成一個二維的數組，數組中的每一個元素被定義成一個像素，像素的多少可以組成分辨率的概念

屏幕是典型的光柵成像設備，光柵即屏幕，把東西畫在屏幕上就是光柵化的過程

像素：picture element（居然真的是像素。。。），像素是最小的單位，在里面不會有變化

透視投影轉化成正交投影需要保證近和遠兩個平面是不變的，大小是近遠兩平面都會變得和近平面一樣大

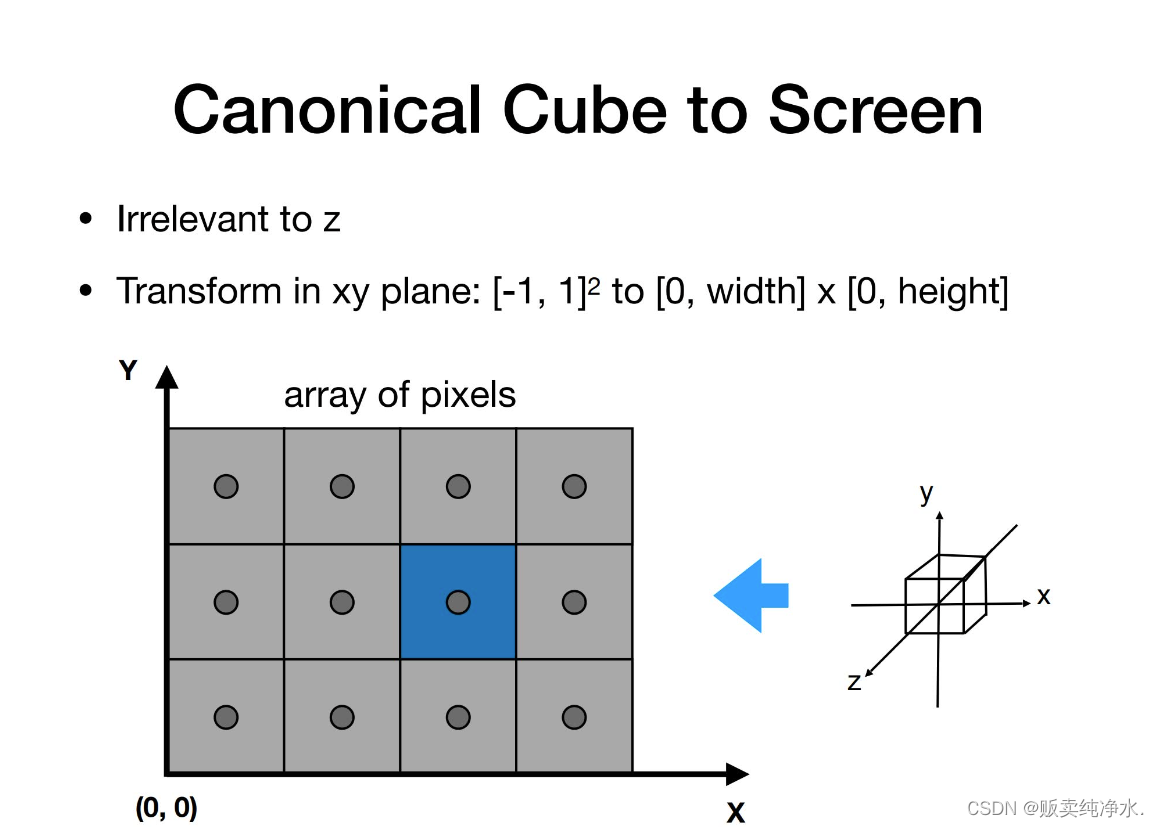
Canonical Cube to Screen

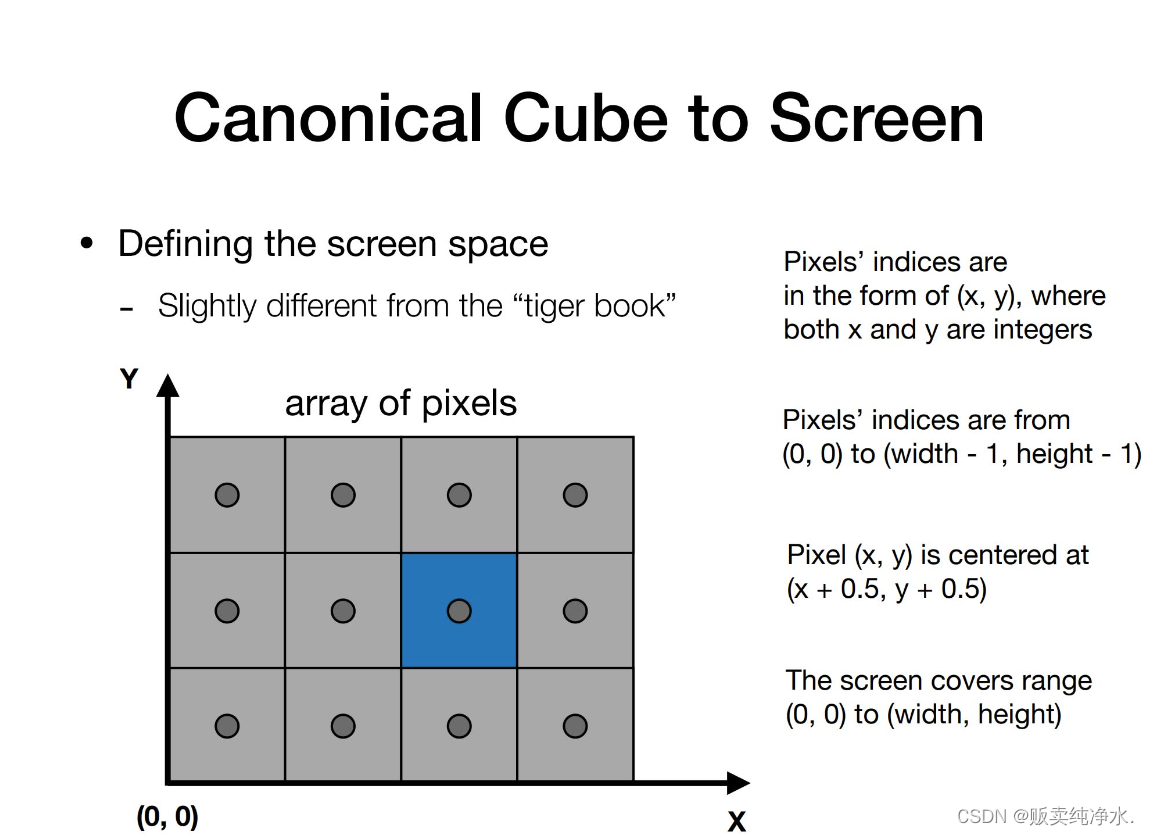
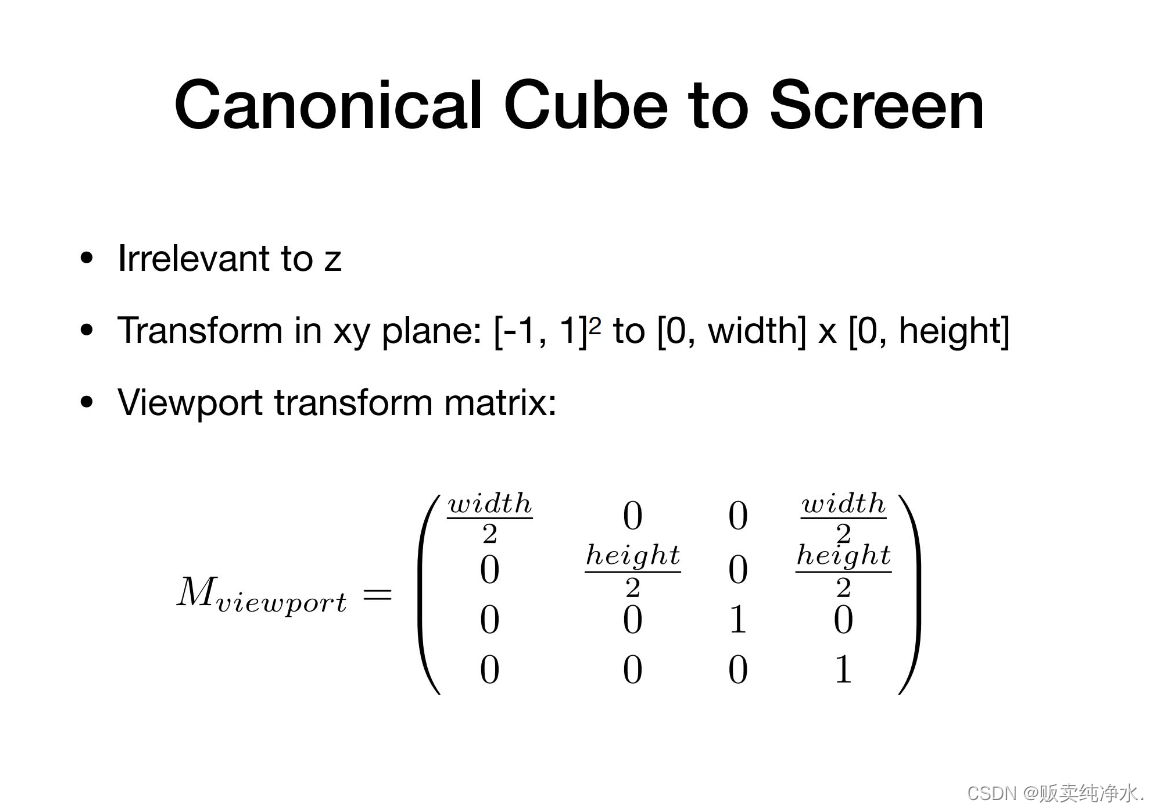
?定義像素坐標，均寫成形式，用整數坐標描述，比如現在的藍色像素可以用表示（從0開始數），屏幕的分辨率從開始一直到，像素的中心是，從三維空間到屏幕變換（立方體映射到屏幕空間）：

有z怎么辦呢？?

z先不用管，后面有它的用途，至于x和y，將這個拉成寬度是width，高度是height，因為-1~1是2，所以需要先/2再×對應的高度或者寬度，我們要把屏幕空間的左下角定義到原點上，也就是說原來的中心是那需要把它移到該在的位置上，這個變換被稱為視口變換

?下一步我們要把空間中描述的信息變成真正的圖，即打散成像素

?在《少年派的奇幻漂流》中的老虎栩栩如生，這是圖形學的貢獻，老虎身上有很多多邊形，經歷了變換操作后會形成在屏幕中的多邊形，要進一步把多邊形打碎成像素顯示在屏幕上，知曉每一個像素的值都是什么，這個過程叫做光柵化

圖像不止可以顯現到屏幕上，還有一些其他的繪畫工具

Drawing Machine

機器人的機械臂？：

激光切割：

Different Raster Displays

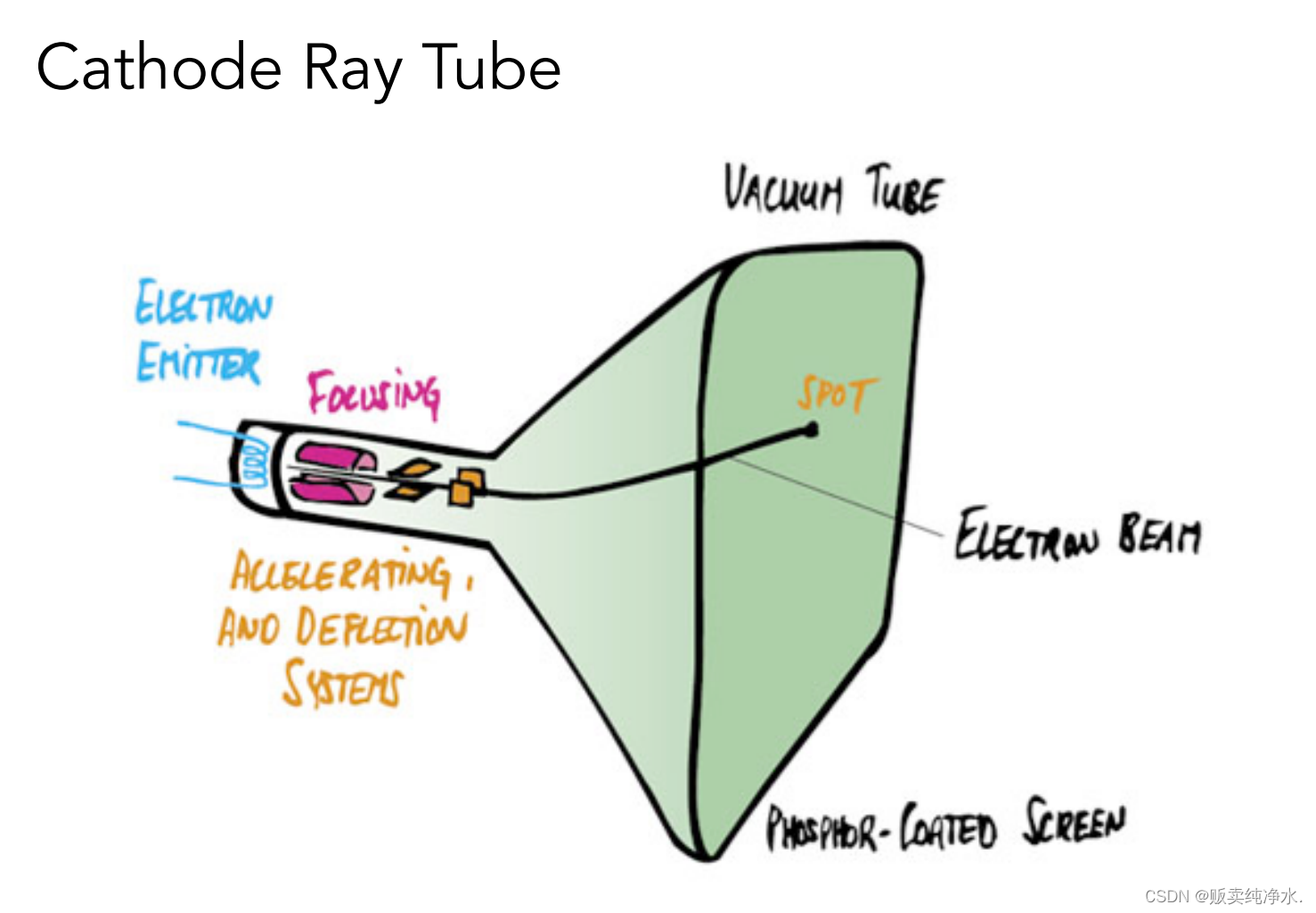
示波器：示波器本身也是成像的設備，它成像的原理和早期的顯示器基本相同，電子經過陰極射線管加速打到屏幕上（CRT屏幕）

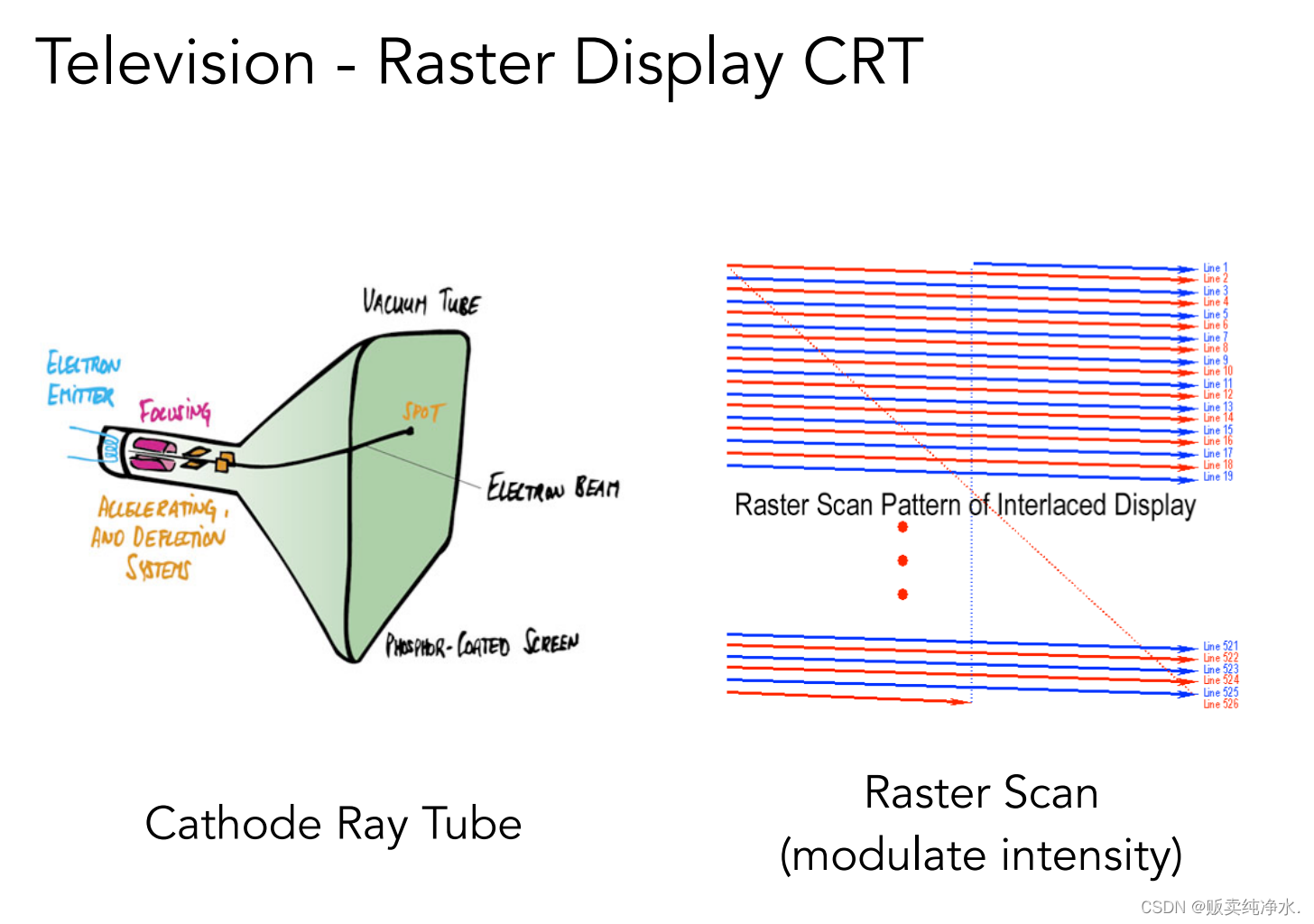
采用掃描的方式控制打印的位置，（隔行掃描，畫每張圖工作量減少一半，但對高速運動的畫面容易造成畫面撕裂）隔一行一條線，當足夠密集的時候就足以覆蓋整個屏幕：

?

顯示器🖥通過顯卡（內存中的一塊區域映射到屏幕上）：

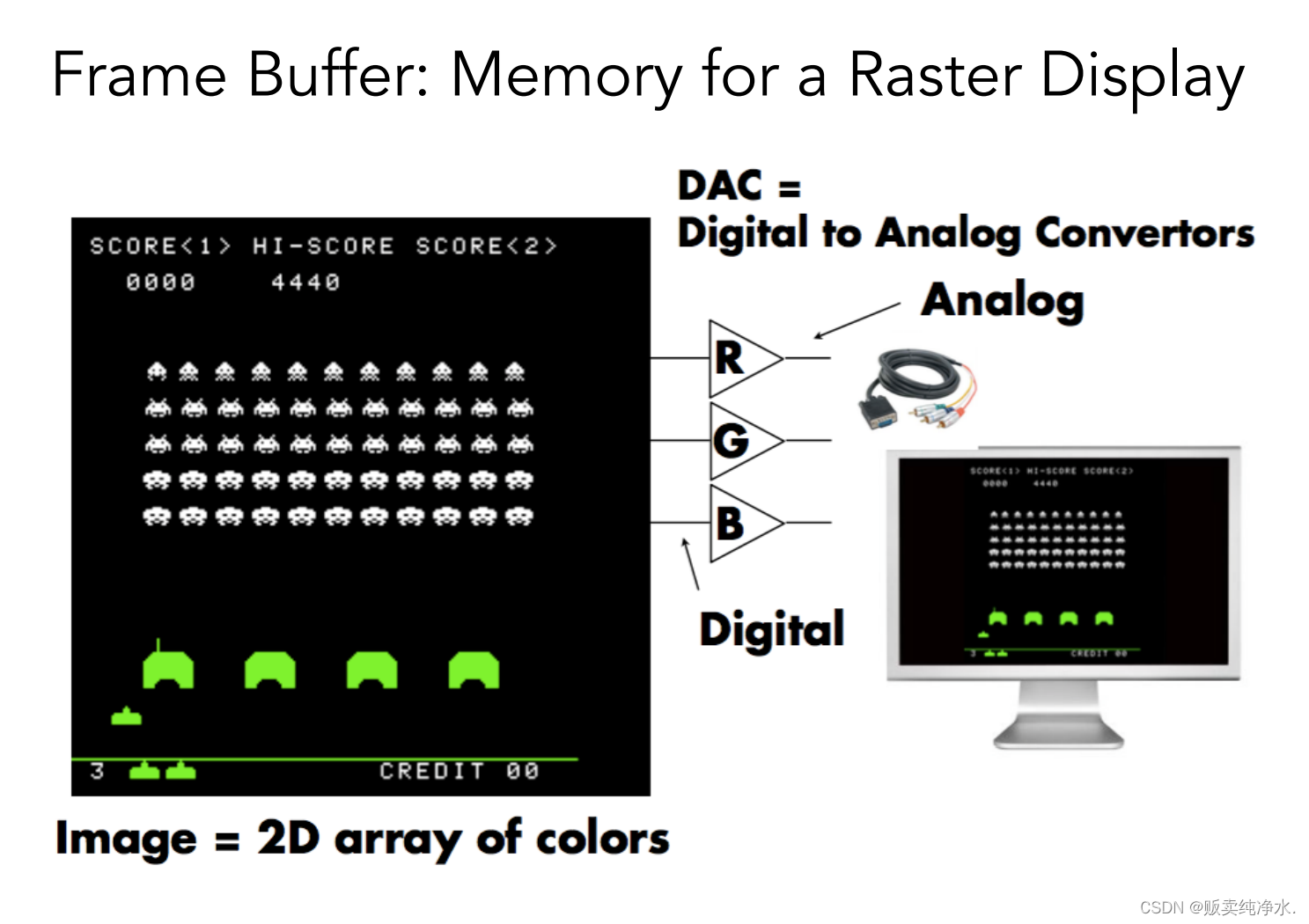
高分辨率顯示器，有些甚至分辨率超過了人的視網膜的分辨率（視網膜屏幕）：

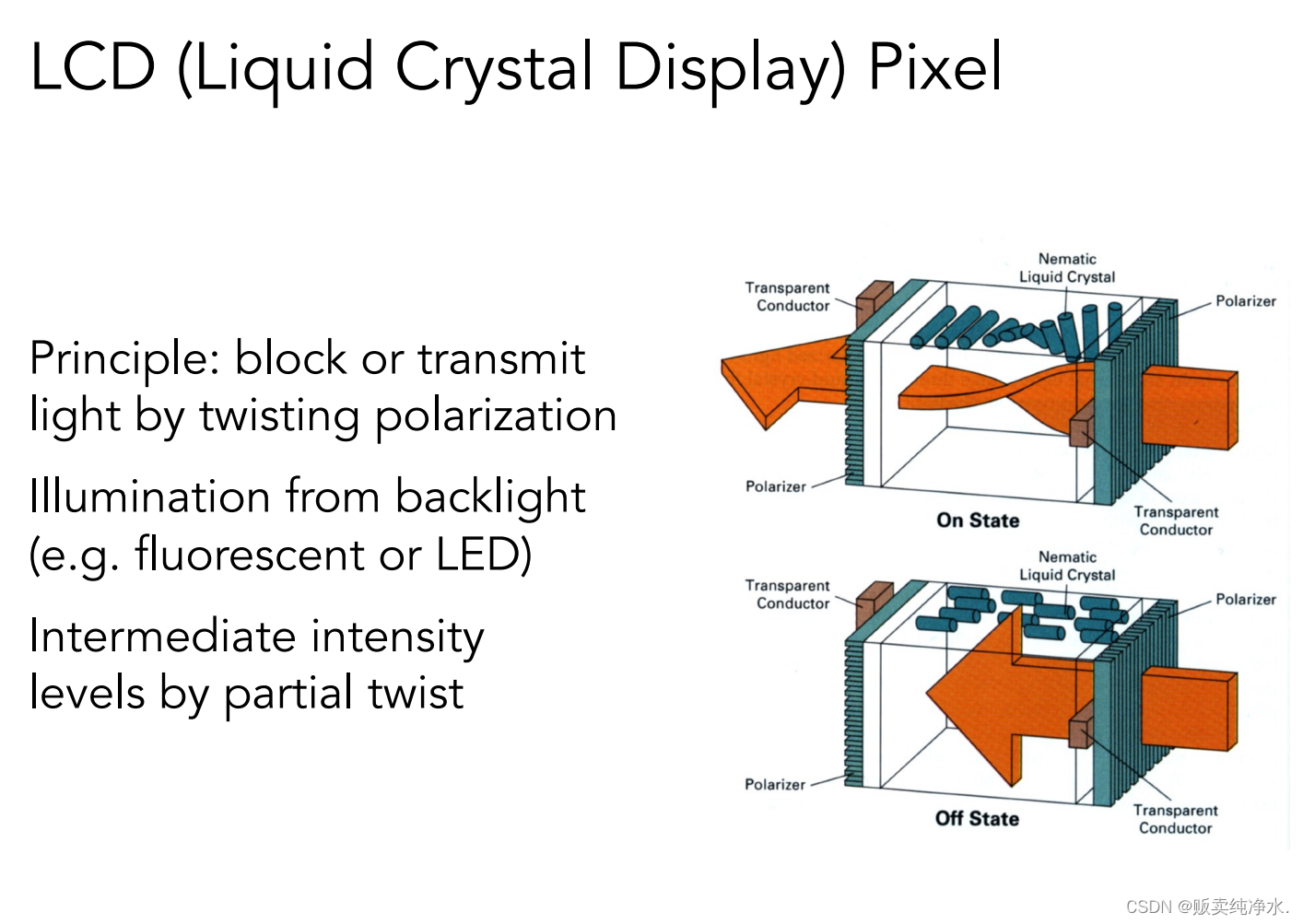
LCD（液晶顯示器）利用液晶的原理控制顯示

液晶通過自己的排布影響光的偏振方向（極化），兩個光柵不同方向排布

LED發光二極管：

墨水屏刷新有點慢，但是挺自然

三角形表示能力很強，可以表示很多二維三維中的圖形：

?

為什么三角形在圖形學中得到了如此廣泛的應用呢？?

?

首先三角形很簡單，任何東西多可以拆分成三角形，內部一定是平面的，內外很清晰，只要定義了三角形的三個頂點，可以明確的知道差值：

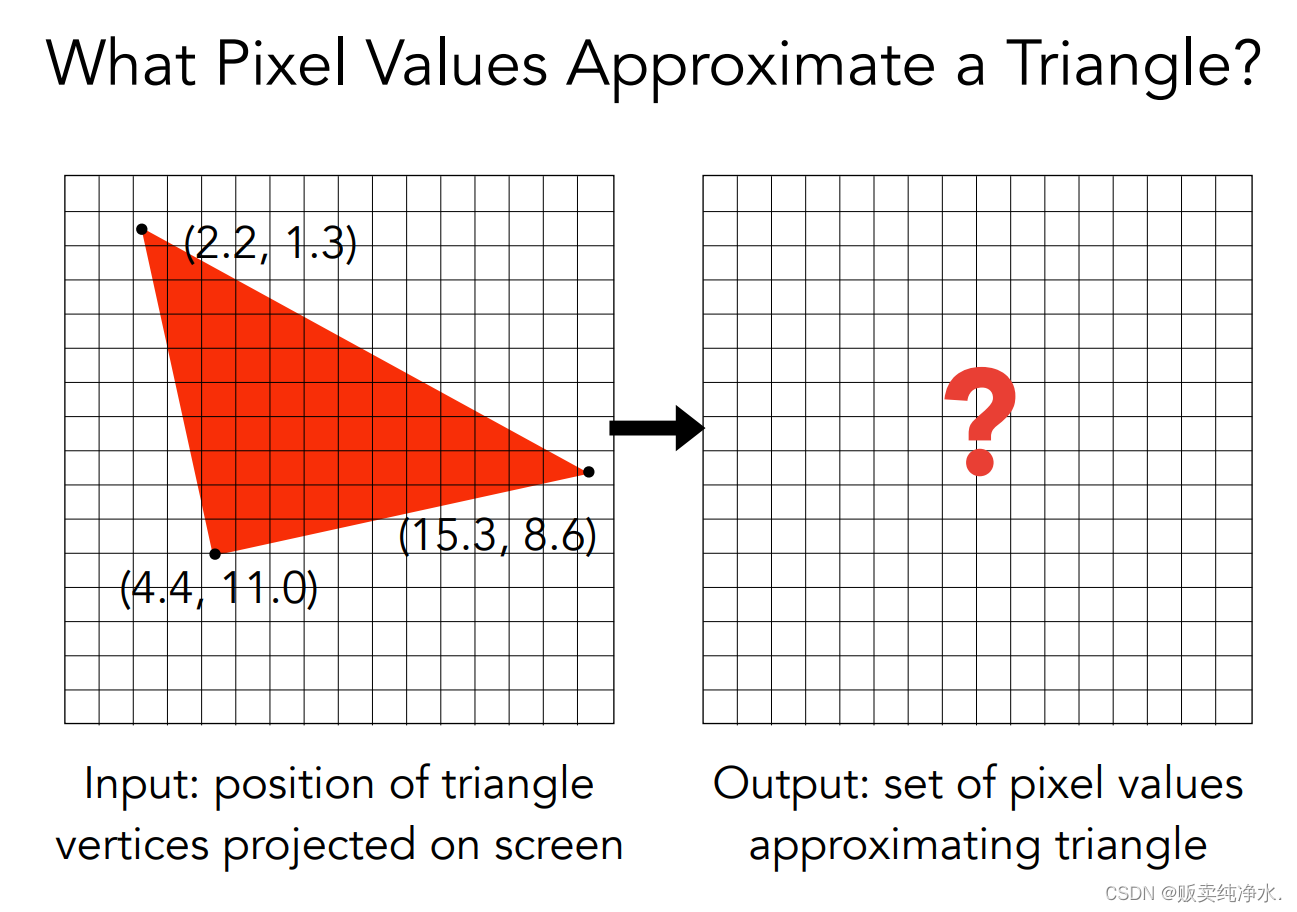
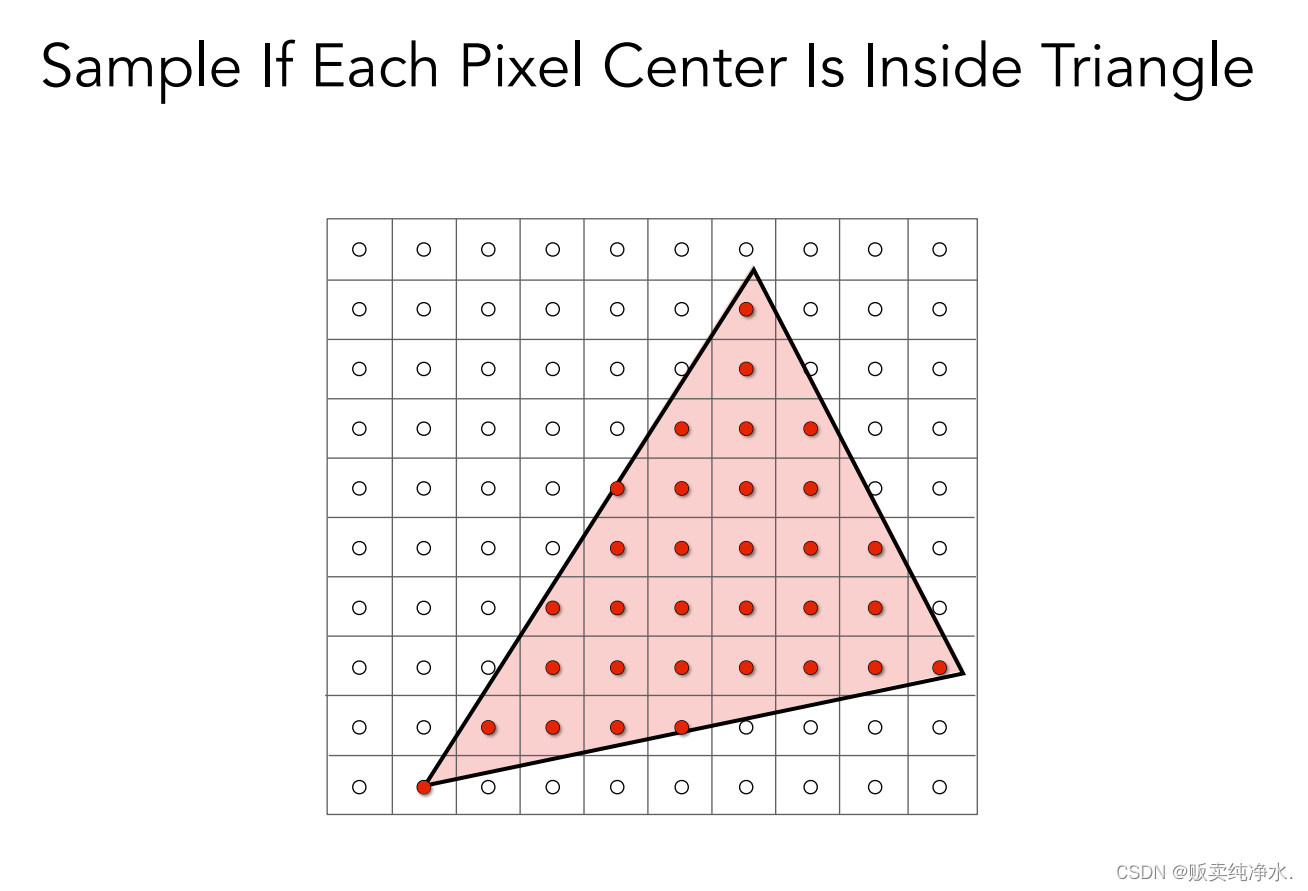
判斷像素和三角形的位置關系是光柵化中很重要的一環，像素內部是不能有顏色變化的，那蓋住一半的像素該怎么辦？

那就考慮像素中心點與三角形的位置關系唄：

?

?

?

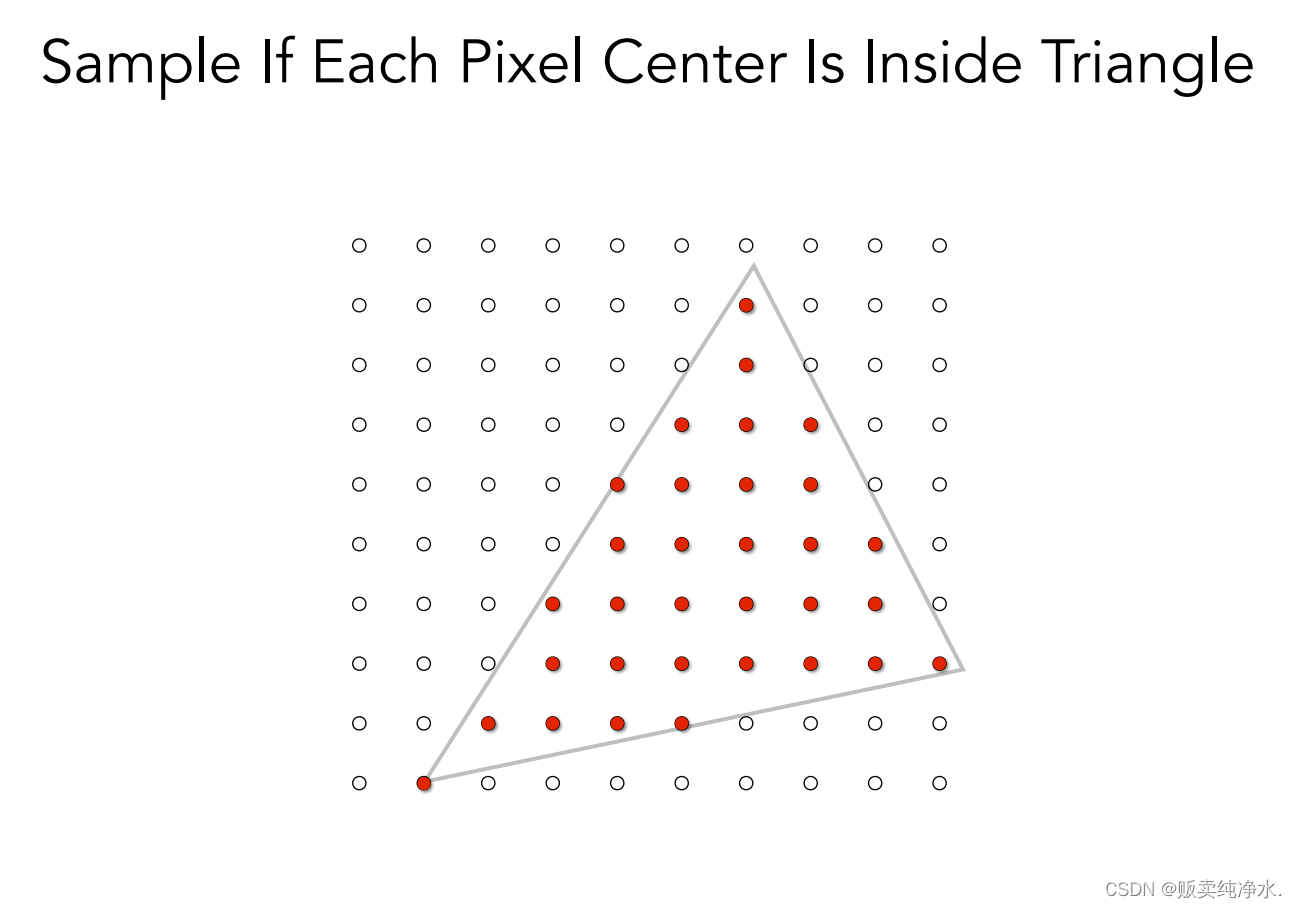
最簡單的光柵化方法：采樣，那么我們如何進行這樣的采樣呢？

可以這樣遍歷一個二維數組：

?inside是定義的一個函數，判斷點是否在三角形內（可以做叉積）：

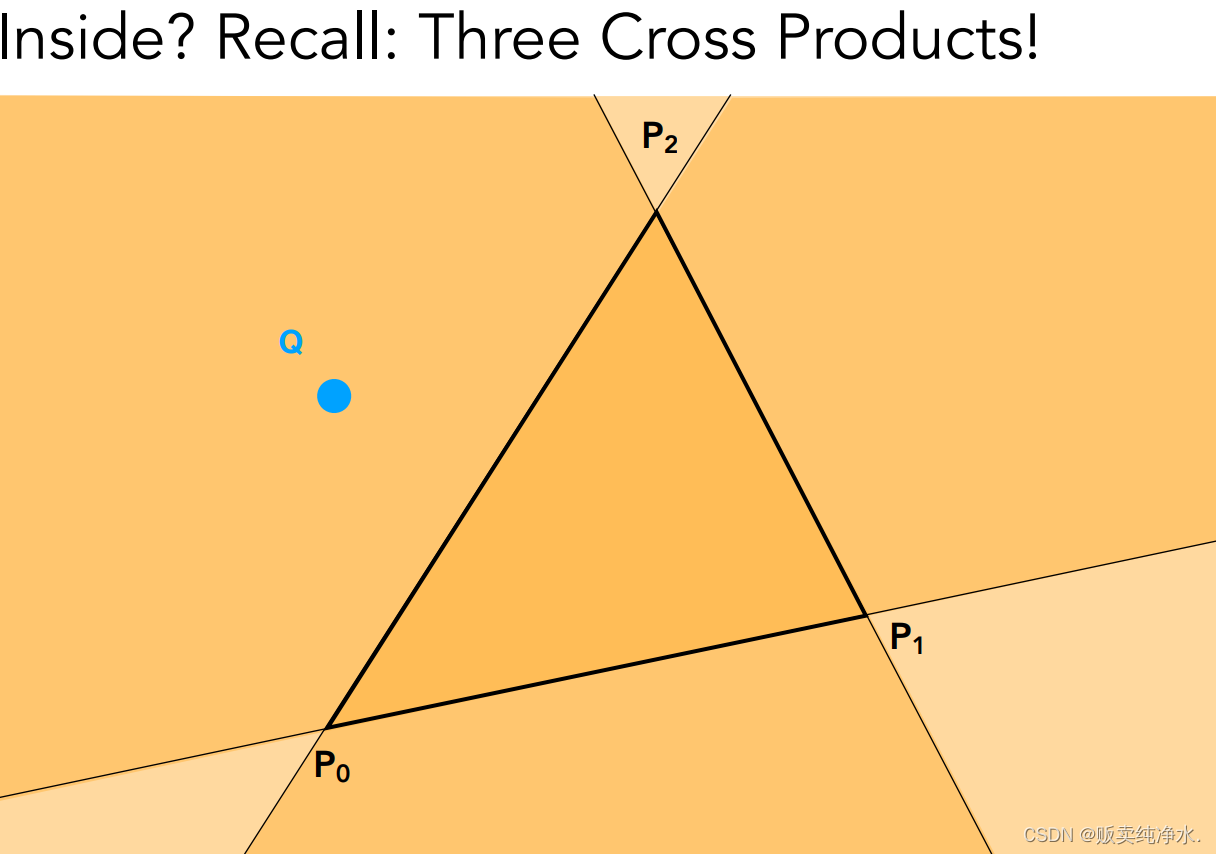
?那如果給定點恰好在三角形的邊界怎么辦？

那就要么不做處理，要么特殊處理（計上不計下，計左不計右）

通過采樣進行光柵化：

有的點不可能觸碰到三角形，三角形根本不可能填充到這些像素上，藍色區域：三角形的包圍盒

每一行都找最左和最右（包圍盒較大時比較適用）：

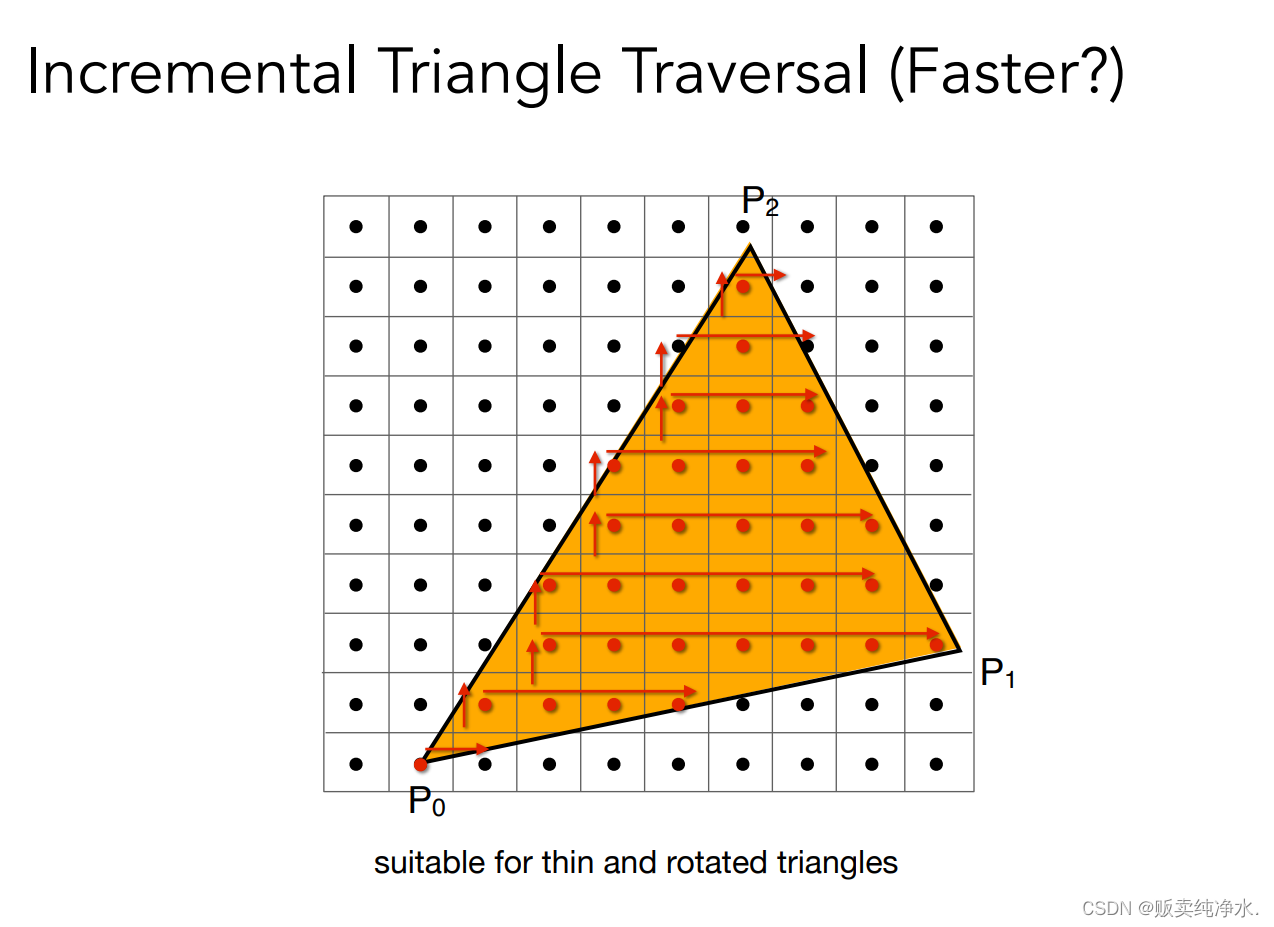
實際屏幕效果：

?

綠色像素多一點（人眼對綠色更為敏感，紅：藍：綠=1:1:2）?

我們仍然認為像素是一個內部顏色均勻的小方塊：

?

采樣后對應像素發現不太對：

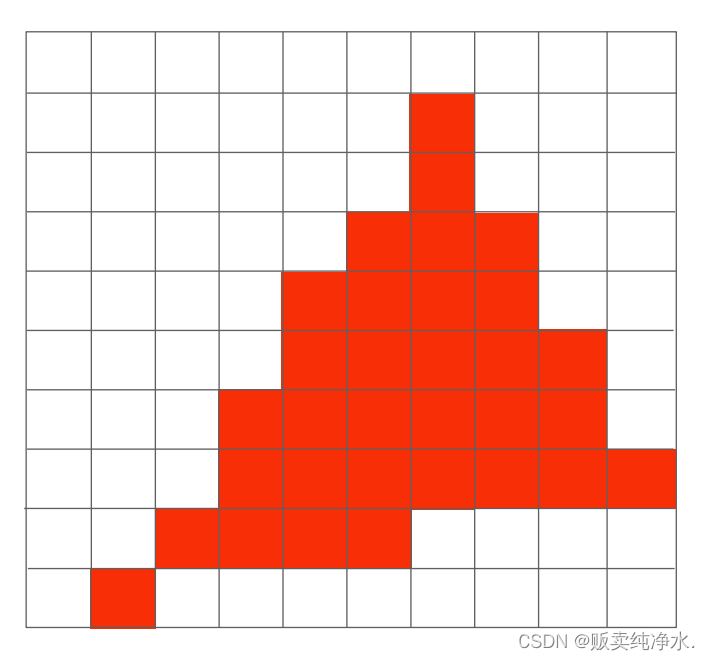
可是我們想要的不是這個嗎？

這鋸齒太明顯了吧？造成這個的結果呢就是因為鋸齒，鋸齒是圖形學中致力解決的一個問題，采樣率對于信號來說不夠高：走樣

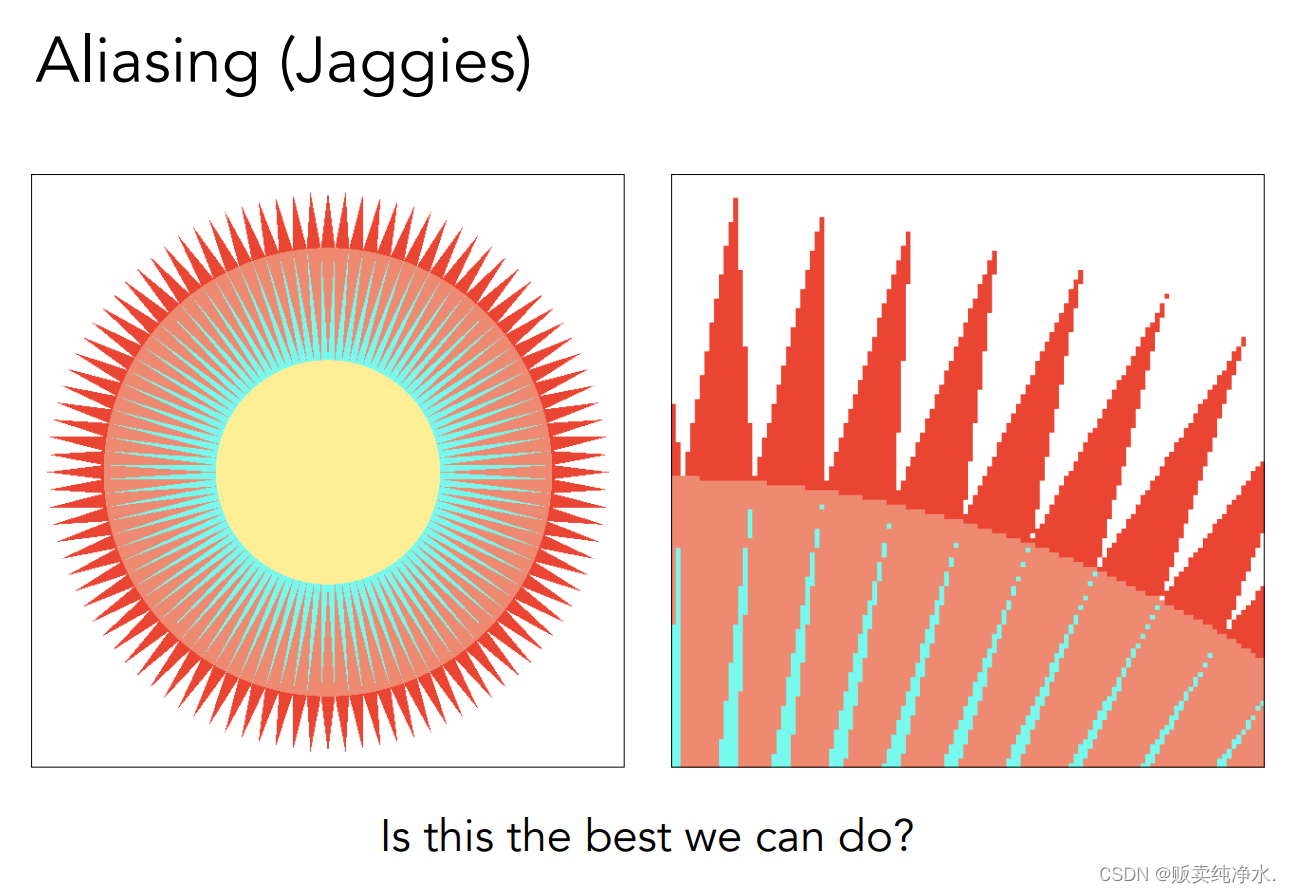
抗鋸齒、反走樣是圖形學中的一個重要技術