系列文章目錄
第一部分 KAN的理解——數學背景
第二部分 KAN的理解——網絡結構
第三部分 KAN的實踐——第一個例程
文章目錄
- 系列文章目錄
- 前言
- KAN 的第一個例程 get started
前言
這里記錄我對于KAN的探索過程,每次會嘗試理解解釋一部分問題。歡迎大家和我一起討論。
KAN tutorial
KAN 的第一個例程 get started
以下內容包含對于代碼的理解,對于KAN訓練過程的理解和代碼的解釋。并且包含代碼的結果。
- 對于KAN進行初始化。
from kan import *
# create a KAN: 2D inputs, 1D output, and 5 hidden neurons. cubic spline (k=3), 5 grid intervals (grid=5).
model = KAN(width=[2,5,1], grid=5, k=3, seed=0)
從上面的代碼可以看出,輸入兩維,說明要擬合的數據有兩個輸入變量,hidden neurons5個說明是全連接網絡,還沒有進行剪枝。
gird intervel表示用于擬合的樣條函數的一組離散點,這些點用于分段構造樣條函數。網格設定的約密集對于擬合的函數精度越高,想要提高網絡的擬合能力,一般會增加grid interval的數目,在論文中稱為grid extension。
這里的k是指一次樣條、二次樣條等這里的次數。表示在每個區間內擬合函數時,使用的是多少次數的多項式表示。
seed為隨機數種子,通過設置隨機數種子seed=0,模型的初始化(如權重初始化)和任何涉及隨機性的過程都會產生相同的結果。
- 創建數據集,用于作為訓練的輸入
# create dataset f(x,y) = exp(sin(pi*x)+y^2)
f = lambda x: torch.exp(torch.sin(torch.pi*x[:,[0]]) + x[:,[1]]**2)
dataset = create_dataset(f, n_var=2)
dataset['train_input'].shape, dataset['train_label'].shape
從輸出和函數定義來看,默認KAN的train number和test number都是1000
create_dataset函數的功能為生成一系列的數據字典,包括train_input,train_label,test_input,test_label
第一行lambda函數用于定義匿名函數,接收二維函數x為輸入,并返回一個新張量f,為其僅進行特定的數學運算并返回結果
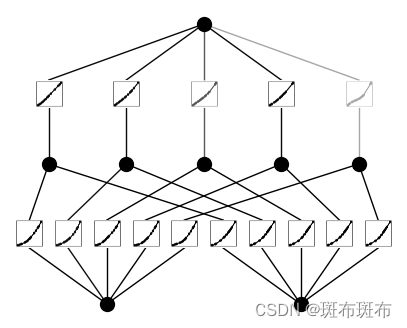
- 繪制初始化結果
# plot KAN at initialization
model(dataset['train_input'][:20]);
model.plot(beta=100,sample=True)
額外提一句,在做初始化的時候,這里的有一些默認參數沒給出來。
在初始化時,已經生成了每個節點的被學習的weight函數曲線的可視化,且被保存在./figures下,在初始化時添加了noise,所以每個節點的曲線形狀不同,且在定義模型時還有supervised mode和unsupervised mode可以選擇。
這部分代碼的功能主要是,在初始化網絡時給出了初始化時的可視化。結果如下:
- 模型訓練并設置對應的參數
# train the model
model.train(dataset, opt="LBFGS", steps=20, lamb=0.01, lamb_entropy=10.);
一些參數:
dataset:輸入的訓練數據
opt:優化算法選擇,有LBFGS和Adam算法可供選擇,分別問基于二階導數的算法和基于一階導數的優化算法
step:訓練步數
lamb:控制整體正則化項的強度,能夠增強訓練的稀疏性,保留有效項
lamb_entropy:控制熵正則化項的強度,能有效減少激活函數的數量,避免出現相同或非常相似的函數
從代碼的內容上看,在訓練中,已經在進行有效項的保留,重復項的去除。
1000的數據量大概要處理11s
畫出此時的第一次訓練后的圖,發現被判定為不重要的項的透明度增強了許多,在圖上顯示表示為不重要的部分。
結果如下:
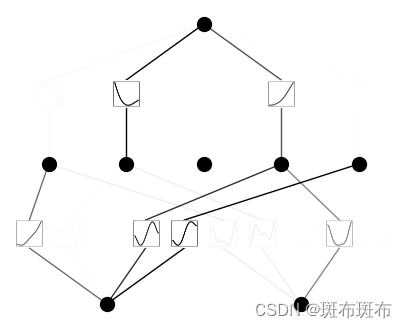
- 剪枝
# model.prune(mode='manual',active_neurons_id=[[3],[2]] )
model.prune()
model.plot(mask=False)
做一些剪枝,直接減掉一些不重要的node。prune的原則是查看每個node的入邊和出邊,
如果某個節點所連接的入邊和出邊的屬于不重要的邊,那么這些邊可以被剪枝。
這里的默認參數是自動剪枝,但是實際上也可以選擇手動剪枝,確要保留的節點。
- 再剪枝
model = model.prune()
model(dataset['train_input'][:20])
model.plot(sample=True)
再剪枝,得到更小的模型。這里的dataset[‘train_input’]應該是用來測試目前的訓練結果的。結果如下:
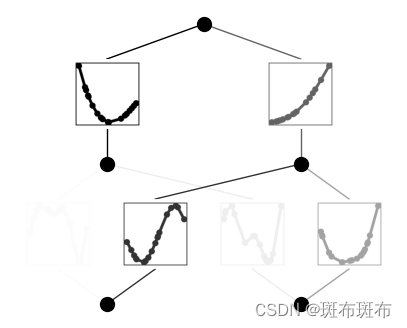
- 再訓練
model.train(dataset, opt="LBFGS", steps=50);
現在得到的結果是去掉了一些node的結果,在更少的nodes被保留的情況下,繼續進行訓練
從訓練的結果可以結案到現在的精確度變高了,可能是因為減少了node,保留了可信度更強的node
- 再看一遍訓練結果。
model.plot()
結果如下:

- 確定要fix的項
mode = "auto" # "manual"
# 設置mannual會報錯if mode == "manual":# manual mode# fix_symbolic()方程下的參數,(layer index,layer index,output neuron index)model.fix_symbolic(0,0,0,'sin');model.fix_symbolic(0,1,0,'x^2');model.fix_symbolic(1,0,0,'exp');
elif mode == "auto":# automatic modelib = ['x','x^2','x^3','x^4','exp','log','sqrt','tanh','sin','abs']model.auto_symbolic(lib=lib)
結果如下:

- 最后輸出數學表達式
model.train(dataset, opt="LBFGS", steps=50);
model.symbolic_formula()[0][0]
這里可能出現的問題是,會多余出一些小項,比如預測了正確的公式但是結尾部分會加上一個很小的數值,或者加上一個值很小的表達式。
結果如下:
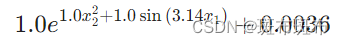







)











