一、歸并排序思想
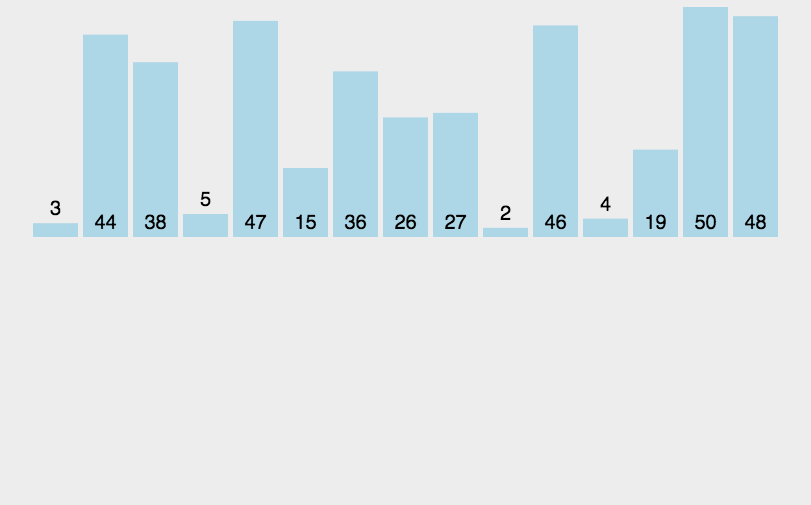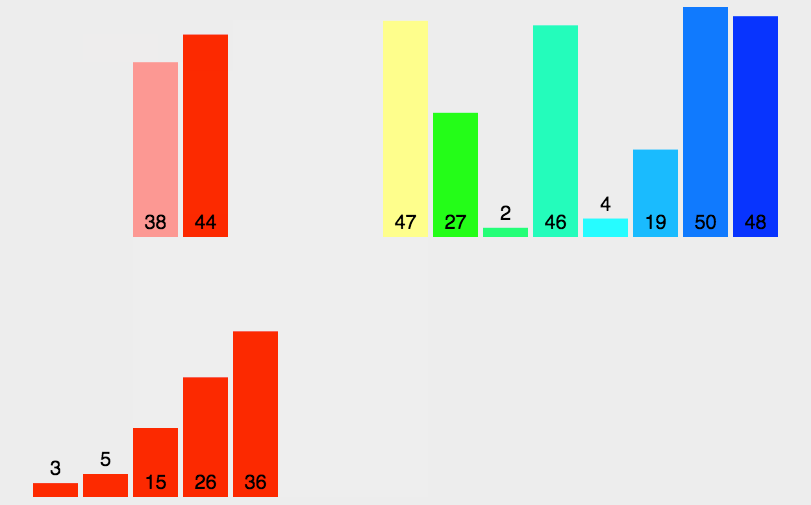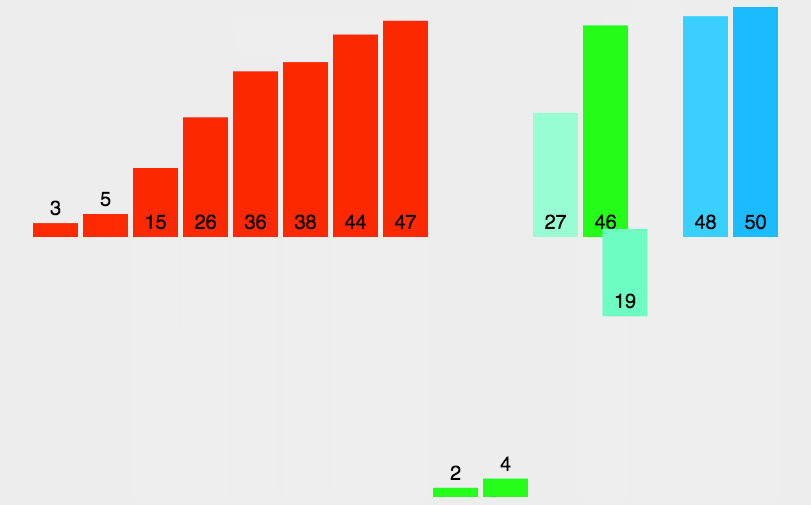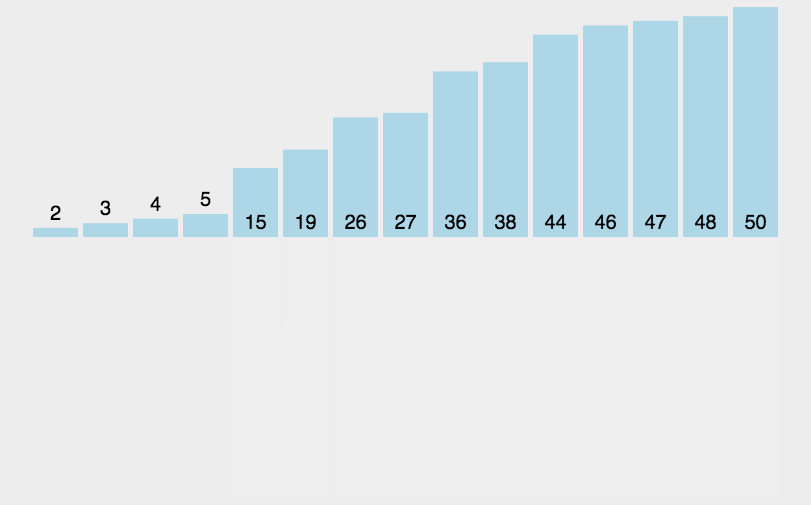
歸并排序(MERGE-SORT)是建立在歸并操作上的一種有效的排序算法,該算法是采用分治法(Divide andConquer)的一個非常典型的應用。將已有序的子序列合并,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合并成一個有序表,稱為二路歸并。 歸并排序核心步驟?:
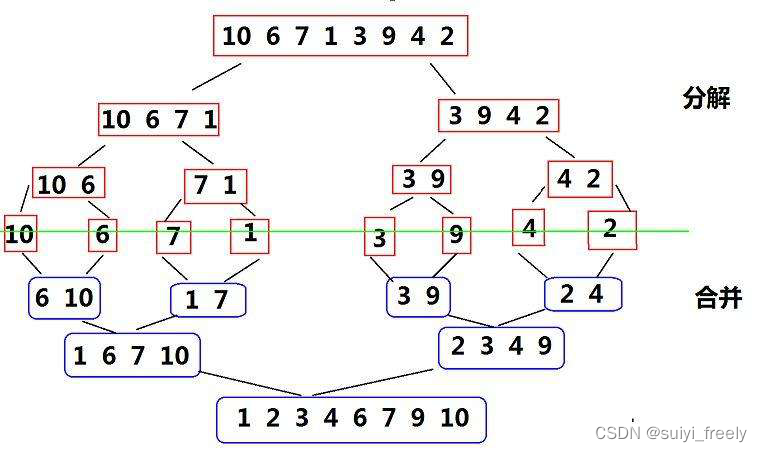
我們現在要樹立這么一個思路,分解數組并不是真的分解數組,而是可以通過下標的形式來區分數組。歸并排序實際上就是將一個數組分解到不能子啊分解的部分,兩兩經行比較排序,再將數據更新到新的數組中去。這非常類似于我們學的數的后序遍歷。
二、代碼實現
1、單趟:
我們先寫單趟,因為歸并排序是對半分組,所以最后為兩個區間經行比較,思路轉化為之前我們學過的兩個數組的合并
int mid = (rigt + left) / 2;
int begin1 = left;
int end1 = mid-1;
int begin2 = mid;
int end2 = rigt;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{if (a[begin1] > a[begin2]){tmp[i++] = a[begin2++];}else{tmp[i++] = a[begin1++];}
}
while (begin1<=end1)
{tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{tmp[i++] = a[begin2++];
}
memcpy(a+left, tmp+left, sizeof(int) * (rigt - left + 1));這里要注意兩個問題:1、區間怎么劃分合適,2、為什么每排序一次就得將數組拷貝回去
?2、單趟問題解釋
首先我們先解決第一個問題:區間怎么劃分合適?
我們這里以下面圖為例:
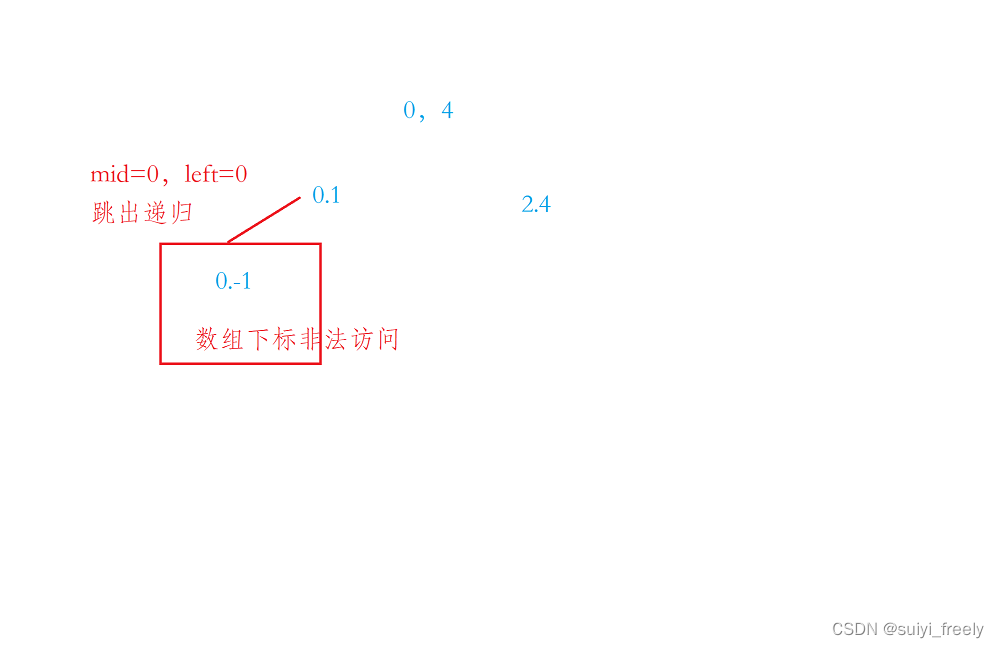
因為有-1的存在很容易導致下標為負數,最后導致數組的違法訪問。同時可能還會有死循環的問題:
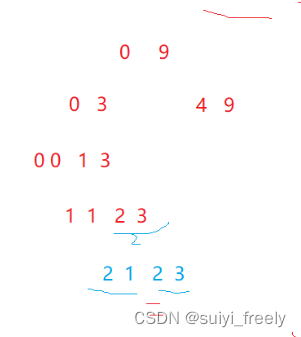
具體原因如下:

但是如果改為區間為?
int begin1 = left;
int end1 = mid;
int begin2 = mid+1;
int end2 = rigt;就不會出現這個問題:

所以正確代碼如下:
int mid = (rigt + left) / 2;
int begin1 = left;
int end1 = mid;
int begin2 = mid+1;
int end2 = rigt;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{if (a[begin1] > a[begin2]){tmp[i++] = a[begin2++];}else{tmp[i++] = a[begin1++];}
}
while (begin1<=end1)
{tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{tmp[i++] = a[begin2++];
}
memcpy(a+left, tmp+left, sizeof(int) * (rigt - left + 1));第二個問題:因為比較的時候是在原數組經行比較如果不及時將數組內容更新,可能會導致再排序時經行錯誤的大小比較,最后導致結果錯誤?
3、總體代碼實現
結束條件當分割區間等于1或者小于1的時候。
void _MergeSort(int* a, int* tmp, int left, int rigt)
{if (left >= rigt){return;}int mid = (rigt + left) / 2;_MergeSort(a, tmp, left, mid);_MergeSort(a, tmp, mid + 1, rigt);int begin1 = left;int end1 = mid;int begin2 = mid+1;int end2 = rigt;int i = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] > a[begin2]){tmp[i++] = a[begin2++];}else{tmp[i++] = a[begin1++];}}while (begin1<=end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a+left, tmp+left, sizeof(int) * (rigt - left + 1));
}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){return;}else{_MergeSort(a, tmp, 0, n - 1);free(tmp);tmp = NULL;}
}
三、非遞歸
對于歸并排序我們實現非遞歸用循環更好一點,非遞歸我們可以直接從遞歸回去那出發,定義一個組個數,通過控制組的個數實現“并”這個過程:
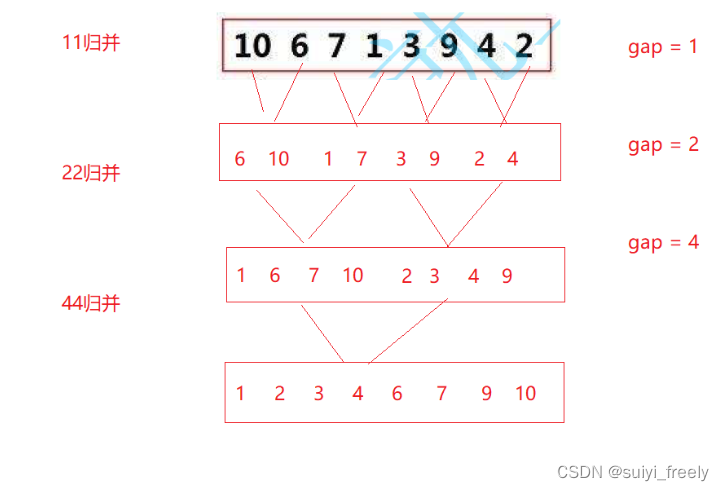
還是我們先寫一個數組只有一個數的情況:

for (int i = 0; i < end - begin + 1; i += 2 * gap)//每次比較兩組,所以加2gap
{int begin1 = i;int end1 = begin1 + gap - 1;int begin2 = begin1 + 2 * gap - 1;//第二組的開頭與第一組的開頭差2倍int end2 = begin2 + gap - 1;int k = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] > a[begin2]){tmp[k++] = a[begin2++];}else{tmp[k++] = a[begin1++];}}while (begin1 <= end1){tmp[k++] = a[begin1++];}while (begin2 <= end2){tmp[k++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (2 * gap));//同理這里也得排序一次就拷貝回去}那么后面就是gap*2控制即可:
void _MergeSortNonR(int* a, int* tmp,int begin, int end)
{int gap = 1;for (int j = gap; j < end-begin+1; j *= 2){for (int i = 0; i < end - begin + 1; i += 2 * gap)//每次比較兩組,所以加2gap{int begin1 = i;int end1 = begin1 + gap - 1;int begin2 = begin1 + 2 * gap - 1;//第二組的開頭與第一組的開頭差2倍int end2 = begin2 + gap - 1;int k = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] > a[begin2]){tmp[k++] = a[begin2++];}else{tmp[k++] = a[begin1++];}}while (begin1 <= end1){tmp[k++] = a[begin1++];}while (begin2 <= end2){tmp[k++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (2 * gap));}}
}但是上面的代碼仍然存在問題,和快排類似這里會存在數組越界問題:這里我們打印數組下標區間來觀察一下:、
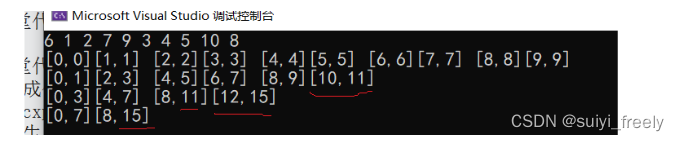
大致我們可以分為這兩種情況:

?如果end1越界,那么說明分為了只有這一組數據,不用排了直接跳出循環,如果end2越界我們就需要給end2修改值。
所以改進代碼如下:
void _MergeSortNonR(int* a, int* tmp,int begin, int end)
{int gap = 1;for (int j = gap; j < end-begin+1; j *= 2){for (int i = 0; i < end - begin + 1; i += 2 * gap)//每次比較兩組,所以加2gap{int begin1 = i;int end1 = begin1 + gap - 1;int begin2 = begin1 + 2 * gap - 1;//第二組的開頭與第一組的開頭差2倍int end2 = begin2 + gap - 1;int k = i;// 第二組都越界不存在,這一組就不需要歸并if (begin2 >= end - begin + 1)break;// 第二的組begin2沒越界,end2越界了,需要修正一下,繼續歸并if (end2 >= end - begin + 1)end2 = end - begin + 1 - 1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] > a[begin2]){tmp[k++] = a[begin2++];}else{tmp[k++] = a[begin1++];}}while (begin1 <= end1){tmp[k++] = a[begin1++];}while (begin2 <= end2){tmp[k++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (2 * gap));}}
}
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){return;}else{_MergeSortNonR(a, tmp, 0, n - 1);free(tmp);tmp = NULL;}
}
可能有人會想如果只剩一組數據了,我直接return行不行?實際上是可以的,因為break跳出循環后在gap*2還是只有一組數據,所以直接return即可。






)












)