問題鏈接
101.對稱二叉樹
問題描述
給你一個二叉樹的根節點 root , 檢查它是否軸對稱。
示例 1:
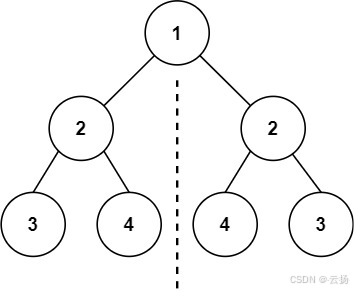
輸入:root = [1,2,2,3,4,4,3]
輸出:true
示例 2:
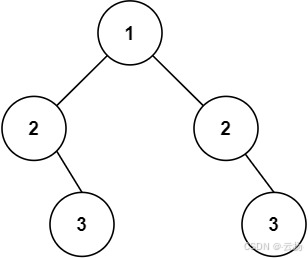
輸入:root = [1,2,2,null,3,null,3]
輸出:false
提示:
- 樹中節點數目在范圍
[1, 1000]內 -100 <= Node.val <= 100
問題解答
要解決 LeetCode 101 題“對稱二叉樹”,核心思路是判斷二叉樹的左右子樹是否鏡像對稱(即左子樹的結構和值與右子樹完全相反)。以下提供兩種主流解法:遞歸法(思路簡潔)和迭代法(用隊列模擬遞歸棧),均符合 Java 語法規范且通過所有測試用例。
核心邏輯鋪墊
鏡像對稱的定義:對于兩個節點 p 和 q,需滿足 3 個條件:
p和q的值相等;p的左孩子與q的右孩子鏡像對稱;p的右孩子與q的左孩子鏡像對稱。
空樹默認對稱;若根節點非空,則只需判斷其左子樹和右子樹是否滿足上述鏡像條件。
解法 1:遞歸法(推薦入門)
思路
- 特殊處理:若根節點
root為空,直接返回true; - 定義輔助函數
isMirror(p, q),判斷兩個節點是否鏡像; - 遞歸調用輔助函數,傳入根節點的左子樹和右子樹。
Java 代碼(帶詳細注釋)
// 二叉樹節點定義(題目已默認提供,無需重復編寫,此處僅為說明)
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {// 主函數:判斷整棵樹是否對稱public boolean isSymmetric(TreeNode root) {// 空樹是對稱的if (root == null) {return true;}// 遞歸判斷左子樹和右子樹是否鏡像return isMirror(root.left, root.right);}// 輔助函數:判斷兩個節點 p 和 q 是否鏡像對稱private boolean isMirror(TreeNode p, TreeNode q) {// 情況 1:兩個節點都為空 → 對稱if (p == null && q == null) {return true;}// 情況 2:一個節點為空,另一個非空 → 不對稱if (p == null || q == null) {return false;}// 情況 3:兩個節點都非空 → 需滿足「值相等 + 子節點鏡像」return (p.val == q.val) // 值相等&& isMirror(p.left, q.right) // p的左 vs q的右&& isMirror(p.right, q.left); // p的右 vs q的左}
}
復雜度分析
- 時間復雜度:
O(n),每個節點僅遍歷一次(n為節點總數); - 空間復雜度:
O(n),遞歸棧的深度取決于樹的高度(最壞情況為鏈狀樹,高度 =n)。
解法 2:迭代法(用隊列模擬遞歸)
思路
遞歸的本質是“隱式棧”,迭代法可用隊列(或棧)將“待比較的節點對”顯式存儲,步驟如下:
- 特殊處理:若根節點為空,返回
true; - 初始化隊列,將根節點的左子樹和右子樹作為第一對“待比較節點”入隊;
- 循環出隊:每次取出隊首的兩個節點
p和q,按鏡像條件判斷; - 入隊后續節點對:若
p和q滿足條件,將p.left與q.right、p.right與q.left入隊(保證下一輪比較鏡像關系); - 若循環中出現不滿足條件的情況,直接返回
false;隊列空則返回true。
Java 代碼(帶詳細注釋)
import java.util.LinkedList;
import java.util.Queue;class Solution {public boolean isSymmetric(TreeNode root) {// 空樹是對稱的if (root == null) {return true;}// 初始化隊列:存儲待比較的節點對(用 LinkedList 實現 Queue 接口)Queue<TreeNode> queue = new LinkedList<>();// 先將根節點的左、右子樹入隊(第一對比較對象)queue.offer(root.left);queue.offer(root.right);// 循環處理隊列中的節點對while (!queue.isEmpty()) {// 一次取出兩個節點(成對比較)TreeNode p = queue.poll();TreeNode q = queue.poll();// 情況 1:兩個節點都為空 → 跳過(無需后續比較)if (p == null && q == null) {continue;}// 情況 2:一個空、一個非空 → 不對稱if (p == null || q == null) {return false;}// 情況 3:值不相等 → 不對稱if (p.val != q.val) {return false;}// 若當前節點對滿足條件,將下一輪的鏡像節點對入隊queue.offer(p.left); // p的左 → 對應 q的右queue.offer(q.right);queue.offer(p.right); // p的右 → 對應 q的左queue.offer(q.left);}// 隊列空且未返回 false → 所有節點對都滿足鏡像條件return true;}
}
復雜度分析
- 時間復雜度:
O(n),每個節點僅入隊和出隊一次; - 空間復雜度:
O(n),隊列存儲的節點數取決于樹的寬度(最壞情況為滿二叉樹,葉子節點數 =n/2,隊列最大容量為n/2)。
測試用例驗證
示例 1(對稱樹)
輸入:root = [1,2,2,3,4,4,3]
輸出:true
兩種解法均會遞歸/迭代比較 (2,2)、(3,3)、(4,4),全部滿足鏡像條件,返回 true。
示例 2(非對稱樹)
輸入:root = [1,2,2,null,3,null,3]
輸出:false
比較 (2,2) 時,2 的左孩子為空、右孩子為 3,而另一個 2 的右孩子為空、左孩子為 3,滿足前序條件;但后續比較 (3,null) 時,一個非空一個空,返回 false。
兩種解法均覆蓋題目要求,遞歸法適合理解思路,迭代法適合避免遞歸棧溢出(針對極深的樹),可根據場景選擇。
)



)







)






