【本節目標】

1. 掌握樹的基本概念
2. 掌握二叉樹概念及特性
3. 掌握二叉樹的基本操作
4. 完成二叉樹相關的面試題練習

1. 樹型結構（了解）

1.1 概念

樹是一種非線性的數據結構，它是由n（n>=0）個有限結點組成一個具有層次關系的集合。把它叫做樹是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。它具有以下的特點：

• 有一個特殊的結點，稱為根結點，根結點沒有前驅結點
• 除根結點外，其余結點被分成M(M > 0)個互不相交的集合T1、T2、…、Tm，其中每一個集合Ti (1 <= i <=m) 又是一棵與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，可以有0個或多個
• 后繼樹是遞歸定義的。

注意：樹形結構中，子樹之間不能有交集，否則就不是樹形結構

1.2 概念（重要）

結點的度：一個結點含有子樹的個數稱為該結點的度； 如上圖：A的度為6
樹的度：一棵樹中，所有結點度的最大值稱為樹的度； 如上圖：樹的度為6
葉子結點或終端結點：度為0的結點稱為葉結點； 如上圖：B、C、H、I…等節點為葉結點
雙親結點或父結點：若一個結點含有子結點，則這個結點稱為其子結點的父結點； 如上圖：A是B的父結點
孩子結點或子結點：一個結點含有的子樹的根結點稱為該結點的子結點； 如上圖：B是A的孩子結點
根結點：一棵樹中，沒有雙親結點的結點；如上圖：A
結點的層次：從根開始定義起，根為第1層，根的子結點為第2層，以此類推
樹的高度或深度：樹中結點的最大層次； 如上圖：樹的高度為4

樹的以下概念只需了解，在看書時只要知道是什么意思即可：
非終端結點或分支結點：度不為0的結點； 如上圖：D、E、F、G…等節點為分支結點
兄弟結點：具有相同父結點的結點互稱為兄弟結點； 如上圖：B、C是兄弟結點
堂兄弟結點：雙親在同一層的結點互為堂兄弟；如上圖：H、I互為兄弟結點
結點的祖先：從根到該結點所經分支上的所有結點；如上圖：A是所有結點的祖先
子孫：以某結點為根的子樹中任一結點都稱為該結點的子孫。如上圖：所有結點都是A的子孫
森林：由m（m>=0）棵互不相交的樹組成的集合稱為森林

1.3 樹的表示形式（了解）

樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，實際中樹有很多種表示方式，如：雙親表示法，孩子表示法、孩子雙親表示法、孩子兄弟表示法等等。我們這里就簡單的了解其中最常用的孩子兄弟表示法。

class Node {int value; // 樹中存儲的數據Node firstChild; // 第一個孩子引用Node nextBrother; // 下一個兄弟引用
}

1.4 樹的應用

文件系統管理（目錄和文件）

2. 二叉樹（重點）

2.1 概念

一棵二叉樹是結點的一個有限集合，該集合：

1. 或者為空
2. 或者是由一個根節點加上兩棵別稱為左子樹和右子樹的二叉樹組成
   
   從上圖可以看出：
3. 二叉樹不存在度大于2的結點
4. 二叉樹的子樹有左右之分，次序不能顛倒，因此二叉樹是有序樹
   注意：對于任意的二叉樹都是由以下幾種情況復合而成的：
   

2.2 兩種特殊的二叉樹

1. 滿二叉樹: 一棵二叉樹，如果每層的結點數都達到最大值，則這棵二叉樹就是滿二叉樹。也就是說，如果一棵二叉樹的層數為k，且結點總數是2^K-1，則它就是滿二叉樹。
2. 完全二叉樹: 完全二叉樹是效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。對于深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從0至n-1的結點一一對應時稱之為完全二叉樹。 要注意的是滿二叉樹是一種特殊的完全二叉樹。
   

2.3 二叉樹的性質

1. 若規定根結點的層數為1，則一棵非空二叉樹的第i層上最多有2^i-1 (i>0)個結點
2. 若規定只有根結點的二叉樹的深度為1，則深度為K的二叉樹的最大結點數是 (k>=0)
3. 對任何一棵二叉樹, 如果其葉結點個數為 n0, 度為2的非葉結點個數為 n2,則有n0＝n2＋1
   
4. 具有n個結點的完全二叉樹的深度k為log₂(n+1) 上取整
5. 對于具有n個結點的完全二叉樹，如果按照從上至下從左至右的順序對所有節點從0開始編號，則對于序號為 i 的結點有：

• 若i>0，雙親序號：(i-1)/2；i=0，i為根結點編號，無雙親結點
• 若2i+1<n，左孩子序號：2i+1，否則無左孩子
• 若2i+2<n，右孩子序號：2i+2，否則無右孩子

1. 某二叉樹共有 399 個結點，其中有 199 個度為 2 的結點，則該二叉樹中的葉子結點數為（ ）
   A 不存在這樣的二叉樹
   B 200
   C 198
   D 199
2. 在具有 2n 個結點的完全二叉樹中，葉子結點個數為（ ）
   A n
   B n+1
   C n-1
   D n/2
3. 一個具有767個節點的完全二叉樹，其葉子節點個數為（）
   A 383
   B 384
   C 385
   D 386
4. 一棵完全二叉樹的節點數為531個，那么這棵樹的高度為（ ）
   A 11
   B 10
   C 8
   D 12

答案：

1. B
   n0 = n2+1
2. A
   2n= n0 +1+ n2
   n0 = n2+1
   假設度為0的節點個數為x
   n2 =n0-1 =x-1
   2n =x+1+x-1
   2n = 2x
   n=x
3. B
4. B

2.4 二叉樹的存儲

二叉樹的存儲結構分為：順序存儲和類似于鏈表的鏈式存儲。
順序存儲在下節介紹。
二叉樹的鏈式存儲是通過一個一個的節點引用起來的，常見的表示方式有二叉和三叉表示方式，具體如下

// 孩子表示法
class Node {int val; // 數據域Node left; // 左孩子的引用，常常代表左孩子為根的整棵左子樹Node right; // 右孩子的引用，常常代表右孩子為根的整棵右子樹
}
// 孩子雙親表示法
class Node {int val; // 數據域Node left; // 左孩子的引用，常常代表左孩子為根的整棵左子樹Node right; // 右孩子的引用，常常代表右孩子為根的整棵右子樹Node parent; // 當前節點的根節點
}

孩子雙親表示法后序在平衡樹位置介紹，本文采用孩子表示法來構建二叉樹。

2.5 二叉樹的基本操作

2.5.1 前置說明

在學習二叉樹的基本操作前，需先要創建一棵二叉樹，然后才能學習其相關的基本操作。由于現在大家對二叉樹結構掌握還不夠深入，為了降低大家學習成本，此處手動快速創建一棵簡單的二叉樹，快速進入二叉樹操作學習，等二叉樹結構了解的差不多時，反過頭再來研究二叉樹真正的創建方式。

public class BinaryTree{public static class BTNode{BTNode left;BTNode right;int value;BTNode(int value){this.value = value;}}private BTNode root;public void createBinaryTree(){BTNode node1 = new BTNode(1);BTNode node1 = new BTNode(2);BTNode node1 = new BTNode(3);BTNode node1 = new BTNode(4);BTNode node1 = new BTNode(5);BTNode node1 = new BTNode(6);root = node1;node1.left = node2;node2.left = node3;node1.right = node4;node4.left = node5;node5.right = node6;}
}

注意：上述代碼并不是創建二叉樹的方式，真正創建二叉樹方式后序詳解重點講解。
再看二叉樹基本操作前，再回顧下二叉樹的概念，二叉樹是：

1. 空樹
2. 非空：根節點，根節點的左子樹、根節點的右子樹組成的。

從概念中可以看出，二叉樹定義是遞歸式的，因此后序基本操作中基本都是按照該概念實現的。

2.5.2 二叉樹的遍歷

1.前中后序遍歷
學習二叉樹結構，最簡單的方式就是遍歷。所謂遍歷(Traversal)是指沿著某條搜索路線，依次對樹中每個結點均做一次且僅做一次訪問。訪問結點所做的操作依賴于具體的應用問題(比如：打印節點內容、節點內容加1)。 遍歷是二叉樹上最重要的操作之一，是二叉樹上進行其它運算之基礎。

在遍歷二叉樹時，如果沒有進行某種約定，每個人都按照自己的方式遍歷，得出的結果就比較混亂，如果按照某種規則進行約定，則每個人對于同一棵樹的遍歷結果肯定是相同的。如果N代表根節點，L代表根節點的左子樹，R代表根節點的右子樹，則根據遍歷根節點的先后次序有以下遍歷方式：
NLR：前序遍歷(Preorder Traversal 亦稱先序遍歷)——訪問根結點—>根的左子樹—>根的右子樹。
LNR：中序遍歷(Inorder Traversal)——根的左子樹—>根節點—>根的右子樹。
LRN：后序遍歷(Postorder Traversal)——根的左子樹—>根的右子樹—>根節點。

// 前序遍歷
void preOrder(Node root);// 中序遍歷
void inOrder(Node root);// 后序遍歷
void postOrder(Node root);
比

下面主要分析前序遞歸遍歷，中序與后序圖解類似，同學們可自己動手繪制。

前序遍歷結果：1 2 3 4 5 6
中序遍歷結果：3 2 1 5 4 6
后序遍歷結果：3 1 5 6 4 1
2. 層序遍歷
層序遍歷：除了先序遍歷、中序遍歷、后序遍歷外，還可以對二叉樹進行層序遍歷。設二叉樹的根節點所在層數為1，層序遍歷就是從所在二叉樹的根節點出發，首先訪問第一層的樹根節點，然后從左到右訪問第2層上的節點，接著是第三層的節點，以此類推，自上而下，自左至右逐層訪問樹的結點的過程就是層序遍歷。

【練習】請同學們根據以上二叉樹的三種遍歷方式，給出以下二叉樹的：

選擇題

1. 某完全二叉樹按層次輸出（同一層從左到右）的序列為 ABCDEFGH 。該完全二叉樹的前序序列為()
   A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA
2. 二叉樹的先序遍歷和中序遍歷如下：先序遍歷：EFHIGJK;中序遍歷：HFIEJKG.則二叉樹根結點為()
   A: E B: F C: G D: H
3. 設一課二叉樹的中序遍歷序列：badce，后序遍歷序列：bdeca，則二叉樹前序遍歷序列為()
   A: adbce B: decab C: debac D: abcde
4. 某二叉樹的后序遍歷序列與中序遍歷序列相同，均為 ABCDEF ，則按層次輸出(同一層從左到右)的序列為()
   A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF

【參考答案】 1.A 2.A 3.D 4.A
2.
3.
4.

根據前序和后序能不能創建一棵二又樹呢?
不可以
前序和后序只能確定根的位置

2.5.3 二叉樹的基本操作

// 獲取樹中節點的個數
int size(Node root);// 獲取葉子節點的個數
int getLeafNodeCount(Node root);// 子問題思路-求葉子結點個數// 獲取第K層節點的個數
int getKLevelNodeCount(Node root,int k);// 獲取二叉樹的高度
int getHeight(Node root);// 檢測值為value的元素是否存在
Node find(Node root, int val);//層序遍歷
void levelOrder(Node root);// 判斷一棵樹是不是完全二叉樹
boolean isCompleteTree(Node root)

// 獲取樹中節點的個數
int size(Node root);

// 獲取葉子節點的個數
int getLeafNodeCount(Node root);

// 子問題思路-求葉子結點個數

// 獲取第K層節點的個數
int getKLevelNodeCount(Node root,int k);

// 獲取二叉樹的高度
int getHeight(Node root);

放oj上的話 法二有可能溢出 因為法二計算了2遍 法一直接把當前的記錄下來避免了重復運算造成的算法效率的降低

// 檢測值為value的元素是否存在
Node find(Node root, int val);

//層序遍歷
void levelOrder(Node root);

// 判斷一棵樹是不是完全二叉樹
boolean isCompleteTree(Node root)

2.6 二叉樹相關oj題

1. 相同的樹OJ鏈接
   
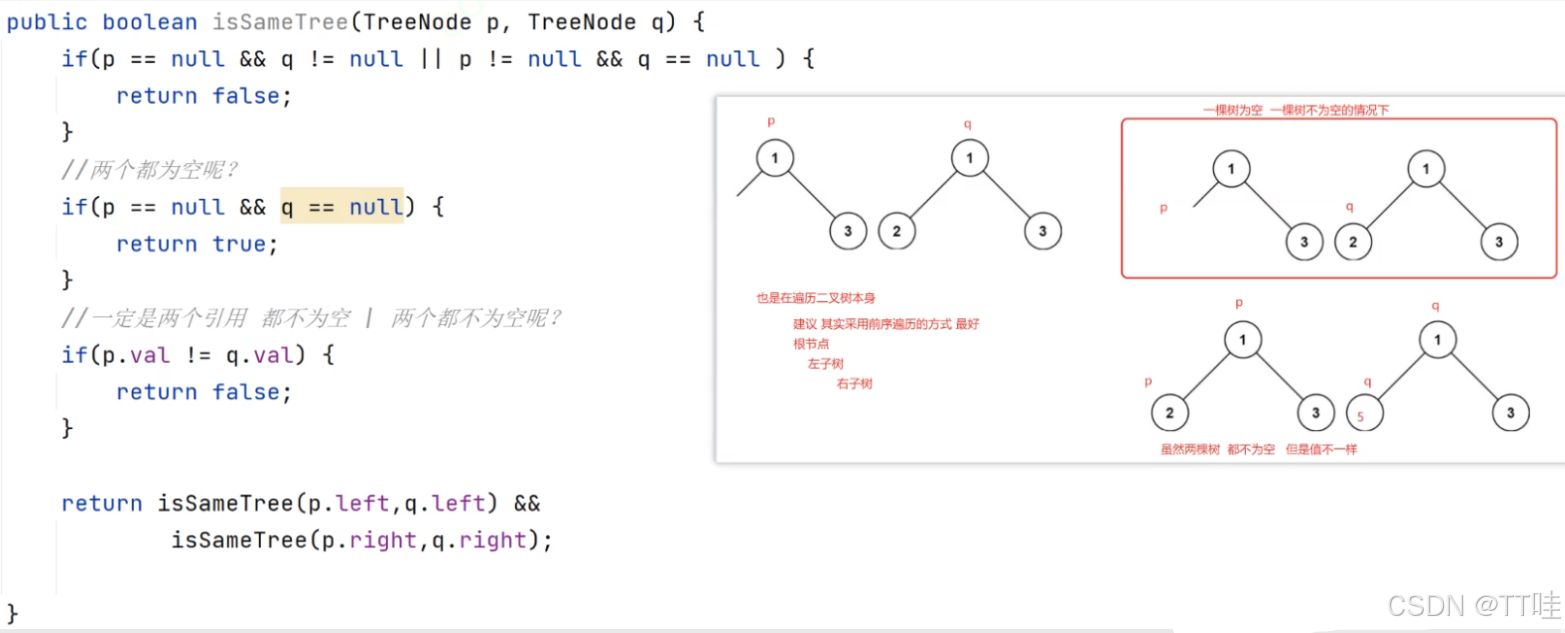
   時間復雜度😮(min(m,n))，其中 m 和n分別是兩個二叉樹的節點數。對兩個二叉樹同時進行深度優先搜索，只有當兩個二叉樹中的對應節點都不為空時才會訪問到該節點，因此被訪問到的節點數不會超過較小的二叉樹的節點數。

/*解題思路：1. 如果兩棵樹都是空，則相同2. 如果兩棵樹一個為空，一個不為空，則不相同3. 如果兩棵樹都不為空，先檢測根是否相同，根如果相同再遞歸檢測兩棵樹的左子樹以及右子樹是否都相同
*/
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {// 兩棵樹都為空，則對稱if(p == null && q == null){return true;}// 如果一棵樹是空，一棵樹不為空，則不對稱if(p == null || q == null){return false;}// 根節點中的值域相等，并且p和q的左右子樹都是對稱的，則對稱，否則不對稱return p.val == q.val &&isSameTree(p.left, q.left) &&isSameTree(p.right, q.right);}
}

2. 另一顆樹的子樹。OJ鏈接
   
   if(root==null)易漏掉 會導致空指針異常

/*解題思路：1. 題目已經說了：空樹是任意一棵樹的子樹2. 如果兩棵樹相同，也可以認為是子樹，因此：只要根節點相同，直接檢測s和t是否為相同的樹即可3. 如果根不相同，檢測t是否為s.left的子樹 或者 s.right的子樹
*/  
class Solution {private boolean isSameTree(TreeNode p, TreeNode q) {// 兩棵樹都為空，則對稱if(p == null && q == null){return true;}// 如果一棵樹是空，一棵樹不為空，則不對稱if(p == null || q == null){return false;}// 根節點中的值域相等，并且p和q的左右子樹都是對稱的，則對稱，否則不對稱return p.val == q.val &&isSameTree(p.left, q.left) &&isSameTree(p.right, q.right);}public boolean isSubtree(TreeNode s, TreeNode t) {// 空樹可以看成是任意一棵樹的子樹if(t == null){return true;}// s為空樹，t不是空樹，則t一定不是s的子樹if(s == null){return false;}// 如果s和t是同一棵樹，則t是s的子樹if(isSameTree(s, t)){return true;}// 否則： 檢測t是否為s左子樹的子樹，或者是否為s右子樹的子樹return isSubtree(s.left, t) || isSubtree(s.right, t);}
}

3. 翻轉二叉樹。OJ鏈接
   

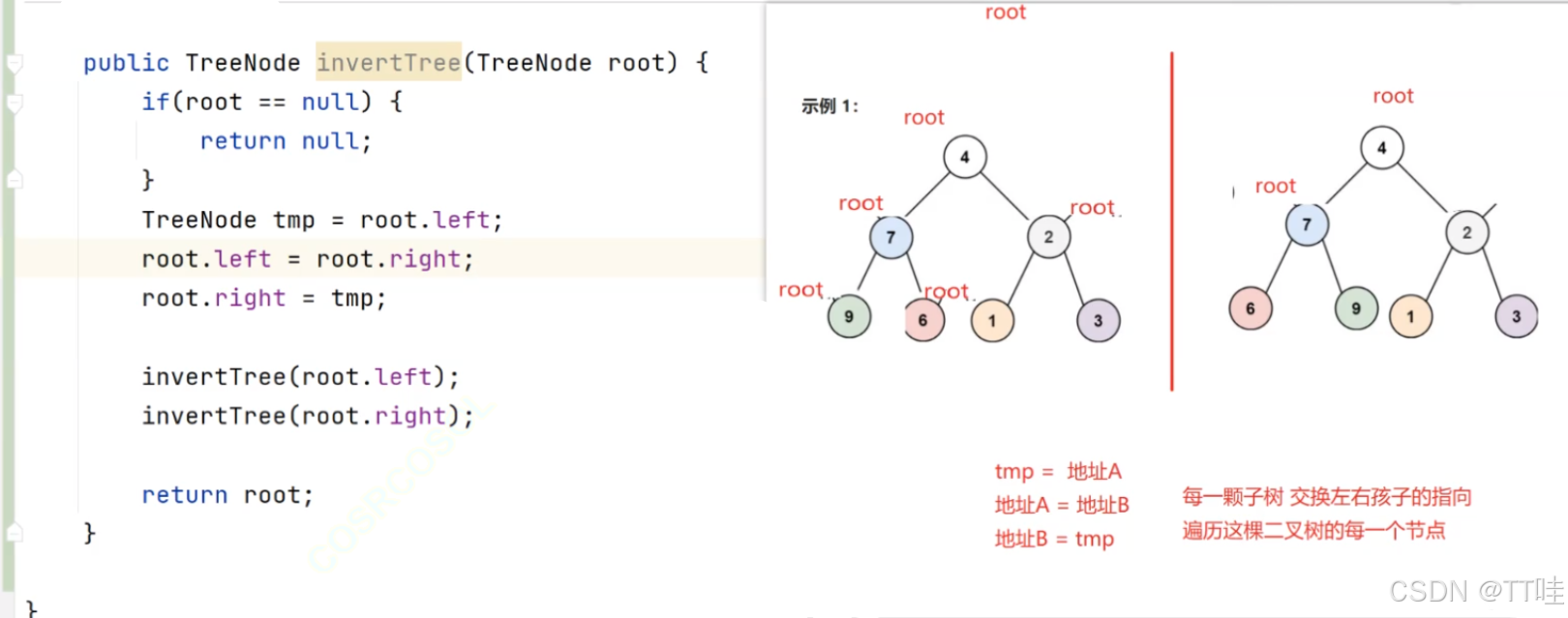
/*解題思路：二叉樹前序遍歷規則應用如果樹不空時：1. 交換根的左右子樹2. 遞歸反轉根的左子樹3. 遞歸反轉根的右子樹
*/  
class Solution {public TreeNode invertTree(TreeNode root) {if(null != root){// 交換根的左右子樹TreeNode tmp = root.left;root.left = root.right;root.right = tmp;// 遞歸反轉根的左子樹invertTree(root.left);// 遞歸反轉根的右子樹invertTree(root.right);}return root;}
}

4. 平衡二叉樹OJ鏈接
   可以在求樹高度的過程中判斷樹是否平衡
   
   上面代碼leftHeight >= 0 && rightHeight >= 0 的關鍵作用
   核心邏輯：確保了：
   1.左右子樹自身是平衡的（返回有效高度）。
   2.只有在子樹平衡的前提下，才檢查高度差是否合法。
   若省略：僅依賴高度差判斷，會漏掉子樹自身不平衡的情況，導致錯誤結果。
   新解題思路：
   平衡二叉樹的概念：二叉樹中每個節點左右子樹高度差的絕對值不能超過1
   根據概念來檢測：
   1. 如果是空樹，直接返回，注意：空樹也是平衡二叉樹
   2. 求根的左右子樹高度，然后做差檢測其高度差的絕對值是否超過1 如果超過則不是
   3. 遞歸檢測根的左右子樹是否為平衡二叉樹

class Solution {public int GetHeight(TreeNode root){if(root == null){return 0;}int leftHeight = GetHeight(root.left);int rightHeight = GetHeight(root.right);return Math.max(leftHeight,rightHeight)+1;}public boolean isBalanced(TreeNode root) {// 空樹是平衡二叉樹if(root == null){return true;}// 獲取root左右子樹的高度int leftHeight = GetHeight(root.left);int rightHeight = GetHeight(root.right);// 根據平衡樹的概念，檢測root節點的平衡性if(Math.abs(rightHeight - leftHeight) > 1){return false;}// 通過遞歸方式：檢測root的左右子樹是否為平衡樹return isBalanced(root.left) && isBalanced(root.right);}
}

5. 對稱二叉樹。OJ鏈接
   
   解題思路：直接遞歸檢測root的左右是否對稱即可
   1. 如果兩棵樹都是空樹，則對稱
   2. 如果兩棵樹一棵為空樹，一棵不為空樹，則一定不是對稱樹
   3. 如果兩棵樹都不為空，先檢測兩棵樹的root是否相同，如果相同，再檢測一個的left是否為另一個的right 并且一個的right是否為另一個的left

class Solution {public boolean isSymmetric(TreeNode root) {if(null == root)return true;            return isSymmetric(root.left, root.right);}private boolean isSymmetric(TreeNode left, TreeNode right){if(null == left && null == right){return true;}if(null == left || null == right){return false;}// 此處保證了兩顆樹都是存在的return left.val == right.val &&isSymmetric(left.left, right.right) &&isSymmetric(left.right, right.left);}
}

6. 二叉樹的構建及遍歷。OJ鏈接
   
   
   注意：public static int i最好把static去掉 否則當有多個測試用例時 i無法重新為0

/*注意在線OJ算法題分為兩種類型：1. 接口類型OJ：此種OJ題目是方法名字已經給好，用戶直接寫代碼即可，也不需要包含什么包2. IO類型的OJ：此種OJ題目需要用戶定義一個public的Main類，然后在Main類中提供一個main方法，在main方法中完成事情，中間如要需要用到其他集合類，必須手動  導入包在線OJ中的循環輸入，輸入單個值怎么循環接收，整行值怎么循環接收
解題思路：參考課堂將的二叉樹的創建以及遍歷
*/
import java.util.*;
public class Main{// 二叉樹的節點進行定義public static class TreeNode{char value;TreeNode left;TreeNode right;        public TreeNode( char value){this.value = value;}}    // 指向二叉樹的根節點TreeNode root;int index;void createBinaryTree(String preStr, char invalid){index = 0;root = createBinaryTreeN(preStr, invalid);}   TreeNode createBinaryTreeN(String preStr, char invalid){TreeNode treeRoot = null;if(index < preStr.length() && preStr.charAt(index) != invalid){// 創建根節點treeRoot = new TreeNode(preStr.charAt(index));           // 創建根節點的左子樹++index;treeRoot.left = createBinaryTreeN(preStr, invalid);            // 創建根節點的右子樹++index;treeRoot.right = createBinaryTreeN(preStr, invalid);}        return treeRoot;}    public void InOrder(){InOrder(root);System.out.println();}    private void InOrder(TreeNode treeRoot){if(treeRoot != null){InOrder(treeRoot.left);System.out.print(treeRoot.value + " ");InOrder(treeRoot.right);}}  public static void main(String[] args){Scanner scaner = new Scanner(System.in);      while(scaner.hasNext()){            // 接收前序遍歷的結果String str = scaner.nextLine();            Main tree = new Main();tree.createBinaryTree(str, '#');tree.InOrder();}}
}

7. 二叉樹的分層遍歷 。OJ鏈接
   層序遍歷如下：
   
   但此題要求返回List<List < Integer > >
   代碼應更新如下:
   
   
8. 給定一個二叉樹, 找到該樹中兩個指定節點的最近公共祖先 。OJ鏈接
   法一：
   
   
   法二：
   
   
   
   
   
   
9. 根據一棵樹的前序遍歷與中序遍歷構造二叉樹。 OJ鏈接
   
   
   
   注意：priIndex不能用局部變量 要寫成成員變量
10. 根據一棵樹的中序遍歷與后序遍歷構造二叉樹OJ鏈接
    
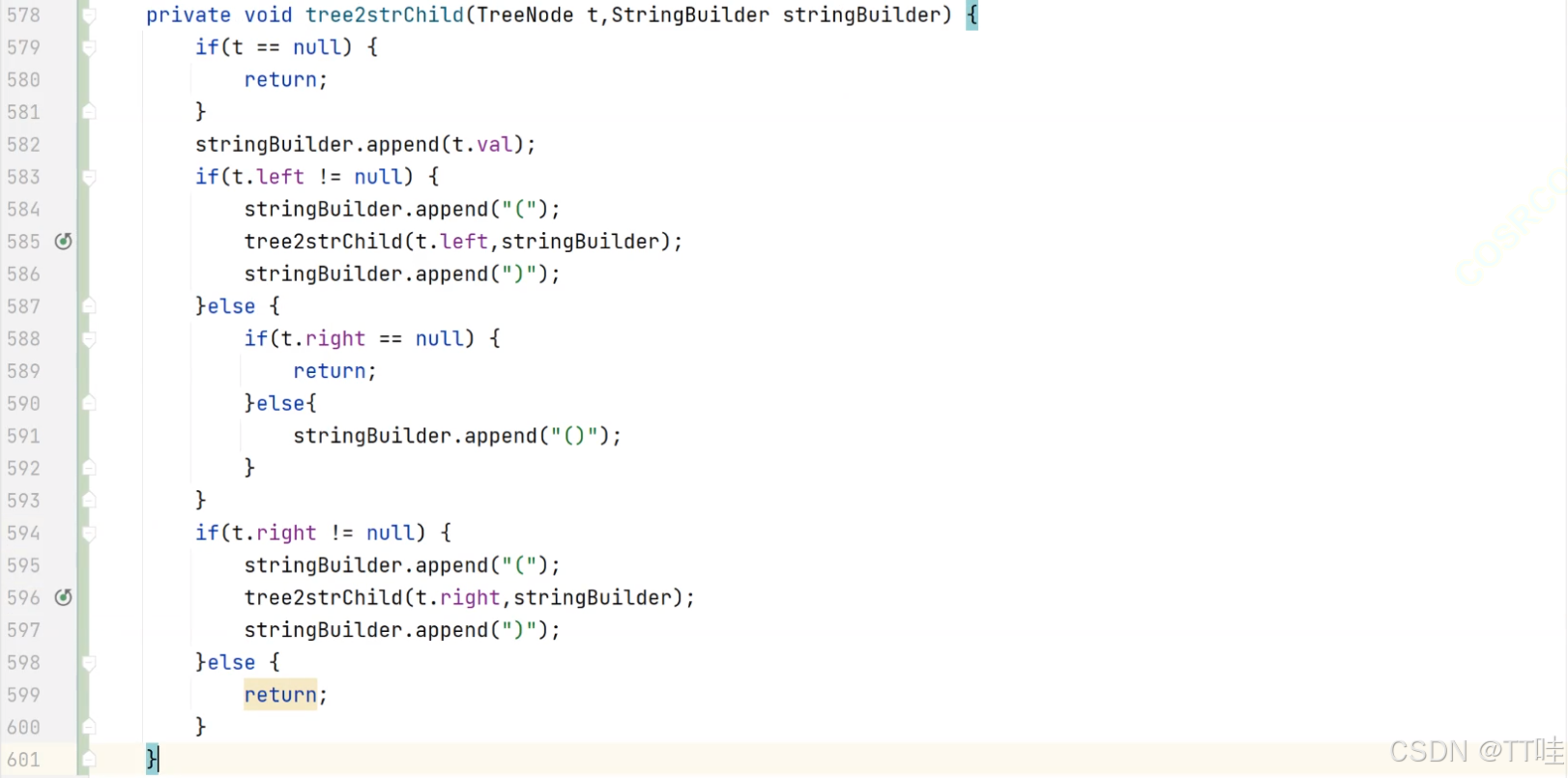
11. 二叉樹創建字符串。OJ鏈接
    
    
    
12. 二叉樹前序非遞歸遍歷實現 。OJ鏈接 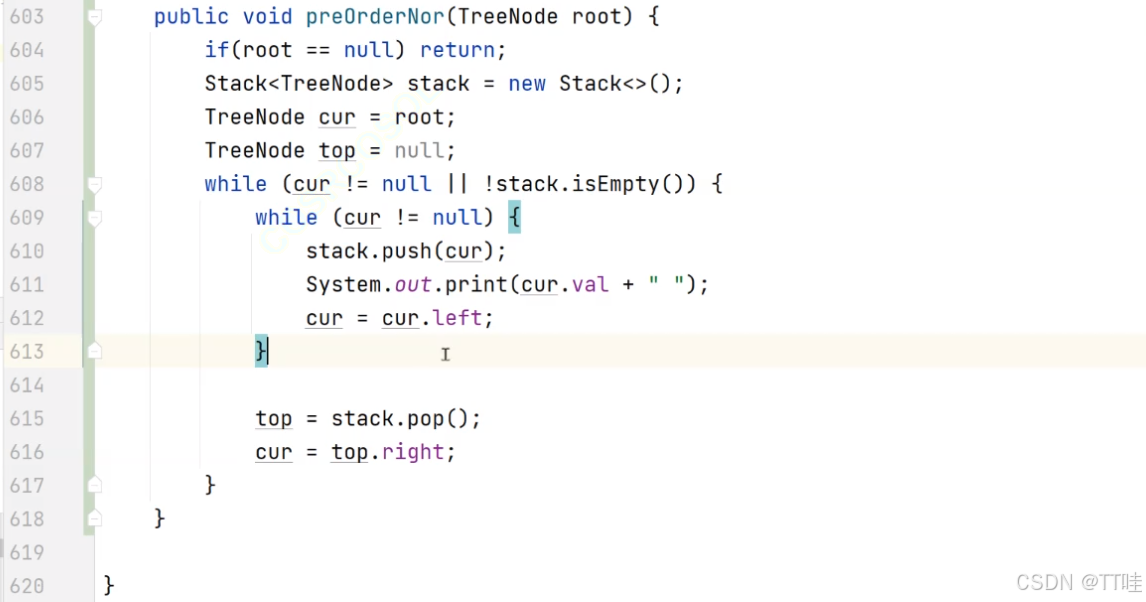遞歸：
13. 二叉樹中序非遞歸遍歷實現。OJ鏈接
    
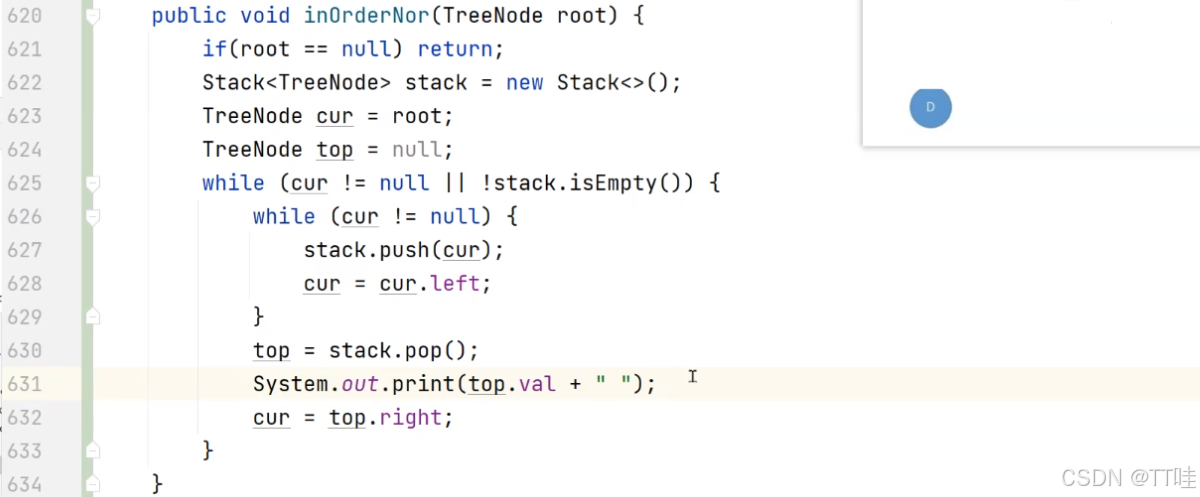
    遞歸：
    
14. 二叉樹后序非遞歸遍歷實現。OJ鏈接
    
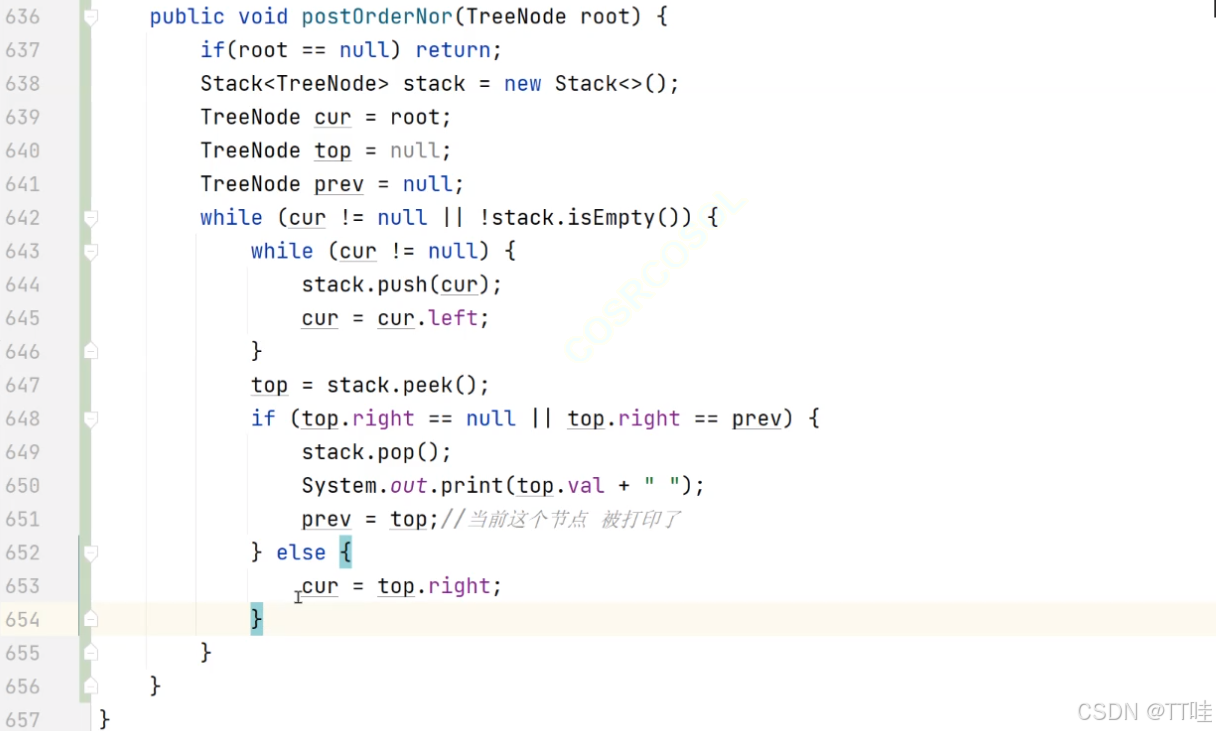
    遞歸：