在MySQL中，無論是Innodb還是MyIsam，都使用了B+樹作索引結構(這里不考慮hash等其他索引)。本文將從最普通的二叉查找樹開始，逐步說明各種樹解決的問題以及面臨的新問題，從而說明MySQL為什么選擇B+樹作為索引結構。

一、二叉查找樹(BST)：不平衡

二叉查找樹(BST，Binary Search Tree)，也叫二叉排序樹，在二叉樹的基礎上需要滿足：任意節點的左子樹上所有節點值不大于根節點的值，任意節點的右子樹上所有節點值不小于根節點的值。如下是一棵BST

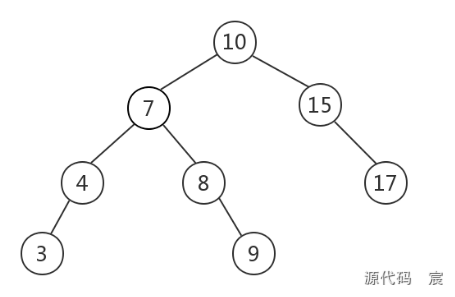
當需要快速查找時，將數據存儲在BST是一種常見的選擇，因為此時查詢時間取決于樹高，平均時間復雜度是O(lgn)。然而，BST可能長歪而變得不平衡，如下圖所示，此時BST退化為鏈表，時間復雜度退化為O(n)。

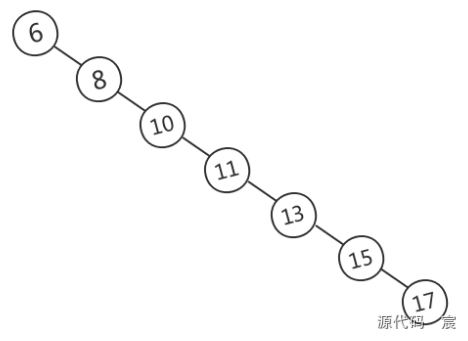
為了解決這個問題，引入了平衡二叉樹。

二、平衡二叉樹(AVL)：旋轉耗時

AVL樹是嚴格的平衡二叉樹，所有節點的左右子樹高度差不能超過1；AVL樹查找、插入和刪除在平均和最壞情況下都是O(lgn)。

AVL實現平衡的關鍵在于旋轉操作：插入和刪除可能破壞二叉樹的平衡，此時需要通過一次或多次樹旋轉來重新平衡這個樹。 當插入數據時，最多只需要1次旋轉(單旋轉或雙旋轉)；但是當刪除數據時，會導致樹失衡，AVL需要維護從被刪除節點到根節點這條路徑上所有節點的平衡，旋轉的量級為O(lgn)。

由于旋轉的耗時，AVL樹在刪除數據時效率很低；在刪除操作較多時，維護平衡所需的代價可能高于其帶來的好處，因此AVL實際使用并不廣泛。

三、紅黑樹：樹太高

與AVL樹相比，紅黑樹并不追求嚴格的平衡，而是大致的平衡：只是確保從根到葉子的最長的可能路徑不多于最短的可能路徑的兩倍長。從實現來看，紅黑樹最大的特點是每個節點都屬于兩種顏色(紅色或黑色)之一，且節點顏色的劃分需要滿足特定的規則(具體規則略)。紅黑樹示例如下：

對紅黑樹不了解的可以看紅黑樹的創建

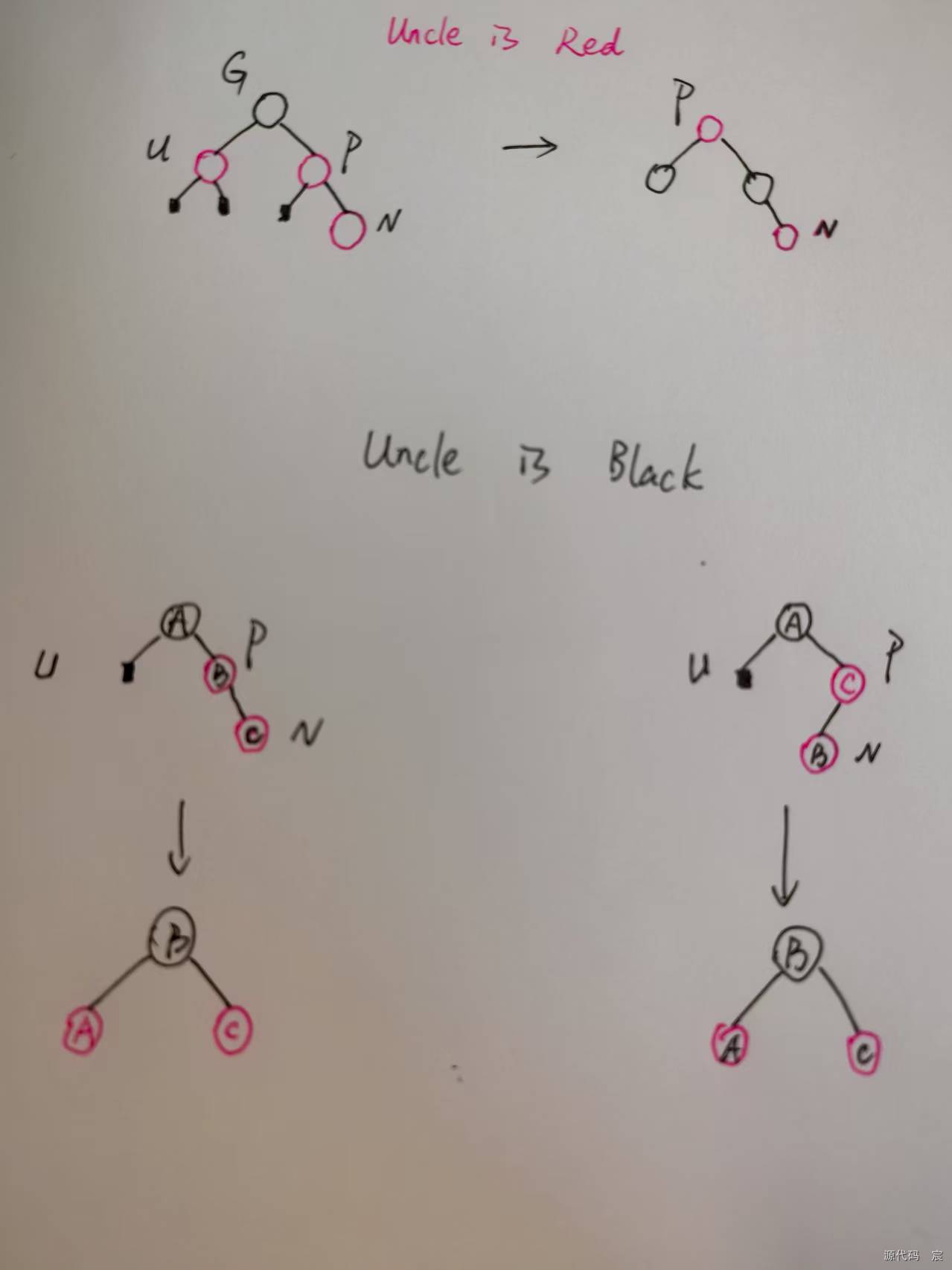
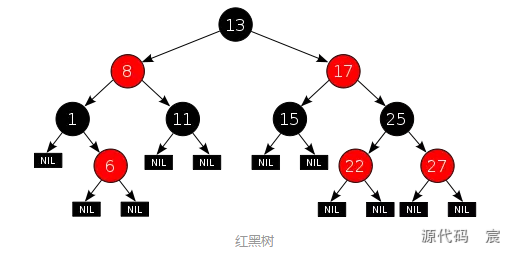
與AVL樹相比，紅黑樹的查詢效率會有所下降，這是因為樹的平衡性變差，高度更高。但紅黑樹的刪除效率大大提高了，因為紅黑樹同時引入了顏色，當插入或刪除數據時，只需要進行O(1)次數的旋轉以及變色就能保證基本的平衡，不需要像AVL樹進行O(lgn)次數的旋轉。 總的來說，紅黑樹的統計性能高于AVL。

因此，在實際應用中，AVL樹的使用相對較少，而紅黑樹的使用非常廣泛。例如，C++中的map使用紅黑樹存儲排序鍵值對

對于數據在內存中的情況，紅黑樹的表現是非常優異的。但是對于數據在磁盤等輔助存儲設備中的情況（如MySQL等數據庫），紅黑樹并不擅長，因為紅黑樹長得還是太高了。當數據在磁盤中時，磁盤IO會成為最大的性能瓶頸，設計的目標應該是盡量減少IO次數；而樹的高度越高，增刪改查所需要的IO次數也越多，會嚴重影響性能。

由一個例子總結索引的特點

加索引是數據庫加速查詢的一種方式，那么為什么用索引可以加快查詢呢？

講到索引，其實我們經常會聽到一個圖書館的例子，圖書館里的書目繁雜，我們如何從若干本書里面找到一本我們想要的書呢？

我們根據圖書館系統檢索，可以找到某本書對應的圖書編號。

在基于書籍按照一定規則排列的前提下，我們可以根據圖書編號找到這本書。

例如，假設圖書編號根據：

第幾個書架 - 書架上第幾個格子 - 從左到右數第幾個位置

這樣的規則編排，

我們就可以輕松的獲取到我們想要的書籍。

你也許發現了，這個例子中，藏著兩個信息：

基于哈希表實現的哈希索引

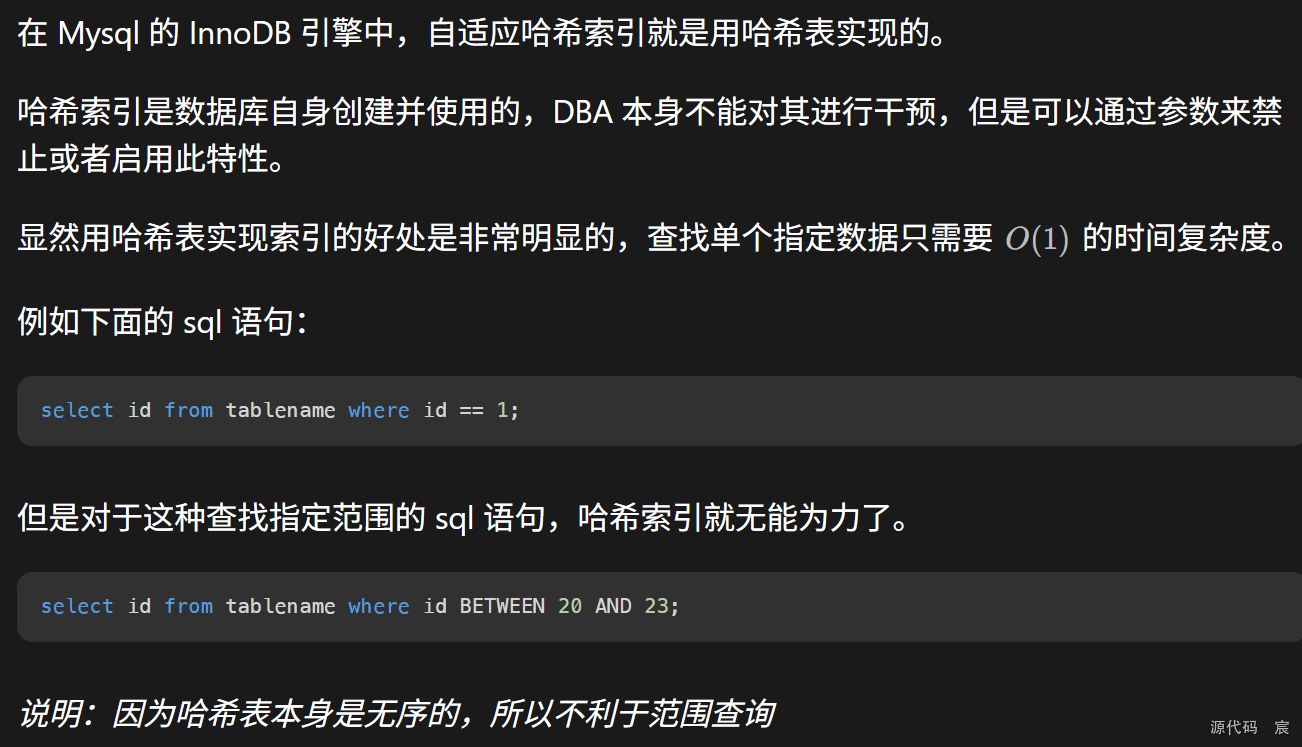
到這里我們遇到了一個問題，就是哈希表雖然從查找效率上滿足了我們查找單個數據的要求，但是顯然，當遇到范圍查詢時，由于哈希表本身的無序性，不利于指定范圍查找。

也就是說，我們的需求增加了，我們希望數據的組織方式，既要有一定規則，又要有序。

在引出這種數據結構之前，我們首先來看一種查找方式：二分查找。

高效的查找方式：二分查找

二分查找的核心思想是給定一個 有序 的數組，在查找過程中采用跳躍式的方式查找，即先以有序數列的中點位置為比較對象，如果要查找的元素小于中點元素，則將待查序列縮小為左半部分，否則為右半部分。通過每次比較，將查找區間減少一半，直到找到所需元素。

基于二分查找思想的二叉查找樹

二叉查找樹（Binary Search Tree）即BST樹是這樣的一種數據結構,如下圖：


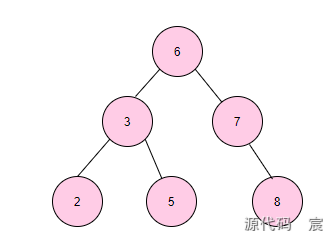
但是當二叉樹的構造變成這樣時,

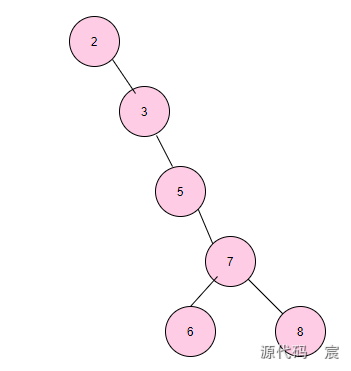
此時我們再查找 8 時,查找效率就淪為接近順序遍歷查找的效率。

顯然這不是我們想要的，二叉查找樹也需要 balance。

由于樹是存儲在磁盤中的，訪問每個節點，都對應一次磁盤 I/O 操作（假設一個節點的大小「小于」操作系統的最小讀寫單位塊的大小），也就是說樹的高度就等于每次查詢數據時磁盤 IO 操作的次數，所以樹的高度越高，就會影響查詢性能。 二叉查找樹由于存在退化成鏈表的可能性，會使得查詢操作的時間復雜度從 O(logn) 升為 O(n)。

升級版的BST樹：AVL 樹

我們對二叉查找樹做個限制，限制必須滿足任何節點的兩個子樹的最大差為 1，也是AVL 樹的定義，這樣我們的查找效率就有了一定的保障。

AVL 樹 是一種自平衡二叉查找樹(self-balancing binary search tree)。

當然，維護AVL 樹也是需要一定開銷的，即當樹插入/更新/刪除新的數據時假設破壞了樹的平衡性，那么需要通過左旋和右旋來維護樹的平衡。

當數據量很多時，同樣也會出現二叉樹過高的情況。

我們知道AVL 樹的查找效率為 O(log n)，也就是說，當樹過高時，查找效率會下降。

另外由于我們的索引文件并不小，所以是存儲在磁盤上的。文件系統需要從磁盤讀取數據時，一般以頁為單位進行讀取，假設一個頁內的數據過少，
那么操作系統就需要讀取更多的頁，涉及磁盤隨機 I/O 訪問的次數就更多。

將數據從磁盤讀入內存涉及隨機 I/O 的訪問，是數據庫里面成本最高的操作之一。

因而這種樹高會隨數據量增多急劇增加，每次更新數據又需要通過左旋和右旋維護平衡的二叉樹，不太適合用于存儲在磁盤上的索引文件。

四、B樹：為磁盤而生

前面我們看到，雖然AVL樹既有鏈表的快速插入與刪除操作的特點，又有數組快速查找的優勢，但是這并不是最符合磁盤讀寫特征的數據結構。

也就是說，我們要找到這樣一種數據結構，能夠有效的控制樹高，那么我們把二叉樹變成m叉樹，也就是下圖的這種數據結構:B 樹。

B樹是一種這樣的數據結構：





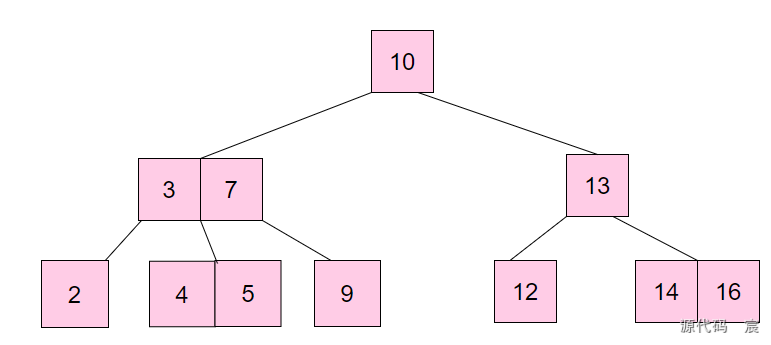
可以看到，B樹在保留二叉樹預劃分范圍從而提升查詢效率的思想的前提下，做了以下優化：

二叉樹變成 m 叉樹，這個 m 的大小可以根據單個頁的大小做對應調整，從而使得一個頁可以存儲更多的數據，從磁盤中讀取一個頁可以讀到的數據就更多，隨機 IO 次數變少，大大提升效率。

但是我們看到，我們只能通過中序遍歷查詢全表，當進行范圍查詢時，可能會需要中序回溯。

讓我們從空的5階B-Tree開始，按照順序插入這些數字：3, 8, 31, 11, 23, 29, 50, 28, 1, 2。

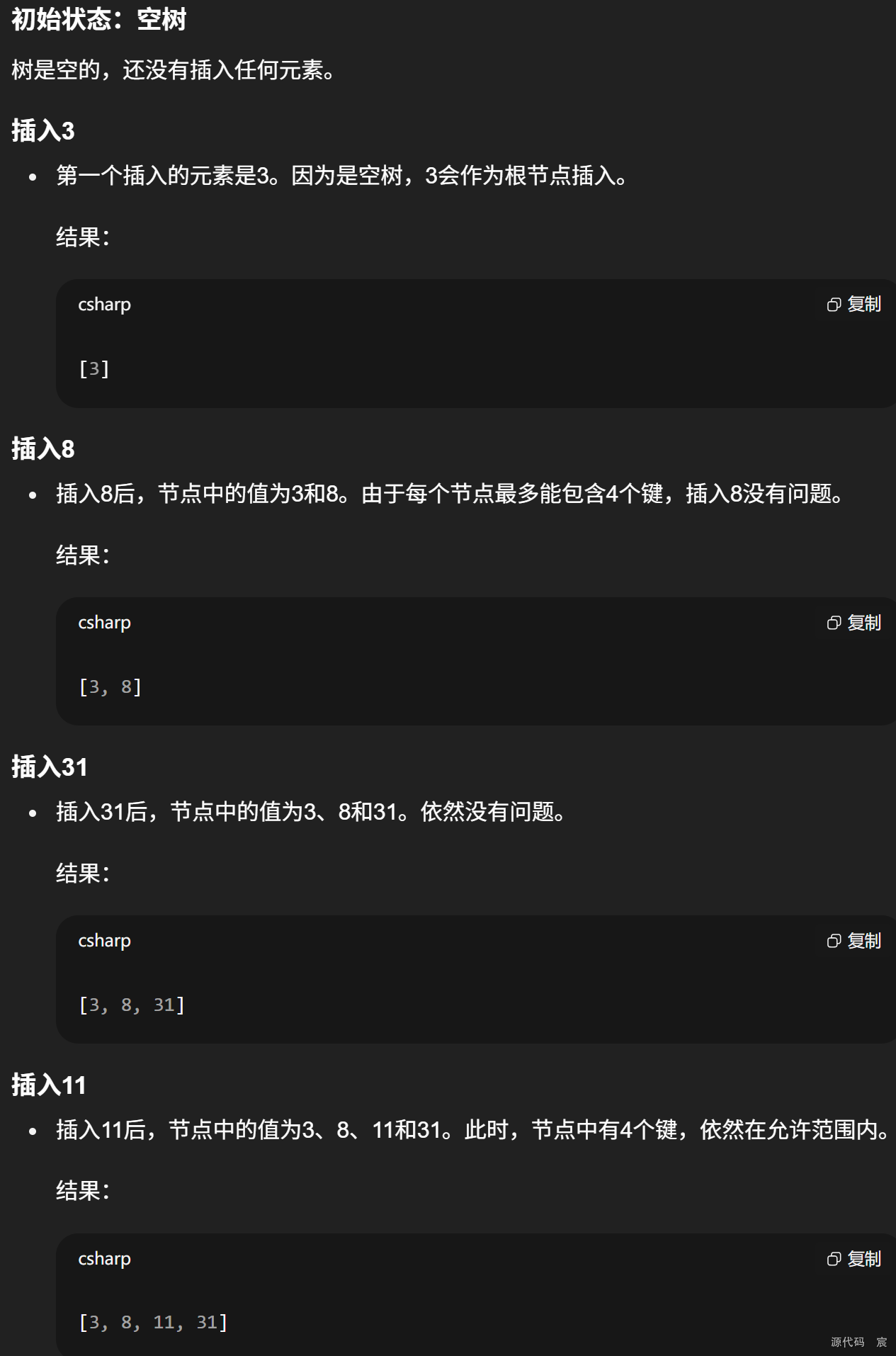
對于5階的B樹每個結點最多存儲4個key，所以對于3，8，31，11的新增(排序)很好理解

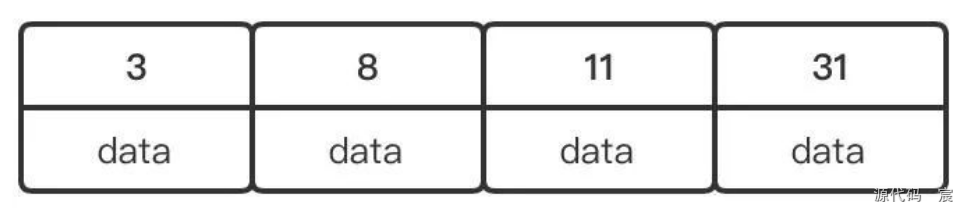
但是當我們新增23的時候，就會打破這種規則，所以我們需要對結點進行分裂，來保證定義2成立，分裂操作很簡單， 將中間元素進行提取，充當父結點，左右元素一分為2，分別充當孩子結點。

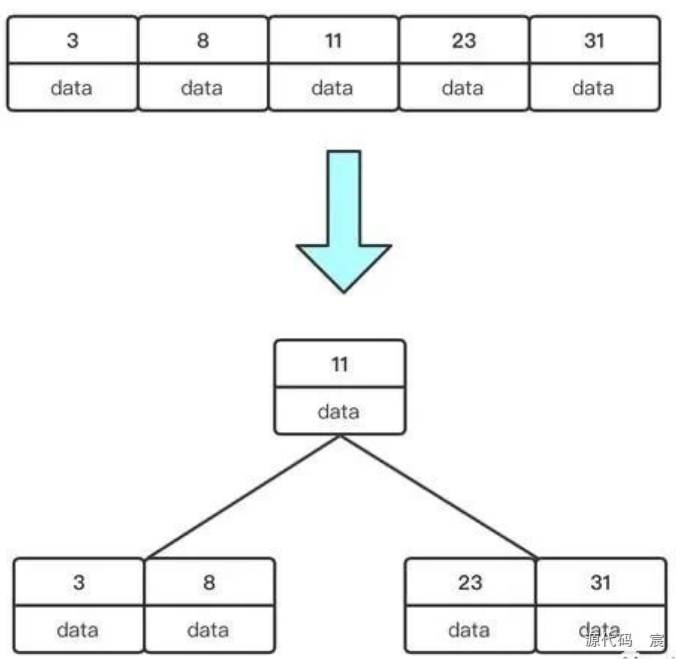
我們繼續新增29，50

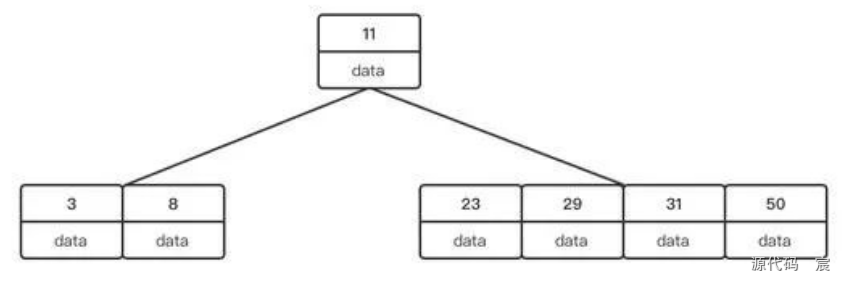
新增到28的時候，又會出現分裂的動作，但是與第一次分裂不同，這個時候分裂出來的中間結點需要進行上升，然后左右元素，與父級上升的結點進行關聯， 這樣才能保證定義5成立:根結點到每個葉子結點的長度都相同

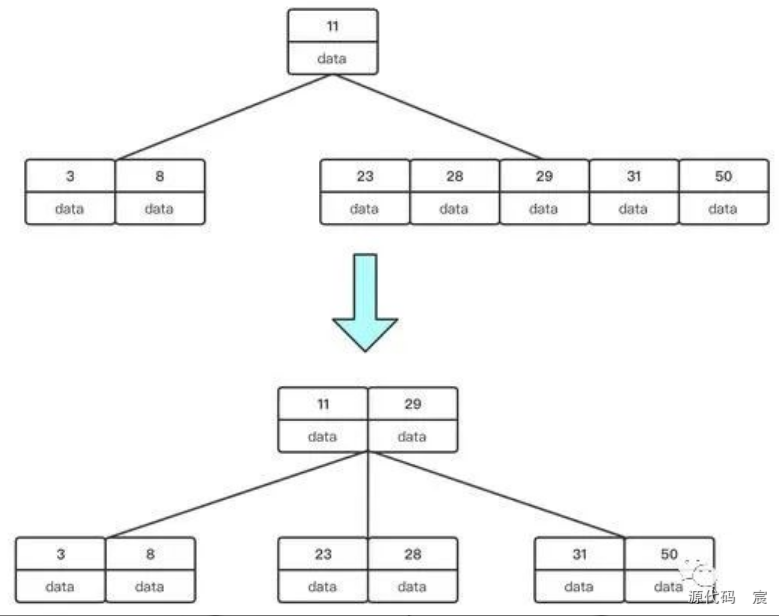
繼續新增1，2

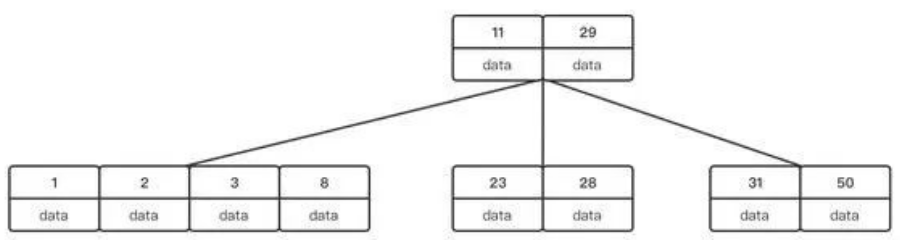
到這里就新增完成了，可以發現為了保證關鍵字不超過m-1,需要進行分裂，而分裂的操作需要保證根結點到任意葉子結點距離是相等的

刪除操作

相對于新增操作，刪除操作比新增要復雜一些，因為新增只涉及到分裂，但是刪除會涉及到替換結點，借結點，合并結點等操作。這些操作的目的同樣是為了保證結構滿足定義

首先看替換結點，當我們要刪除非葉子結點的時候，比如圖上的29，我們使用它的前繼或者后繼的結點來替換它，這里前繼/后繼指的是， 中序遍歷結果的前一個/后一個結點，而且在B樹中，該結點必然是葉子結點，比如29的前繼結點是28，后繼結點是31。

當上面替換成功之后，我們就要把當前的葉子結點刪掉，刪除動作很簡單，但是 當我們把關鍵字刪掉之后，需要判斷當前結點的關鍵字是否滿足我們所說的至少有Math.ceil(m/2)-1個的要求，如果滿足，刪除成功，不滿足時為了保證 滿足這樣的條件，我們看看兄弟結點有沒有富裕(大于Math.ceil(m/2)-1)的關鍵字，給他借過來。這一步叫借結點。

那么合并結點就是當兄弟結點不足的時候，我們需要找兄弟結點來進行合并，從而滿足B樹的定義。

下面具體看下實現過程:
首先我們刪除關鍵字8：因為是葉子結點，且刪除后關鍵字滿足 >=Math.ceil(m/2)-1 的條件

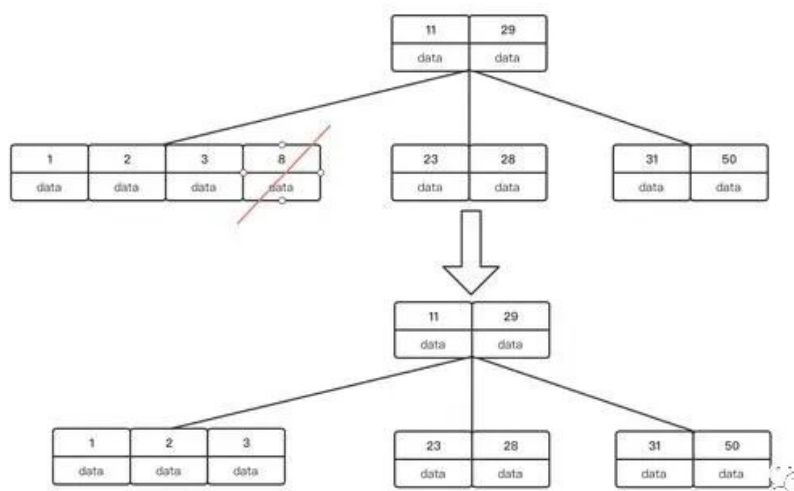
我們繼續刪除關鍵字29：首先找到他的前繼結點關鍵字28來替換刪除

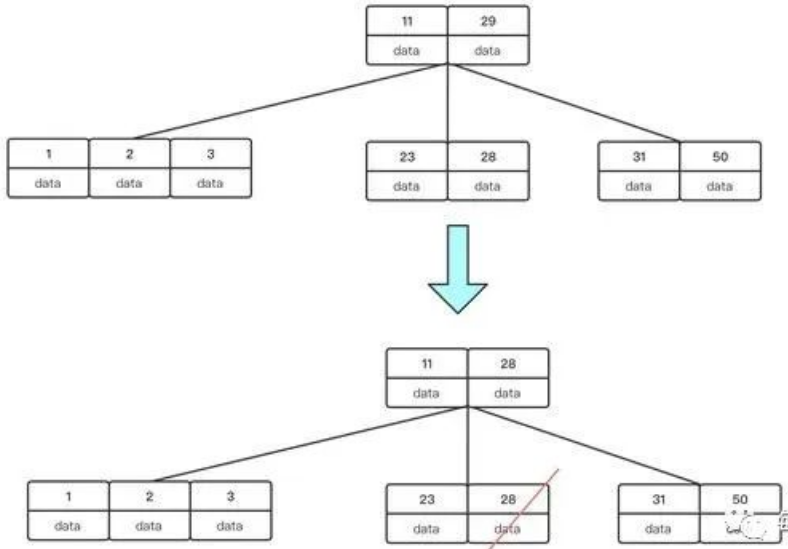
刪除之后我們會發現當前結點關鍵字已經不足2了，所以需要借結點或者合并結點，我們會發現，左兄弟結點是富裕的，所以可以向左兄弟結點借關鍵字。借的過程：父結點下移一個關鍵字，左兄弟結點上移一個關鍵字，從而使B樹平衡。

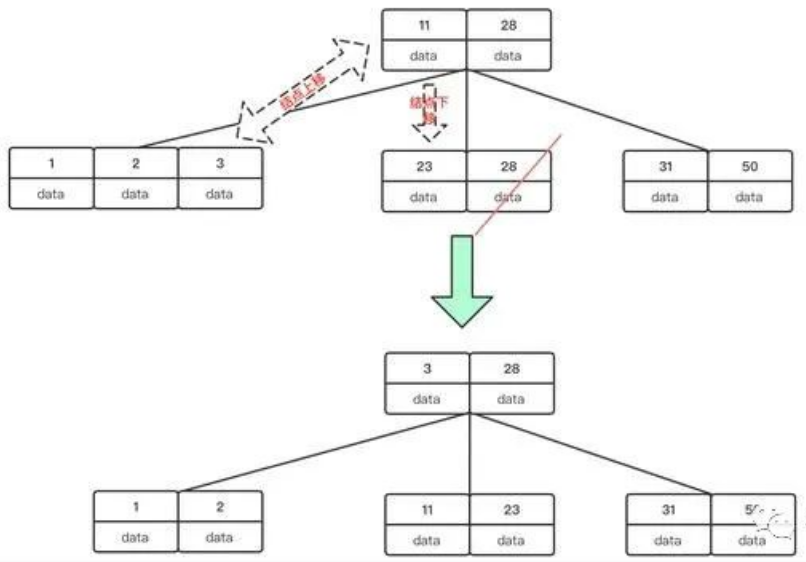
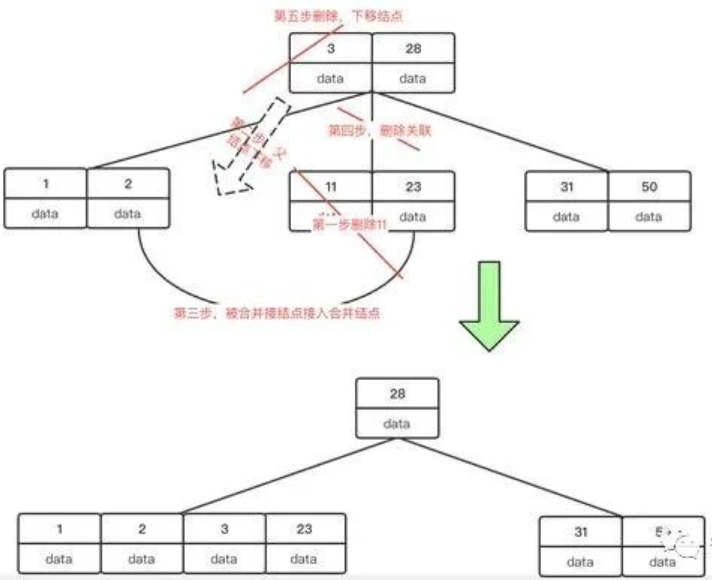
刪完29之后，我們再來刪除關鍵字11，此時兄弟結點沒有富裕的關鍵字來讓該結點滿足 >=Math.ceil(m/2)-1 的條件，所以需要進行結點合并， 這里我們選擇合并左孩子來進行合并，合并過程：將父結點關鍵字下移，到合并結點，失衡的被合并結點關鍵字插入到合并結點，父結點刪除失衡結點。由于父結點是根結點，所以即使一個關鍵字也符合要求。

總結

在實現B樹的過程中，有一點容易讓人誤解的是孩子結點與父親結點的關系，實際上孩子是整個結點的孩子，而不是結點某個關鍵字的孩子。

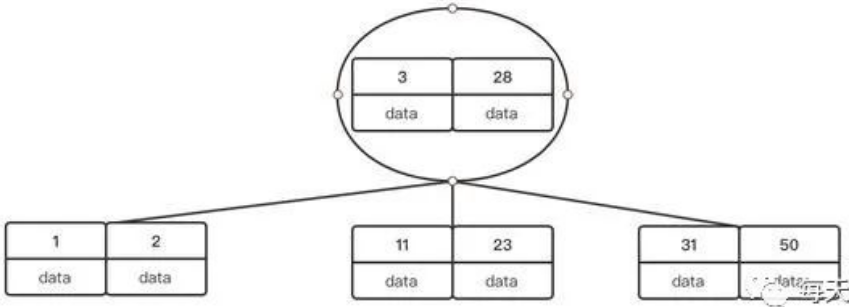
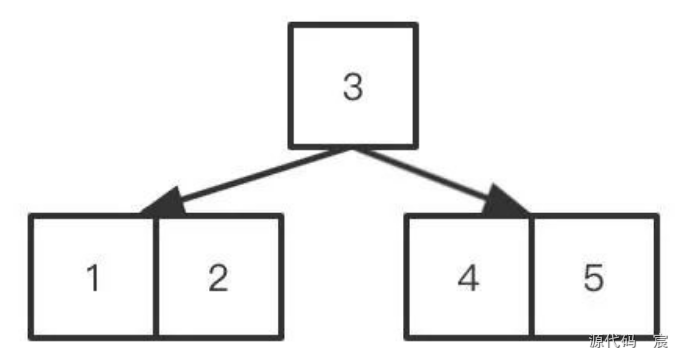
但是孩子結點與父親結點關鍵字之間是存在一定的關系的，比如父結點有兩個關鍵字，那么就會有三個孩子，而父結點關鍵字所在的索引序號，比如下標是0， 那么孩子中下標為0的結點所有關鍵字都會小于父親結點下標為0的關鍵字，如下圖，這也是為什么使用二分可以找到相應關鍵字的原因。

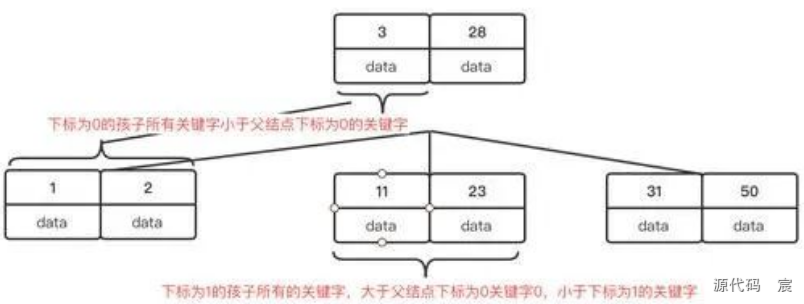
下圖是一個3階B樹的例子

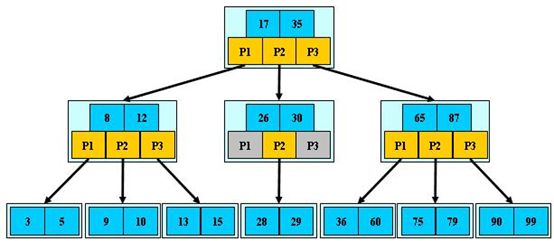
B樹的優勢除了樹矮小，還有對訪問局部性原理的利用。所謂局部性原理，是指當一個數據被使用時，其附近的數據有較大概率在短時間內被使用。B樹將鍵相近的數據存儲在同一個節點，當訪問其中某個數據時，數據庫會將該整個節點讀到緩存中；當它臨近的數據緊接著被訪問時，可以直接在緩存中讀取，無需進行磁盤IO；換句話說，B樹的緩存命中率更高。

B樹在數據庫中有一些應用，如mongodb的索引使用了B樹結構。但是在很多數據庫應用中，使用了是B樹的變種B+樹。

五、B+樹

基于以上的缺陷，又誕生了一種新的優化B樹的樹: B+ 樹

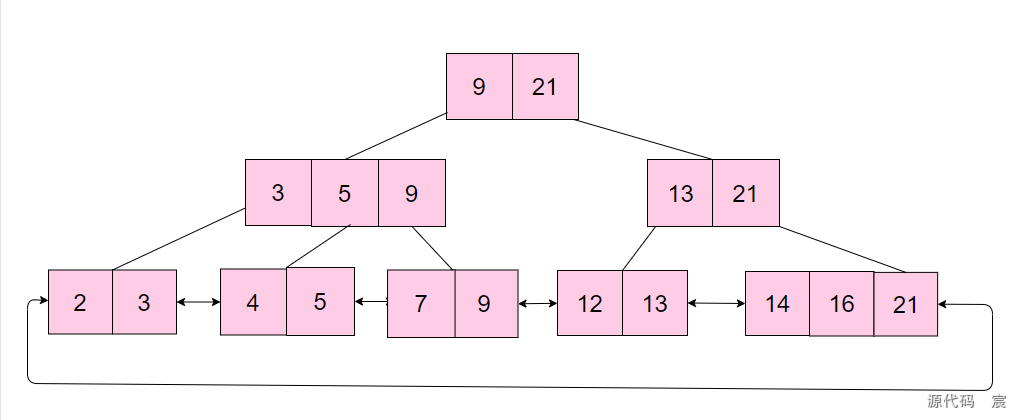
B+樹在定義上似乎沒有官方的定義，從論壇上看，目前還是對定義存在兩點爭論:
其一：B+Tree是否B-Tree一樣是結點有M-1個關鍵字擁有M棵子樹，還是M個關鍵字擁有M顆子樹。
其二：內部結點的索引值使用最大值還是最小值。

不過上述的爭論對于實現并沒有大的影響，我們可以自己去定義。所以這里選用百度百科上對B+樹的描述:
(1)每個結點至多有m個子女；
(2)除根結點外，每個結點至少有[m/2]個子女，根結點至少有兩個子女；
(3)有k個子女的結點必有k個關鍵字。

下面是實現的樹(貌似根結點可以有一個關鍵字，但是這里還是引用k個子女的結點必有k個關鍵字 這條邏輯)。

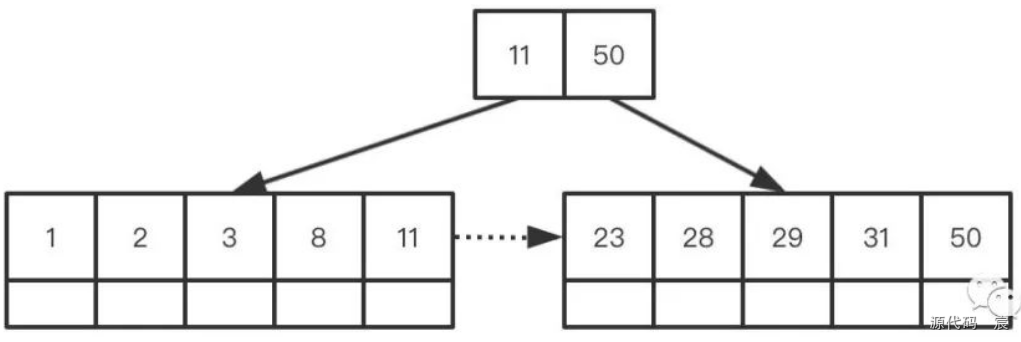
從上面B+樹的圖可以看出與B-樹相比，非葉子結點不存儲數據，僅充當索引結點，其次是所有的數據都存儲在葉子結點上， 且葉子結點利用指針形成單鏈表（雙向鏈表，筆誤）。通過這些特征我們可以得知：

• 1.由于B+樹內部結點不存儲數據，所以樹更加矮，內部結點在相同大小的磁盤頁能存儲更多，一次性讀入內存的關鍵字也會更多，減少IO操作。
• 2.由于B+樹內部結點不存儲數據，所以查詢全部落入葉子結點，所以相對B樹查詢更加穩定，
• 3.由于B+樹葉子結點使用指針鏈接成鏈表，所以相對與B-樹，其范圍查詢更加高效，因為B-樹中范圍查詢 需要對B-樹進行中序遍歷，所以效率會低。

注:B-Tree穩定不代表一定會快，如果是隨機訪問或者單一查詢，有可能B樹更快(數據存儲在距離根結點越近則越快)， 同理IO操作也不一定比B+Tree多。這也是為什么非關系型數據庫不選用B+Tree的原因，因為非關系型數據庫通常都是單一查詢， 不需要遍歷匹配。還需要注意的是，B+Tree與B-Tree一樣，當按照key值的大小順序插入分裂時，每個葉子結點的存儲效率只有50%，如下圖，我們會發現2與3之間不能再插入其他的正整數， 也就造成了空間的浪費

構建B+樹

仍以5階為例，來構建5階B+樹。通過B+樹的定義，我們可以知道，其結點最多有5個關鍵字，最少有[5/2]=3個關鍵字。這里假設存儲的關鍵字為3, 8, 31, 11, 23, 29, 50, 28,1, 2，來看如何構建。

首先定義一顆空樹，然后依次新增，新增流程如下：依次插入3, 8, 31, 11, 23

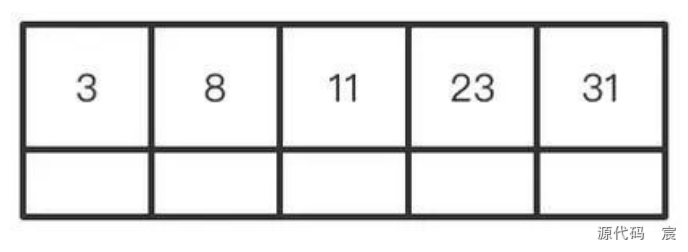
此時結點關鍵字已經達到M個的要求，如果再繼續新增29時，會同B樹一樣，需要進行分裂。但是與B樹分裂存在一些區別， 如下圖，關鍵字上升的過程中，關鍵字并未從原來的結點中移除(B樹中會被移除)，其次根結點形成時，上升了兩個關鍵字， 來保證k個子女的結點必有k個關鍵字的要求(我見到也有根結點有一個關鍵字的博文，這里感覺不打緊，所以就不糾結)， 最后就是葉子結點之間利用形成單向鏈表

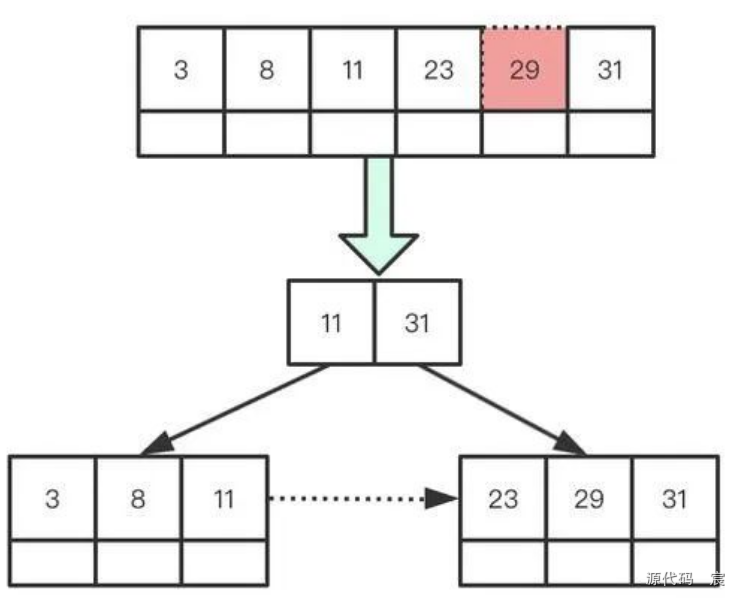
繼續新增50。這一步相對與B樹同樣存在一些特殊步驟，更新內部的索引結點，插入50之前，31是最大值，索引結點存儲11,31表明 目前31對應子樹關鍵字范圍在(11,31]之間，但是插入50之后，沿路的索引值也需要進行更新

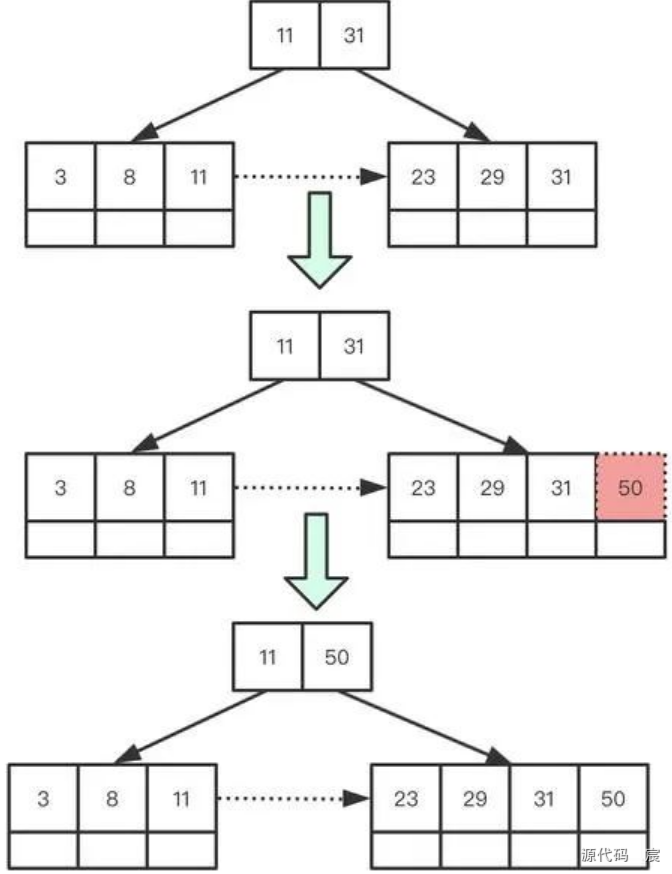
最后插入28，1，2，這次插入無需更新沿路的索引結點，因為其并未打破索引的范圍規則

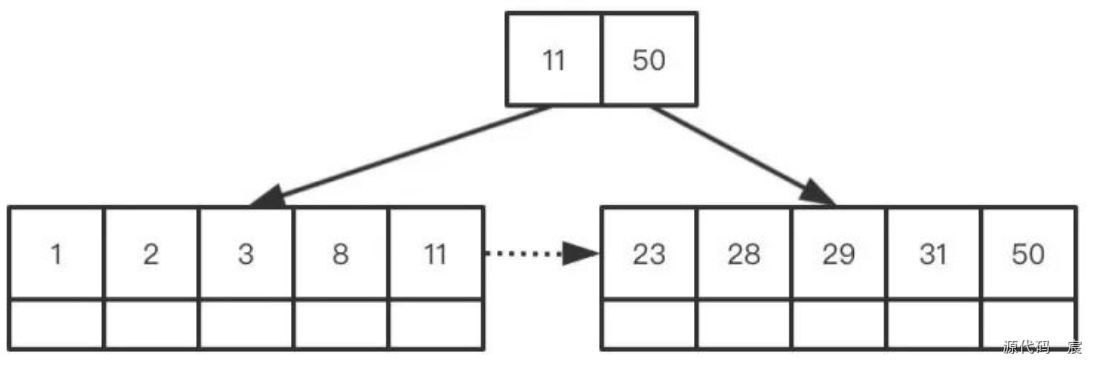
通過新增的流程，我們會發現，相比較B樹，插入邏輯要復雜一些。復雜在當插入結點打破索引規則時， 需要更新沿路索引，其次對于分裂的葉子結點需要形成一個單向鏈表

刪除

新增操作之后繼續看刪除的流程，我們依次刪除50，23，28，1，2。

刪除50后，雖然結點多于最小關鍵字個數，但是索引結點的平衡被打破，即不存在50的索引，所以需要更新索引結點。

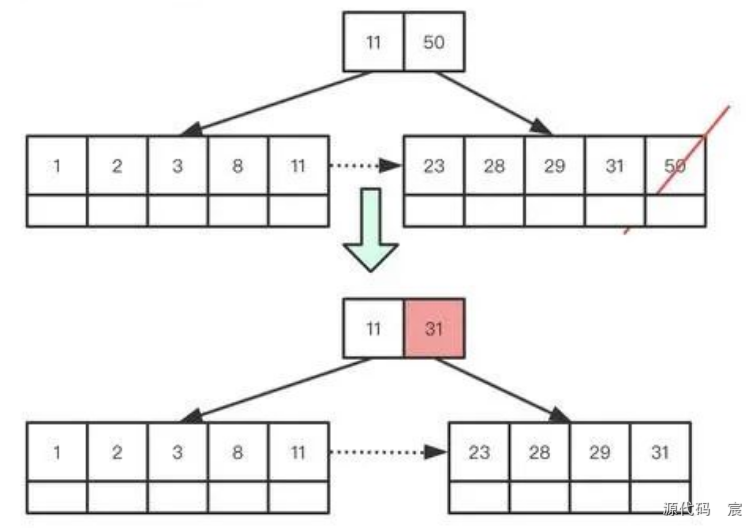
刪除23的過程中，即沒有打破索引，也沒有導致結點關鍵字少于最小關鍵字個數，所以整棵樹并沒有大的改動， 但是當我們刪除28的時候，結點最關鍵字小于最小關鍵字個數。此時就需要借結點或者合并結點。針對刪除28，我們會發現，他的左兄弟結點關鍵字個數大于最小關鍵字個數，所以可以借用，借用過程：借用左兄弟最大關鍵字或者右兄弟最小關鍵字，如果是借用左兄弟，則更新左兄弟對應父結點的索引值(因為最大關鍵字被借走)， 如果借用右兄弟則更新當前結點對應父結點的索引值(因為借過來的肯定比當前索引值大)

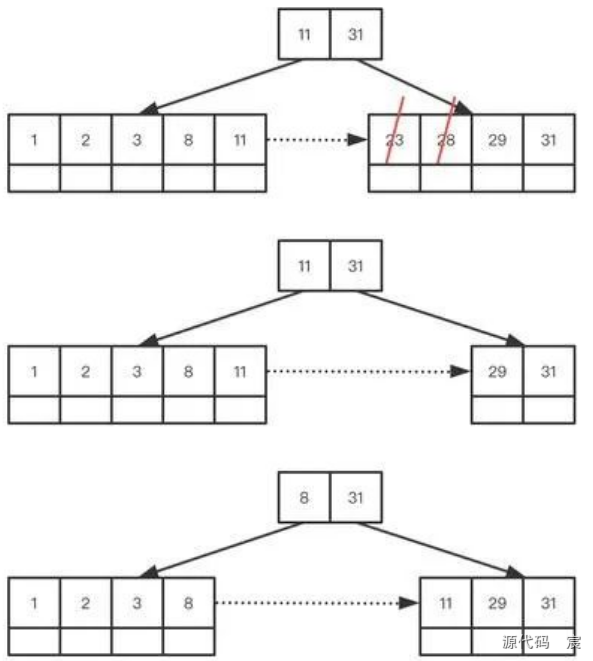
繼續刪除1，2。在刪除2的過程中，結點關鍵字個數少于最小關鍵字個數，此時兄弟結點的關鍵字個數無法外借(因為已經是最少關鍵字)， 此時進行合并，合并流程：如果合并之后根結點孩子不足2，則移除根結點，合并結點充當根結點，如果合并之后，根結點孩子大于等于2， 則將被合并結點對應父結點的索引值移除。

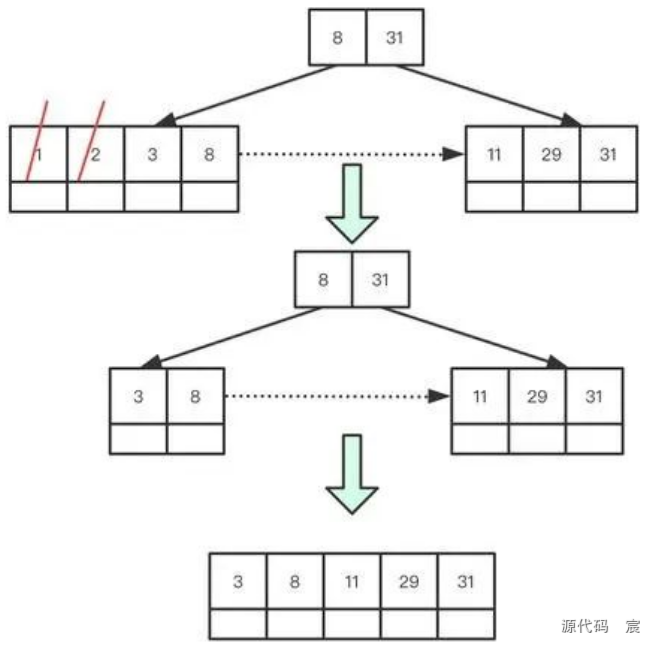
六、感受B+樹的威力

前面說到，B樹/B+樹與紅黑樹等二叉樹相比，最大的優勢在于樹高更小。實際上，對于Innodb的B+索引來說，樹的高度一般在2-4層。下面來進行一些具體的估算。

樹的高度是由階數決定的，階數越大樹越矮；而階數的大小又取決于每個節點可以存儲多少條記錄。Innodb中每個節點使用一個頁(page)，頁的大小為16KB，其中元數據只占大約128字節左右(包括文件管理頭信息、頁面頭信息等等)，大多數空間都用來存儲數據。

B+ 樹和 B 樹的區別？

為什么 B+ 樹比 B 樹更適合應用于數據庫索引？

七、總結

之后我會持續更新，如果喜歡我的文章，請記得一鍵三連哦，點贊關注收藏，你的每一個贊每一份關注每一次收藏都將是我前進路上的無限動力 ！！！↖(▔▽▔)↗感謝支持！