在支持向量機的分類模型中，我們會遇到兩大類模型，一類是線性可分的模型，還有一類是非線性可分的。非線性可分模型是基于線性可分的基礎上來處理的。支持向量機比較適合小樣本的訓練。

線性可分

如下圖所示，有紫色和黑色兩類，可以用一條直線對數據進行完全分類。這樣叫做線性可分

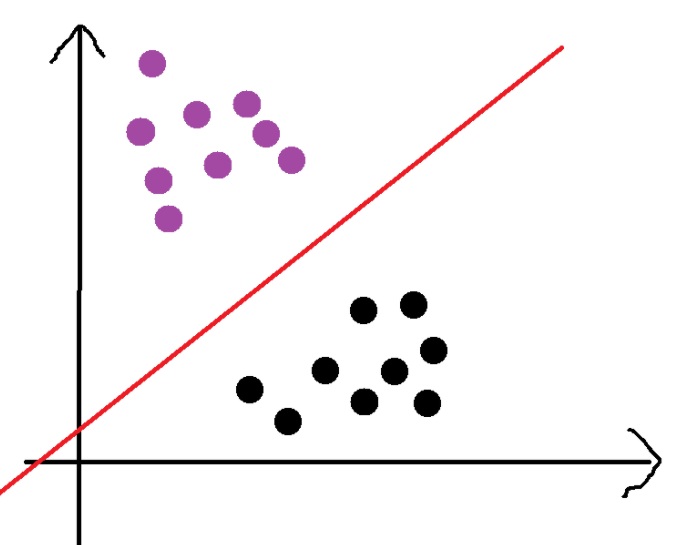
由上圖我們可以看出，這兩類點可以由無限根直線給分割開，那么我們該怎么找出最好的那一根呢？我們該怎么衡量最好的呢？我們該怎么用數學表達式來表述出這個最好的那個數學表達式呢？

具體做法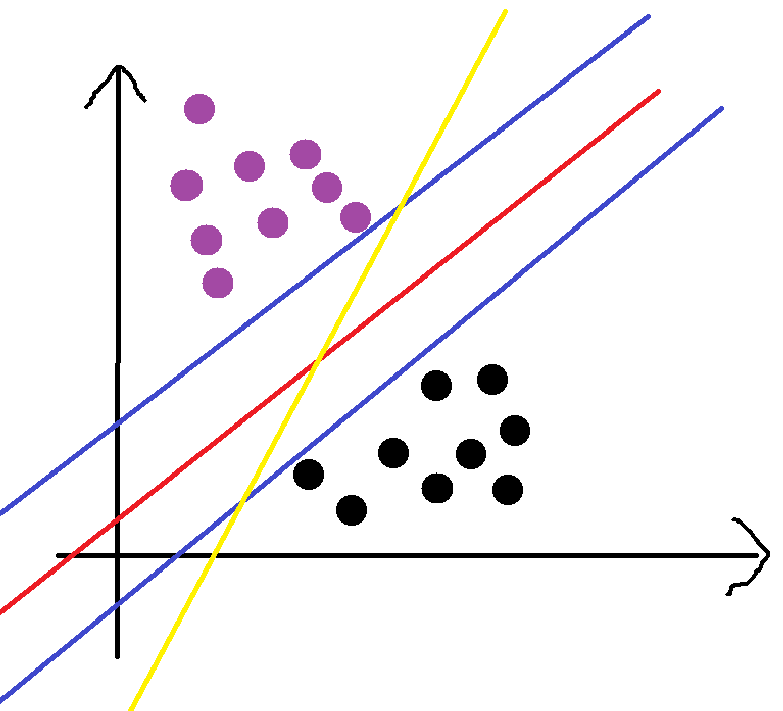

光憑感覺，我們可以知道，上圖中的紅線最好，可能從兩方面想到，紅線的數據的權重相對于黃線考慮到的更多，更重要的是紅線對數據誤差的容忍度更高，因為紅線剛好處于中間數據萬一由于錯誤偏移一點，也是可以分類正確的。我們該怎么量化這個呢？

找最優

上圖中，兩條藍線是經過紅線平移，平移到恰好與黑點或者紫點相交的位置。要求最好，所以我們要讓這兩條線之間的距離d最大，這樣也就確定了斜率值，但是在這兩條藍線中存在無數條紅線，我們要確定紅線我們還要讓d/2最大，這樣也就確定了截距。這樣我們就語言描述出最好是什么樣的了，下面我們來用數學公式表達出。（藍線剛好要碰到的點就是支持向量）

定義

在我們進行數學公式表達之前，我們先對需要的進行定義。

1 訓練數據及標簽

????????????????????????????????????????

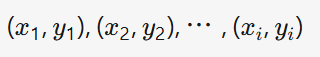
這里我們假設數據為二維的（其實一樣的，二維的我們建立的是一條線，如果是三維的，我們就建立一個最優平面，如果是高維的我們就建立一個最優的超平面，所用公式一樣。）

這里標簽我們就假設為????????+1??和? -1（方面后面計算，對結果沒影響）

2 訓練模型

??????????????????????????????????????????????????????????????????????

這里是W和X是相同維度的

3 線性可分

必要知識

1?

后面雖然乘a，但對這個線或者超平面是不會發生改變的。

2 點到線距離公式（向量到超平面距離公式）

特征縮放

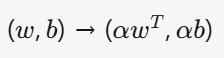?????????????????????????????????????????????????????（a>0）

我們進行這一操作，對超平面的幾何位置不會產生任何改變。

根據這個我們可以寫出，肯定會存在一個a使得

??????????????????????????????????????????????????????????????????????????????????

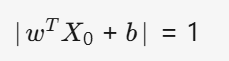
這里等于1只是為了方便計算，意思就是使得支持向量?X0??到超平面的函數間隔等于 1。

縮放后，支持向量滿足?∣w?X0?+b∣=1，此時所有其他樣本點滿足?∣w?Xi?+b∣≥1

這樣上面d的公式就變為了??????????????????????????????????????

????????????????????????????????????????????????????????????????????

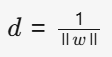
我們要求d的最大值，也就是求分母W的最小值。

優化問題

????????????????????????最小化?????? ? ??????????????????????

????????????????????????限制條件? ? ? ? ? ? ??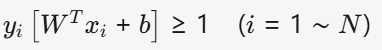

線性不可分

這類又存在兩種情況，一種是???????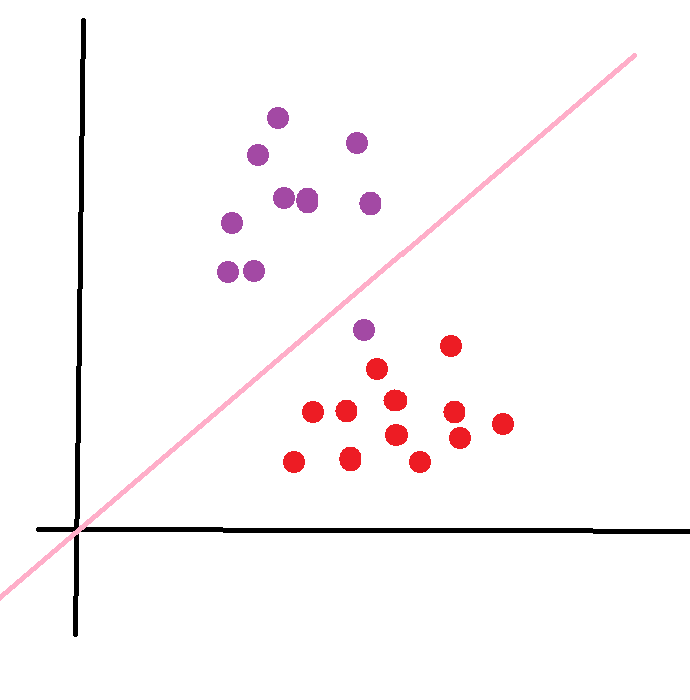

上面這類情況，和我們上面差不多，我們可以用直線給分隔開，但是代價太高了，所有我們可以加上一個松弛變量

目標函數（最小化）????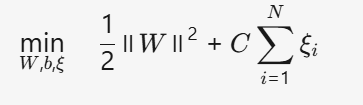

高維映射

上面對非線性的處理還是不夠的，因為有可能會存在下面一種情況。

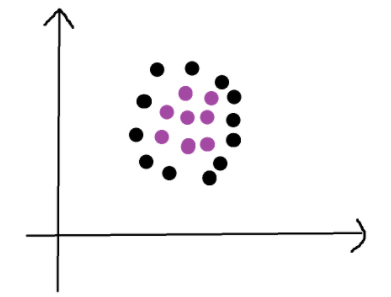
對于上面，我們不可能用一條線給分開了，這個時候我們要把低維向量映射到高維中，這樣就可分了。在一個平面上取若干點，不同類，如果我們維度函數轉化為無限維，這樣我們可以分類所有的分類的問題。下面我舉一個特別簡單的小例子

簡單示例

???????????????????????????????????????????????????????????????????????????????????

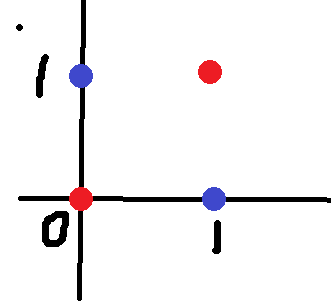
在這樣一個數據中，不存在一條線能完全把紅藍兩類點分開。

其中???????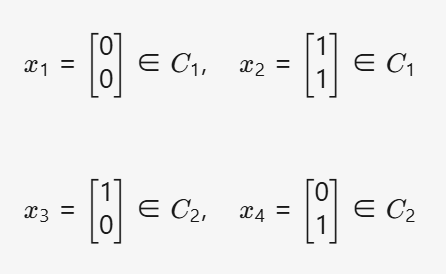

我們想著是不是可以把這個映射到高維中，然后就可以用一個超平面來分隔，這個映射的法則就叫做核函數。

核函數

核函數（Kernel Function）是支持向量機（SVM）中的關鍵組件，用于將原始輸入數據映射到高維特征空間，從而解決非線性分類問題。核函數通過隱式計算高維空間的內積，避免了顯式映射的計算復雜度。

我們假設一個法則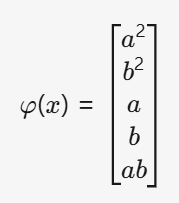

轉化為：???????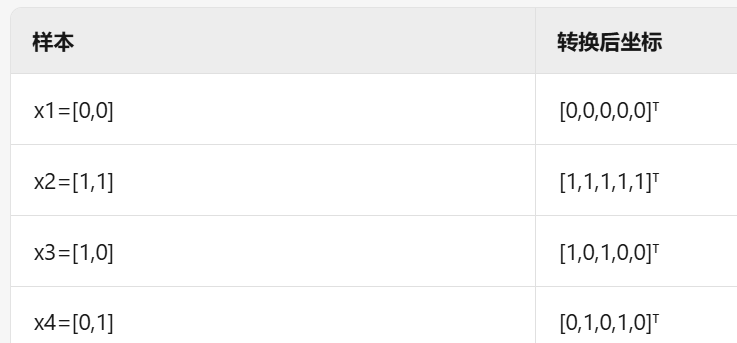

于是我們可以構造一個超平面??????????????

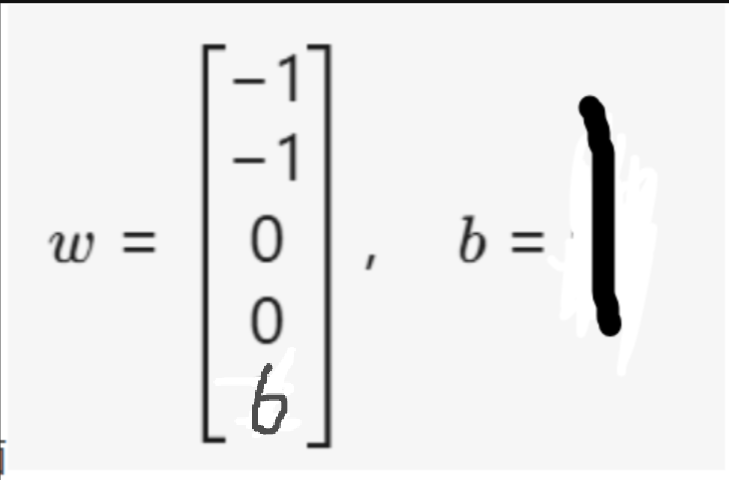
可以把他們分割

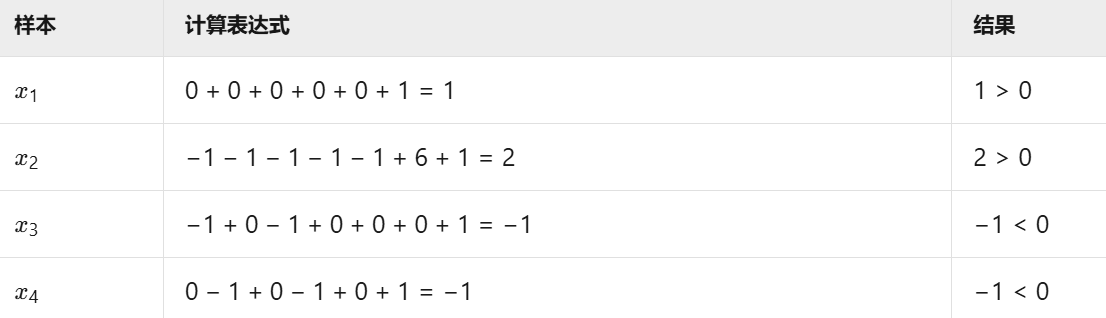
高維映射的優化式子

求最優W和b

SVM中的API接口

SVC( C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, 
cache_size=200, class_weight=None, verbose=False, max_iter=- 1, decision_function_shape='ovr', 
break_ties=False, random_state=None)

上面全是默認參數值

以下是 SVC（支持向量分類器）中最關鍵的參數及其簡明解析，基于專業實踐和文檔總結

：

代碼實戰

import pandas as pd
data=pd.read_csv('iris.csv')
print(data.head())
X=data.iloc[:,[1,3]]
y=data.iloc[:,5]
from sklearn.model_selection import train_test_split
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)from sklearn.svm import SVC
model = SVC(kernel='linear', C=float('inf'))
# model = SVC(kernel='linear', C=1)
model.fit(X, y)
# y_pred = model.predict(X_test)a=model.coef_[0]
b=model.intercept_[0]print(a,b)from sklearn import metrics
print(metrics.classification_report(y,model.predict(X)))import matplotlib.pyplot as plt
import numpy as npX1=data[data.iloc[:,5]==1].iloc[:,[1,3]]
X0=data[data.iloc[:,5]==0].iloc[:,[1,3]]plt.scatter(X1.iloc[:,0],X1.iloc[:,1],c='red')
plt.scatter(X0.iloc[:,0],X0.iloc[:,1],c='blue')x1=np.linspace(0,7,100)
x2=(x1*a[0]-b)/a[1]         #-b!!!并且這里
x3=(x1*a[0]-b+1)/a[1]
x4=(x1*a[0]-b-1)/a[1]
plt.plot(x1,x2)
plt.plot(x1,x3)
plt.plot(x1,x4)
plt.show()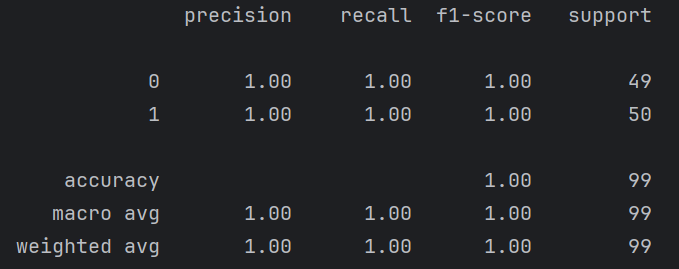

下面是對其中兩個特征進行劃分的結果圖。可以看出準確率特別高。

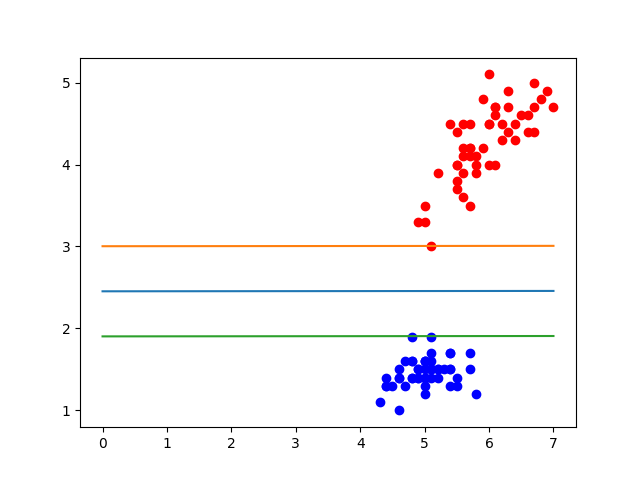
總結

1 float('inf')表示無限大

2 繪圖的時候注意是WX+b=0,要把一個x作為縱坐標要稍加處理

3 這個如果訓練的時候對數據做切分處理了，可能有未被計算的點離我們的超平面距離小于1。