目錄
用 SVM 實現鳶尾花數據集分類:從代碼到可視化全解析
一、算法原理簡述
二、完整代碼實現
三、代碼解析
1. 導入所需庫
2. 加載并處理數據
3. 劃分訓練集和測試集
4. 訓練 SVM 模型
5. 計算決策邊界參數
6. 生成決策邊界數據
7. 繪制樣本點
8. 繪制決策邊界
9. 設置坐標軸范圍
10. 標記支持向量
11. 顯示圖像
用 SVM 實現鳶尾花數據集分類:從代碼到可視化全解析
支持向量機(SVM)是一種經典的機器學習算法,特別適合處理小樣本、高維空間的分類問題。本文將通過鳶尾花(Iris)數據集,從零開始實現基于 SVM 的分類任務,并通過可視化直觀展示分類效果。
一、算法原理簡述
SVM 的核心思想是尋找最大間隔超平面,通過這個超平面將不同類別的數據分開。對于線性可分的數據,存在無數個可分超平面,SVM 會選擇距離兩類數據最近點(支持向量)距離最大的那個超平面,從而獲得更好的泛化能力。
當數據線性不可分時,SVM 可以通過核函數將低維數據映射到高維空間,使其在高維空間中線性可分。本文使用線性核(kernel='linear')進行演示,適合處理線性可分的鳶尾花數據集。
二、完整代碼實現
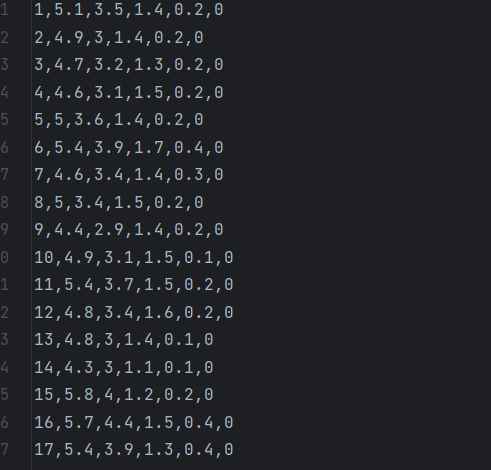
下面是基于鳶尾花數據集的 SVM 分類完整代碼,包含數據加載、模型訓練、決策邊界可視化等功能:部分數據集如下:
import pandas as pd
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import metrics# 1. 加載數據
f = pd.read_csv('iris.csv') # 讀取鳶尾花數據集# 2. 數據劃分(按類別拆分用于可視化)
data = f.iloc[:50,:] # 第一類數據(前50條)
data1 = f.iloc[50:,:] # 后兩類數據(第50條之后)# 3. 準備特征和標簽
x = f.iloc[:,[1,3]] # 選擇第2列和第4列作為特征(萼片寬度和花瓣寬度)
y = f.iloc[:,-1] # 最后一列為標簽(花的類別)# 4. 劃分訓練集和測試集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0) # 20%數據作為測試集# 5. 初始化并訓練SVM模型
svm = SVC(kernel='linear', C=1, random_state=0) # 線性核,正則化參數C=1
svm.fit(x_train, y_train)# 6. 獲取模型參數(用于繪制決策邊界)
w = svm.coef_[0] # 權重系數
b = svm.intercept_[0] # 偏置項# 7. 生成決策邊界數據
x1 = np.linspace(0,7,300) # 生成300個從0到7的均勻點
x2 = -(w[0]*x1 + b)/w[1] # 決策邊界公式:w0*x1 + w1*x2 + b = 0 → 求解x2
x3 = 1 + x2 # 邊界1(決策邊界+1)
x4 = -1 + x2 # 邊界2(決策邊界-1)# 8. 繪制散點圖(樣本點)
plt.scatter(data.iloc[:,1], data.iloc[:,3], marker='+', color='b', label='第一類')
plt.scatter(data1.iloc[:,1], data1.iloc[:,3], marker='*', color="r", label='其他類別')# 9. 繪制決策邊界
plt.plot(x1, x3, linewidth=1, color='r', linestyle='--', label='邊界1')
plt.plot(x1, x2, linewidth=2, color='r', label='決策邊界')
plt.plot(x1, x4, linewidth=1, color='r', linestyle='--', label='邊界2')# 10. 設置坐標軸范圍
plt.xlim(4,7)
plt.ylim(0,5)# 11. 標記支持向量
vets = svm.support_vectors_ # 獲取支持向量
plt.scatter(vets[:,0], vets[:,1], c='b', marker='x', label='支持向量')# 12. 添加圖例和標題
plt.legend()
plt.title('SVM分類鳶尾花數據集(線性核)')
plt.show()# 13. 模型評估
y_pred = svm.predict(x_test)
print("模型準確率:", metrics.accuracy_score(y_test, y_pred))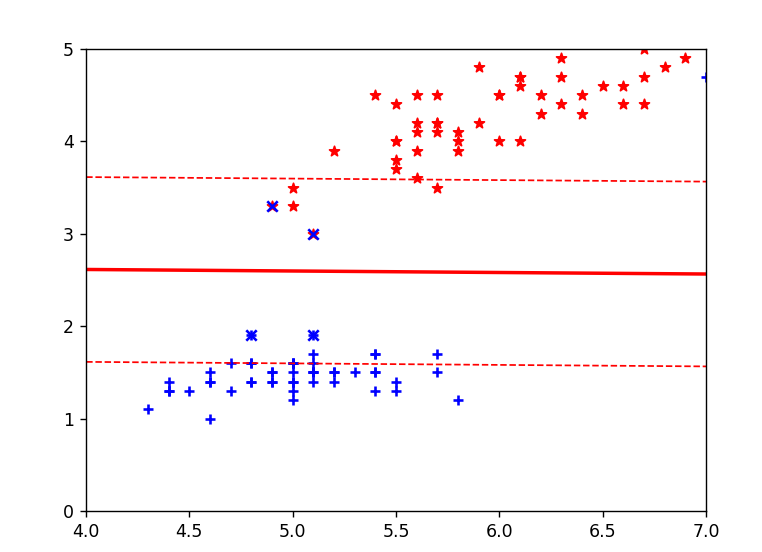
三、代碼解析
1. 導入所需庫
import pandas as pd # 用于數據處理和分析
from sklearn.svm import SVC # 從sklearn庫導入支持向量分類器
import numpy as np # 用于數值計算
import matplotlib.pyplot as plt # 用于數據可視化
from sklearn.model_selection import train_test_split # 用于劃分訓練集和測試集
from sklearn import metrics # 用于模型評估2. 加載并處理數據
f = pd.read_csv('iris.csv') # 讀取鳶尾花數據集(CSV格式)鳶尾花數據集包含 100?條樣本,分為 2類鳶尾花,每條樣本有 4 個特征(花萼長度、花萼寬度、花瓣長度、花瓣寬度)和 1 個標簽(花的類別)。
data = f.iloc[:50,:] # 取前50條數據(第一類鳶尾花,通常是setosa)
data1 = f.iloc[50:,:] # 取第50條之后的數據(后兩類鳶尾花,通常是versicolor和virginica)這里按行索引拆分數據,用于后續可視化時區分不同類別。
x = f.iloc[:,[1,3]] # 選擇特征:取所有行的第2列(索引1)和第4列(索引3)
y = f.iloc[:,-1] # 選擇標簽:取所有行的最后一列(花的類別)- 特征選擇第 2 列和第 4 列(通常對應花萼寬度和花瓣寬度),便于二維可視化
- 標簽為最后一列(花的種類)
3. 劃分訓練集和測試集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0) # 劃分數據集x_train:訓練集特征(80% 的數據)x_test:測試集特征(20% 的數據)y_train:訓練集標簽y_test:測試集標簽test_size=0.2:測試集占比 20%random_state=0:隨機種子,保證每次運行劃分結果一致
4. 訓練 SVM 模型
svm = SVC(kernel='linear', C=1, random_state=0) # 初始化SVM模型
svm.fit(x_train, y_train) # 用訓練集訓練模型kernel='linear':使用線性核函數(適用于線性可分數據)C=1:正則化參數,控制對誤分類的懲罰程度(值越大懲罰越重)random_state=0:隨機種子,保證結果可復現fit():訓練模型,通過訓練集學習特征與標簽的關系
5. 計算決策邊界參數
w = svm.coef_[0] # 獲取權重系數(對于線性核,shape為[特征數])
b = svm.intercept_[0] # 獲取偏置項(截距)對于線性 SVM,決策邊界是一個超平面,二維情況下是一條直線,公式為:
![]()
(其中(w0, w1)是權重,b是偏置,(x1, x2)是兩個特征)
6. 生成決策邊界數據
x1 = np.linspace(0,7,300) # 生成300個從0到7的均勻點(作為x軸數據)
x2 = -(w[0]*x1 + b)/w[1] # 計算決策邊界的y值(由超平面公式推導)
x3 = 1 + x2 # 決策邊界上方的輔助線(間隔邊界)
x4 = -1 + x2 # 決策邊界下方的輔助線(間隔邊界)x1是橫軸坐標,x2是決策邊界在對應x1處的縱軸坐標x3和x4是決策邊界兩側的間隔邊界,用于展示 SVM 的 "最大間隔" 特性
7. 繪制樣本點
# 繪制第一類樣本(藍色+號)
plt.scatter(data.iloc[:,1], data.iloc[:,3], marker='+', color='b')
# 繪制后兩類樣本(紅色*號)
plt.scatter(data1.iloc[:,1], data1.iloc[:,3], marker='*', color="r")scatter():繪制散點圖data.iloc[:,1]和data.iloc[:,3]:分別取第一類樣本的第 2 列和第 4 列特征作為 x、y 坐標marker:指定點的形狀(+ 號和 * 號區分不同類別)
8. 繪制決策邊界
plt.plot(x1, x3, linewidth=1, color='r', linestyle='--') # 上方間隔邊界(虛線)
plt.plot(x1, x2, linewidth=2, color='r') # 決策邊界(實線)
plt.plot(x1, x4, linewidth=1, color='r', linestyle='--') # 下方間隔邊界(虛線)plot():繪制直線- 紅色實線是 SVM 找到的最優決策邊界,虛線是間隔邊界,兩條虛線之間的距離是 "最大間隔"
9. 設置坐標軸范圍
plt.xlim(4,7) # x軸范圍設置為4到7
plt.ylim(0,5) # y軸范圍設置為0到5限制坐標軸范圍,使圖像聚焦在樣本密集區域,更清晰地展示分類效果。
10. 標記支持向量
vets = svm.support_vectors_ # 獲取支持向量(距離決策邊界最近的樣本點)
plt.scatter(vets[:,0], vets[:,1], c='b', marker='x') # 用x標記支持向量- 支持向量是決定決策邊界位置的關鍵樣本,SVM 的決策僅由這些點決定
vets[:,0]和vets[:,1]:支持向量的兩個特征值
11. 顯示圖像
plt.show() # 顯示繪制的圖像總結
這段代碼的核心邏輯是:
- 加載鳶尾花數據集并選擇特征
- 劃分訓練集和測試集
- 訓練線性 SVM 模型
- 計算并繪制決策邊界、間隔邊界
- 可視化樣本點和支持向量

 86. 分隔鏈表(鏈表+雙指針))
)


)
)
)








:AI+Apache ECharts:生成各種專業圖表)
下)

