C++ 模擬實現 map 和 set：掌握核心數據結構

---

---

一、set 和 map 的結構

STL中set和map底層是一顆紅黑樹，模擬set和map需要一顆紅黑樹作為我們的成員變量
點擊這里了解紅黑樹

---

1.1 set的結構

set結構就是 K模型，所以set容器對紅黑樹的封裝如下：

---

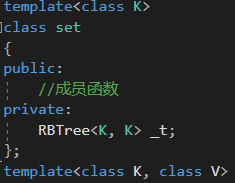
1.2 map的結構

map結構就是 KV模型，所以map容器對紅黑樹的封裝如下

---

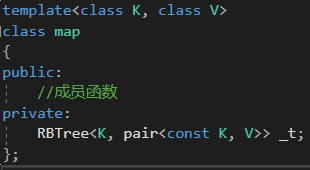
二、對紅黑樹的改造

---

2.1 改造紅黑樹的節點

其中紅黑樹的節點類型就是模版參數T

---

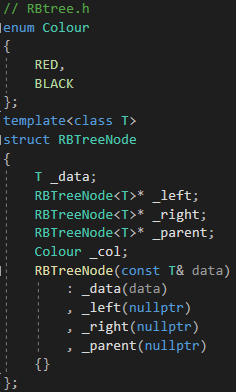
2.2 改造紅黑樹

2.2.1 仿函數的使用

---

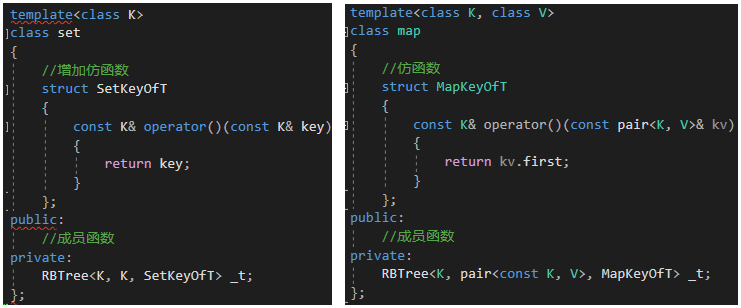
然后我們將所有需要比較key的函數利用仿函數進行替換，我們以Find為例

---

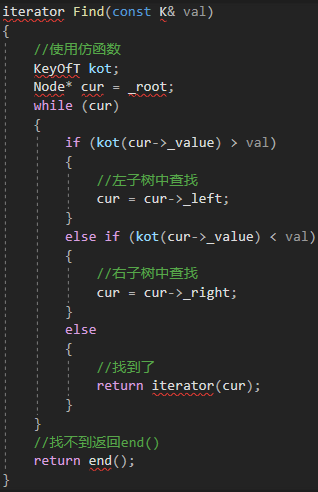
2.2.2 插入函數的改造

代碼如下（示例）：

pair<iterator, bool> Insert(const T& data)
{//情況一：如果是根節點if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(iterator(_root),true);}KeyOfT kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_value) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_value) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(iterator(cur), false);}}//找到插入位置cur = new Node(data);Node* newnode = cur;if (kot(parent->_value) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//情況三：如果叔叔存在且為紅if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{//情況四：叔叔不存在/存在且為黑，且cur在parent的左側if (cur == parent->_left){//     g  //   p   u// c RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//情況五：叔叔不存在 / 存在且為黑，cur在parent的右側{//     g//   p   u//     cRotateLR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//這時該子樹的根節點變為黑色，不需要繼續調整break;}}else{Node* uncle = grandfather->_left;//情況三：如果叔叔存在且為紅if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//繼續調整cur = grandfather;parent = cur->_parent;}else{//情況四：叔叔不存在/存在且為黑，且cur在parent的左側if (cur == parent->_right){//    g//  u   p//        cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else // 情況五：叔叔不存在 / 存在且為黑，cur在parent的右側{//    g//  u   p//    cRotateRL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//這時該子樹的根節點變為黑色，不需要繼續調整break;}}}//防止情況三改到根節點變為紅色_root->_col = BLACK;return make_pair(iterator(newnode), true);
}

---

2.2.3 刪除函數的改造

代碼如下（示例）：

else //待刪除結點的左右子樹均不為空
{//替換法刪除//尋找待刪除結點右子樹當中key值最小的結點作為實際刪除結點Node* minParent = cur;Node* minRight = cur->_right;while (minRight->_left){minParent = minRight;minRight = minRight->_left;}// 原本直接可以賦值// cur->_value = minRight->_value //將待刪除結點的鍵值改為minRight的鍵值Node* newnode = new Node(minRight->_value,cur->_col);Node* parent = cur->_parent;//重新鏈接祖父孫三代節點關系cur->_left->_parent = newnode;cur->_right->_parent = newnode;if (parent){if (parent->_left == cur){parent->_left = newnode;}else{parent->_right = newnode;}}else{//如果是根節點_root = newnode;}newnode->_parent = parent;newnode->_left = cur->_left;newnode->_right = cur->_right;//如果minParent是curif (minParent == cur){minParent = newnode;}delete cur;delParent = minParent; //標記實際刪除的父節點delCur = minRight; //標記實際刪除的結點
}

---

三、對迭代器的改造

3.1 *、->、！=、==

代碼如下（示例）：

template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{typedef RBNode<T> Node;typedef __RBTreeIterator<T, Ref, Ptr> Self;Node* _node;//構造__RBTreeIterator(Node* node):_node(node){}Ref operator*(){return _node->_value;}Ptr operator->(){return &_node->_value;}//判斷兩個正向迭代器是否不同bool operator!=(const Self& s) const{return _node != s._node;}//判斷兩個正向迭代器是否相同bool operator==(const Self& s) const{return _node == s._node;}Node* getNode(){return _node;}
};

---

3.2 begin和end

代碼如下（示例）：

typedef __RBTreeIterator<T, T&, T*> iterator;//普通迭代器
typedef __RBTreeIterator<T, const T&, const T*> const_iterator;//const迭代器
//最左節點
iterator begin()
{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);
}
iterator end()
{return iterator(nullptr);
}
//const版本begin和end
const_iterator begin()const
{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);
}const_iterator end()const
{return const_iterator(nullptr);
}

---

3.3 ++ 和 –

代碼如下（示例）：

 //前置++Self& operator++(){//如果右子樹不為空if (_node->_right){//尋找該結點右子樹當中的最左結點Node* left = _node->_right;while (left->_left){left = left->_left;}_node = left;}else{Node* cur = _node;Node* parent = cur->_parent;//尋找孩子不在右的祖先while (parent && cur == parent->_right){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}//前置--Self& operator--(){if (_node->_left) //結點的左子樹不為空{//尋找該結點左子樹當中的最右結點Node* right = _node->_left;while (right->_right){right = right->_right;}_node = right;}else{//尋找孩子不在父親左的祖先Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}

---

3.4 const迭代器

代碼如下（示例）：

//普通迭代器構造const迭代器
__RBTreeIterator(const __RBTreeIterator<T,T&,T*>& it):_node(it._node)
{}

---

3.5 復用紅黑樹接口實現set/map中的成員函數

3.5.1 set成員函數

代碼如下（示例）：

template<class K>
class set
{struct SetKeyOfT{const K& operator()(const K& key){return key;}};
public://typename聲明是一個類型而不是靜態變量typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;//成員函數iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}pair<iterator, bool> insert(const K& key){return _t.Insert(key);}//刪除函數void erase(const K& key){_t.Erase(key);}//查找函數iterator find(const K& key){return _t.Find(key);}
private:RBTree<K, K, SetKeyOfT> _t;
};

---

3.5.2 map成員函數

代碼如下（示例）：

template<class K, class V>
class map
{//仿函數struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};
public://typename聲明是一個類型而不是靜態變量typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator; typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;//成員函數iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}pair<iterator, bool> insert(const pair<K,V>& key){return _t.Insert(key);}//刪除函數void erase(const K& key){_t.Erase(key);}//查找函數iterator find(const K& key){return _t.Find(key);}//[]運算符重載V& operator[](const K& key){pair<iterator, bool> ret = _t.Insert(make_pair(key, V()));return ret.first->second;}
private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};

---

---

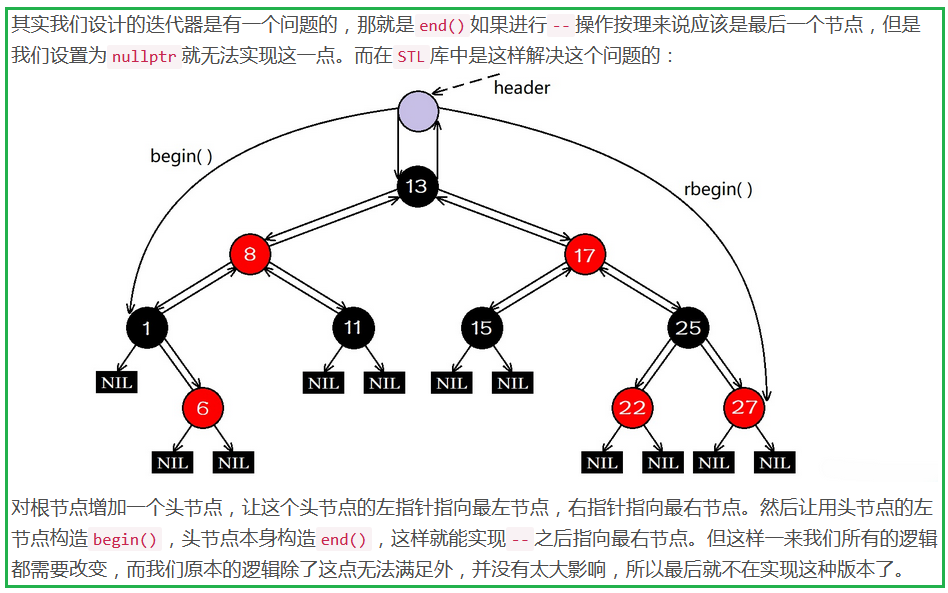
四、源代碼總結

4.1 Myset.h

代碼如下（示例）：

#pragma once
// Myset.h
#include"RBTree.h"
namespace bit
{template<class K>class set{struct SetKeyOfT{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, const K, SetKeyOfT>::Iterator iterator;typedef typename RBTree<K, const K, SetKeyOfT>::ConstIteratorconst_iterator;iterator begin(){return _t.Begin();}iterator end(){return _t.End();}const_iterator begin() const{return _t.Begin();}const_iterator end() const{return _t.End();}pair<iterator, bool> insert(const K& key){return _t.Insert(key);}iterator find(const K& key){return _t.Find(key);}private:RBTree<K, const K, SetKeyOfT> _t;};void Print(const set<int>& s){set<int>::const_iterator it = s.end();while (it != s.begin()){--it;// 不?持修改//*it += 2;cout << *it << " ";}cout << endl;}void test_set(){set<int> s;int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){s.insert(e);}for (auto e : s){cout << e << " ";}cout << endl;Print(s);}
}

---

4.2 Mymap.h

代碼如下（示例）：

#pragma once
#include"RBTree.h"
namespace bit
{template<class K, class V>class map{struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iteratoriterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIteratorconst_iterator;iterator begin(){return _t.Begin();}iterator end(){return _t.End();}const_iterator begin() const{return _t.Begin();}const_iterator end() const{return _t.End();}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}iterator find(const K& key){return _t.Find(key);}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};void test_map(){map<string, string> dict;dict.insert({ "sort", "排序" });dict.insert({ "left", "左邊" });dict.insert({ "right", "右邊" });dict["left"] = "左邊，剩余";dict["insert"] = "插?";dict["string"];map<string, string>::iterator it = dict.begin();while (it != dict.end()){// 不能修改first，可以修改second//it->first += 'x';it->second += 'x';cout << it->first << ":" << it->second << endl;++it;}cout << endl;}
}

---

4.3 RBTree.h

代碼如下（示例）：

#pragma once
#include<iostream>
using namespace std;// RBtree.h
enum Colour
{RED,BLACK
};
template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;RBTreeNode(const T& data): _data(data), _left(nullptr), _right(nullptr), _parent(nullptr){}
};
template<class T, class Ref, class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ref, Ptr> Self;Node* _node;Node* _root;RBTreeIterator(Node* node, Node* root):_node(node), _root(root){}Self& operator++(){if (_node->_right){// 右不為空，右?樹最左結點就是中序第?個Node* leftMost = _node->_right;while (leftMost->_left){leftMost = leftMost->_left;}_node = leftMost;}else{// 孩?是?親左的那個祖先Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}Self& operator--(){if (_node == nullptr) // end(){// --end()，特殊處理，?到中序最后?個結點，整棵樹的最右結點Node* rightMost = _root;while (rightMost && rightMost->_right){rightMost = rightMost->_right;}_node = rightMost;}else if (_node->_left){// 左?樹不為空，中序左?樹最后?個Node* rightMost = _node->_left;while (rightMost->_right){rightMost = rightMost->_right;}_node = rightMost;}else{// 孩?是?親右的那個祖先Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = cur->_parent;}_node = parent;}return *this;}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!= (const Self& s) const{return _node != s._node;}bool operator== (const Self& s) const{return _node == s._node;}
};
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef RBTreeIterator<T, T&, T*> Iterator;typedef RBTreeIterator<T, const T&, const T*> ConstIterator;Iterator Begin(){Node* leftMost = _root;while (leftMost && leftMost->_left){leftMost = leftMost->_left;}return Iterator(leftMost, _root);}Iterator End(){return Iterator(nullptr, _root);}ConstIterator Begin() const{Node* leftMost = _root;while (leftMost && leftMost->_left){leftMost = leftMost->_left;}return ConstIterator(leftMost, _root);}ConstIterator End() const{return ConstIterator(nullptr, _root);}RBTree() = default;~RBTree(){Destroy(_root);_root = nullptr;}pair<Iterator, bool> Insert(const T & data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(Iterator(_root, _root), true);}KeyOfT kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(Iterator(cur, _root), false);}}cur = new Node(data);Node* newnode = cur;// 新增結點。顏?紅?給紅?cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;// g// p uif (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// u存在且為紅 -》變?再繼續往上處理parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{// u存在且為?或不存在 -》旋轉+變?if (cur == parent->_left){// g// p u//c//單旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// c//雙旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{// g// u pNode* uncle = grandfather->_left;// 叔叔存在且為紅，-》變?即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上處理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在，或者存在且為?{// 情況?：叔叔不存在或者存在且為?// 旋轉+變?// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(Iterator(newnode, _root), true);
}
Iterator Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return Iterator(cur, _root);}}return End();
}
private:void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parentParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parentParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}
private:Node* _root = nullptr;
};

---