?

目錄

1.計數排序的思想

2.計數排序圖解?

?3.計數排序代碼邏輯

3.1求原數組最大最小值及計數數組的創建

3.2計數

3.3覆蓋寫

3.4釋放資源

4.計數排序的注意事項

5.計數排序的時間復雜度與空間復雜度

---

以升序為例

1.計數排序的思想

前面我們學習的快排、歸并排序、希爾排序........等等都是需要比較大小才能使數組有序的方法，而計數排序屬于非比較排序

計數排序的核心思想在于，借助計數數組來統計原數組中各個元素的出現次數，隨后通過覆蓋寫等一系列操作，最終達成將原數組排序為有序序列的目的

2.計數排序圖解?

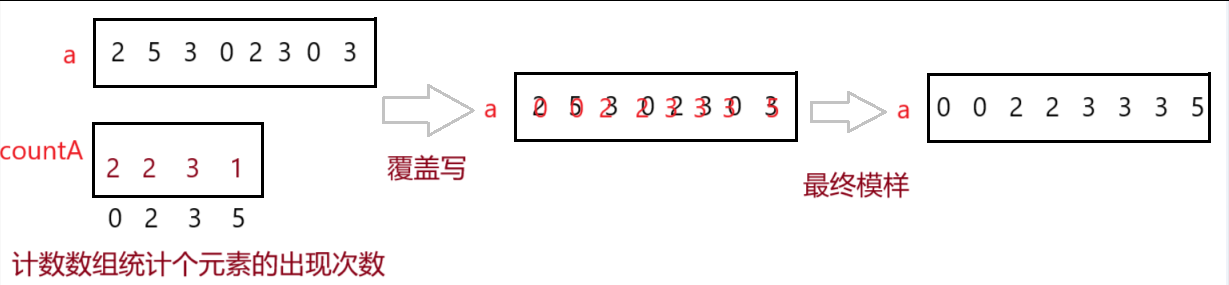
?3.計數排序代碼邏輯

3.1求原數組最大最小值及計數數組的創建

//求最大最小值
int max = a[0], min = a[0];
for (int i = 1; i < n; ++i){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];
}//開計數數組
int range = max - min + 1;
int* countA = (int*)calloc(range, sizeof(int));
if (!countA){perror("malloc fail");return;
}

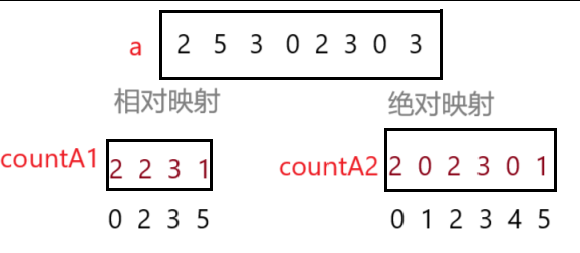
這是一種相對位置映射的思想，簡單來說

原數組的最小元素代表計數數組的第一個位置，以此類推，最大值代表計數數組的最后一個位置

相對映射比絕對映射節省空間

絕對映射需要開至少(萬一有負數)最大值個元素空間，當最大值是一萬，但最小值是9999時，空間浪費極大，所以實踐中多使用相對位置映射

所以計數數組 countA 的大小通常為 max - min + 1 ，元素初始值均為0

3.2計數

	for (int i = 0; i < n; ++i){countA[a[i] - min]++;}

min 代表的是計數數組的第一個位置，a[i] - min 計算的就是 a[i] 與 min 之間的差值，

這個差值正好對應 a[i] 代表的計數數組位置

3.3覆蓋寫

遍歷計數數組，根據原數組各元素的出現次數進行覆蓋寫

int j = 0;
for (int i = 0; i < range; ++i){while (countA[i]--){a[j++] = i + min;}
}

for循環是遍歷計數數組，while循環的循環次數是原數組各元素的出現次數

計數數組的下標 i 是 原數組各元素與min 的差值，即 i = a[ j ] - min

3.4釋放資源

free(countA);
countA = NULL;

防止內存泄漏哦~

4.計數排序的注意事項

計數排序只能排序整型

根據上述思想，計數排序更適合 范圍集中 的 整型數組

5.計數排序的時間復雜度與空間復雜度

計數排序的時間復雜度 基于 原數組和計數數組的 遍歷操作，

所以時間復雜度為 O(N + range)，當range接近N是，計數排序的效率極高！

計數排序的空間復雜度基于計數數組的創建

所以空間復雜度為O(range)

當然，如果有輸出數組的創建，空間復雜度為 O(N + range)