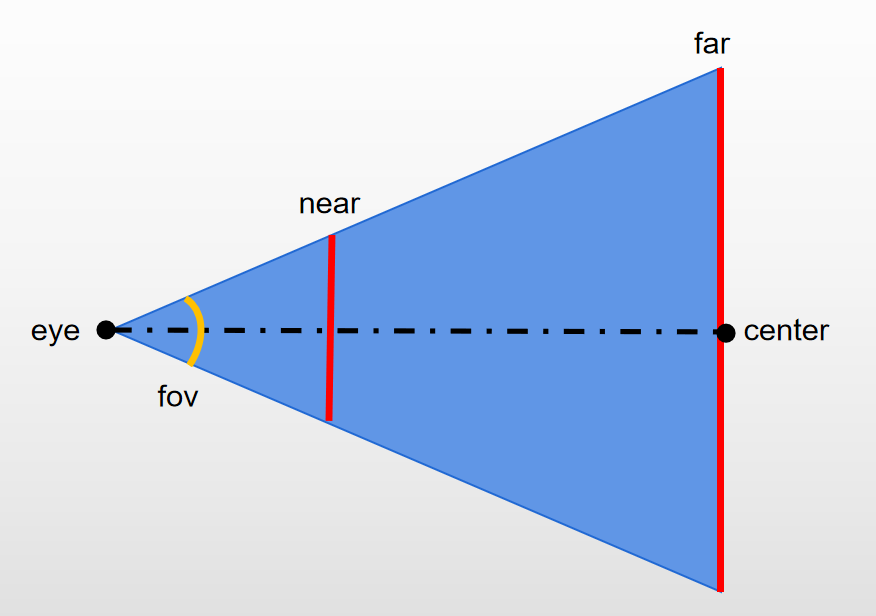
相機的核心構造一個是glm::lookAt函數,一個是glm::perspective函數,本文相機的一切運動都在于如何構建相應的參數傳入上述兩個函數里。
glm::mat4 glm::lookAt(glm::vec3 const &eye,//相機所在位置glm::vec3 const ¢er,//要凝視的點glm::vec3 const &up //相機上向量
);
glm::mat4 perspective(
float fovy,
float aspect,
float near,
float far);
首先我們通常默認相機的Front向量為(0,0,-1),位置eye為(0,0,0),則center=eye+Front=(0,0,-1)。
默認up向量為(0,1,0),通過Front向量和up向量可以叉積出right向量。
1.視角抬起與左右環視
通過修改Front向量即可。簡單點可直接用歐拉角,相機引入yaw跟pitch,麻煩點就直接用向量做。可知相機自身的Front向量,right向量以及叉積出來的Up向量(注意不是up向量),這三組向量構成一組坐標基。
//上下抬動thetaFront=Front*cos(theta)+Up*sin(theta)center=eye+Front;//up 不變,eye不變//上下旋轉動betaFront=Front*cos(beta)+right*sin(beta)center=eye+Front;//up 不變,eye不變2.視角平移
前后平移即通過Front向量平移,左右平移即通過right向量平移。將eye跟center加減Front向量和right向量即可實現平移。
//前后方向平移eye+=Front*k;//k為平移系數center+=Front*k;//up 不變//左右方向平移eye+=right*k;//k為平移系數center+=right*k;//up 不變3.zoomIn/zoomOut
1)普通的視野變換
直接通過修改fov即可,fov越大則視野越寬看到的東西更多,但是屏幕上呈現的物體會變小;反之則視野越窄看到的東西更少,但是屏幕上呈現的物體會變大
2)在鼠標位置進行區域的視野放大縮小
這時候直接修改fov就不管用了,需要通過平移相機的方式來實現。
獲取鼠標所在點映射的世界空間點P,然后讓相機沿著有eye與P兩點構成的向量前后移動即可達到zoomIn/zoomOut的效果。其本質還是利用了相似的性質,這種實現方法可以巧妙地保證鼠標所在位置對應的三維空間點永遠會在鼠標所對應的屏幕像素點上。
glm::vec3 dir=P-eye;//k為視野縮放系數,正數時zoomIn視野變大,負數則相反eye+=dir*k;center+=dir*k;//up 不變4.聚焦到某個物體
首先獲取到這個物體的包圍盒中心點P,然后用相機當前的Front向量與之加減獲得到新的相機的eye。然后將相機的center設置為P即可。
//k為系數,可以根據包圍盒的大小設置,包圍盒越大可以讓相機離遠點 eye=k*(P-Front);center=P;//up 不變5.繞某個物體旋轉
可以先聚焦到這個物體。接下來獲取到這個物體的包圍盒中心點P,這個P可固定為相機center,然后P與eye的距離為r。然后如果向上旋轉theta,相機的eye會繞著以P為球心,r為半徑的面沿著相機當前Up向量方向旋轉theta。如果向右旋轉,相機的eye會繞著以P為球心,r為半徑的面沿著相機當前right向量方向旋轉beta。當然,如果相機引入yaw跟pitch的話會相對更簡單一些。
// 計算單位球面上點P繞切線n旋轉theta角后的新坐標
// O: 球心
// P: 球面上的點
// n: 切線方向向量(需單位化且與OP垂直)
// theta: 旋轉角度(弧度)
glm::vec3 rotatePointOnSphere(const glm::vec3& O, const glm::vec3& P, const glm::vec3& n, float theta
)
{// 驗證輸入條件glm::vec3 OP = P - O;float opLength = glm::length(OP);// 檢查是否為單位球面(允許微小誤差)if (std::abs(opLength - 1.0f) > 1e-6f) {std::cerr << "警告:輸入點不在單位球面上,將進行歸一化處理" << std::endl;}// 檢查切線是否與半徑垂直float dotProduct = glm::dot(OP, n);if (std::abs(dotProduct) > 1e-6f) {std::cerr << "警告:輸入的切線方向不與半徑垂直,將重新計算垂直分量" << std::endl;}// 確保OP是單位向量glm::vec3 unitOP = glm::normalize(OP);// 確保n是單位向量且與OP垂直glm::vec3 tangent = glm::normalize(n - dotProduct * unitOP);// 創建旋轉四元數:繞切線方向旋轉theta角glm::quat rotation = glm::angleAxis(theta, tangent);// 執行旋轉:首先將點平移到原點,旋轉后再平移回球心glm::vec3 P_origin = P - O; // 點P相對于球心的坐標glm::vec3 P_rotated_origin = rotation * P_origin; // 旋轉glm::vec3 P_rotated = P_rotated_origin + O; // 平移回球心// 由于浮點誤差,可能需要重新歸一化以確保在單位球面上return O + glm::normalize(P_rotated - O);
}//繞P點上下轉動theta
center=P;
eye=rotatePointOnSphere(P,eye,Up,theta);
//up向量不變//繞P點左右轉動beta
center=P;
eye=rotatePointOnSphere(P,eye,right,beta);
//up向量不變












clamAV工具離線查殺)




)

