stack 和 queue

一、stack

1.1 stack 的介紹

1.2 stack的使用

1）最小棧

2）棧的彈出壓入序列

3）逆波蘭表達式求值

1.3 stack 的模擬使用

二、queue

2.1 queue的介紹

2.2 queue的使用

2.3 queue的模擬使用

三、容器適配器

3.1 什么是容器適配器

3.2 STL標準庫中stack 和 queue的底層結構

四、deque

4.1 deque的原理介紹

4.2 deque的缺陷

4.3 為什么選擇 deque 作為stack 和 queue的底層默認容器

五、priority_queue

5.1 priority_queue的介紹

5.2 priority_queue的使用

1）數組中第K個大的元素?

5.3 priority_queue的模擬實現?

一、stack

1.1 stack 的介紹

stack文檔 :?stack - C++ Reference

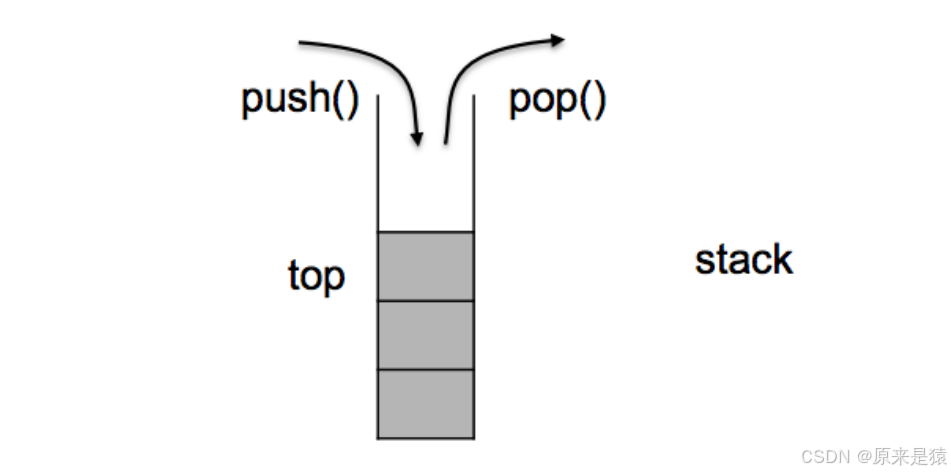
stack 不支持適配器 ，因為需要滿足 后進先出的 特性：

相關接口如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<stack>
using namespace std;int main()
{stack<int> st;st.push(1);st.push(2);st.push(3);st.push(4);while (!st.empty()){cout << st.top() << " ";st.pop();}cout << endl;return 0;
}

1.2 stack的使用

1）最小棧

155. 最小棧 - 力扣（LeetCode）

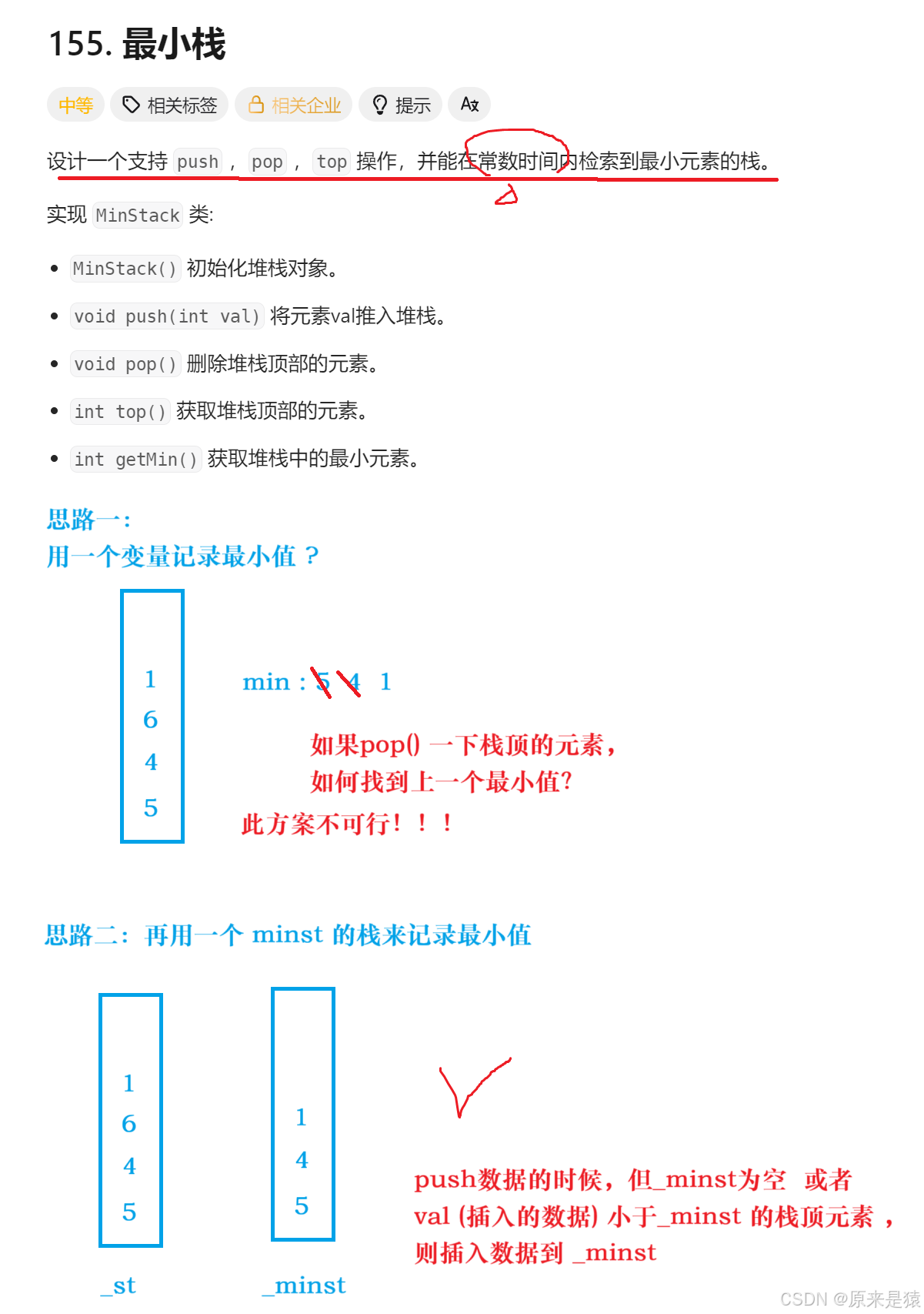
class MinStack {
public:void push(int val) {_st.push(val);if(_minst.empty() || val <= _minst.top())_minst.push(val);}void pop() {if(_st.top() == _minst.top())_minst.pop();_st.pop();}int top() {return _st.top();}int getMin() {return _minst.top();}stack<int> _st;stack<int> _minst;
};

2）棧的彈出壓入序列

棧的壓入、彈出序列_牛客題霸_牛客網

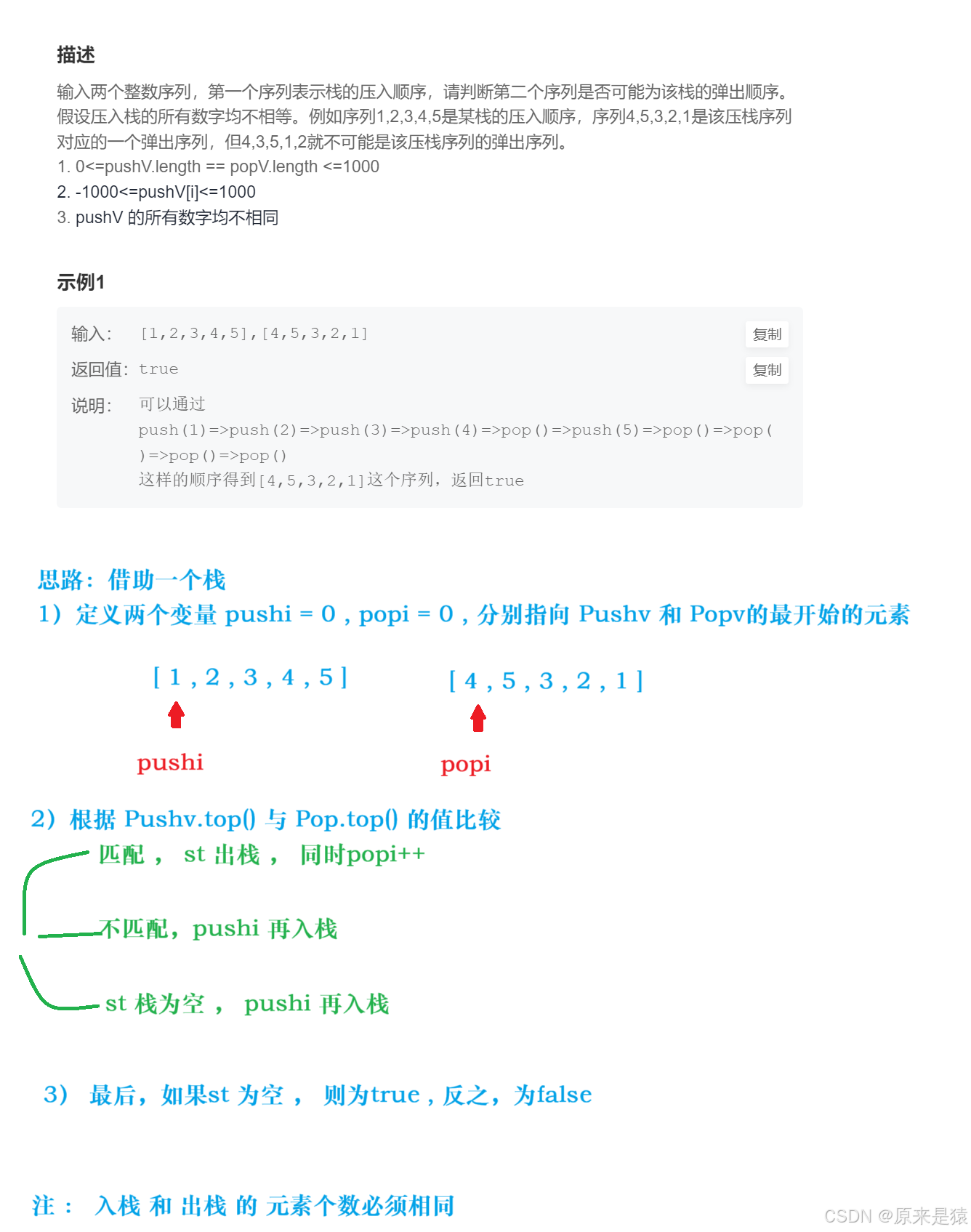
class Solution {
public:/*** 代碼中的類名、方法名、參數名已經指定，請勿修改，直接返回方法規定的值即可** * @param pushV int整型vector * @param popV int整型vector * @return bool布爾型*/bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {stack<int> st;size_t pushi = 0,popi = 0;while(pushi < pushV.size()){st.push(pushV[pushi++]);while(!st.empty() && st.top() == popV[popi]){st.pop();popi++;}}return st.empty();}
};

3）逆波蘭表達式求值

150. 逆波蘭表達式求值 - 力扣（LeetCode）

為了更加方便理解，下面是有關中綴表達式轉后綴表達式的題目，加深理解。

題號	中綴表達式	后綴表達式
1	`a + b - c`	`a b + c -`
2	`x * y / z`	`x y * z /`
3	`3 + 5 * 2`	`3 5 2 * +`
4	`10 - 6 / 3`	`10 6 3 / -`
5	`(a + b) * c`	`a b + c *`
6	`x / (y - z)`	`x y z - /`
7	`(3 + 5) * 2 - 4`	`3 5 + 2 * 4 -`
8	`10 - (2 * 3 + 5)`	`10 2 3 * 5 + -`
9	`a + (b * c - d) / e`	`a b c * d - e / +`
10	`( (3 + 5) * 2 ) / (10 - 8)`	`3 5 + 2 * 10 8 - /`
11	`x * (y + z) - w / v`	`x y z + * w v / -`
12	`(a - b) * (c + d / e)`	`a b - c d e / + *`

class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> st;for(auto & str:tokens){if(str == "+" || str == "-" || str == "*" || str == "/"){int right = st.top();st.pop();int left = st.top();st.pop();switch(str[0]){case '+':st.push(left + right);break;case '-':st.push(left - right);break;case '*':st.push(left * right);break;case '/':st.push(left / right);break;}}else{st.push(stoi(str));}}return st.top();}
};

1.3 stack 的模擬使用

通過復用來實現相關接口，?

stack.h

#pragma oncenamespace LF
{template<class T, class Container>class stack{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_back();}const T& top()const{return _con.back();}size_t size() const{return _con.size();}bool empty() const{return _con.empty();}private:Container _con;};
}

test.cpp 測試：

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<vector>
#include<list>
#include"Stack.h"
using namespace std;int main()
{//LF::stack<int,vector<int>> st;LF::stack<int,list<int>> st;st.push(1);st.push(2);st.push(3);st.push(4);while (!st.empty()){cout << st.top() << " ";st.pop();}cout << endl;return 0;
}

二、queue

queue文檔：queue - C++ Reference

2.1 queue的介紹

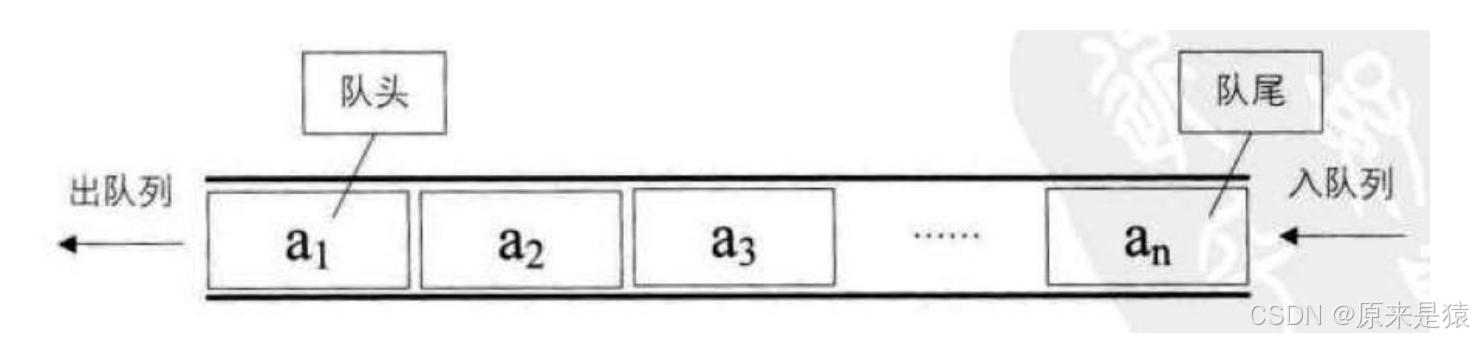
1. 隊列是一種容器適配器，專門用于在? FIFO上下文(先進先出)? 中操作，其中從容器一端插入元素，另一端提取元素 .

2.?隊列作為? 容器適配器? 實現，容器適配器即將特定容器類封裝作為其底層容器類，queue提供一組特定的成員函數來訪問其元素。元素從隊尾入隊列，從隊頭出隊列。

3. 底層容器可以是標準容器類模板之一，也可以是其他專門設計的容器類。該底層容器應至少支持以下操作：

empty：檢測隊列是否為空
size：返回隊列中有效元素的個數
front：返回隊頭元素的引用
back：返回隊尾元素的引用
push_back：在隊列尾部入隊列
pop_front：在隊列頭部出隊列

2.2 queue的使用

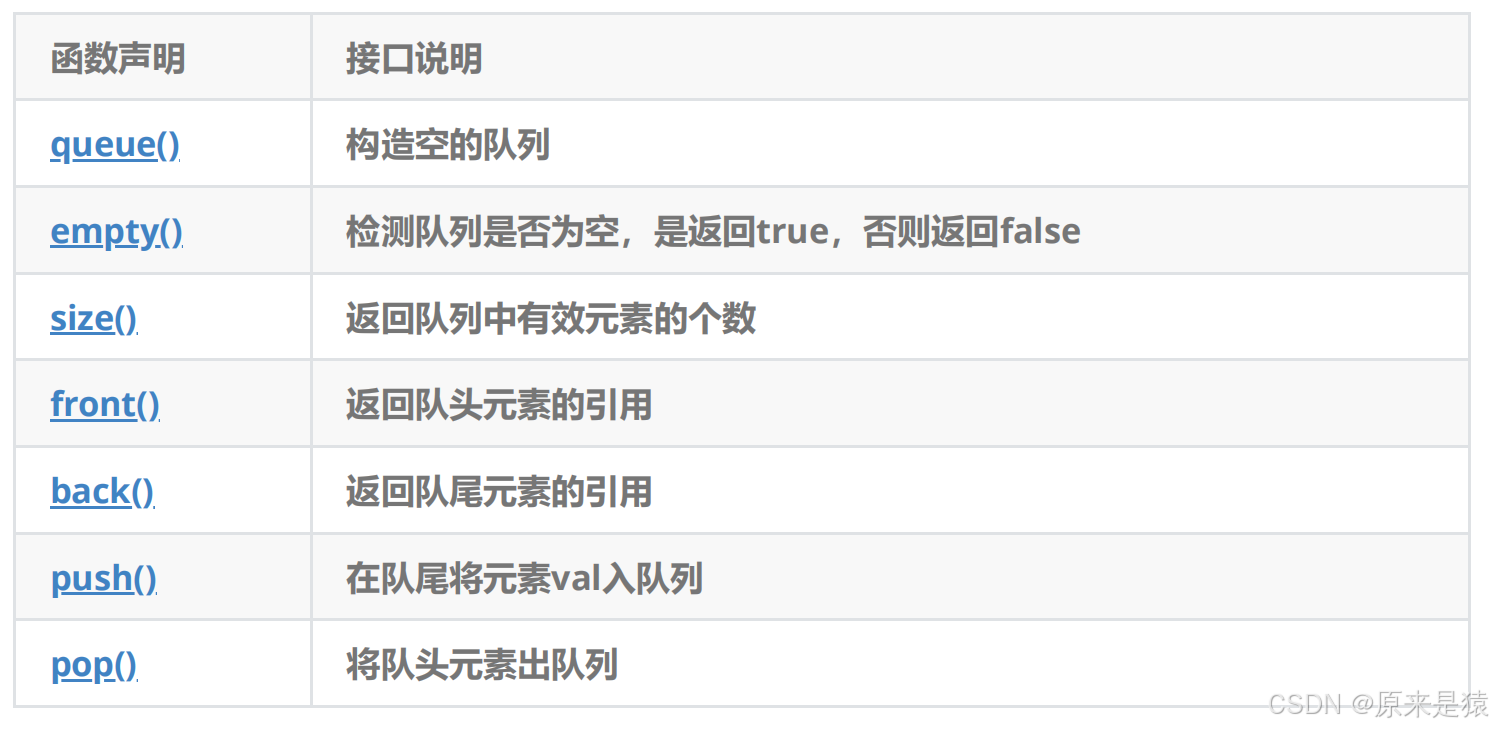
2.3 queue的模擬使用

注意 : vector 不能匹配隊列，因為 vector 不支持頭刪

queue.h

#pragma once
#include<deque>namespace LF
{template<class T, class Container = deque<T>>class queue{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_front();}const T& front() const{return _con.front();}const T& back() const{return _con.back();}size_t size() const{return _con.size();}bool empty() const{return _con.empty();}private:Container _con;};
}

test.cpp測試

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<stack>
#include<queue>
#include<vector>
#include<list>
#include"Stack.h"
using namespace std;
#include"queue.h"int main()
{LF::queue<int, list<int>> q;q.push(1);q.push(2);q.push(3);q.push(4);while (!q.empty()){cout << q.front() << " ";q.pop();}cout << endl;return 0;
}

三、容器適配器

3.1 什么是容器適配器

適配器是一種設計模式 （設計模式是一套被反復使用的、多人知曉的、經過反復編目的、代碼設計經驗的總結）， 該模式就是將一個類的接口轉換成客戶希望的另外一個接口。

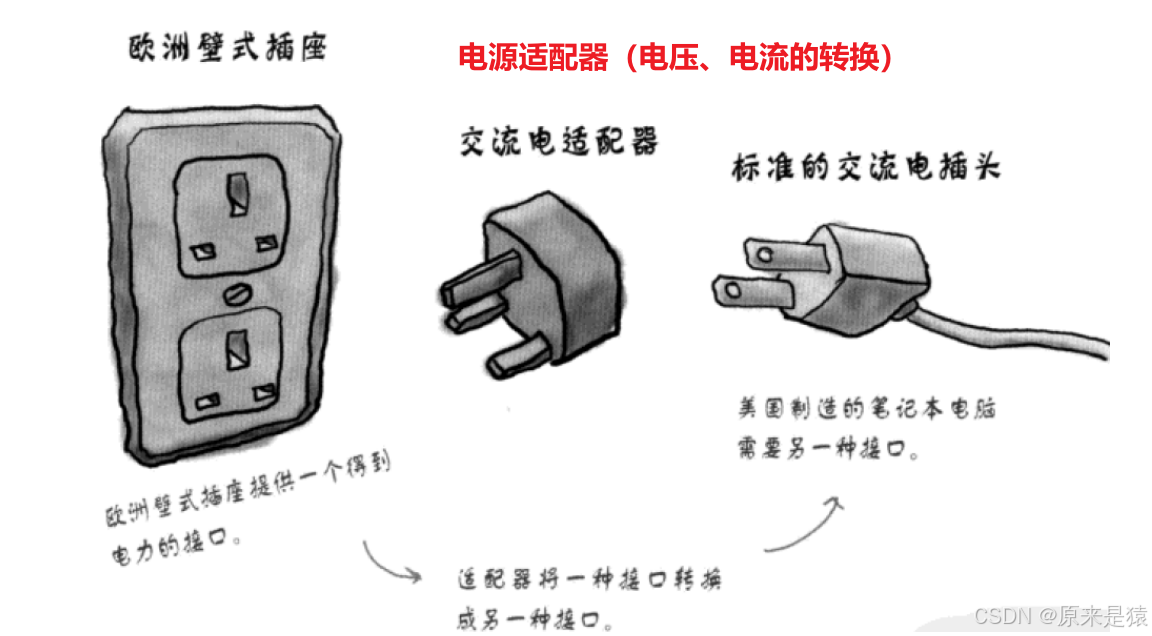
3.2 STL標準庫中stack 和 queue的底層結構

雖然 stack 和 queue中也可以存放元素，但在 STL中并沒有將其劃分在容器的行列 ，而是將其稱為容器適配器 ， 這是因為 stack 和隊列只是對其他容器的接口進行了包裝 ， STL中stack 和 queue 默認使用 deque , 如下：?

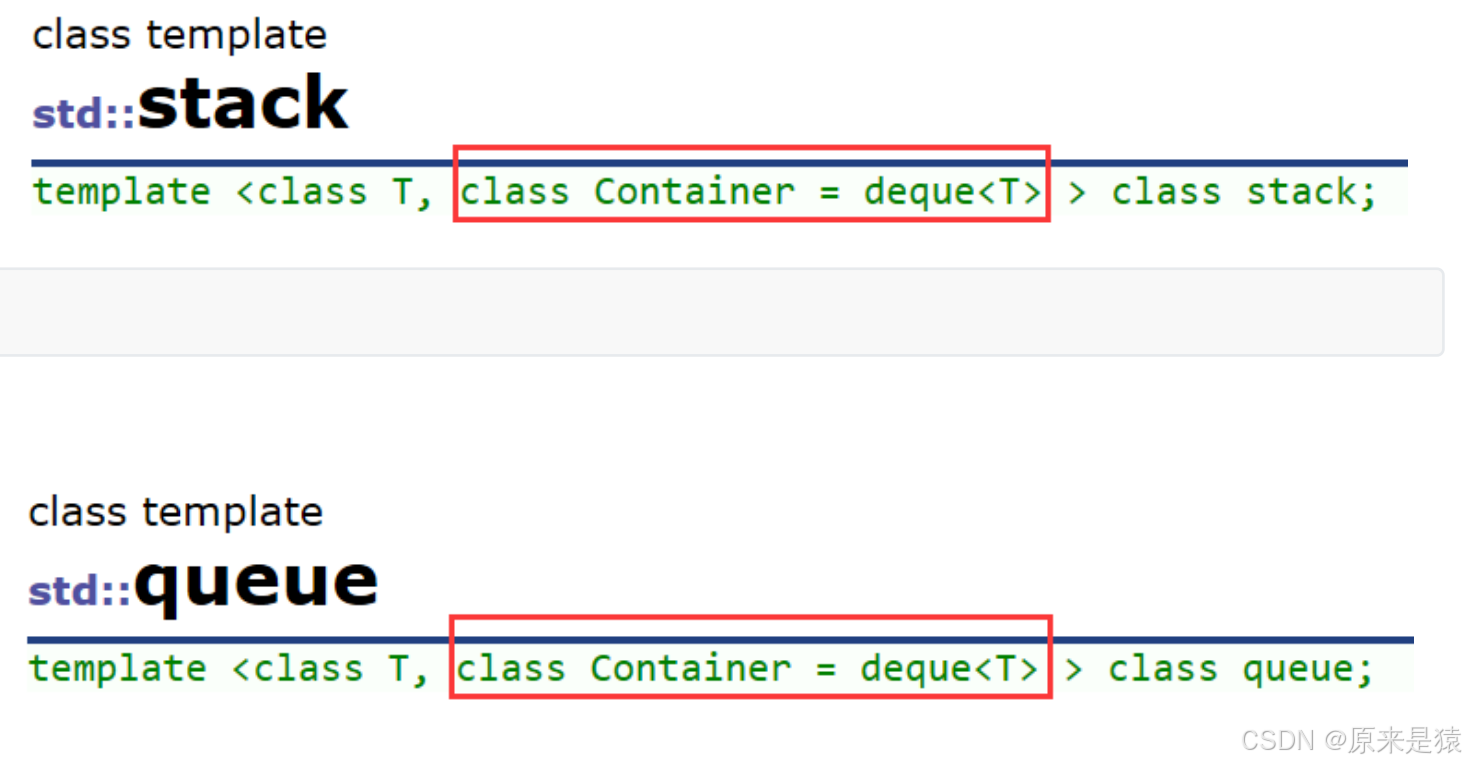
四、deque

4.1 deque的原理介紹

deque - C++ Reference

?deque(雙端隊列) ：是一種雙開口的“連續” 空間的數據結構， 雙開口的含義是：可以在頭尾兩端進行插入和刪除操作， 且時間復雜度為O(1) , 與 vector 比較，頭插效率高，不需要搬移元素；與list 比較，空間利用率高。

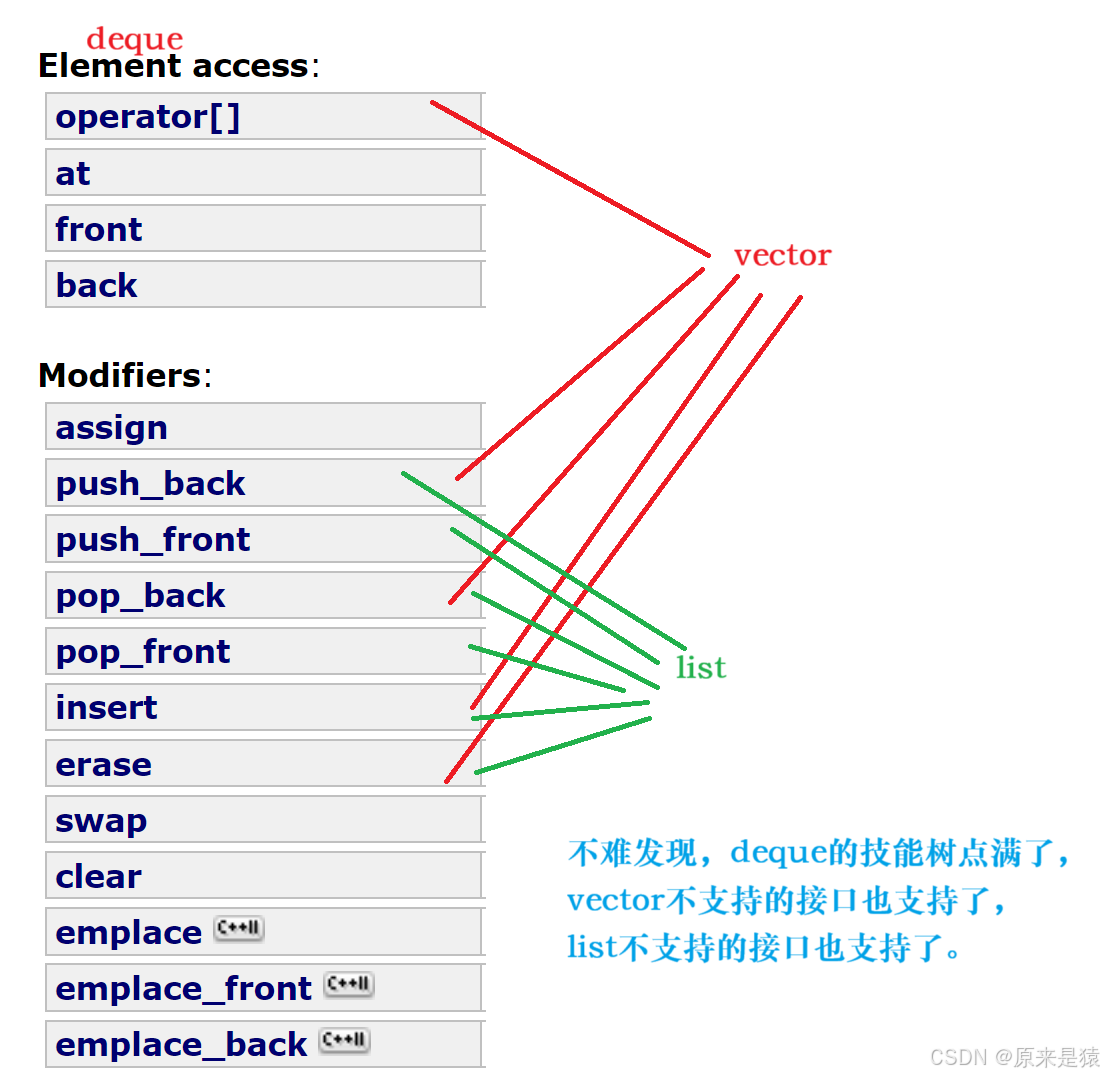
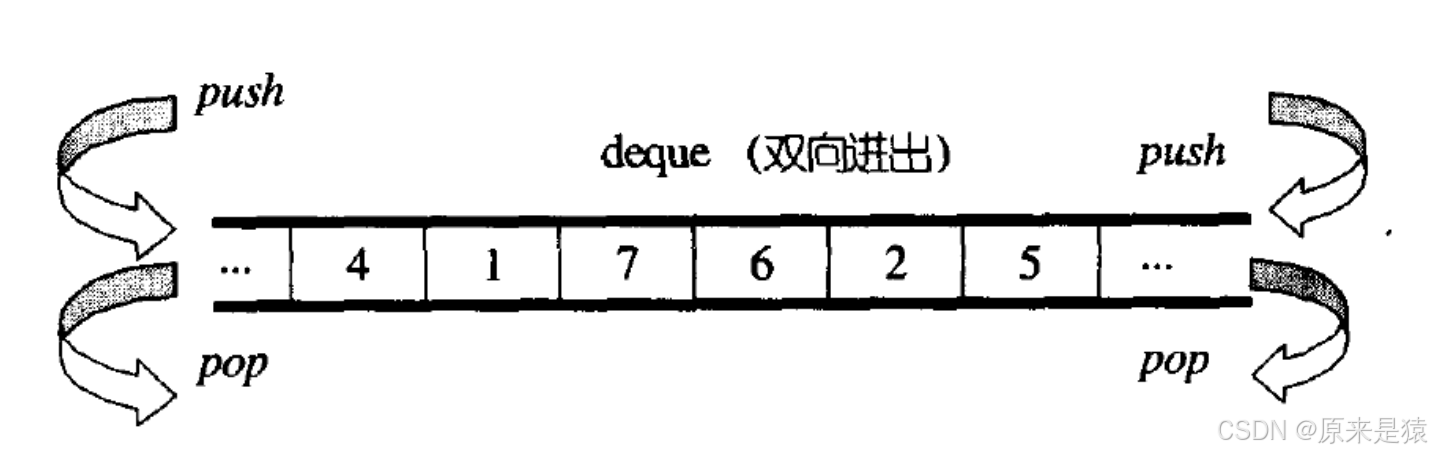
deque 并不是真正連續的空間，而是由一段段連續的小空間拼接而成的，實際deque類似于一個動態的二維數組，其底層結構如下圖所示：

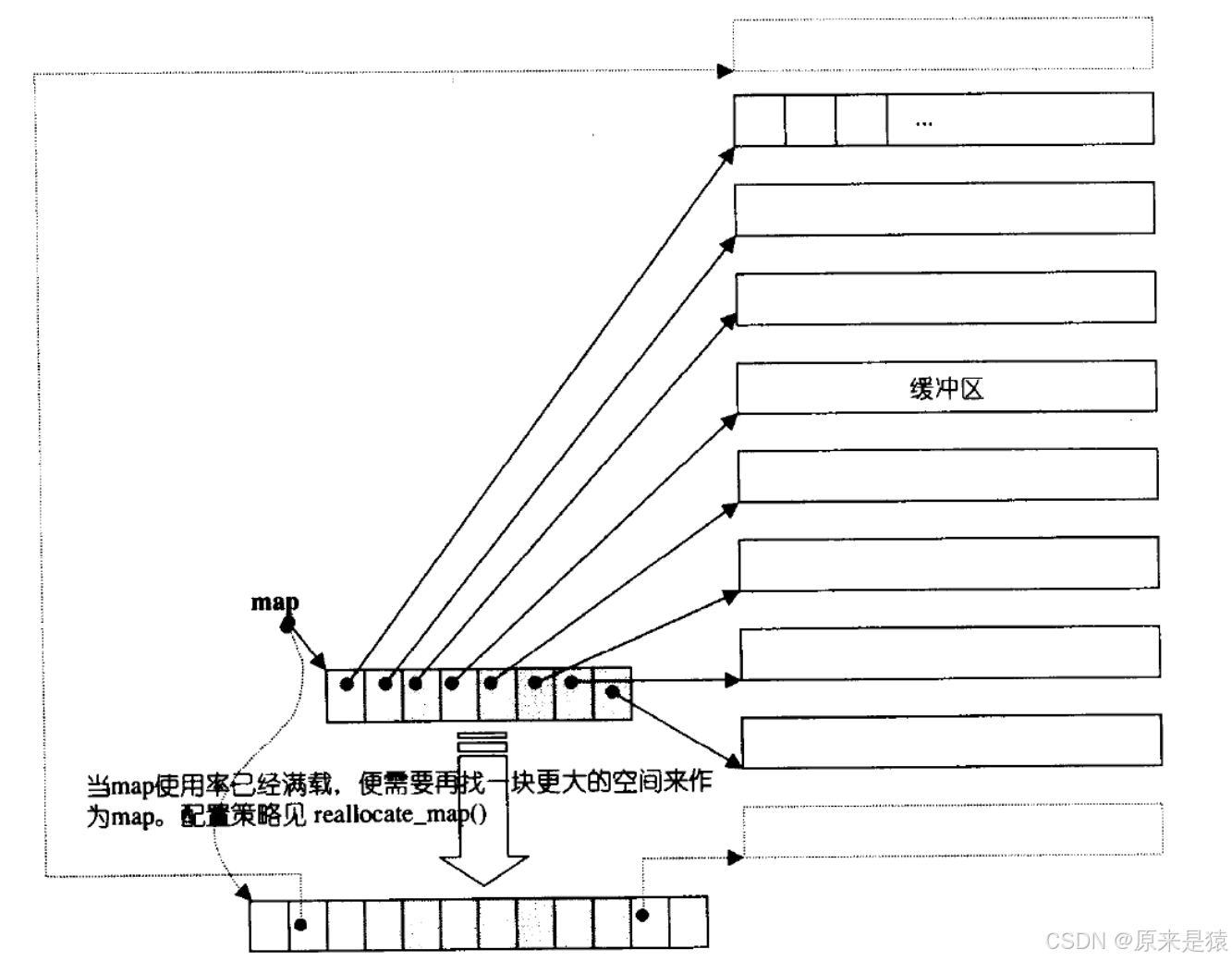
雙端隊列底層是一段假象的連續空間，實際是分段連續的，為了維護其 “整體連續” 以及隨機訪問的假象，落在了 deque的迭代器身上，因此 deque的迭代器設計就比較復雜，如下：

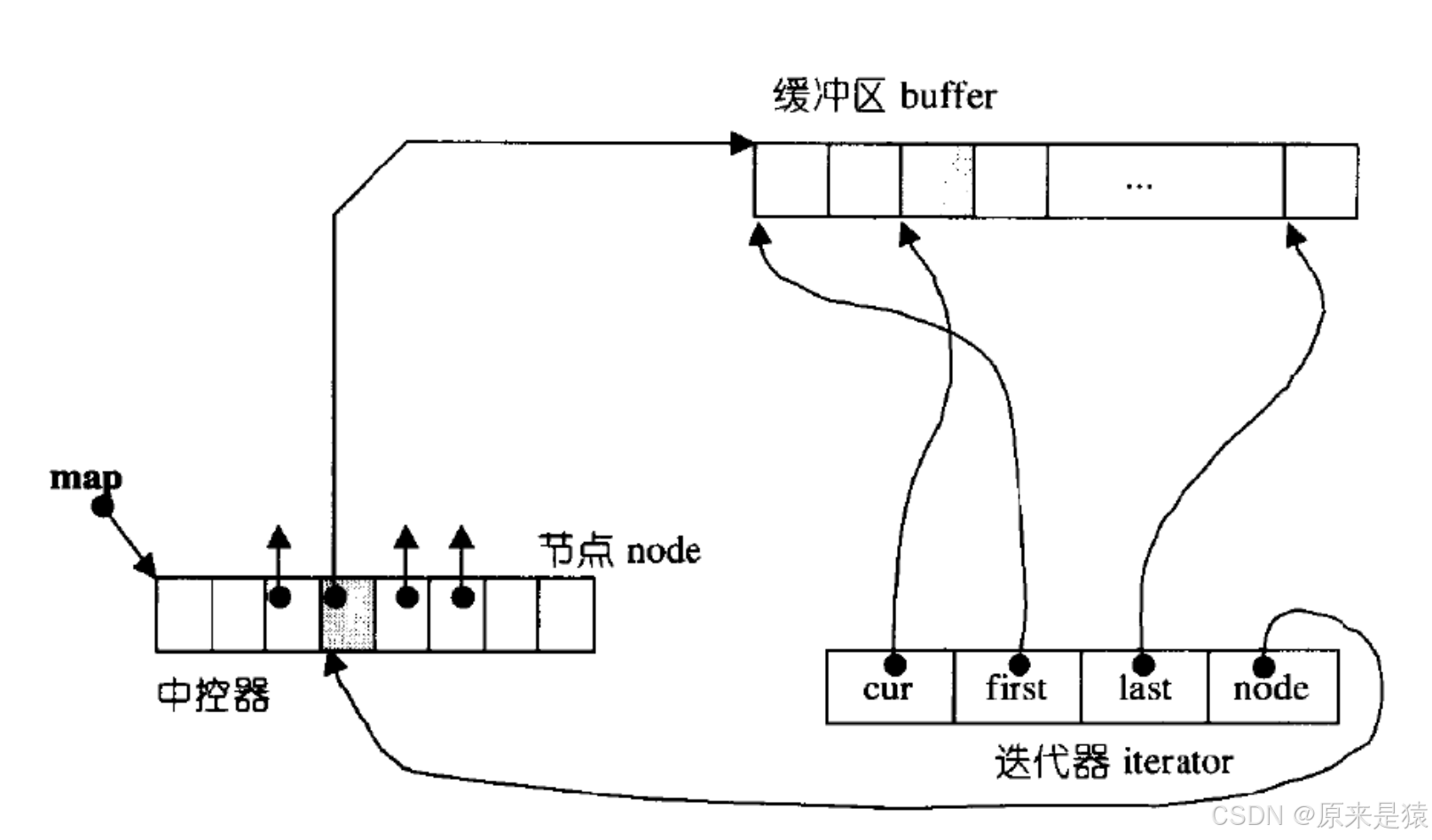
那deque 是如何借助其迭代器維護其假象連續的結構呢？

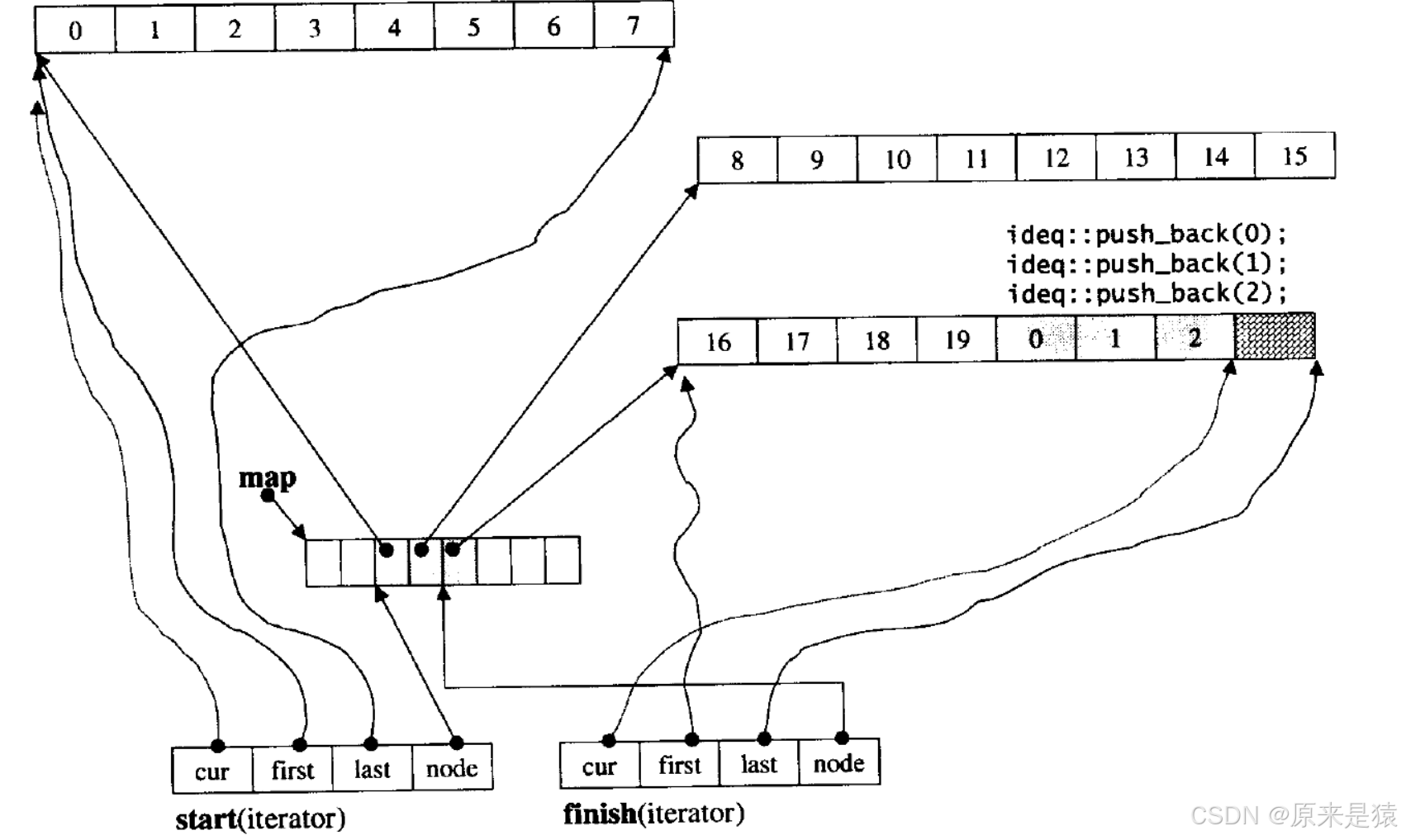
4.2 deque的缺陷

1. 與 vector 比較 ， deque 的優勢是：頭部插入和刪除時候，不需要搬移元素， 效率特別高，而且在擴容時，也不需要搬移大量元素，因此其效率是比 vector 高。

2. 與list 比較，其底層是連續空間，空間利用率比較高，不需要存儲額外字段。

3. 但是， deque有一個致命的缺陷 ：

?不適合遍歷， 因為在遍歷時， deque 的迭代器要頻繁的去檢測其是否移動到某一段小空間的邊界，導致效率低下? ，而序列式場景中，可能需要經常遍歷，因此在實際中，需要線性結構時，大多數情況下優先考慮 vector 和 list , deque 的應用并不多，而目前能看到的一個應用就是， STL用其作為stack 和 queue 的底層結構。

4.3 為什么選擇 deque 作為stack 和 queue的底層默認容器

1 . stack 是一種后進先出的特殊結構，因此只要具有 push_back() 和 pop_back() 操作的線性結構，都可以作為stack的底層容器，比如vector 和 list 都可以 。

2.? queue 是 先進先出的特殊線性數據結構，只要具有 push_back() 和 pop_front() 操作的線性結構，都可以作為 queue的底層容器， 比如 list 。

但是STL中對stack 和 queue 默認選擇 deque 作為底層容器，主要是因為：

1. stack 和 queue不需要遍歷（因此 stack 和 queue沒有迭代器），只需要固定的一端或者兩端進行操作。

2. 在 stack 中元素增長時， deque比vector 的效率高（擴容時不需要搬移大量數據）;queue中的元素增長時， deque不經效率高，而且內存使用率高。

結合了deque的優點，而完美的避開了缺陷

五、priority_queue

priority_queue - C++ Reference

5.1 priority_queue的介紹

1.? 優先隊列是一種? 容器適配器，根據嚴格的弱排序標準，它的第一個元素??總是它所包含的元素中最大的。

2.?此上下文類似于堆，在堆中可以隨時插入元素，并且只能檢索最大堆元素(優先隊列中位于頂部的元素)。

3.?優先隊列被實現為容器適配器，容器適配器即將特定容器類封裝作為其底層容器類，queue提供一組特定的成員函數來訪問其元素。元素從特定容器的“尾部”彈出，其稱為優先隊列的頂部。

5.2 priority_queue的使用

優先級隊列默認使用? vector作為其底層存儲數據的容器，在vector上又使用了堆算法將vector中元素構造成堆的結構，因此priority_queue就是堆，所有需要用到堆的位置，都可以考慮使用 priority_queue。注意：默認情況下priority_queue是大堆。

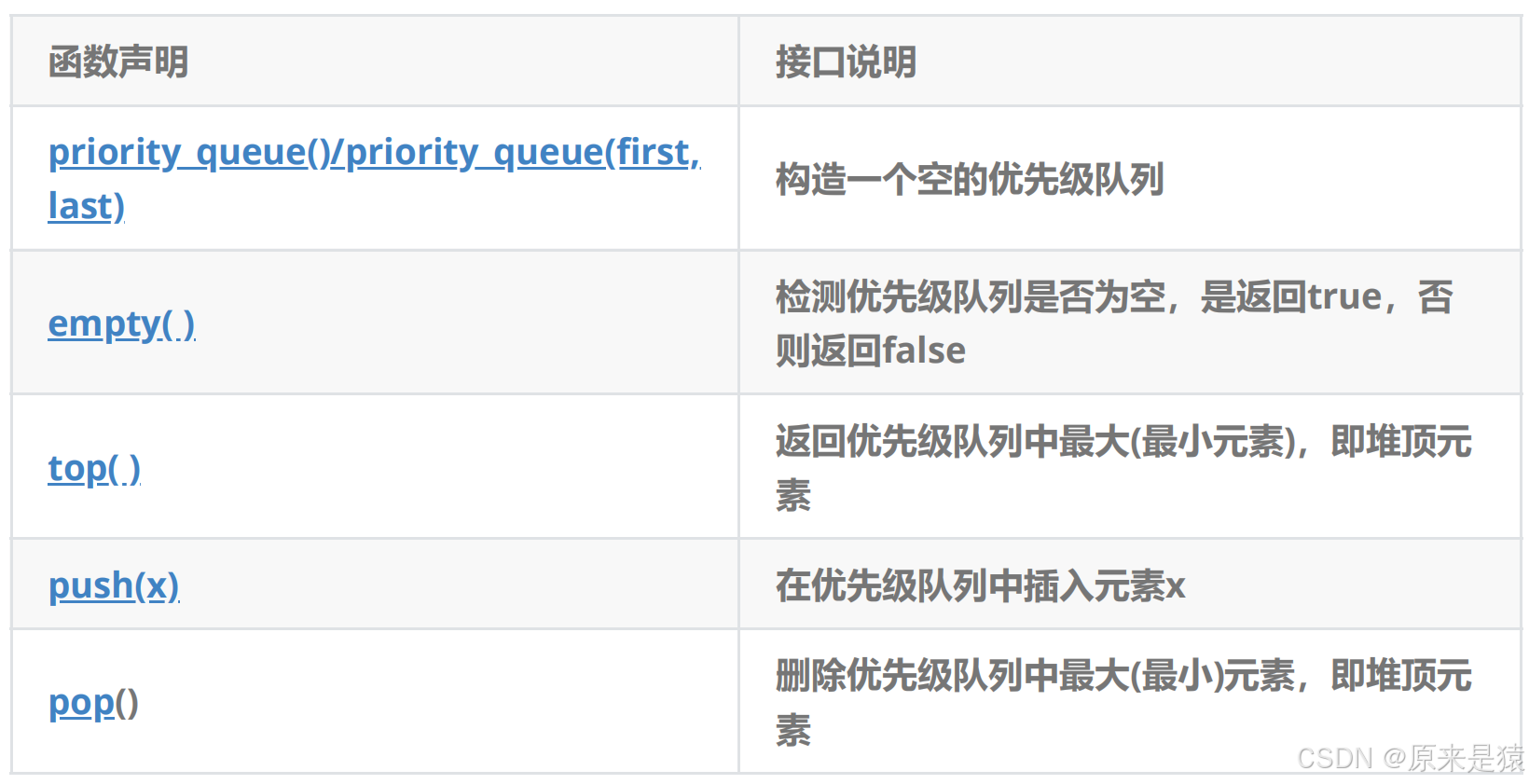
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<queue>
using namespace std;int main()
{
//默認是大的優先級高priority_queue<int> pq;pq.push(15);pq.push(2);pq.push(31);pq.push(4);while (!pq.empty()){cout << pq.top() << " ";pq.pop();}cout << endl;return 0;
}

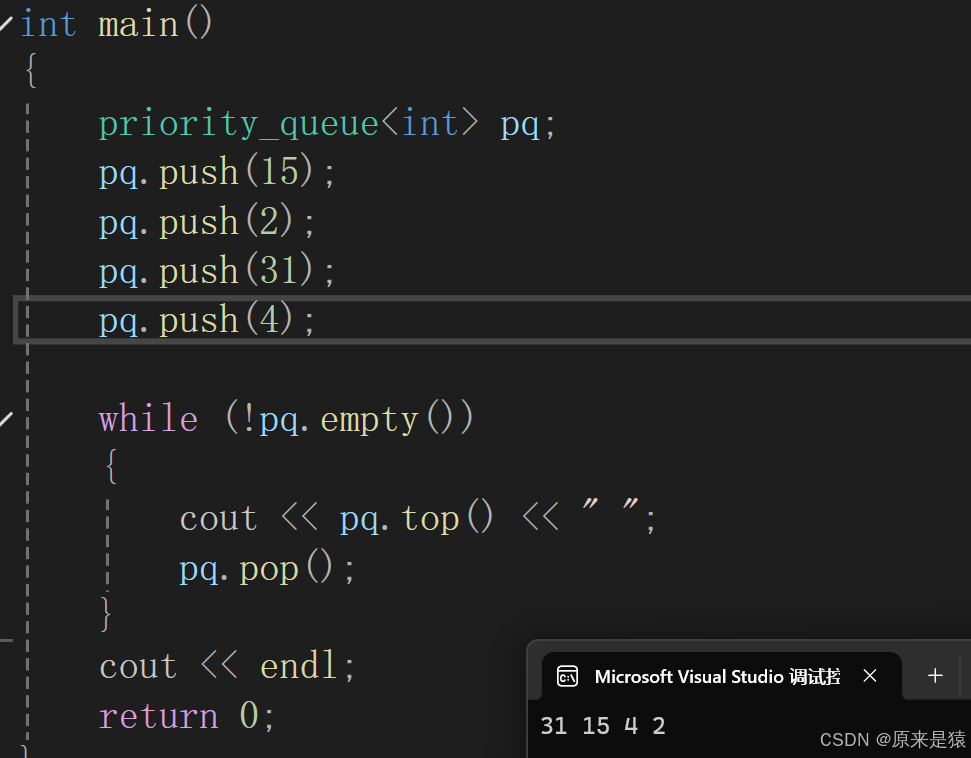
1）數組中第K個大的元素?

?215. 數組中的第K個最大元素 - 力扣（LeetCode）

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {priority_queue<int> p(nums.begin(),nums.end());while(--k){p.pop();} return p.top();}
};

5.3 priority_queue的模擬實現?

#pragma once
#include<vector>namespace bit
{template <class T>struct less {bool operator() (const T& x, const T& y) const{ return x < y;}};template <class T>struct greater{bool operator() (const T& x, const T& y) const{return x > y;}};template<class T, class Container = vector<T>, class Compare = less<T>>class priority_queue{public:// 強制生成priority_queue() = default;template <class InputIterator>priority_queue(InputIterator first, InputIterator last):_con(first, last){// 建堆for (int i = (_con.size()-1-1)/2; i >= 0; i--){AdjustDown(i);}}void AdjustUp(int child){Compare com;int parent = (child - 1) / 2;while (child > 0){//if (_con[parent] < _con[child])if (com(_con[parent], _con[child])){swap(_con[child], _con[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}}void push(const T& x){_con.push_back(x);AdjustUp(_con.size() - 1);}void AdjustDown(int parent){Compare com;size_t child = parent * 2 + 1;while (child < _con.size()){// 假設法，選出左右孩子中小的那個孩子//if (child + 1 < _con.size() && _con[child] < _con[child + 1])if (child + 1 < _con.size() && com(_con[child], _con[child + 1])){++child;}//if (_con[parent] < _con[child])if (com(_con[parent], _con[child])){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0);}bool empty(){return _con.empty();}const T& top(){return _con[0];}size_t size(){return _con.size();}private:Container _con;};
}