卷積神經網絡：模型評估標準

一、分類模型評價指標

在模型評估中，有多個標準用于衡量模型的性能，這些標準包括準確率（Accuracy）、精確率（Precision）、召回率（Recall）、F1 分數（F1-Score）等。

真正例（True Positive, TP）

定義：模型正確地預測為正類的樣本數量。通俗解釋：假設你有一個垃圾郵件分類器，它會把郵件標記為垃圾郵件或非垃圾郵件。真正例就是那些被正確標記為垃圾郵件的郵件數量。

例子：你有 100 封郵件。其中 30 封是垃圾郵件。模型正確地將 25 封垃圾郵件標記為垃圾郵件。那么 TP = 25。

真負例（True Negative, TN）

定義：模型正確地預測為負類的樣本數量。通俗解釋：假設你有一個垃圾郵件分類器，它會把郵件標記為垃圾郵件或非垃圾郵件。真負例就是那些被正確標記為非垃圾郵件的郵件數量。

例子：你有 100 封郵件。其中 70 封是非垃圾郵件。模型正確地將 60 封非垃圾郵件標記為非垃圾郵件。那么 TN = 60。

假正例（False Positive, FP）

定義：模型錯誤地預測為正類的樣本數量。通俗解釋：假設你有一個垃圾郵件分類器，它會把郵件標記為垃圾郵件或非垃圾郵件。假正例就是那些被錯誤地標記為垃圾郵件的非垃圾郵件數量。

例子：你有 100 封郵件。其中 70 封是非垃圾郵件。模型錯誤地將 10 封非垃圾郵件標記為垃圾郵件。那么 FP = 10。

假負例（False Negative, FN）

定義：模型錯誤地預測為負類的樣本數量。通俗解釋：假設你有一個垃圾郵件分類器，它會把郵件標記為垃圾郵件或非垃圾郵件。假負例就是那些被錯誤地標記為非垃圾郵件的垃圾郵件數量。

例子：你有 100 封郵件。其中 30 封是垃圾郵件。模型錯誤地將 5 封垃圾郵件標記為非垃圾郵件。那么 FN = 5。

真正例（TP）：模型正確預測為正類的樣本數量。
真負例（TN）：模型正確預測為負類的樣本數量。
假正例（FP）：模型錯誤預測為正類的樣本數量。
假負例（FN）：模型錯誤預測為負類的樣本數量。

二、準確率（Accuracy）

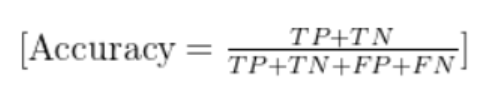
首先，我們需要明確數據的分類情況。這里有 3 個類別（0、1、2），先統計每個類別的預測正確與錯誤情況：

真實標簽?y_true = [2, 0, 2, 2, 0, 1]
預測結果?y_pred = [0, 0, 2, 2, 0, 2]

逐樣本對比：

樣本索引	真實標簽 (y_true)	預測標簽 (y_pred)	結果
0	2	0	錯誤（2→0）
1	0	0	正確（0→0）
2	2	2	正確（2→2）
3	2	2	正確（2→2）
4	0	0	正確（0→0）
5	1	2	錯誤（1→2）

定義：所有預測正確的樣本數占總樣本數的比例。
公式：
Accuracy=總樣本數預測正確的樣本數?

計算：

預測正確的樣本數：樣本 1、2、3、4 → 共 4 個
總樣本數：6 個
準確率 = 4/6 ≈ 0.6667（66.67%）

三、精確率（Precision）

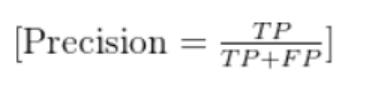
定義：針對某一類別，預測為該類別的樣本中，實際確實是該類別的比例（“預測對的” 占 “預測為該類” 的比例）。
公式（以類別c為例）：
Precision(c)=所有預測為c的樣本數預測為c且真實為c的樣本數?

計算（分類別）：

類別 0：
預測為 0 的樣本：樣本 0、1、4 → 共 3 個
其中真實為 0 的樣本：樣本 1、4 → 共 2 個
精確率 = 2/3 ≈ 0.6667（66.67%）
類別 1：
預測為 1 的樣本：0 個（所有預測中沒有 1）
精確率 = 0（或無定義，因分母為 0）
類別 2：
預測為 2 的樣本：樣本 2、3、5 → 共 3 個
其中真實為 2 的樣本：樣本 2、3 → 共 2 個
精確率 = 2/3 ≈ 0.6667（66.67%）

注：多分類問題中，通常會計算 “宏平均精確率”（各類別精確率的平均值）或 “微平均精確率”（全局統計的精確率）。這里宏平均精確率 = (0.6667 + 0 + 0.6667)/3 ≈ 0.4444（44.44%）。

四、召回率（Recall）

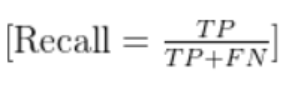
定義：針對某一類別，真實為該類別的樣本中，被成功預測為該類別的比例（“預測對的” 占 “真實為該類” 的比例）。
公式（以類別c為例）：
Recall(c)=所有真實為c的樣本數預測為c且真實為c的樣本數?

計算（分類別）：

類別 0：
真實為 0 的樣本：樣本 1、4 → 共 2 個
其中預測為 0 的樣本：樣本 1、4 → 共 2 個
召回率 = 2/2 = 1（100%）
類別 1：
真實為 1 的樣本：樣本 5 → 共 1 個
其中預測為 1 的樣本：0 個
召回率 = 0/1 = 0（0%）
類別 2：
真實為 2 的樣本：樣本 0、2、3 → 共 3 個
其中預測為 2 的樣本：樣本 2、3 → 共 2 個
召回率 = 2/3 ≈ 0.6667（66.67%）

注：多分類問題中，宏平均召回率 = (1 + 0 + 0.6667)/3 ≈ 0.5556（55.56%）。

五、F1 分數（F1-Score）

定義：精確率和召回率的調和平均數，綜合反映模型的穩健性（避免精確率高但召回率低，或反之）。
公式（以類別c為例）：
F1(c)=2×Precision(c)+Recall(c)Precision(c)×Recall(c)?

計算（分類別）：

類別 0：
F1 = 2 × (0.6667 × 1) / (0.6667 + 1) = 2 × 0.6667 / 1.6667 ≈ 0.8（80%）
類別 1：
F1 = 2 × (0 × 0) / (0 + 0) → 0（因精確率和召回率均為 0）
類別 2：
F1 = 2 × (0.6667 × 0.6667) / (0.6667 + 0.6667) = 2 × 0.4444 / 1.3334 ≈ 0.6667（66.67%）

注：多分類問題中，宏平均 F1 = (0.8 + 0 + 0.6667)/3 ≈ 0.4889（48.89%）。

總結

指標	整體 / 宏平均結果
準確率（Accuracy）	66.67%
精確率（Precision）	44.44%
召回率（Recall）	55.56%
F1 分數（F1-Score）	48.89%

六、混淆矩陣

混淆矩陣是評估分類問題的基礎工具，它是一個表格，顯示了分類算法的預測結果與真實標簽之間的關系。對于二分類問題，混淆矩陣包含真正例（TP）、真負例（TN）、假正例（FP）和假負例（FN）。這些值是計算其他評估指標的基礎。混淆矩陣不僅提供了一個直觀的視覺表示，還允許我們深入了解模型在各個類別上的表現，特別是當處理不平衡數據集時，混淆矩陣可以揭示模型是否傾向于錯誤地將一個類別分類為另一個類別。

混淆矩陣（Confusion Matrix）是機器學習和統計學中評估分類模型性能的重要工具，它以矩陣形式直觀展示模型對各類別的預測結果與真實標簽的匹配情況，能幫助我們深入理解模型的錯誤類型（如將 A 類誤判為 B 類的頻率）。

6.1混淆矩陣的基本結構

混淆矩陣是一個?n×n?的方陣（n?為類別數量），行代表?真實標簽，列代表?預測標簽。每個單元格?(i,j)?表示 “真實標簽為?i?且被預測為?j” 的樣本數量。

以?二分類問題（最常見場景）為例，混淆矩陣為?2×2?結構，核心概念如下：

真實標簽 \ 預測標簽	預測為正例（Positive）	預測為負例（Negative）
正例（Positive）	TP（True Positive）	FN（False Negative）
負例（Negative）	FP（False Positive）	TN（True Negative）

TP：真實為正例，預測也為正例（正確預測）。
FN：真實為正例，卻預測為負例（漏檢，“假陰性”）。
FP：真實為負例，卻預測為正例（誤檢，“假陽性”）。
TN：真實為負例，預測也為負例（正確預測）。

6.2多分類問題的混淆矩陣

對于?n?個類別的分類任務（如識別手寫數字 0-9），混淆矩陣為?n×n?結構，每個單元格?(i,j)?表示 “真實類別為?i?且被預測為?j” 的樣本數。

例如，用本文開頭的三分類數據（類別 0、1、2）：

ytrue?=[2,0,2,2,0,1]
ypred?=[0,0,2,2,0,2]

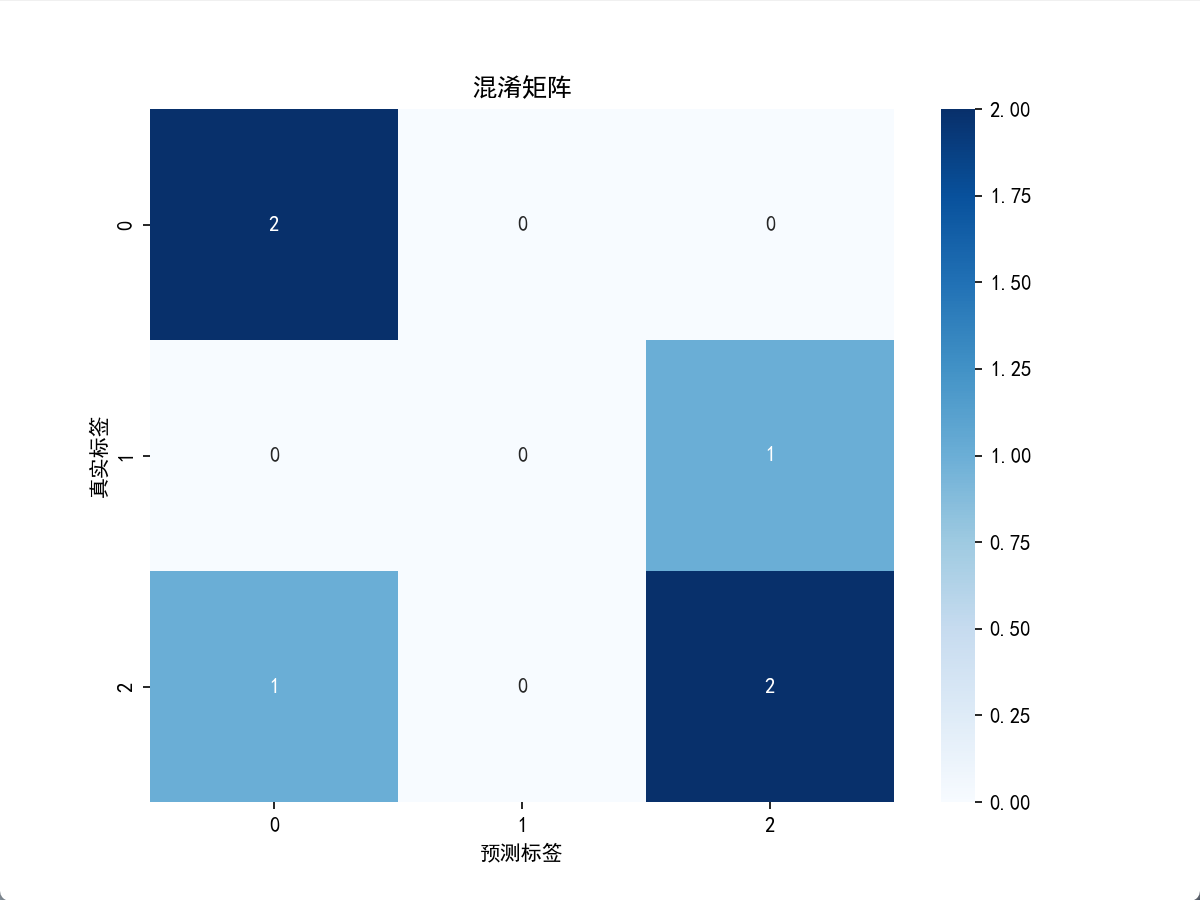
其混淆矩陣為?3×3：

真實標簽 \ 預測標簽	預測 0	預測 2
真實 0	2	0
真實 1	0	1
真實 2	1	2

對角線（如真實 0→預測 0、真實 2→預測 2）表示預測正確的樣本數，總和為模型正確預測的總樣本數。
非對角線（如真實 2→預測 0、真實 1→預測 2）表示預測錯誤的樣本數，可直觀看到模型容易將哪些類別混淆。

6.3混淆矩陣的核心作用

計算評估指標
幾乎所有分類指標（準確率、精確率、召回率、F1 分數等）都可通過混淆矩陣推導：
- 準確率（Accuracy）：TP+TN+FP+FNTP+TN?（整體正確率）
- 精確率（Precision）：TP+FPTP?（預測為正例中真正為正例的比例）
- 召回率（Recall）：TP+FNTP?（真實正例中被正確預測的比例）
- F1 分數：2×Precision+RecallPrecision×Recall?（精確率和召回率的調和平均）
分析錯誤模式
混淆矩陣能揭示模型的 “薄弱環節”，例如：
- 在圖像分類中，模型是否經常將 “貓” 誤判為 “狗”？
- 在疾病診斷中，是否有大量 “真陽性” 被漏檢（FN 過高）？
指導模型優化
根據錯誤模式調整模型：若某類別的 FN 過高（召回率低），可增加該類樣本的訓練數據；若某類別的 FP 過高（精確率低），可優化特征以減少誤判。

6.4如何繪制混淆矩陣？

在 Python 中，可使用?scikit-learn?生成混淆矩陣，再用?matplotlib?或?seaborn?可視化：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import confusion_matrixplt.rcParams['font.sans-serif'] = ['SimHei'] #用來正常顯示中文標簽
plt.rcParams['axes.unicode_minus'] = False #用來正常顯示負號# 示例數據
y_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])
classes = [0, 1, 2]  # 類別標簽# 計算混淆矩陣
cm = confusion_matrix(y_true, y_pred)# 可視化
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=classes, yticklabels=classes)
plt.xlabel('預測標簽')
plt.ylabel('真實標簽')
plt.title('混淆矩陣')
plt.show()

from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score,f1_score
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 假設我們有以下真實標簽和預測結果
y_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])# 計算準確率
accuracy = accuracy_score(y_true, y_pred)
print("準確率：", accuracy)# 計算精確率
precision = precision_score(y_true, y_pred, average='macro')
print("精確率：", precision)# 計算召回率
recall = recall_score(y_true, y_pred, average='macro')
print("召回率：", recall)# 計算F1分數
f1 = f1_score(y_true, y_pred, average='macro')
print("F1分數：", f1)# 計算混淆矩陣
cm = confusion_matrix(y_true, y_pred)# 使用Seaborn的heatmap函數來可視化混淆矩陣
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.title('Confusion Matrix')
plt.show()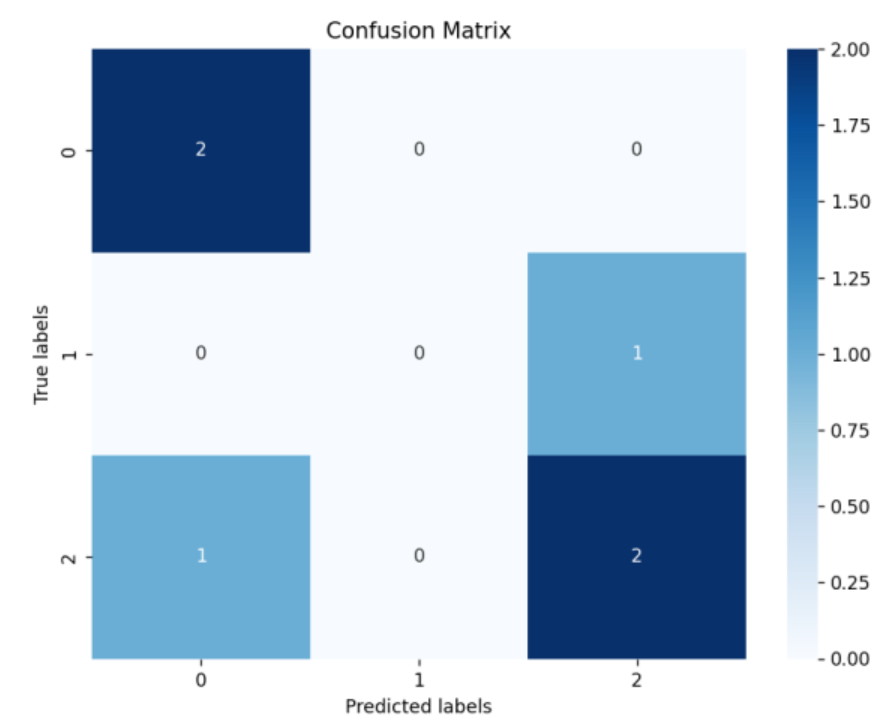

運行后會生成帶數值標注的熱力圖，顏色越深表示該單元格的樣本數越多，直觀展示分類結果。

6.5總結

混淆矩陣是分類模型評估的 “基石”，它不僅能幫助計算各類量化指標，更能通過可視化直觀呈現模型的錯誤分布，為模型優化提供具體方向。無論是二分類還是多分類問題，理解混淆矩陣都是數據分析和機器學習中的必備技能。

七、ROC曲線和AUC值（不怎么用）

ROC曲線是一個性能度量，顯示了在不同閾值設置下模型的真正例率（召回率）和假正例率的關系。AUC值表示ROC曲線下的面積，用于衡量模型的整體性能，AUC值越高，模型性能越好。ROC曲線和AUC值是評估模型區分不同類別能力的重要工具，尤其在二分類問題中非常實用。

7.1ROC 曲線的基本概念

ROC 曲線以假正例率（False Positive Rate, FPR）?為橫軸，以真正例率（True Positive Rate, TPR）?為縱軸，描述了模型在不同閾值下的分類性能。

1. 核心指標定義

真正例率（TPR，又稱靈敏度、召回率）：
真實正例中被正確預測為正例的比例，反映模型對正例的識別能力。
TPR=TP+FNTP?
假正例率（FPR，又稱 1 - 特異度）：
真實負例中被錯誤預測為正例的比例，反映模型的誤判率。
FPR=FP+TNFP?
（注：TP、TN、FP、FN 的定義見混淆矩陣相關內容）

2. ROC 曲線的繪制邏輯

分類模型（如邏輯回歸、SVM 等）通常會輸出樣本屬于正例的概率分數（而非直接輸出類別）。通過調整分類閾值（如將概率≥0.5 的樣本判為正例），可得到不同的 TPR 和 FPR：

閾值越低：更多樣本被預測為正例，TPR 升高（識別更多正例），但 FPR 也升高（誤判更多負例）。
閾值越高： fewer 樣本被預測為正例，FPR 降低（誤判減少），但 TPR 也降低（可能漏檢正例）。

ROC 曲線通過遍歷所有可能的閾值，計算對應的 (TPR, FPR) 點并連接而成，完整反映模型在 “靈敏度 - 特異度” 權衡下的整體表現。

7.2ROC 曲線的解讀

理想模型：
當閾值調整時，能 100% 識別正例（TPR=1）且 0 誤判負例（FPR=0），ROC 曲線會直接從 (0,0) 垂直上升到 (0,1)，再水平向右到 (1,1)，形成一個直角。
隨機猜測模型：
若模型無預測能力（如隨機猜測），TPR 與 FPR 相等，ROC 曲線為一條從 (0,0) 到 (1,1) 的對角線（斜率 = 1）。
實際模型：
好的模型 ROC 曲線應盡可能靠近左上角（高 TPR、低 FPR），且整體在隨機猜測的對角線上方。兩條 ROC 曲線比較時，上方的曲線對應性能更優的模型。

7.3AUC 值（曲線下面積）

AUC 是 ROC 曲線與橫軸之間的面積，取值范圍為?[0, 1]，用于量化評估模型的整體性能。

1. AUC 的物理意義

AUC=1：完美模型，能完全區分正負例（TPR=1 且 FPR=0）。
AUC=0.5：模型性能與隨機猜測相同（如拋硬幣）。
AUC<0.5：模型性能差于隨機猜測（實際應用中可反向預測改善）。
AUC 越接近 1：模型區分正負例的能力越強。

更直觀地說，AUC 表示 “隨機抽取一個正例和一個負例，模型將正例預測為正例的概率高于負例的概率” 的可能性。例如，AUC=0.8 意味著有 80% 的概率，模型能正確區分隨機選取的正負例。

2. AUC 的優勢

對閾值不敏感：ROC 曲線和 AUC 綜合了所有閾值下的表現，避免了單一閾值的局限性。
適用于不平衡數據：在正負樣本比例懸殊時（如疾病數據中患者僅占 1%），AUC 比準確率（Accuracy）更能反映模型真實性能（準確率可能因多數類占優而虛高）。

7.4如何計算和繪制 ROC 曲線與 AUC？

在 Python 中，可使用scikit-learn快速實現：

from sklearn.metrics import roc_curve, roc_auc_score
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import matplotlib.pyplot as plt
import numpy as npplt.rcParams['font.sans-serif'] = ['SimHei'] #用來正常顯示中文標簽
plt.rcParams['axes.unicode_minus'] = False #用來正常顯示負號# 假設我們有一個數據集
X = np.array([[0, 0], [1, 1], [2, 0], [2, 2], [0, 1]])
y = np.array([1, 1, 0, 1, 0])plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red', label='Class 0')
plt.scatter(X[y == 1, 0], X[y == 1, 1], color='blue', label='Class 1')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.title('Data Points by Class')
plt.grid(True)
plt.show()# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42)print("--------訓練樣本-----------")
print(X_train,y_train)
print("--------測試樣本-----------")
print(X_test,y_test)# 訓練一個隨機森林分類器
clf = RandomForestClassifier(n_estimators=100, random_state=42)
clf.fit(X_train, y_train)# 預測概率
y_scores = clf.predict_proba(X_test)[:, 1]# 計算ROC曲線和AUC值
fpr, tpr, thresholds = roc_curve(y_test, y_scores)
auc = roc_auc_score(y_test, y_scores)# 繪制ROC曲線
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正例率')
plt.ylabel('真正例率')
plt.title('ROC曲線')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()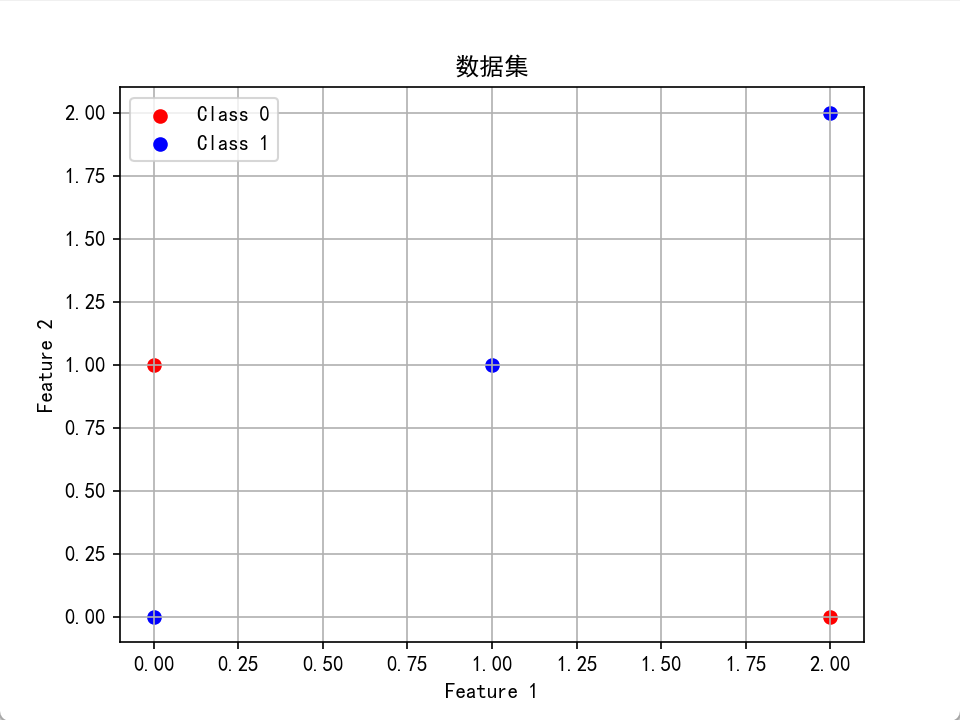

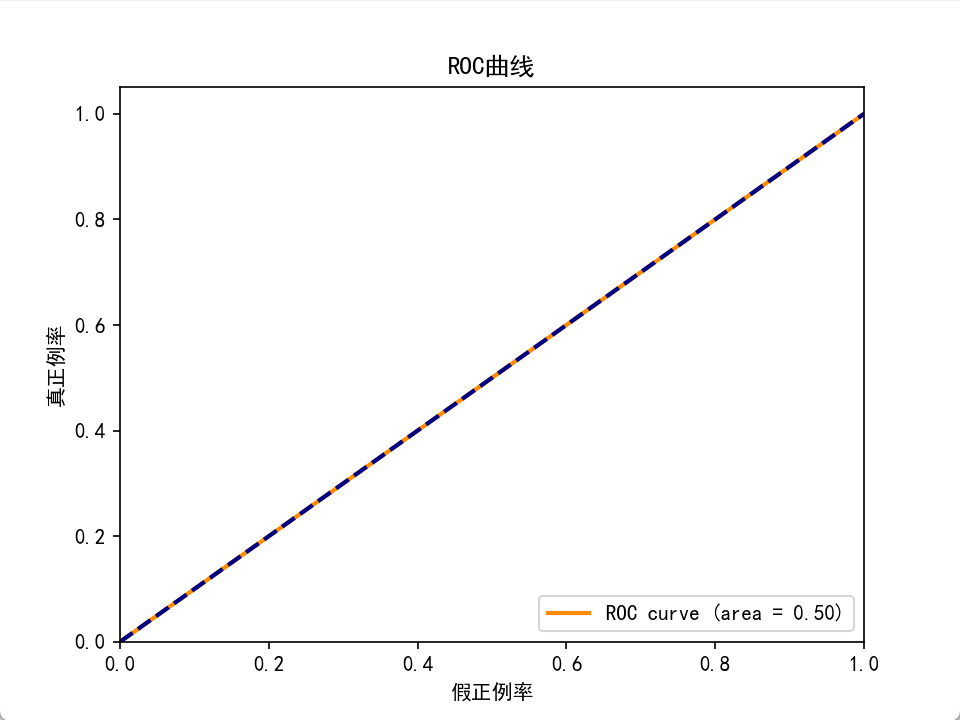
運行結果會顯示一條 ROC 曲線和對應的 AUC 值，直觀反映模型性能。

7.5注意事項

多分類問題：ROC 曲線本質是二分類工具，多分類場景需通過 “一對多”（One-vs-Rest）或 “一對一”（One-vs-One）策略轉化為多個二分類問題，再計算平均 AUC。
數據不平衡的局限性：雖然 AUC 對不平衡數據的魯棒性優于準確率，但當負例數量極多時，FPR 的微小變化可能被放大，需結合精確率 - 召回率曲線（PR 曲線）綜合評估。
閾值選擇：AUC 反映整體性能，但實際應用中需根據業務需求選擇閾值（如疾病診斷更關注高召回率以減少漏診，垃圾郵件過濾更關注高精確率以減少誤判）。