Fast Frequency Estimation Algorithm by Least Squares Phase Unwrapping

I. 引言

單個含噪正弦信號的頻率估計是一個研究已久的問題，并有多種應用[1]。在高斯白噪聲假設下，最大似然(ML)頻率估計器是Rife和Boorstyn [2]中提出的周期圖估計器，其中傅里葉變換用于搜索周期圖的最大值。周期圖估計器被廣泛認為是單頻估計的最佳方法。在[2]中，粗略搜索基于快速傅里葉變換(FFT)，而精細搜索則基于非線性優化。為了簡化非線性優化，[3]中研究了一種五峰值內插器，它可以找到峰值并產生接近ML估計器的估計。此外，信號子空間法(SA)也已用于估計單個含噪正弦信號的頻率[4]，其中頻率估計在小誤差條件下近似無偏，其方差接近ML估計器的方差。

相位展開估計器是另一種單頻估計方法，最早在[5]中提出。該方法展開復正弦信號的相位，然后通過線性回歸（linear regression，LR）估計頻率。然而，傳統的相位展開算法在低信噪比(SNR)下會遇到模 $2π2\pi$ 模糊問題，以至于相位展開估計器的閾值處于相對較高的SNR [6]。

為了解決模 $2π2\pi$ 模糊問題，Clarkson將相位展開問題轉化為尋找格中的最近點，并利用格點理論解決了該問題[7]。仿真結果表明，其估計性能接近周期圖估計器，但作者沒有提供理論證明。最近，McKilliam在最小二乘意義上發展了基于格的方法[8]，并證明了該估計器是強一致的，其估計方差在數值模擬中的高信噪比下接近克拉默-拉奧界(CRB) [2]。在[8]中，最小二乘相位展開估計器(LSPUE)顯示出與經典周期圖估計器相同的閾值。然而，基于格點理論的相位展開具有高達 $O(N^3\log N)$ 的計算復雜度，因此不能用于實際應用。最近，有人提出了一種基于相位濾波器的快速相位展開方法[9]，但是在頻率估計問題中濾波器參數很難確定。

在這封信中，我們提出了一種快速頻率估計算法，它結合了LSPUE的準確性和濾波方法的快速操作。所提出的方法在最小二乘意義上執行相同的相位展開，因此它具有與[8]中方法相同的性能，但計算復雜度低至 $O(N^2)$ 。

II. PROBLEM DESCRIPTION

假設觀測到的包含 $N$ 個樣本的序列具有以下形式：

$r_n = Ae^{j2\pi(fn+\theta)} + w_n, \quad n=0, 1, \dots, N-1 \quad \tag{1}$

其中 $f$ 是頻率， $θ\theta$ 是初始相位， $A$ 是信號幅度。噪聲樣本 $w_n$ 是獨立的、同分布的高斯復隨機變量，均值為0，方差為 $2σ22\sigma^2$ 。在這封信中，我們試圖估計頻率 $f$ ，并假設 $f$ 在 $[? 1/2, 1/2)$ 范圍內。 $r_n$ 的相位由下式給出：

$\angle r_n = 2\pi(fn + \theta + v_n) \quad (\text{mod } 2\pi) \quad \tag{2}$

其中 $v_n$ 是在 $[? 1/2, 1/2)$ 范圍內定義的相位噪聲。噪聲項 $v_n$ 的分布如下[10]：

$f_v(x) = e^{-\gamma} + 2\sqrt{\pi\gamma}\cos{2\pi x}e^{-\gamma\sin^2{2\pi x}}Q(-\sqrt{2\gamma}\cos{2\pi x}) \quad \tag{3}$

其中 $γ=A22σ2\gamma = \frac{A^2}{2\sigma^2}$ 是信噪比(SNR)。Q函數定義為：

$\int_x^\infty \phi(t)dt \quad \tag{4}$

其中

$\phi(t) = \frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}} \quad \tag{5}$

是標準正態分布。對于 $x > 0$ ，我們有

$\int_x^\infty \phi(t)dt < \int_x^\infty \frac{t}{x}\phi(t)dt = \frac{\phi(x)}{x}$

$∫x∞tx?(t)dt=1x∫x∞t??(t)dt=1x∫x∞t?12πe?t22dt=1x2π∫x∞te?t22dt=1x2π∫?x2/2?∞eu(?du)(令?u=?t2/2,?則?du=?t?dt)=1x2π∫?∞?x2/2eudu=1x2π[eu]?∞?x2/2=1x2π(e?x2/2?lim?a→?∞ea)=1x2π(e?x2/2?0)=1x(12πe?x2/2)=?(x)x\begin{align*} \int_x^\infty \frac{t}{x}\phi(t)dt &= \frac{1}{x} \int_x^\infty t \cdot \phi(t) dt \\ &= \frac{1}{x} \int_x^\infty t \cdot \frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}} dt \\ &= \frac{1}{x \sqrt{2\pi}} \int_x^\infty t e^{-\frac{t^2}{2}} dt \\ &= \frac{1}{x \sqrt{2\pi}} \int_{-x^2/2}^{-\infty} e^u (-du) \quad (\text{令 } u = -t^2/2, \text{ 則 } du = -t \cdot dt) \\ &= \frac{1}{x \sqrt{2\pi}} \int_{-\infty}^{-x^2/2} e^u du \\ &= \frac{1}{x \sqrt{2\pi}} \left[ e^u \right]_{-\infty}^{-x^2/2} \\ &= \frac{1}{x \sqrt{2\pi}} \left( e^{-x^2/2} - \lim_{a \to -\infty} e^a \right) \\ &= \frac{1}{x \sqrt{2\pi}} \left( e^{-x^2/2} - 0 \right) \\ &= \frac{1}{x} \left( \frac{1}{\sqrt{2\pi}} e^{-x^2/2} \right) \\ &= \frac{\phi(x)}{x} \end{align*}$

并且

$\left(1+\frac{1}{x^2}\right)Q(x) > \int_x^\infty \left(1+\frac{1}{t^2}\right)\phi(t)dt = \frac{\phi(x)}{x}.$

$∫x∞(1+1t2)?(t)dt=∫x∞(?ddt(?(t)t))dt=?[?(t)t]x∞=?(lim?t→∞?(t)t??(x)x)=?(lim?t→∞e?t2/2t2π??(x)x)=?(0??(x)x)=?(x)x\begin{align*} \int_x^\infty \left(1+\frac{1}{t^2}\right) \phi(t) dt &= \int_x^\infty \left(-\frac{d}{dt}\left(\frac{\phi(t)}{t}\right)\right) dt \\ &= -\left[ \frac{\phi(t)}{t} \right]_x^\infty \\ &= -\left( \lim_{t\to\infty} \frac{\phi(t)}{t} - \frac{\phi(x)}{x} \right) \\ &= -\left( \lim_{t\to\infty} \frac{e^{-t^2/2}}{t\sqrt{2\pi}} - \frac{\phi(x)}{x} \right) \\ &= -\left( 0 - \frac{\phi(x)}{x} \right) \\ &= \frac{\phi(x)}{x} \end{align*}$

因此，

$\frac{x}{1+x^2}\phi(x) < Q(x) < \frac{\phi(x)}{x}, \quad x>0. \quad \tag{6}$

考慮到 $Q (x) = 1 ? Q (? x)$ ，我們有

$1+\frac{\phi(x)}{x} < Q(x) < 1+\frac{x}{1+x^2}\phi(x), \quad x<0. \quad \tag{7}$

將(6)和(7)代入(3)，我們發現對于較大的 $γ\gamma$ ， $f_v(x)$ 的下界和上界近似相等。在這種情況下，

$f_v(x) = \begin{cases} 2\sqrt{\pi\gamma}\cos{2\pi x}e^{-\gamma\sin^2{2\pi x}}, & |x| \le 1/4 \\ 0, & |x| > 1/4. \end{cases} \quad \tag{8}$

令 $xn=∠rn/(2π)x_n = \angle r_n / (2\pi)$ ，我們得到

$x_n = fn + \theta + v_n - u_n \quad \tag{9}$

其中 $un=[fn+θ+vn]u_n = [fn + \theta + v_n]$ ， $[x]$ 表示與 $x$ 最接近的整數。因此，我們有

$v_n = x_n + u_n - fn - \theta. \quad \tag{10}$

為了在最小二乘意義上使噪聲項 $v_n$ 最小，我們定義目標函數為

$\theta, u_n) = \sum_{n=0}^{N-1}(x_n + u_n - fn - \theta)^2 \quad \tag{11}$

III. FAST LSPUE ALGORITHM

為了最小化 $\theta, u_n)$ ，困難在于 $u_n$ 是未知的。如果 $u_n$ 已知，我們可以很容易地用最小二乘法公式解決這個問題。在頻率估計問題中，我們發現 $u_n$ 是 $n$ 的單調函數。具體來說，當 $f > 0$ 時， $u_n$ 是單調遞增函數，當 $f < 0$ 時， $u_n$ 是單調遞減函數。考慮到 $\in [-1/2, 1/2)$ ，我們有 $?N2≤f(N?1)+θ<N2-\frac{N}{2} \le f(N-1)+\theta < \frac{N}{2}$ 。因此，我們定義

$u_n^m = \left\lceil m\frac{n}{N} \right\rceil, \quad m = -\frac{N}{2}, -\left(\frac{N}{2}-1\right), \dots, \frac{N}{2}-1. \quad \tag{17}$

對于給定的 $m$ ， $um=[u0m,u1m,…,uN?1m]T\boldsymbol u^m = [u_0^m, u_1^m, \dots, u_{N-1}^m]^T$ 是一個在整數空間 $ZN\mathbb Z^N$ 中的向量。顯然， $um\boldsymbol u^m$ 對應于頻率為 $mN\frac{m}{N}$ 的信號。我們定義 $N$ 個向量，它們代表了 $ZN\mathbb Z^N$ 中最有可能的 $N$ 個解。我們首先檢查這 $N$ 個解，然后在這些 $N$ 個解附近尋找更好的解。整個過程類似于[2]中描述的粗略搜索和精細搜索，但我們是在展開的相位中搜索最佳的 $u_n$ ，而[2]中的算法是在頻域中搜索最大值。

現在，我們重新定義目標函數

$J^m(f, \theta) = \sum_{n=0}^{N-1}(y_n^m - fn - \theta)^2 \quad \tag{18}$

其中

$y_n^m = x_n + u_n^m \quad \tag{19}$

是 $x_n$ 的展開相位。由于 $u_n^m$ 是已知的，由[11]可得頻率和相位

$\frac{12 \sum_{n=0}^{N-1}(n - (N-1)/2)y_n^m}{N(N-1)(N+1)} \quad \tag{20}$

$\theta(m) = \frac{2 \sum_{n=0}^{N-1}(2N-3n-1)y_n^m}{N(N+1)}.$

殘差誤差表示為 $Jm(f(m),θ(m))J^m(f(m), \theta(m))$ 。這是粗略搜索過程。顯然， $f (m)$ 和 $θ(m)\theta(m)$ 是給定 $um\boldsymbol u^m$ 的最佳解，但它們不是全局最優解。現在，我們嘗試在 $um\boldsymbol u^m$ 附近找到更好的解。這是精細搜索過程。首先，我們重構線性相位

$p_n = f(m)n + \theta(m). \quad \tag{21}$

然后，我們圍繞線性相位 $p_n$ 展開相位 $x_n$ ，如下所示

$y^nm=pn+M[xn?pn](22) \hat{y}_n^m = p_n + M[x_n - p_n] \quad \tag{22}$

其中

$\begin{cases} M[X-1], & X > 1/2 \\ M[X+1], & X < -1/2 \\ X, & \text{otherwise}. \end{cases}$

在[9]中研究了(22)中的相位展開操作。這樣， $y^nm\hat{y}_n^m$ 和 $x_n$ 滿足 $y^nm=xn(mod1)\hat{y}_n^m = x_n \pmod 1$ 和 $∣y^nm?pn∣<1/2|\hat{y}_n^m - p_n| < 1/2$ ，這意味著 $y^nm\hat{y}_n^m$ 是 $x_n$ 圍繞 $p_n$ 的相位展開。現在，我們重新定義目標函數

$J^m(f,θ)=∑n=0N?1(y^nm?fn?θ)2.(23) \hat{J}^m(f, \theta) = \sum_{n=0}^{N-1}(\hat{y}_n^m - fn - \theta)^2. \quad \tag{23}$

同樣，我們通過最小二乘法公式求解頻率和相位

$f^(m)=12∑n=0N?1(n?(N?1)/2)y^nmN(N?1)(N+1)(24) \hat{f}(m) = \frac{12 \sum_{n=0}^{N-1}(n - (N-1)/2)\hat{y}_n^m}{N(N-1)(N+1)} \quad \tag{24}$

$θ^(m)=2∑n=0N?1(2N?3n?1)y^nmN(N+1). \hat{\theta}(m) = \frac{2 \sum_{n=0}^{N-1}(2N-3n-1)\hat{y}_n^m}{N(N+1)}.$

殘差誤差表示為 $J^m(f^(m),θ^(m))\hat{J}^m(\hat{f}(m), \hat{\theta}(m))$ 。現在，我們比較殘差誤差 $Jm(f(m),θ(m))J^m(f(m), \theta(m))$ 和 $J^m(f^(m),θ^(m))\hat{J}^m(\hat{f}(m), \hat{\theta}(m))$ 。如果

$Jm(f(m),θ(m))≤J^m(f^(m),θ^(m)) J^m(f(m), \theta(m)) \le \hat{J}^m(\hat{f}(m), \hat{\theta}(m))$

則 $Jm(f(m),θ(m))J^m(f(m), \theta(m))$ 是給定 $m$ 的局部最優解，精細搜索結束。如果

$Jm(f(m),θ(m))>J^m(f^(m),θ^(m)) J^m(f(m), \theta(m)) > \hat{J}^m(\hat{f}(m), \hat{\theta}(m))$

我們按如下方式更新參數：

$f(m)=f^(m)θ(m)=θ^(m)Jm(f(m),θ(m))=J^m(f^(m),θ^(m)) \begin{aligned} f(m) &= \hat{f}(m) \\ \theta(m) &= \hat{\theta}(m) \\ J^m(f(m), \theta(m)) &= \hat{J}^m(\hat{f}(m), \hat{\theta}(m)) \end{aligned}$

然后重復從(21)到(24)的步驟。

同樣地，我們計算所有 $m$ 的殘差誤差 $Jm(f(m),θ(m))J^m(f(m), \theta(m))$ ，并按如下方式找到最優的 $m$ ：

$m^* = \arg \min J^m(f(m), \theta(m)). \quad \tag{25}$

圖1顯示了整個算法的示意圖。圖1(a)顯示了粗略搜索的流程，圖1(b)顯示了精細搜索的流程。顯然，粗略搜索中有 $N$ 個循環，每個循環都包含一次用于尋找局部最優解的精細搜索。根據我們的數值模擬結果，每次精細搜索包含的迭代過程通常在五到八輪后收斂。在每次迭代中，相位展開和最小二乘計算需要 $O (N)$ 次算術運算。因此，整個FLSPUE算法的計算復雜度為 $O(N^2)$ 。

IV. SIMULATION RESULTS

在本節中，我們檢驗在第三節中開發的FLSPUE算法的性能。由于所提出的FLSPUE算法是LSPUE方案的一種快速實現，其性能應與[8]中的LSPUE相同。因此，我們僅比較了五種估計器的性能：ML估計器[2]、快速近似ML估計器（fast ML）[3]、SA[4]、LR[5]以及所提出的FLSPUE算法。理想的ML估計器是搜索周期圖的最大值，但[2]中的非線性優化很復雜。在本信中，我們通過chirp z變換（CZT）算法[12]執行精細搜索，該算法計算由粗略搜索找到的峰值附近的離散傅里葉變換。然后，我們可以從CZT算法的計算結果中搜索最大值。CZT算法是基于FFT實現的，因此基于CZT的ML估計器的計算復雜度仍然是 $\log N$ 。

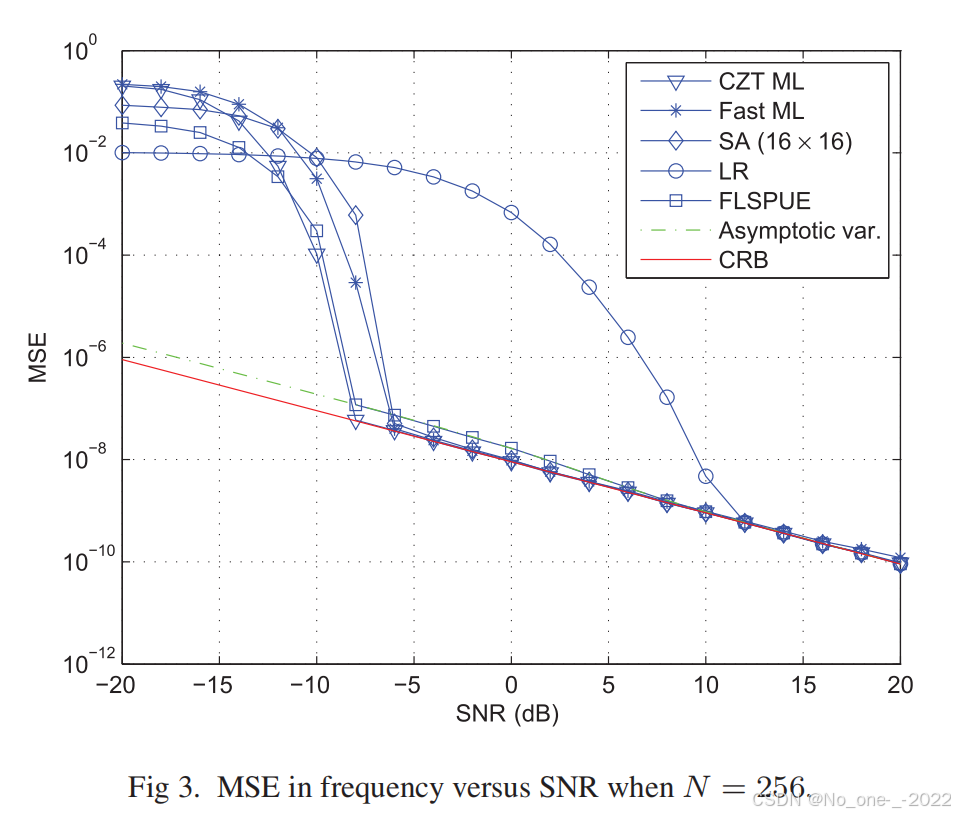
在這里插入圖片描述

在我們的仿真中，單正弦信號的參數為 $f = 0.1$ 和 $θ=0\theta=0$ 。當 $N = 64$ 和 $N = 256$ 時的仿真結果顯示在圖2和圖3中，每次仿真的信噪比(SNR)在–20和20 dB之間變化，每個SNR值都運行了10 000次試驗。在圖2和圖3中，基于CZT的ML估計器被稱為CZT ML。在SA算法中，觀測信號表示為一個 $\times n$ 的數據矩陣，且SA算法在不同矩陣維度下的性能是不同的。在這封信中，我們為 $N = 64$ 選擇 $\times 8$ 的矩陣，為 $N = 256$ 選擇 $16 \times 16$ 的矩陣，因為使用這些參數可以獲得最佳的閾值性能。