考試范圍
一:
- 事件關系運算
- 性質
- 全概率公式、貝葉斯公式
- 古典概型
二:
- 離散分布律
- 連續密度函數性質 -> 解決三個問題(求待定系數、求概率、求密度函數)
- 分布函數 -> 解決三個問題
- 常用分布(最后一節課的那幾個分布)
三:
- 離散(連續)型七個問題:(分布律(確定系數))、概率、邊緣分布(密度)、獨立性、條件分布(密度)、函數分布、協方差(相關系數)
四:
- 數學期望、方差(計算、常用分布、分析)
- 切比雪夫不等式
- 二維 - 兩個變量的相關性和獨立性、協方差
五:
- 中心極限定理
第一課
1.1 無放回類題目(古典概型)



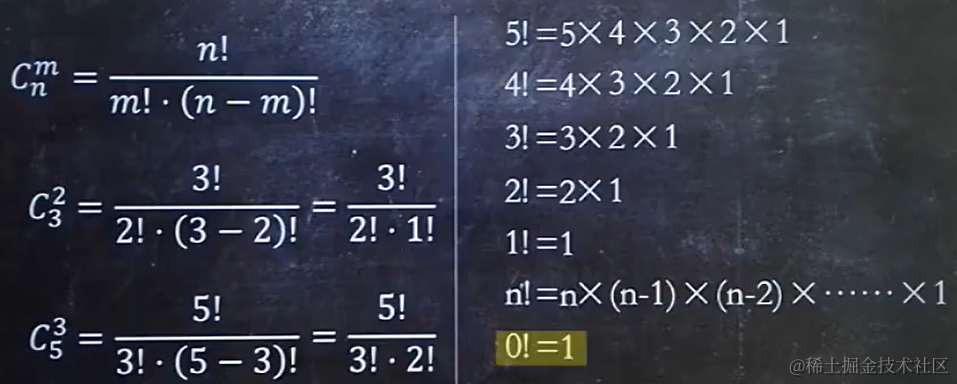
1.2 有放回類題目

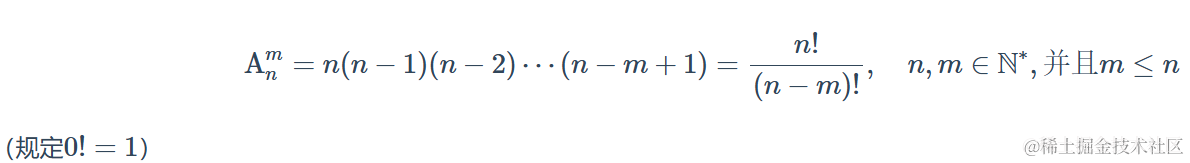
1.3 需要畫圖的題目
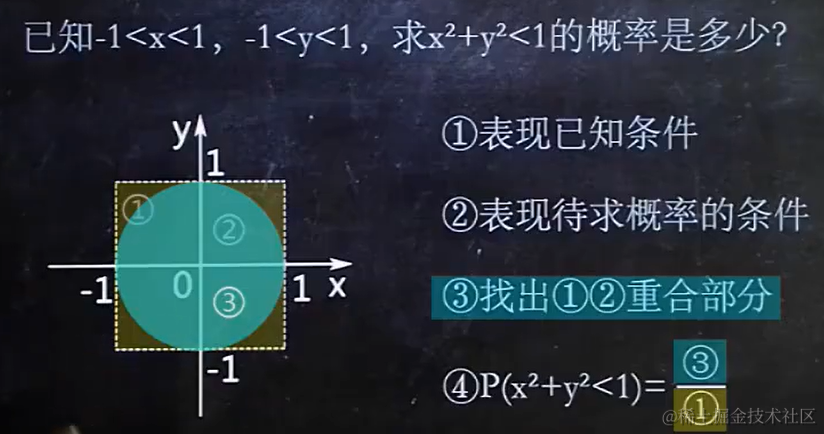
1.4 全概率公式
相互獨立的兩個事件 A 和 B,同時發生的概率是 P(AB) = P(A) * P(B)
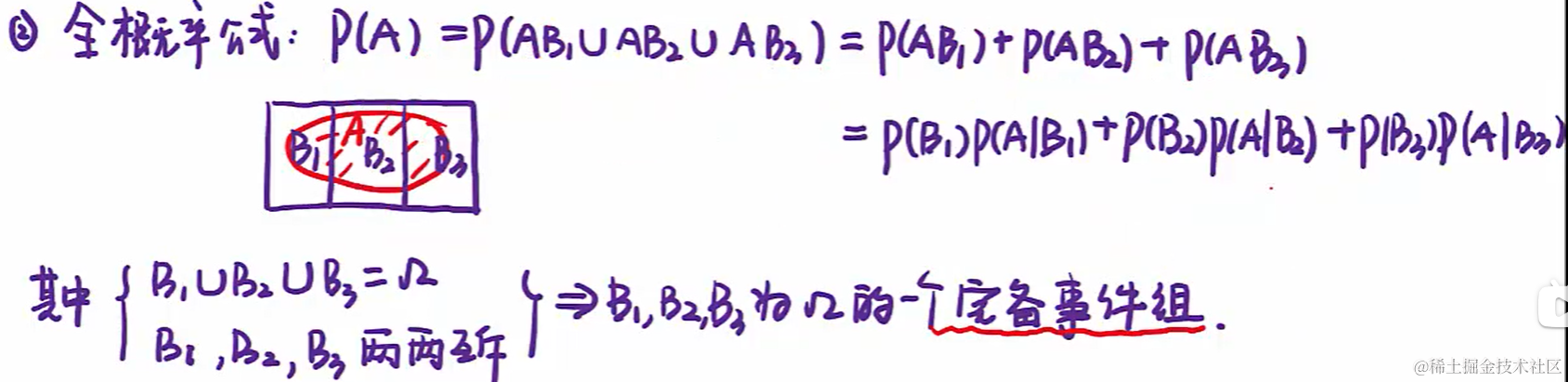

1.5 貝葉斯公式
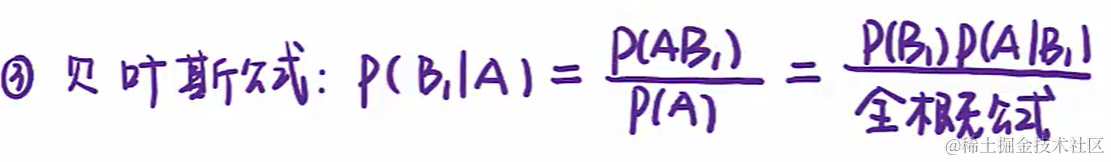

1.6事件概率(關系運算 / 條件概率)
加法:

減法:
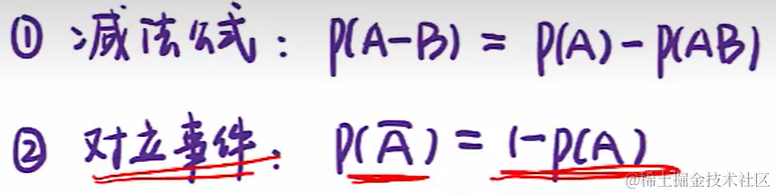
乘除:


相互獨立事件互不影響。
第二課
2.1 已知分布函數 Fx(x) 與密度函數 fx(x) 中的一項,求另一項
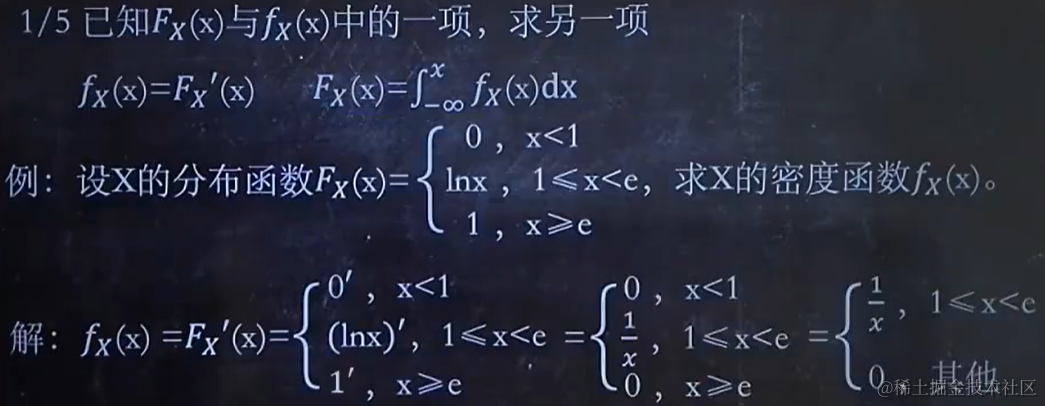
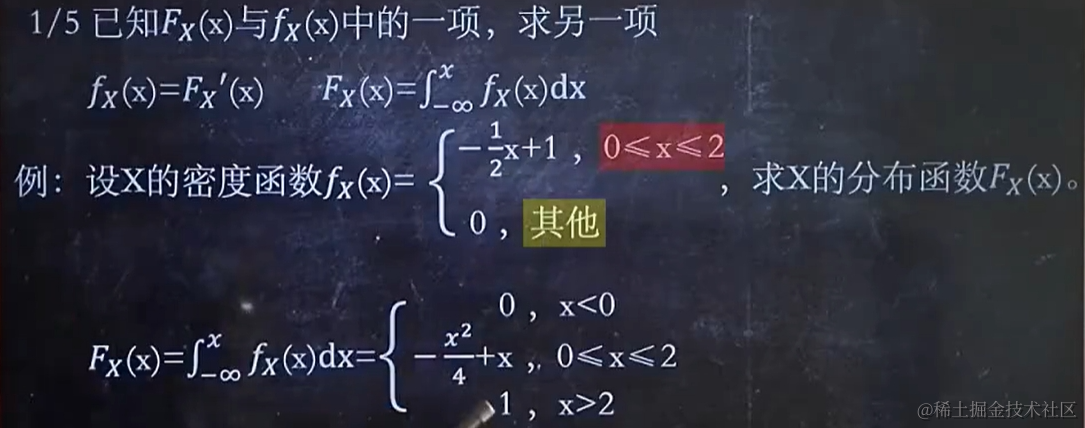
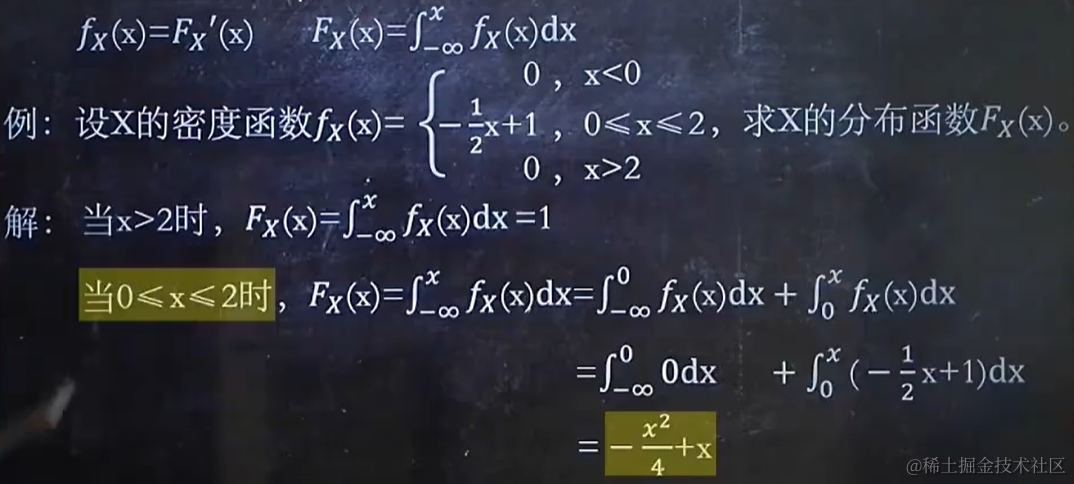
2.2 已知Fx(x)與fx(x)中的一種,求P
這里 P 里面的等于號不影響。F 或者 f 的x 下標有無對自身沒有影響。
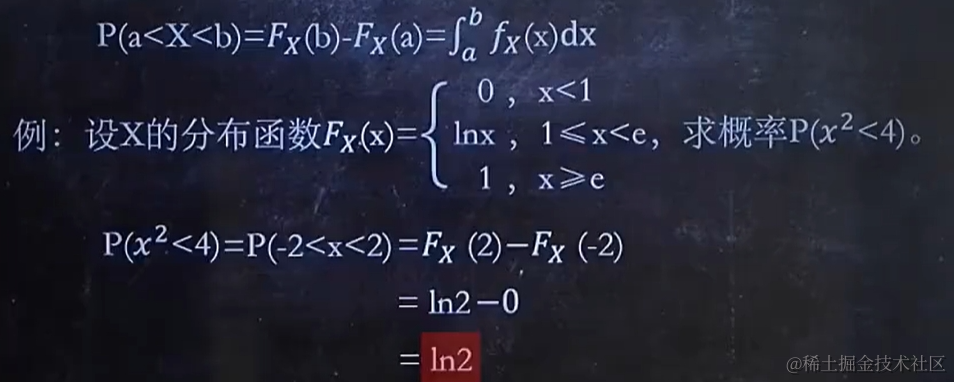
2.3 Fx(x)或fx(x)含未知數,求未知數
標準化的幾個公式。
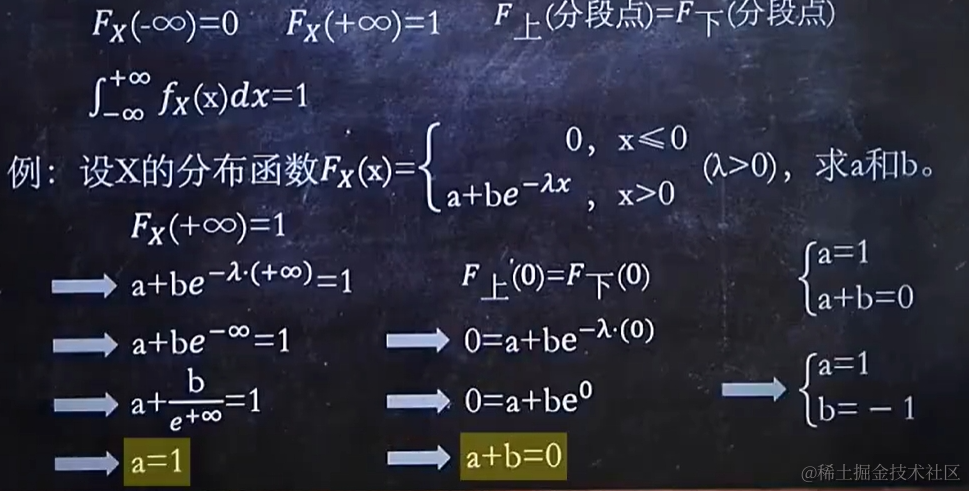
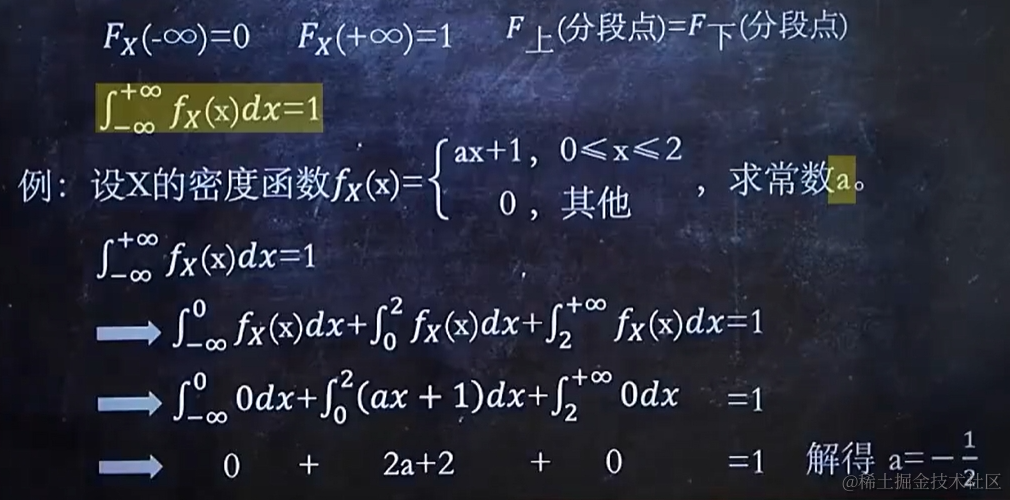
2.4 求分布律
分布列就是分布律。


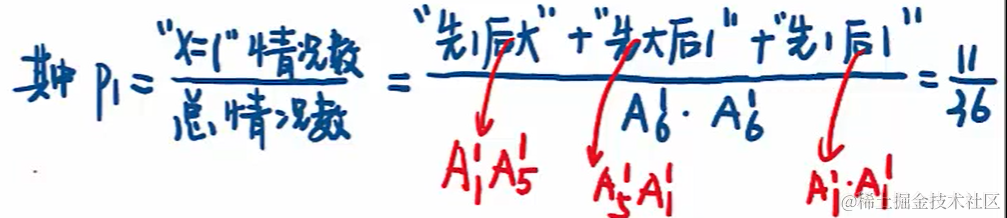
像擲骰子這樣的問題是順序問題(A)。
2.5 已知含有未知數分布列,求未知數
已知分布列如下,求 k 的值。

第三課
3.1 已知 X 分布列,求 Y 的分布列

以下寫法也可以:
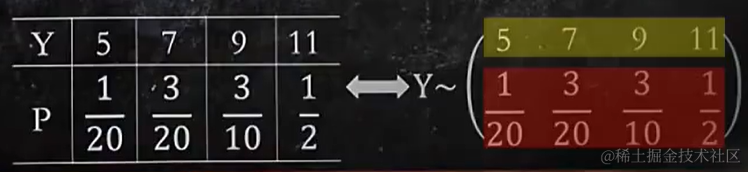
第四課
4.1 符合均勻分布,求概率
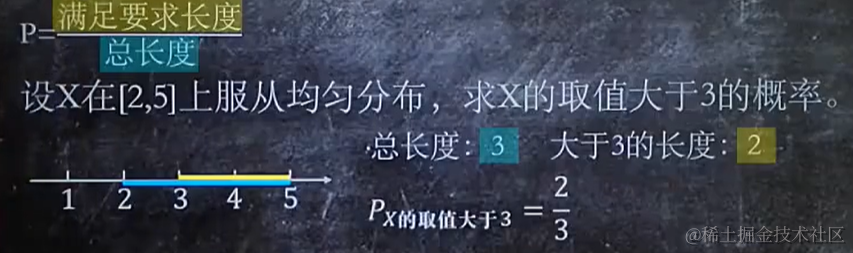

4.2 符合泊松分布,求概率

4.3 符合二項分布,求概率

4.4 符合指數分布,求概率

4.5 符合正態分布,求概率
標準正態分布,N(0, 1)。

第五課
5.1 已知二維離散型分布律,求?

5.2 已知二維離散型分布律,判斷獨立性


5.3 已知 F(x, y),求 f(x, y)

5.4 連續型二維變量的分布函數 F(x) 和概率密度 f(x)
5.4.1 求概率密度 f(x) 和 概率
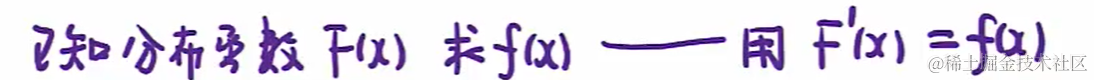

5.4.2 求待定系數和分布函數 F(x)


那如果有三個為未知項呢?利用分段點出連續可求。



第六課
6.1 求邊緣分布函數

6.2 求邊緣密度函數

6.3 判斷連續型二維變量的獨立性
fx(x) 和 fy(y) 在上一題型中已經求過。

6.4 二維離散型隨機分布(聯合、邊緣、條件分布和獨立性)


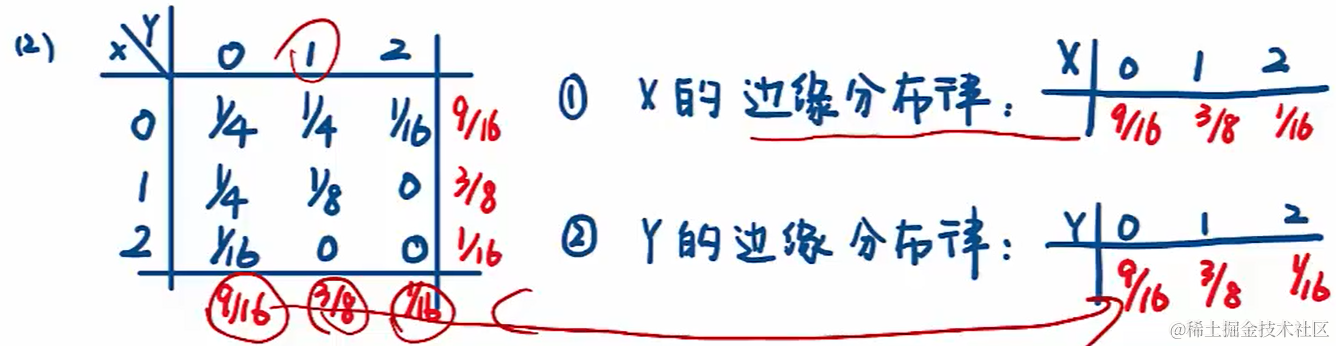
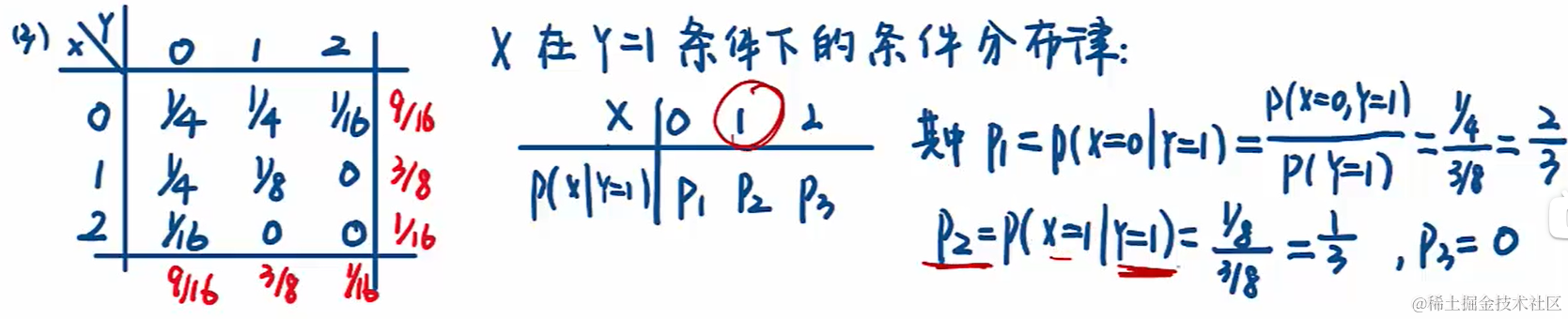

6.5 二維連續型隨機分布(聯合、邊緣、條件密度和獨立性)
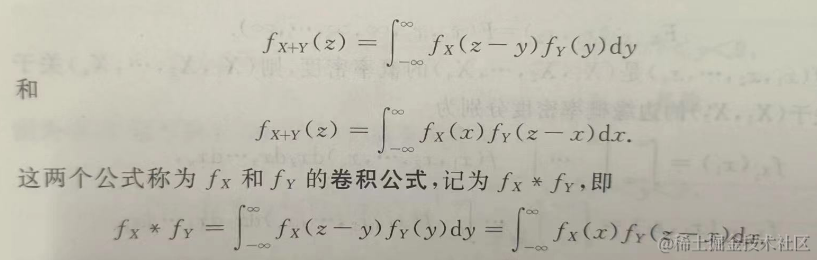

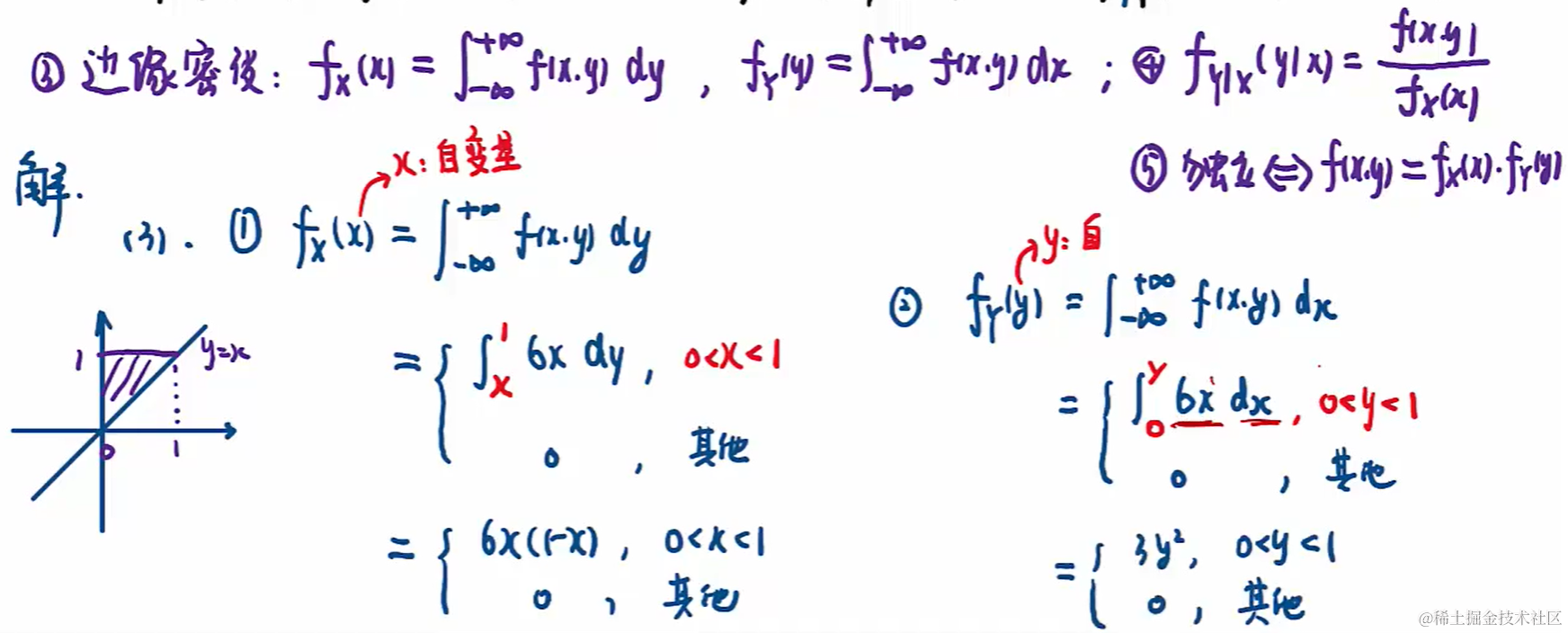
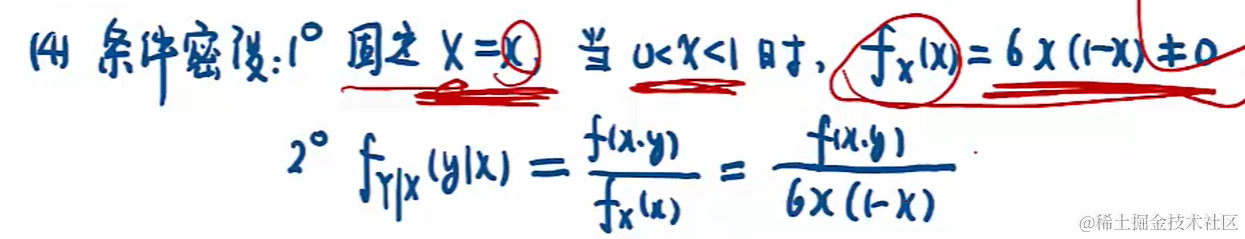


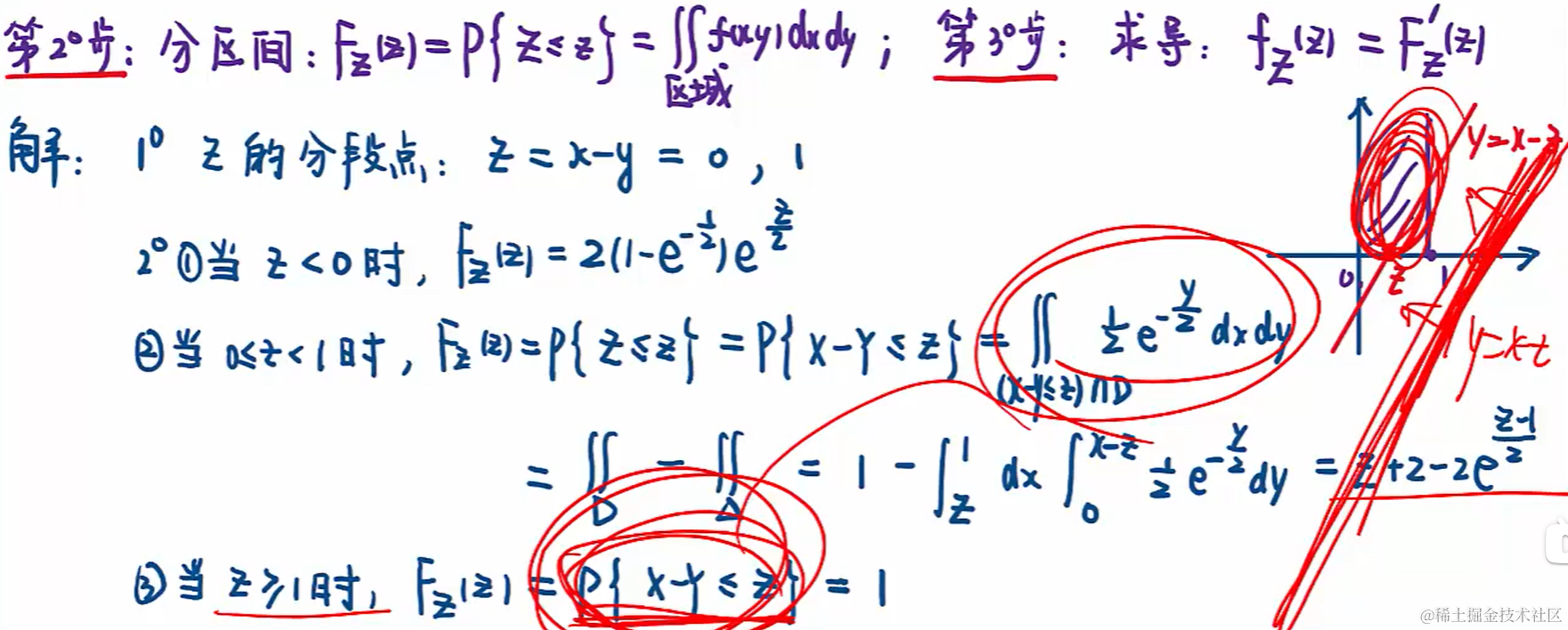
由規范性,矩形區域的概率就是 1。
離散型就是求分布律。
第七課
7.1 求離散型的期望 E(x)

7.2 求連續型的期望 E(x)

7.3 已知 Y= g(x), 求 E(y)


7.4 求方差 D(x)
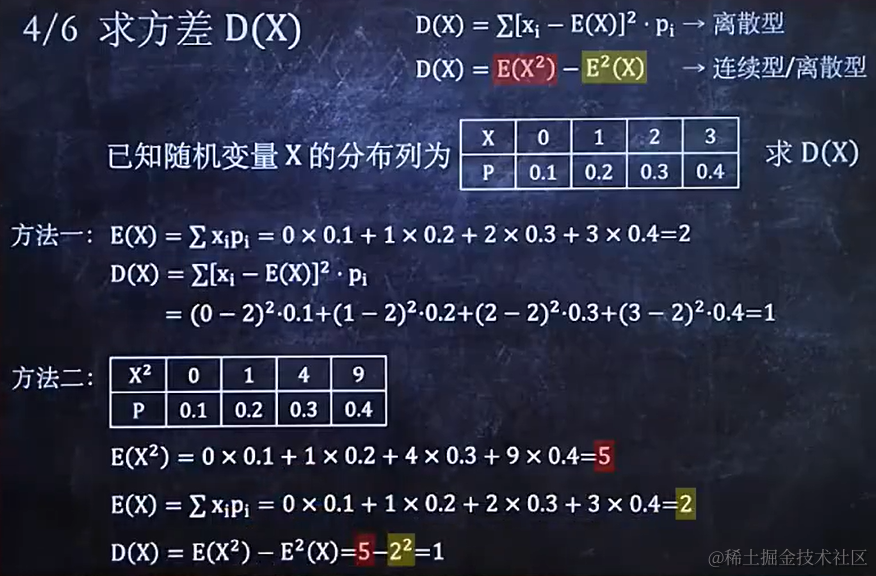
7.5 根據E(x)、D(x)的性質進行復雜運算

7.6 E(X)、D(X)與各種分布的綜合題

第八課
8.1 協方差 Cov、密度系數 Pxy、方差 D 相關類題目
離散型:

連續型:

P(rou) 不等于 0 ,則 X 和 Y 相關。
8.2 利用切比雪夫不等式求概率

8.3 多項獨立同分布,求總和怎樣的概率

第九課
9.1 求離散型的期望

9.2 求連續型的期望

9.3 已知Y=g(x),求E(Y)


9.4 求方差 D(x)
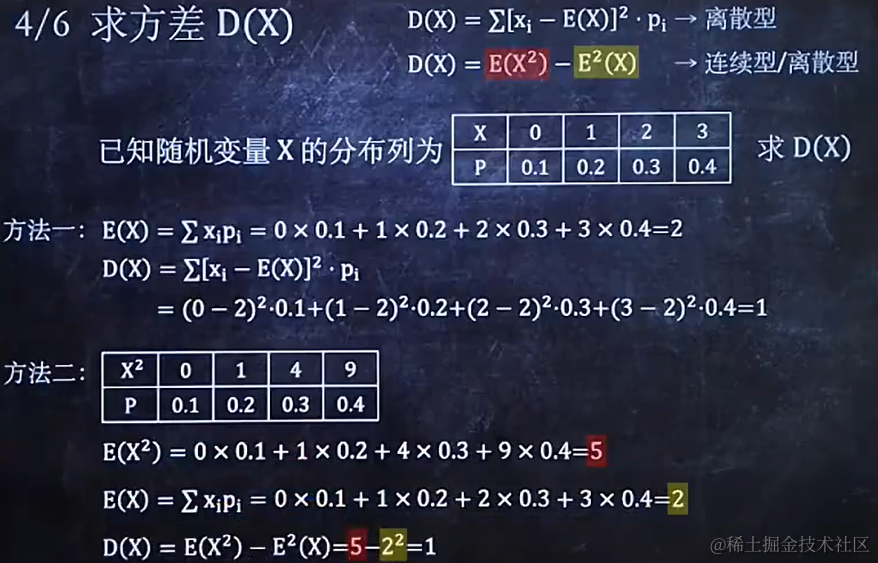
9.5 根據E(x)、D(x)的性質進行復雜運算

9.6 E(x)、D(x) 與各種分布的綜合題
0-1 分布:E(x) = p; D(x) = p(1 - p)

二項分布也是伯努利概型(獨立、n次重復試驗、每次只有 A 和 非A 兩種結果)。
第十課
中心極限定理
n個變量、獨立、同分布

規范化后得到標準正態:

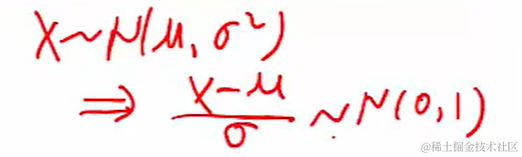



)

進行編譯)














