紅黑樹模擬實現

目錄

概念

性質

節點定義

紅黑樹的插入

完整代碼

概念

紅黑樹，是一種二叉搜索樹，但在每個結點上增加一個存儲位表示結點的顏色，可以是Red或Black。通過對任何一條從根到葉子的路徑上各個結點著色方式的限制，紅黑樹確保沒有一條路徑會比其他路徑長出倆倍，因而是接近平衡的。

下面就是一個紅黑樹：?

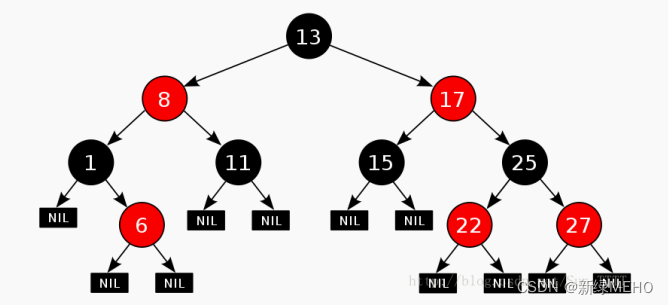
注：從根節點到NIL節點才是才算是一條路徑。

性質

1.每個結點不是紅色就是黑色

2.根節點是黑色的
3.如果一個節點是紅色的，則它的兩個孩子結點是黑色的
4.對于每個結點，從該結點到其所有后代葉結點的簡單路徑上，均包含相同數目的黑色結點5.每個葉子結點都是黑色的(此處的葉子結點指的是空結點)

節點定義
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};

?通過上面的代碼不難發現，我們將新創建的節點設置為紅色，為什么不設置成黑色呢？

根據紅黑樹的性質4，我們知道，每條路徑上黑色節點的數目是相等的，倘若我們在插入節點時，插入的是黑色節點，那么將影響整棵樹；插入的是紅色節點，不至于影響整棵樹，因為如果新插入節點的父節點是黑色，將不需要進行調整；如果新插入節點的父節點是紅色，只需要進行相關調整即可。

總的來說，新插入節點是紅色，影響范圍更小，利于編碼實現，更方便。

紅黑樹的插入

1.按照二叉搜索樹的規則插入節點；

2.判斷紅黑樹的結構是否被破壞。

因為新節點的默認顏色是紅色，因此：如果其父節點是黑色，就沒有違反紅黑樹任何行者，則不需要調整；但當新插入節點的父節點是紅色時，就違反了性質三（不能出現連續的紅色節點），此時需要對紅黑樹分情況來討論：

【約定】：cur為當前節點，p為父節點，g為祖父節點，u為叔叔節點。

情況一：cur為紅，p為紅，g為黑，u存在且為紅

解決方式：將p，u改為黑，g改為紅，然后把g改為cur，繼續向上調整。

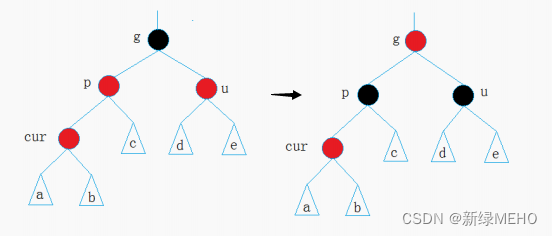
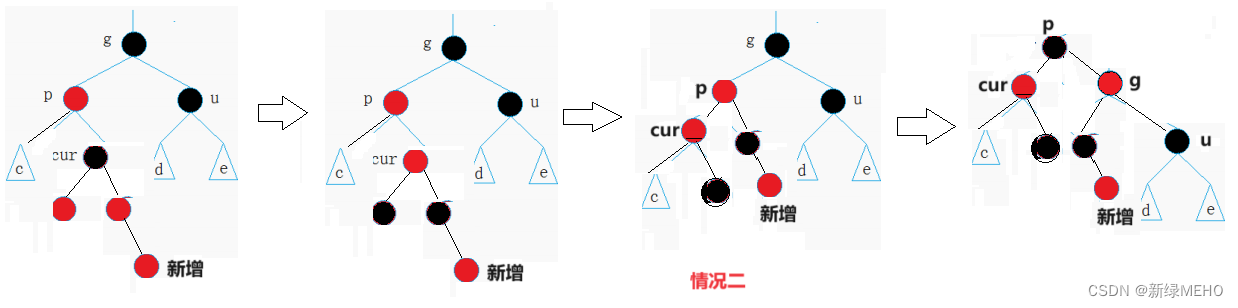
情況二：cur為紅，p為紅，g為黑，u不存在 / u存在且為黑

解決方式：p為g的左孩子，cur為p的左孩子，則進行右單旋，p改為黑色，g改為紅色；

? ? ? ? ? ? ? ? ? p為g的右孩子，cur為p的右孩子，則進行左單旋，p改為黑色，g改為紅色。

此時u有兩種情況：

1.u節點不存在，此時cur一定是新增節點，因為如果cur不是新插入節點，則cur和p一定有一個節點的顏色是黑色的，就不滿足性質四（每條路徑黑色節點個數相同）。

2.u節點存在，則其一定是黑色的.

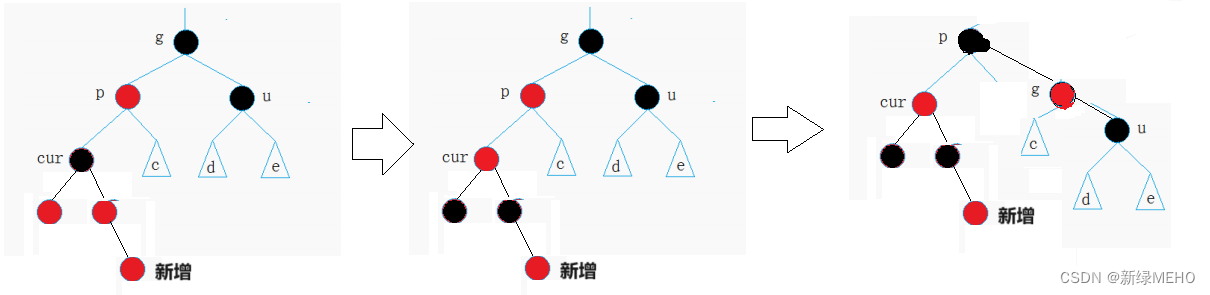
情況三：cur為紅，p為紅，g為黑，u不存在 / u存在且為黑

解決方式：p為g的左孩子，cur為p的右孩子，則進行左單旋，再右單旋,? p改為黑色，g改為紅色；

? ? ? ? ? ? ? ? ? p為g的右孩子，cur為p的左孩子，則進行右單旋，再左單旋,? p改為黑色，g改為紅色。

此時u有兩種情況：

1.u節點不存在，此時cur一定是新增節點，因為如果cur不是新插入節點，則cur和p一定有一個節點的顏色是黑色的，就不滿足性質四（每條路徑黑色節點個數相同）。

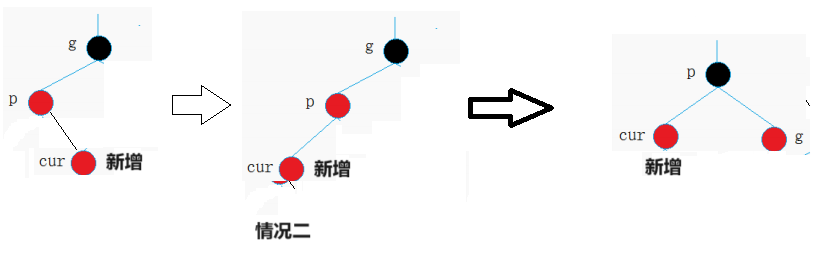
2.u節點存在，則其一定是黑色的.

插入代碼實現?

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新增節點給紅色cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){//     g//   p   u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上更新處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 單旋//     g//   p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 雙旋//     g//   p//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else  // parent == grandfather->_right{//     g//   u   p //          c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   u   p //     c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;
}
完整代碼
#pragma onceenum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新增節點給紅色cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){//     g//   p   u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上更新處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 單旋//     g//   p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 雙旋//     g//   p//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else  // parent == grandfather->_right{//     g//   u   p //          c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   u   p //     c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}// 根節點->當前節點這條路徑的黑色節點的數量bool Check(Node* root, int blacknum, const int refVal){if (root == nullptr){//cout << balcknum << endl;if (blacknum != refVal){cout << "存在黑色節點數量不相等的路徑" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "有連續的紅色節點" << endl;return false;}if (root->_col == BLACK){++blacknum;}return Check(root->_left, blacknum, refVal)&& Check(root->_right, blacknum, refVal);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;//參考值int refVal = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refVal;}cur = cur->_left;}int blacknum = 0;return Check(_root, blacknum, refVal);}private:Node* _root = nullptr;
};

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/41759.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/41759.shtml
英文地址，請注明出處：http://en.pswp.cn/web/41759.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

充電樁開源平臺，開發流程有圖有工具

充電樁開源平臺，開發流程有圖有工具

慧哥充電樁開源平臺產品研發流程是確保產品從概念階段到市場推廣階段的有序進行的關鍵。以下是對您給出的步驟的詳細解釋和建議&#xff1a; 設計業務流程: 在這一步&#xff0c;團隊需要確定產品的核心功能、目標用戶以及如何滿足用戶需求。進行市場調研&#xff0c;了解競爭…
閱讀更多...
PostMan Error:Maximum response size reached

PostMan Error:Maximum response size reached

一、問題描述 用postman本地測試&#xff0c;restful api接口導出文件&#xff0c;文件大小為190M&#xff0c;服務沒問題&#xff0c;總是在導出時&#xff0c;拋出&#xff1a;Error:Maximum response size reached。開始以為是服務相應文件過大或者相應時間超時導致的。其實…
閱讀更多...
ts和js的關系

ts和js的關系

https://www.typescriptlang.org/zh/docs/handbook/typescript-from-scratch.html TypeScript&#xff08;TS&#xff09;和 JavaScript&#xff08;JS&#xff09;都是用于開發前端和后端應用的編程語言&#xff0c;但它們有一些顯著的區別。以下是主要的區別&#xff1a; 1…
閱讀更多...
雙向鏈表 -- 詳細理解和實現

雙向鏈表 -- 詳細理解和實現

歡迎光顧我的homepage 前言 雙向鏈表是一種帶頭雙向循環的鏈表。在雙向鏈表中&#xff0c;首先存在著一個頭結點&#xff1b;其次每個節點有指向下一個節點的指針next 和指向上一個節點的指針prev &#xff1b…
閱讀更多...
Trimble realworks 2024.02 中文激活版獲取License下載軟件

Trimble realworks 2024.02 中文激活版獲取License下載軟件

Trimble realworks 2024 是領先的3D點云和2D圖像處理解決方案&#xff0c;使用可您提供了一組用于處理的工具&#xff0c;以便為您的應用程序&#xff08;或項目&#xff09;獲取必要的信息。此處理可以分為三種模式&#xff0c;在注冊中&#xff0c;您可以注冊相對于其他掃描和…
閱讀更多...
通信協議_Modbus協議簡介

通信協議_Modbus協議簡介

概念介紹 Modbus協議&#xff1a;一種串行通信協議&#xff0c;是Modicon公司&#xff08;現在的施耐德電氣Schneider Electric&#xff09;于1979年為使用可編程邏輯控制器&#xff08;PLC&#xff09;通信而發表。Modbus已經成為工業領域通信協議的業界標準&#xff08;De f…
閱讀更多...
大舍傳媒：如何在海外新聞媒體發稿報道摩洛哥？

大舍傳媒：如何在海外新聞媒體發稿報道摩洛哥？

引言 作為媒體行業的專家&#xff0c;我將分享一些關于在海外新聞媒體發稿報道摩洛哥的干貨教程。本教程將帶您深入了解三個重要的新聞媒體平臺&#xff1a;Mediterranean News、Morocco News和North African News。 地中海Mediterranean News Mediterranean News是一個知名…
閱讀更多...
合合信息大模型“加速器”重磅上線

合合信息大模型“加速器”重磅上線

大模型技術的發展和應用&#xff0c;預示著更加智能化、個性化未來的到來。如果將大模型比喻為正在疾馳的科技列車&#xff0c;語料便是珍貴的“燃料”。本次世界人工智能大會期間&#xff0c;合合信息為大模型打造的“加速器”解決方案備受關注。 在大模型訓練的上游階段&…
閱讀更多...
【計算機畢業設計】021基于weixin小程序微信點餐

【計算機畢業設計】021基于weixin小程序微信點餐

&#x1f64a;作者簡介&#xff1a;擁有多年開發工作經驗&#xff0c;分享技術代碼幫助學生學習&#xff0c;獨立完成自己的項目或者畢業設計。 代碼可以私聊博主獲取。&#x1f339;贈送計算機畢業設計600個選題excel文件&#xff0c;幫助大學選題。贈送開題報告模板&#xff…
閱讀更多...
Python學習中使用循環（for, while）

Python學習中使用循環（for, while）

在Python編程語言中&#xff0c;循環是一個非常重要的概念&#xff0c;可以幫助我們在代碼中重復執行某些操作。Python支持兩種主要的循環結構&#xff1a;for 循環和 while 循環。 1. for 循環 for 循環用于遍歷一個序列&#xff08;如列表、元組、字符串&#xff09;或其他…
閱讀更多...
第11章：標準化和軟件知識產權

第11章：標準化和軟件知識產權

第11章&#xff1a;標準化和軟件知識產權 標準化 國際標準(International Standard)是指國際標準化組織(ISO)、國際電工 委員會(IEC)所制定的標準。 標準 是對重復性事物和概念所做的統一規定。 標準化的特征包括橫向綜合性、政策性和統一性 。 標準化是指在經濟、技術、科學…
閱讀更多...
JAVA學習-練習試用Java實現“分發糖果”

JAVA學習-練習試用Java實現“分發糖果”

問題&#xff1a; 老師想給孩子們分發糖果&#xff0c;有 N 個孩子站成了一條直線&#xff0c;老師會根據每個孩子的表現&#xff0c;預先給他們評分。 需要按照以下要求&#xff0c;幫助老師給這些孩子分發糖果&#xff1a; 每個孩子至少分配到 1 個糖果。 評分更高的孩子…
閱讀更多...
FastAPI：高性能異步API框架

FastAPI：高性能異步API框架

文章目錄 引言官網鏈接FastAPI 原理1. 基于 Starlette 和 Pydantic2. 路由與依賴注入3. 自動文檔 使用方法安裝 FastAPI創建一個簡單的API運行服務器 優缺點優點缺點 結論 引言 在快速發展的Web和移動應用時代&#xff0c;構建高效、可擴展的API成為了現代軟件開發的關鍵需求之…
閱讀更多...
Thingsboard 系列之通過 ESP8266+MQTT 模擬設備上報數據到平臺

Thingsboard 系列之通過 ESP8266+MQTT 模擬設備上報數據到平臺

前置工作 Thingsboard平臺ESP 8266 NodeMCU 開發板IDE&#xff1a; Arduino 或 VScode 均可 服務端具體對接流程 系統管理員賬號通過 Thingsboard 控制面板創建租戶等信息并以租戶賬號登錄 實體 —> 設備維護具體設備信息 創建完成后通過管理憑據修改或直接復制訪問令牌…
閱讀更多...
python 冷知識 66 個 0708

python 冷知識 66 個 0708

66個有趣的Python冷知識 內聯注釋 可以在代碼行尾使用 # 進行內聯注釋&#xff0c;例如 x 10 # 這是一個內聯注釋。 多行注釋 多行注釋可以用三個引號 或 """ 包裹。 分數 fractions 模塊提供了分數類型&#xff0c;可以精確表示分數值。 小數 decimal 模塊…
閱讀更多...
致遠OA同步組織架構到企業微信

致遠OA同步組織架構到企業微信

致遠OA同步組織架構到企業微信 可適配任何系統 背景 原有的微協同無法滿足人員同步&#xff0c;因為在啟用微協同的時候&#xff0c;企業微信已經存在人員&#xff0c;所以配置微協同之后&#xff0c;人員會出現新增而不會同步修改 方案 重寫同步&#xff0c;針對已經存在…
閱讀更多...
Visual Studio下安裝引入Boost庫

Visual Studio下安裝引入Boost庫

背景&#xff1a; 在 Win 上通過 Visual Studio 運行 c 代碼&#xff0c;引入頭文件 #include <boost/...>&#xff0c;顯式無法打開&#xff0c;需要手動下載boost并進行配置。 1、下載boost&#xff1a; Boost官網&#xff1a;Boost Downloads 下載boost&#xff0c…
閱讀更多...
網安加·百家講壇 | 關昕健：新時代企業數據安全運營思路

網安加·百家講壇 | 關昕健：新時代企業數據安全運營思路

作者簡介&#xff1a;關昕健&#xff0c;某運營商安全專家&#xff0c;2015年獲CISSP認證&#xff0c;長期負責企業安全運營工作&#xff0c;關注國內外數據安全動態與解決方案&#xff0c;持續開展數據安全運營實踐。 近年來&#xff0c;隨著《數據安全法》的出臺和國家數據局…
閱讀更多...
Pytorch中的DataLoader類

Pytorch中的DataLoader類

&#x1f4da;博客主頁&#xff1a;knighthood2001 ?公眾號&#xff1a;認知up吧 &#xff08;目前正在帶領大家一起提升認知&#xff0c;感興趣可以來圍觀一下&#xff09; &#x1f383;知識星球&#xff1a;【認知up吧|成長|副業】介紹 ??如遇文章付費&#xff0c;可先看…
閱讀更多...
js逆向案例 | 加速樂反爬逆向

js逆向案例 | 加速樂反爬逆向

前言 加速樂作為一種常見的反爬蟲技術&#xff0c;在網絡上已有大量詳盡深入的教程可供參考。然而&#xff0c;對于那些初次接觸的人來說&#xff0c;直接面對它可能仍會感到困惑。 聲明 本文僅用于學習交流&#xff0c;學習探討逆向知識&#xff0c;歡迎私信共享學習心得。如…
閱讀更多...
最新文章

Copyright @ 2022~2023