排序（堆排序、快速排序、歸并排序)--＞深度剖析(二)

前言

前面介紹了冒泡排序、選擇排序、插入排序、希爾排序，作為排序中經常用到了算法，還有堆排序、快速排序、歸并排序

堆排序（HeaSort）

堆排序的概念

堆排序是一種有效的排序算法，它利用了完全二叉樹的特性。在C語言中，堆排序通常通過構建一個最大堆（或最小堆），然后逐步調整堆結構，最終實現排序。

代碼實現

堆排序是一種基于二叉堆的排序算法，它通過將待排序的元素構建成一個二叉堆，然后逐步移除堆頂元素并將其放置在數組的尾部，同時維護堆的性質，直至所有元素都被排序。

注意：第一個for循環中的（n-1-1）/ 2 的含義

第一個減1是由n-1個元素
第二個減1是除以2是父親節點。以為我們調整的是每一個根節點。（非葉子節點）

//堆排序
void HeapSort(int* a, int n)
{//建堆for(int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a,n,i);}//排序int end = n - 1;while(end > 0){Swap(&a[end], &a[0]);AdjustDown(a, end, 0);--end;}	
}

其中AdjustDown是建立堆的函數，我們要建立一個大堆，將替換到上上面的小值，向下調整，保持大堆的結構。

代碼如下：

//向下調整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}}

堆排序的復雜度分析

堆排序是一種常用的排序算法，其時間復雜度通常為O(nlogn)。在C語言中實現堆排序時，時間復雜度的分析主要涉及到兩個階段：構建初始堆和進行堆排序。

構建初始堆：從最后一個非葉子節點開始，逐步向上調整，直到根節點滿足堆的性質。這個過程的時間復雜度為O(n)，因為需要對每個非葉子節點進行一次調整。
進行堆排序：堆排序的過程涉及到多次交換堆頂元素和最后一個元素，并對剩余的元素進行調整。每次交換后，堆的大小減一，并對新的堆頂元素進行調整。這個過程的時間復雜度為O(nlogn)，因為每次調整的時間復雜度為O(logn)，總共需要進行n-1次調整。

快速排序(Quick Sort)

快速排序的概念

快速排序（Quick Sort）是一種高效的排序算法，它的基本思想是通過一趟排序將待排記錄分隔成獨立的兩部分，其中一部分記錄的關鍵字均比另一部分記錄的關鍵字小，然后再分別對這兩部分記錄繼續進行排序，以達到整個序列有序的目的。在C語言中，快速排序的實現通常涉及到遞歸函數的編寫，以及對數組進行分區（partition）操作。

霍爾版本（hoare）

在這里插入圖片描述

在這里我們是要，定義一個關鍵字（keyi）進行分區，然后分別向左右進行遞歸。

代碼實現

int part1(int* a, int left, int right)
{int mid = GetmidNum(a,left,right);Swap(&a[left], &a[mid]);int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi])right--;while (left < right && a[left] <=a[keyi])left++;Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;return keyi;
}

挖坑法

挖坑法類似于霍爾方法，挖坑就是記住關鍵字，保證關鍵字就是一個坑位，比關鍵字值小（大）的時候就入坑位，此時，這個值位置作為新的坑位直至兩個前后指針指向同一個坑位。

在這里插入圖片描述

代碼實現

int part2(int* a, int left, int right)
{int mid = GetmidNum(a, left, right);Swap(&a[left], &a[mid]);int keyi = a[left];int hole = left;while (left < right){while (left < right && a[right] >= keyi)right--;Swap(&a[hole], &a[right]);hole = right;while (left < right && a[left] <= keyi)left++;Swap(&a[hole], &a[left]);hole = left;}Swap(&keyi, &a[hole]);keyi = left;return keyi; }

前后指針法

prev 指針初始化為數組的開始位置，cur 指針初始化為 prev 的下一位置。
cur 指針向前遍歷數組，尋找小于或等于基準值的元素，而 prev 指針則跟隨 cur 指針的移動，直到 cur 找到一個小于基準值的元素。
一旦找到這樣的元素，prev 和 cur 指針之間的元素都會被交換，然后 cur 指針繼續向前移動，直到找到下一個小于基準值的元素，或者到達數組的末尾。最后，基準值會被放置在 prev 指針當前的位置，完成一次排序

在這里插入圖片描述

代碼實現

int part3(int* a, int left, int right)
{int mid = GetmidNum(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;int cur = left + 1;int prev = left;while (cur <= right){while (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}

遞歸實現

以上都是遞歸方法，通過調用分區進行排序。

void QuickSort(int* a, int left, int right)
{if (left >= right)return;int key = part3(a, left, right);QuickSort(a, left, key - 1);QuickSort(a, key + 1, right);}

快速排序迭代實現（利用棧）參考：棧和隊列

基本步驟

初始化棧：創建一個空棧，用于存儲待排序子數組的起始和結束索引。
壓棧：將整個數組的起始和結束索引作為一對入棧。
循環處理，在棧非空時，重復以下步驟：
- 彈出一對索引（即棧頂元素）來指定當前要處理的子數組。
- 選擇子數組的一個元素作為樞軸（pivot）進行分區。
- 進行分區操作，這會將子數組劃分為比樞軸小的左側部分和比樞軸大的

代碼實現

void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STpush(&st, left);STpush(&st, right);while (!STEmpty(&st)){int end = STTop(&st);STPop(&st);int begin = STTop(&st);STPop(&st);int keyi = part3(a, begin, end);if (keyi + 1 < end){STpush(&st, keyi + 1);STpush(&st, end);}if (begin < keyi - 1){STpush(&st, begin);STpush(&st, keyi - 1);}}STDestroy(&st);
}

快速排序的優化

優化角度從兩個方面切入

在選擇關鍵字的（基準值）時候，如果我們碰到了，有序數組，那么就會，減低排序效率。
- 方法一：三數取中，即區三個關鍵字先進行排序，將中間數作為關鍵字，一般取左端右端和中間值。
- 方法二：隨機值。利用隨機數生成。

三數取中代碼實現

int GetmidNum(int* a, int begin, int end)
{int mid = (begin + end) / 2;if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if(a[end]<a[begin]){return begin;}else{return end;}}else //a[begin]>a[mid]{if (a[begin] < a[end]){return begin;}else if (a[end] < a[mid]){return mid;}else{return end;}}

隨機選 key（下標）代碼實現

srand(time(0));
int randi = left + (rand() % (right - left));
Swap(&a[left], &a[randi]);

快速排序復雜度分析

在平均情況下，快速排序的時間復雜度為O(n log n)，這是因為每次劃分都能夠將數組分成大致相等的兩部分，從而實現高效排序。在最壞情況下，快速排序的時間復雜度為O(n^2)
除了遞歸調用的棧空間之外，不需要額外的存儲空間，因此空間復雜度是O(log n)。在最壞情況下，快速排序的時間復雜度可能是 O(n)，這是因為在最壞情況下，遞歸堆棧空間可能會增長到線性級別。

根據上述描述，優化快速排序是必要的。

歸并排序（Merge Sort）

在這里插入圖片描述

歸并排序的概念

歸并排序（Merge Sort）是一種基于分治策略的排序算法，它將待排序的序列分為兩個或以上的子序列，對這些子序列分別進行排序，然后再將它們合并為一個有序的序列。歸并排序的基本思想是將待排序的序列看作是一系列長度為1的有序序列，然后將相鄰的有序序列段兩兩歸并，形成長度為2的有序序列，以此類推，最終得到一個長度為n的有序序列。

基本操作：

分解：將序列每次折半劃分，遞歸實現，直到子序列的大小為1。
合并：將劃分后的序列段兩兩合并后排序。在每次合并過程中，都是對兩個有序的序列段進行合并，然后排序。這兩個有序序列段分別為 R[low, mid] 和 R[mid+1, high]。先將他們合并到一個局部的暫存數組 R2 中，合并完成后再將 R2 復制回 R 中。

代碼實現(遞歸)

void _MergeSort(int* a, int* tmp, int begin, int end)
{if (begin >= end)return;int mid = (begin + end) / 2;_MergeSort(a, tmp, begin, mid - 1);_MergeSort(a, tmp, mid + 1, end);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] > a[begin2]){tmp[i++] = a[begin2++];}else{tmp[i++] = a[begin1++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, tmp, 0, n-1);free(tmp);
}

代碼實現（迭代）

void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i =2* gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int j = i;if (end1 >= n || begin2 >= n){break;}if (end2 >= n){end2 = n-1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp); 
}

歸并排序復雜度分析

時間復雜度是 O(n log n)，其中 n 是待排序元素的數量。這個時間復雜度表明，歸并排序的執行速度隨著輸入大小的增加而線性增加，但不會超過對數級的增長。
空間復雜度為 O(n)，在數據拷貝的時候malloc一個等大的數組。

總結

p[j++] = a[begin2++];
}
}

		while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;
}
free(tmp);

}


## 歸并排序復雜度分析* 時間復雜度是 O(n log n)，其中 n 是待排序元素的數量。這個時間復雜度表明，歸并排序的執行速度隨著輸入大小的增加而線性增加，但不會超過對數級的增長。
* 空間復雜度為 O(n)，在數據拷貝的時候malloc一個等大的數組。# 總結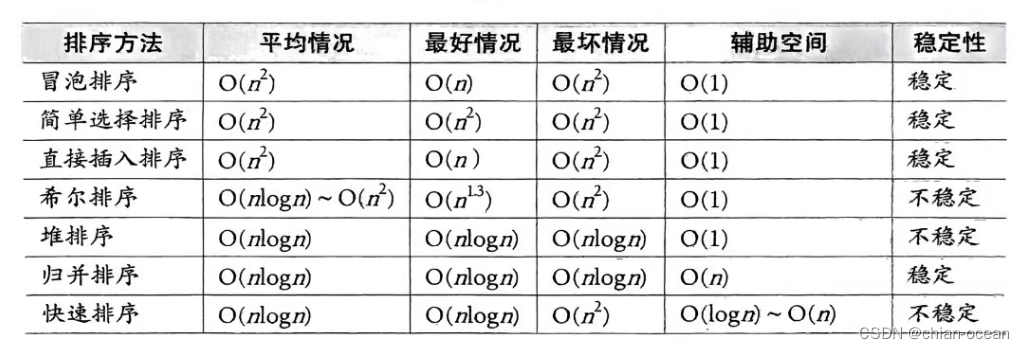![在這里插入圖片描述](https://img-blog.csdnimg.cn/direct/8d8d45e2fc8b4b0fa4747b27d20cd50c.png)