復分析——第9章——橢圓函數導論(E.M. Stein R. Shakarchi)

第 9 章橢圓函數導論

(An Introduction to Elliptic Functions)

The form that Jacobi had given to the theory of elliptic

functions was far from perfection; its flaws are obvious.

At the base we find three fundamental functions sn,

cn and dn. These functions do not have the same

periods...

In Weierstrass’ system, instead of three fundamental

functions, there is only one, ?(u), and it is the

simplest of all having the same periods. It has only

one double infinity; and finally its definition is so that

it does not change when one replaces one system of

periods by another equivalent system.

(?? Jacobi 給出的橢圓函數理論形式遠非完美，其缺陷顯而易見。在基礎部分，我們發現三個基本函數 sn、cn 和 dn。這些函數的周期并不相同……

??? 在 Weierstrass 的系統中，沒有三個基本函數，只有一個，?(u)，它是所有具有相同周期的函數中最簡單的一個。它只有一個雙無窮大；最后，它的定義是，當用另一個等價系統替換一個周期系統時，它不會改變。)

-------------------------------------------------------------------------------------------------H. Poincaré,1899

??? 橢圓函數理論最初源于對橢圓積分的研究，它在數學的多個領域都受到廣泛關注。通常，那些積分可以被描述為形如? $\int R(x,\sqrt{P(x)})dx$ ?和形式。其中 R 是比率函數(rational function)，P 是三次或四次多項式(注：P 為二次多項式的情況在本質上是“圓函數(circular functions)”，可以簡化為三角函數? $\sin{x}$ ?、 $\cos{x}$ ??等)。這些積分用于計算橢圓或雙紐線(lemniscate)的弧長，以及各種其他問題。它們的早期研究集中在其特殊的變換性質和固有雙周期性的發現上。我們在上一章第 4.5 節中討論的半平面到矩形的映射函數中看到了后一種現象的一個例子。

正是 Jacobi 通過系統地研究雙周期函數(稱為橢圓函數)改變了這一主題。在這個理論中，他引入的 θ 函數(theta functions)起著決定性的作用。在他之后，Weierstrass發展了另一種方法，這種方法在初始階段更簡單、更優雅。它基于他的 ? 函數(譯注：符號 ? 稱為 weierstrass p ，其 Unicode為 “02118” , LaTex語法為“\wp”)，在本章中，我們將概述該理論的發端。我們將通過考慮 Eisenstein 級數及其涉及除數函數的表達式，盡可能地瞥見與數論的可能聯系。θ 函數與組合學(combinatorics)和數論有許多更直接的聯系，我們將在下一章中討論。我們將在那里看到的顯著事實證明了這些函數在數學中具有極大的影響(interest)。因此，它們應該會弱化上面關于 Jacobi 理論不完善的嚴厲意見。

1.? 橢圓函數(Elliptic functions)

我們感興趣的是在 ? 上具有兩個周期的亞純函數 f ；即，存在兩個非零復數? $\omega_{1}$ ?和? $\omega_{2}$ ?使得?

$f ( z + \omega_{1}) = f(z)$ ?和? $f ( z + \omega_{2}) = f(z)$ ?(對于任意 z∈? )。

我們稱具有兩個周期的函數為雙周期函數(doubly periodic functions)。當 ? $\omega_{1}$ ?和? $\omega_{2}$ ?在 ? 上是線性相關(即 ? $\omega_{2}/\omega_{1} \in \mathbb{R}$ ?)?時的這種情況我們是不感興趣的。事實上，練習 1 表明，在這種情況下，f 要么是具有簡單周期的同期函數(若商?? $\omega_{2}/\omega_{1}$ ?是比率的),要么 f 是一個常量(若商? $\omega_{2}/\omega_{1}$ ?是非比率的)。因此，我們做以下假設： $\omega_{1}$ ?和? $\omega_{2}$ ?在 ? 上是線性無關的。

我們現在描述一種將在本章中廣泛使用的規范化方法(normalization)。令? $\tau=\omega_{2}/\omega_{1}$ ?。由于 𝝉 和 1/𝝉 具有相反符號的虛部，且因為 𝝉 不是實數，故我們可以假設(在可能的交換? $\omega_{1}$ ? 和? $\omega_{2}$ ?的角色之后)Im(𝝉) > 0 。現在注意到，對于函數 f ，當且僅當函數? $F(z)=f(\omega_{1}z)$ ?具有周期 1 和 𝝉 時，其才具有周期? $\omega_{1}$ ?和? $\omega_{2}$ ?

，此外，當且僅當 F 是亞純函數時，f 是亞純函數。再者，f 的屬性直接推導于 F 。因此，我們可以不失一般性地假設，f 是在 ? 上具有周期 1 和 𝝉 的亞純函數(其中，Im(𝝉) > 0 )。

??? 連續應用周期性條件可得出

(1)??? f (z + n + m 𝝉) = f?(z)? (對于任意整數 n ，m 和任意 z∈? )，

因此，很自然地考慮定義為

$\Lambda = \{ n + m\tau: n ,m \in \mathbb{Z} \}$ ?

的 ? 中的晶格(lattice，或稱格點)。

??? 我們稱 1 和 𝝉 生成(generate) Λ (見圖 1 )。

------------------------------------------圖1:?由 1 和 𝝉 生成格式 Λ -----------------------------------------------------

等式(1)指的是，f 在按 Λ 的元素的平移下是常量。與晶格 Λ 相關的是定義為

$P_{0} = \{ z\in \mathbb{C}: z = a + b\tau , 0 \le a < 1 \:\:\mathrm{and}\:\: 0 \le b < 1\}$ ? 。

的基礎平行四邊形(fundamental parallelogram)。

??? 基本平行四邊的重要性源于 f 完全確定于其在?? $P_{0}$ ??上的行為這個事實。為了理解這一點，我們需要一個定義：對于兩個復數 z 和 w ，若

??????? ??? $z = w + n + m\tau$ ? (對于某些 n ，m ∈? ),

則稱這兩個復數是模 Λ 同余的(congruent mudulo Λ)，我們記為 z ~ w 。換句話說，z 和 w 在晶格中相差一個點，即 z - w ∈Λ 。根據(1)我們推斷出,只要 z ~ w ，則 f (z) = f(w) 。若我們可以證明，z∈? 中的任意點與? $P_{0}$ ?中的一個唯一點是同余的，則我們將完成證明 f 完全由其在基本科行四邊形中的值確定。假設已知 z = x + iy ，并記為 z = a + bτ (其中，a ，b ∈? ))。這是合理的，因為 1 和 𝝉 構成了二維向量空間 ? 的實數(reals)之上的一個基底(basis)。然后，分別選擇 ≤ a 和 ≤ b 的最大整數 n 和 m 。若我們令 w = z - n – mτ ，則根據定義有 z ~ w ，此外，w = (a - n) + (b - m) 𝝉。根據構造，顯然? $w \in P_{0}$ ?。為了證明唯一性，假設? $w$ ?和? $w^{'}$ ?是? $P_{0}$ ?中的兩個同余的點。若我們記為 w = a + bτ 和? $w^{' }= a^{'} + b^{'}\tau$ ?，則? $w - w^{'}= (a - a^{'}) + (b - b^{'}) \tau \in \Lambda$ ?，因此? $(a - a^{'})$ ?和? $(b - b^{'})$ ?均為整數。但是由于? $0 \le a , a^{'} < 1$ ?, 我們有? $-1 < a - a^{'} < 1$ ??，則這意味著? ? $a - a^{'} = 0$ ?。類似地，? $b - b^{'} = 0$ ?，從而我們推導出? $w=w^{'}$ ?。

更一般地，一個周期平行四邊形 P 是基礎平行四邊形的任意平移，即? $P = P_{0} + h ( h \in \mathbb{C} )$ ?(見圖 2 ) 。

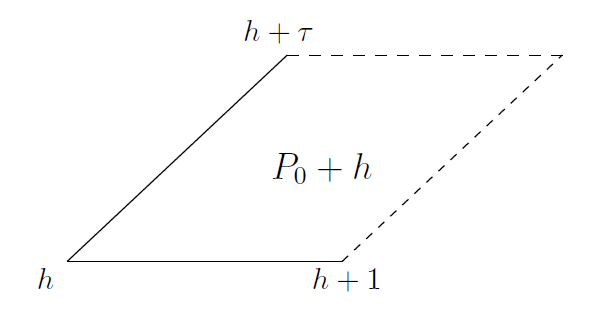
-----------------------------------------------------圖 2:?一個周期平行四邊形------------------------------------------

由于我們可以應用引理于 z - h ，我們推斷出 ? 中的每一個點都與已知周期平行四邊形中的唯一點同余。因此，f 由其在任何周期平行四邊形上的行為唯一決定。

??? 最后，注意到 $\Lambda$ ?和? $P_{0}$ ?導致(give rise to)復平面

$\mathbb{C} = \bigcup_{n,m \in \mathbb{Z} }(n + m\tau+P_{0})$ ?

的覆蓋(covering)(或平鋪(tiling))，此外，這個并集是不相交的。從我們剛剛收集的事實和? $P_{0}$ ??的定義可以立即得出這個結論。我們總結一下迄今為止所看到的內容。

命題 1.1 假設 f 是一個具有兩個生成晶格 Λ 的周期 1 和 𝝉 的亞純函數。則：

( i ) ? 中的每一個點都與基礎平行四邊行中的一個唯一點同余。

( ii ) ? 中的每一個點都與任意已知的周期平行四邊行中的一個唯一點同余。

( iii ) 晶格 Λ 在(2)的意義上提供了復平面的一個不相交的覆蓋。

( iv ) 函數 f 完全確定于其在任何周期平行四邊形中的值。

1.1? Liouville定理(Liouville’s theorems)

??? 現在我們可以明白為什么我們從一開始就假設 f 是亞純的而不是全純的。

定理 1.2 ?復可積的雙周期函數是常量。

證明：

函數完全由其在? $P_{0}$ ?上的值確定，因為 ? $P_{0}$ ? 的閉包是緊的，我們推斷出函數在 ? 上有界。因此，根據第 2 章中給出的 Liouville 定理，函數是常量。非常量雙周期亞純函數被稱為隨圓函數(elliptic function)。由于亞純函數在任何大圓盤上只能有有限多個零點和極點，因此我們看到橢圓函數在任何已知周期平行四邊形中也只能有有限多個零點和極點，尤其是在基礎平行四邊形中。當然，不能排除 f 在? $P_{0}$ ??的邊界上有一個極點或零點。

像往常一樣，我們用重數(multiplicity)計算極點和零點。記住這一點，我們可以證明以下定理。

定理 1.3 一個橢圓函數在? $P_{0}$ ?中的極點總數總是 ≥ 2 。

換句話說，f 不會只有一個簡單極點。它一定至少有兩個極點，并且這不能排除重數 ≥ 2 的單極點的情況。

證明：

??? 首先假設 f 在基礎平行四邊形在邊界? $\partial P_{0}$ ?上沒有極點。根據留數定理，我們有

$\displaystyle \int_{\partial P_{0}}f(z)dz = 2{\pi}i\sum{\mathrm{res}}\:{f}$ ?，

我們推斷出積分是 0 。為了理解這一點，我們簡單地應用 f 的周期性。注意到

$\displaystyle \int_{\partial_{P_{0}}}f(z)dz=\int_{0}^{1}f(z)dz+\int_{1}^{1+\tau}f(z)dz+\int_{1+\tau}^{\tau}f(z)dz+\int_{\tau}^{0}f(z)dz$ ?，

且對邊的積分相消。例如

$\begin{array}{rlc}\displaystyle \int_{0}^{1}f(z)dz+\int_{1+\tau}^{\tau}f(z)dz &\displaystyle = \int_{0}^{1}f(z)dz +\int_{1}^{0}f(s+\tau)ds \\ \\ &\displaystyle = \int_{0}^{1}f(z)dz +\int_{1}^{0}f(s)ds \\ \\ &\displaystyle = \int_{0}^{1}f(z)dz -\int_{0}^{1}f(z)dz \\ \\ &\displaystyle = 0 \end{array}$ ? 。

對于其它成對的邊也類似。因此， $\displaystyle \int_{\partial P_{0}} f = 0$ ?且? $\sum{\mathrm{res}}\:{f}=0$ ?。因此，f??在 $P_{0}$ ?中一定至少有兩個極點。

若 f 在?? $\partial P_{0}$ ?上有一個極點，選擇一個小的 h∈? 使得?? $P = h + P_{0}$ ???，則 f 在 ?P 上沒有極點。如前論證，我們求得 f 在 P 中一下至少有兩個極點，且因為同樣的結論對于 ? $P_{0}$ ?也成立。

橢圓函數的極點總數(按其重數計算)稱為其階(order)。下一個定理說，如果零點按其重數計算，則橢圓函數的零點數與極點數一樣多。

定理 1.4 ?每一個 m 階橢圓函數在 ? $P_{0}$ ?中都有 m 個零點。

證明：

??? 首先假設 f 在? $P_{0}$ ?和邊界上沒有零點或極點，我們知道，通過第 3 章中的幅角原理(argument principle)，有?

$\displaystyle \int_{?{\partial}P_{0}}\frac{f^{'}(z)}{f(z)}dz=2{\pi}i(\mathcal{N}_{\mathfrak{z}}-\mathcal{N}_{\mathfrak{p}})$ ?，

(譯注：符號 𝖟 是字母 z 的德文尖角體，符號 𝖕 是字母 p 的德文尖角體)

其中， $\mathcal{N}_{\mathfrak{z}}$ ?和? $\mathcal{N}_{\mathfrak{p}}$ ?分別表示? $P_{0}$ ?中 f 的零點和極點數。根據周期性，我們可以按前面定理的證明那樣論證，以求得? $\int_{\partial P_{0}}f^{'}/f=0$ ?，因此， $\mathcal{N}_{\mathfrak{z}}=\mathcal{N}_{\mathfrak{p}}$ ?。

在當 f 的零點或極點位于? $\partial P_{0}$ ?上的時候的這種情況下，只需將幅角原理應用到 P 的平移上即可。

??? 因此，若 f 是一個橢圓，則方程 f (z) = c 具有與 f 的階相同數量的解(對于每一個 c∈?)，只因為 f – c 是橢圓，并且具有與 f 同樣多的極點。

???????? 盡管上述定理相當簡單，但仍存在證明橢圓函數存在的問題。現在我們來談談這個問題的建設性解決方案。

1.2? Weierstrass ? 函數(The Weierstrass ? function)

1.2.1 ?2階橢圓函數(An elliptic function of order two)

??? 本節專門介紹橢圓函數的基本例子。如上所示，任何橢圓函數都一定至少有兩個極點；事實上，我們將構造一個橢圓函數，其唯一奇點將是周期生成的晶格上的雙極點。

??? 在研究雙周期函數的情況之前，讓我們首先簡要考慮只有一個周期的函數。如果想要構造一個周期為 1 且極點位于所有整數處的函數，一個簡單的選擇是求和?

$\displaystyle F(z)=\sum_{n=-\infty}^{\infty}\frac{1}{z+n}$ ?。

注意，若我們用 (z + 1) 替換 z ，這個和保持不變，且極點位于整數處。然而，定義 F的這個級數不是絕對收斂的。為了補救(remedy)這個問題，我們按對稱求和，即，我們定義

? $\displaystyle F(z)=\lim_{N \rightarrow \infty}\sum_{|n|\le N}\frac{1}{z+n}=\frac{1}{z}+\sum_{n=1}^{\infty}\left [ \frac{1}{z+n} + \frac{1}{z-n}\right ]$ ?。

在最右側，我們已經配對了(paired up)對應的 n 和 –n 項，這是一種技巧，使得方括號中的量? $O(1/n^{2})$ ?譯注：表示右側以? $1/n^{2}$ ?界)，因此，最后的和是絕對收斂的。因而，F 是亞純的且極點恰好位于整數處。事實上，我們在前面的第 5 章中已經證明? $F(z) = {\pi}\cot{?{\pi}}{z}$ ?。

存在第二種處理級數? $\sum_{n=-\infty}^{\infty}1/{(z+n)}$ ?的方式，將其記為

$\displaystyle \frac{1}{z}+\sum_{n \ne 0}^{}\left [ \frac{1}{z+n} - \frac{1}{n}\right ]$ ? ，

其中，求和是在所有非零整數上進行的。注意到，? $1/(z + n) - 1/n = O(1/n^{2})$ ?，這使得這個級數絕對收斂。此外，由于?

$\displaystyle \frac{1}{z+n} + \frac{1}{z-n}=\left (\frac{1}{z+n} - \frac{1}{n} \right )+\left (\frac{1}{z-n}-\frac{1}{-n} \right )$ ?，

我們得到與使用前面的方法而得到和相同。

??? 與此類似，我們的想法是模仿(mimic)上面的內容來產生我們的第一個橢圓函數的例子。我們想將其寫成

$\displaystyle \sum_{\omega \in \lambda}\frac{1}{(z+\omega)^{2}}$ ?，

但這個級數同樣不是絕對收斂的。有幾種方法可以嘗試理解這個級數(參見問題 1 )，但最簡單的方法是遵循我們處理余切級數的第二種方法。

??? 為了克服這個級數的非絕對收斂性，我們令? $\Lambda^{*}$ ?表示晶格減去原點，即? ? $\Lambda^{*}=\Lambda - \{(0,0)\}$ ?，我們轉而考慮以下級數：

$\displaystyle \frac{1}{z^{2}}+\sum_{\omega \in \Lambda^{*}}\left [\frac{1}{(z+\omega)^{2}}-\frac{1}{\omega^{2}} \right ]$ ?，

其中，我們已經減去了因子? $1/\omega^{2}$ ?以使得和式收斂。現在，方括號中的項是

$\displaystyle \frac{1}{(z+\omega)^{2}}-\frac{1}{\omega^{2}}=\frac{-z^{2}-2z\omega}{(z+\omega)^{2}\omega^{2}}=O(\frac{1}{\omega^{3}})$ ?(當 |ω|? ∞ 時)，

一旦我們證明了以下引理，新的級數將定義一個具有所需極點的亞純函數。

引理 1.5 兩個級數

$\displaystyle \sum_{(n,m)\ne (0,0)}\frac{1}{(|n|+|m|)^{r}}$ ? 和?? $\displaystyle \sum_{n+m\tau \in \Lambda^{*}}\frac{1}{|n+m\tau|^{r}}$ ?(若 r > 2)

收斂。

??? 回顧一下，根據第 7 章末尾的評注，二重級數是否絕對收斂的問題與求和的順序無關。在本例中，我們首先對 m 求和，然后對 n 求和。

對于第一個級數，可以應用通常的積分比較(注：當 k – 1 ≤ x ≤ k 時，我們簡單地使用? $1/k^{r} \le 1/x^{r}$ ?；此外，可參見第 I 冊第 8 章中的第一個圖)。對于每一個 n? ≠ 0 ,有

$\begin{array}{rlc} \displaystyle \sum_{m\in \mathbb{Z}}\frac{1}{(|n|+|m|)^{r}}=&\displaystyle \frac{1}{|n|^{r}}+2\sum_{m \ge 1}\frac{1}{(|n|+|m|)^{r}} \\ \\ =&\displaystyle \frac{1}{|n|^{r}}+2\sum_{k \ge |n|+1}\frac{1}{k^{r}} \\ \\ \le &\displaystyle \frac{1}{|n|^{r}}+2\int_{|n|}^{\infty}\frac{dx}{x^{r}} \\ \\ \le &\displaystyle \frac{1}{|n|^{r}}+C\frac{1}{|n|^{r-1}} \\ \\ \end{array}$ ?。

因此，r > 2 意味著

$\begin{array}{rlc} \displaystyle \sum_{(n,m)\ne (0,0)}\frac{1}{(|n|+|m|)^{r}} =&\displaystyle \sum_{|m| \ne 0}\frac{1}{|m|^{r}}+\sum_{|n|\ne 0}\sum_{m\in \mathbb{Z}}\frac{1}{(|n|+|m|)^{r}} \\ \\ \le &\displaystyle \sum_{|m| \ne 0}\frac{1}{|m|^{r}} +\sum_{|n|\ne 0} \left (\frac{1}{|n|^r}+C\frac{1}{|n|^{r-1}} \right ) \\ \\ < &\infty \end{array}$ ?。

為了證明第二個級數也是收斂的，只需證明存在一個常量 c 使得

??????????? |n| + |m| ≤ c| n + 𝒯m | (對于任意 n，m∈?)

即可。若存在一個正常量 a 使得 x ≤ ay，則我們記為 x ? y (譯注：符號的 Unicode 碼是“02272”，LaTex語法是“\lesssim”,讀作“小于相似”)。此外，若 x ? y 和 y ? x 均成立，我們記為 x ≈ y 。注意到，對于任意兩個正常量 A 和 B ，我們有

$(A^{2}+B^{2})^{1/2}\approx A+B$ ? 。

在一方面，?? $A \le (A^{2}+B^{2})^{1/2}$ ?且? $B \le (A^{2}+B^{2})^{1/2}$ ?，因此? $A+B \le 2(A^{2}+B^{2})^{1/2}$ ?。在另一方面，只需對兩側進行平方便可得到

$(A^{2}+B^{2})^{1/2} \le A + B$ ? 。

現在，引理 1.5 中第二個級數收斂的證明是通過以下觀察而得出的結果：

??????????? |n| + |m| ≈ | n + m𝒯 |? ( 只要 𝒯∈?) 。

事實上，若 𝒯 = s + it (s , t∈? 且 t > 0)，則根據前面的觀察，我們有

$| n + m\tau| = [(n+ms)^{2}+(mt)^{2}]^{1/2} \approx |n + ms| + |mt| \approx |n + ms| + |m|$ ?。

從而，通過分別考慮|n| ≤ 2|ms|和 |n| ≥ 2|ms|這兩種情況，我們得到 |n + ms| + |m| ≈ |n| + |m|。

評注：

上述證明表明，當 r > 2 時， $\sum(n + m\tau)^{-r}$ ?在每一個半平面 Im(𝒯)≥ δ > 0 中一致收斂。對比而方，當 r = 2 時，這個級數不收斂(練習 3 )。有了這個技術點，我們現在可以回到 Weierstrass ? 函數的定義，其由級數

$\begin{array}{rlc} \displaystyle {\wp}(z)=&\displaystyle \frac{1}{z^{2}}+\sum_{\omega \in \Lambda^{*}}\left [\frac{1}{(z+\omega)^{2}}-\frac{1}{\omega^{2}} \right ] \\ \\ =&\displaystyle \frac{1}{z^{2}}+\sum_{(n,m)\ne (0,0)}\left [\frac{1}{(z+n+m\tau)^{2}}-\frac{1}{(n+m\tau)^{2}} \right ] \end{array}$ ?。（譯注：符號“? ”是Weierstrass p 。）

我們斷言，? 是一個在晶格上具有雙極點的亞純函數。為了理解這一點，假設 |z| < R ，并寫成

$\displaystyle {\wp}=\frac{1}{z^{2}}+\sum_{|\omega| \le 2R}\left [\frac{1}{(z+\omega)^{2}}-\frac{1}{\omega^{2}} \right ] +\sum_{|\omega| > 2R}\left [\frac{1}{(z+\omega)^{2}}-\frac{1}{\omega^{2}} \right ]$ ? 。

第二項和中的項對于|z| < R 是一致地? $O(1/\omega^{3})$ ?的，因此，根據引理 1.5 這第二項和在域 |z| < R 內定義了一個全純函數。最后，請注意第一項和在圓盤 |z| < R ?中的格點(lattice points)上呈現雙極點。

注意，由于插入了? $-1/\omega^{2}$ ??這一項，是否 ? 是雙周期已不太明顯。然而，這是事實，且 ? 具有 2 階橢圓函數所具有的所有屬性。我們在下面定理中匯聚這些結論。

定理 1.6 函數 ? 是一個隨圓函數且具有周期 1 和 𝒯 ，并且在格點上具有雙極點。

證明：

???????? 現在只需證明 ? 是一個具有正確周期的周期函數即可。為此，注意到，對 ? 的級數逐項微分便給出了其導數，因此

$\displaystyle {\wp}^{'}(z)= -2\sum_{n,m \in \mathbb{Z}}\frac{1}{(z+n+m\tau)^{3}}$ ?。

這對我們來說完成了兩件事情。第一，只要 z 不是格點，則微分級數一致收斂，屬于引理 1.5 的 r = 3 這種情況。第二，微分也消除了減去項? $-1/\omega^{2}$ ?；因此， $\wp^{'}(z)$ ? ?這個級數顯然是雙周期函數，且以 1 和 𝒯 為周期，因為用 z + 1 和 z + 𝒯 替換 z 和，其值保持不變。

???????? 因此，存在兩個常量 a 和 b 使得

?????????????????? ?( z + 1) = ?(z) + a? 和 ?(z + 𝒯 ) = ?(z) + b 。

然而，很明顯的是，根據定義，? 是偶函數，即 ?( z ) = ?(-z) , 因為 ω∈Λ 上的和可以被 -ω∈Λ 上的和替代。因此，有 ?( -1/2) = ?(1/2)和 ?( - 𝒯/2) = ?( 𝒯/2) ，分別令 z = -1/2 和 z = - 𝒯/2 ,則在上述兩個表達式中證明了 a = b = 0 。

??? 可以不用微分而直接給出 ? 周期性的證明；見練習 4 。

1.2.2 ?? 的屬性(Properties of ? )

??? 按順序作幾條評論。首先，我們已經注意到，? 是偶函數，因此，? $\wp^{'}(z)$ ?是奇函數。由于? $\wp^{'}$ ?也是以 1 和 𝒯 為周期的周期函數，我們求得?

$\displaystyle \wp^{'}(1/2) = \wp^{'}(\tau/2) = \wp^{'}\left (\frac{1+\tau}{2} \right) = 0$ ?。

事實上，我們有(例如)

${\wp}^{'}(1/2) = -{\wp}^{'}(-1/2) = -{\wp}^{'}(-1/2 + 1) = -{\wp}^{'}(1/2)$ ?。

由于? ${\wp}^{'}$ ? 是橢圓函數且階為 3 ，這三個點 1/2，𝒯/2 ，和(1 + 𝒯 )/2(被稱為半周期(half periods))是?? ${\wp}^{'}$ ?在基礎平行四邊形中的唯一根，他們的重數均為 1 。因此，若我們定義

$\wp(1/2) = e_{1}$ ? ，? $\wp(\tau/2) = e_{2}$ ?，? 和?? $\displaystyle \wp \left (\frac{1+\tau}{2} \right ) = e_{3}$ ?，

我們推斷出方程?? $\wp( z ) = e_{1}$ ??在 1/2 處具有一個雙根。由于 ? 的階為 2，方程??? $\wp( z ) = e_{1}$ ? 在平行四邊形中不存在其它的解。類似地，方程??? $\wp( z ) = e_{2}$ ? 和?? $\wp( z ) = e_{3}$ ??分別在 𝒯/2 和 (1 + 𝒯 )/2 處具有唯一的雙根。特別是，這三個數? $e_{1}$ ?, $e_{2}$ ? 和? $e_{3}$ ?是不同的，否則，? 在基礎平行四邊形中至少會有四個根，這與 ? 的階為 2 相矛盾。從這些觀察出發，我們可以證明下面的定理。

定理 1.7 函數 $(\wp)^{2}$ ?在 ? 中是三次多項式?

$({\wp}^{'})^{2} = 4({\wp} - e_{1})( {\wp} - e_{2})( {\wp} - e_{3})$ ?。

證明：

$F(z)= 4({\wp} - e_{1})( {\wp} - e_{2})( {\wp} - e_{3})$ ?在基礎平行四邊形中的唯一根具重數 2，位于點?1/2，𝒯/2 ，和(1 + 𝒯 )/2 處。此外， $({\wp}^{'})^{2}$ ?在這些點處有雙根。而且，F 在格點處具有 6 階極點，因此， $({\wp}^{'})^{2}$ ?也是如此(因為? $\wp^{'}$ ?在那些點處具有 3 階極點)。繼而，? $({\wp}^{'})^{2}/F$ ??是全純的且仍具有雙周期，因此，這個商是常量。為了求得這個常量的值，我們注意到 0 附近的 z ，我們有?

$\displaystyle \wp( z) = \frac{1}{z^{2}} + ...$ ?和? $\displaystyle \wp^{'}( z) =\frac{-2}{z^{3}} + ...$ ? ，

其中，省略點(...) 表示更高階項。因此，這個常量是 4 , 從而定理得證。

??? 接下來，我們通過證明每一個橢圓函數都是 ? 和? $\wp^{'}$ ?的簡單組合，從而證明 ? 函數的普遍性。

定理 1.8 每一個具有周期 1 和 𝒯 的橢圓函數都是 ? 和? $\wp^{'}$ ?的比率函數(rational function)。

該定理將是其以下版本的簡單推論。

引理 1.9 每一個具有周期 1 和 𝒯 的偶橢圓函數 F 都是 ? 的比率函數。

證明：

?????? 若 F 在原點有零點或極點，則它一定是偶數階，因為 F 是偶函數。因此，存在一個?整數 m ，使得? $F{\wp}^{m}$ ?在格點具有零點或極點。故而我們可以假設 F 本身在 Λ 具有零點或極點。

我們的即刻目標就是要用 ? 來構造一個與 F 具有相同的零點和極點的雙周期函數 G 。為了實現這一點，我們回顧一下，?( z) - ?( a) 具有一個 2 階單零點(若 a 是一個半周期)，否則，函數在 a 和 – a 有兩個不同的零點。因此，我們必須存細地計數 F的零點和極點。

??? 若 a 是 F 的一個零點，則 –a 也是，因為 F 是偶函數。此外，當且僅當 F 的周期是半周期時，a 和 – a 同余，在這種情況下零點是偶數階。因此，若按重數計算的點? $a_{1} ,-a_{1},...,a_{m},-a_{m}$ ??描述了 F 的所有零點，則

? $\displaystyle [{\wp}( z) - {\wp}( a_1)]...[ {\wp}( z) - {\wp}( a_m)]$ ?

的根恰好與 F 的根相同。同樣，類似的論證(其中，?? $b_{1},-b_{1},...,b_m,-b_{m}$ ?(具有重數)(注：若? $a_{j}$ ?不是半周期，則? $a_{j}$ ? 和?? $a_{-j}$ ?在這些點具有與 F 相同的重數。若? $a_{j}$ ? 是半周期，則 ? $a_{j}$ ? ?和? $a_{-j}$ ??是同余的，則每一個都具有 F 在那些點的重數的一半))則可以證明

$\displaystyle G( z) = \frac{[{\wp}( z) - {\wp}( a_{1})]...[ {\wp}( z) - {\wp}( a_{m})]}{[{\wp}( z) - {\wp}( b_{1})]...[ {\wp}( z) - {\wp}( b_{m})]}$ ?

是周期函數，且具有與 F 相同的零點和極點。因此 F/G 是全純的且為雙周期，故而是常量。這就推斷出對引理的證明。

??? 為了證明定理，我們首先回顧到，? 是偶函數而? ${\wp}^{'}$ ?是奇函數。然后，我們將 f 寫成一個偶函數與一個奇函數之和，即

$f (z) = f_{even}( z) + f_{odd}( z)$ ?，

其中，? $\displaystyle f_{even}( z)=\frac{f(z)+f(-z)}{2}$ ?和? $\displaystyle f_{odd}( z)=\frac{f(z)-f(-z)}{2}$ ?。則，由于? $f_{odd}/\wp^{'}$ ?是偶函數，將引理應用于? $f_{even}$ ?和? $f_{odd}/\wp^{'}$ ?, 很顯然可以得到 f 是 ? 和? $\wp^{'}$ ?的比率函數。

2. 橢圓函數模特性和Eisenstein[áiz?nt?ain]級數(The modular character of elliptic functions and Eisenstein series)

??? 現在我們研究橢圓函數的模數特性，即它們基于 𝒯 的依賴性。回想一下我們在本章開頭所做的標準化。我們從兩個在 ? 上線性無關的周期? $\omega_{1}$ ?和? $\omega_{2}$ ?開始，且我們定義? $\tau=\omega_{2}/\omega_{1}$ ?。然后，我們可以假設 Im( 𝒯 ) > 0 ，此外，并假設這兩個周期是 1 和 𝒯 。接下來，我們考慮由 1 和 𝒯 所生成的晶格并構造函數 ? (具有周期 1 和 𝒯 的 2 階橢圓函數)。由于對 ? 的構造取決于 𝒯 ，因此我們可以寫成? $\wp_{\tau}$ ?以代替 ? 。這導致我們改變觀點，并主要將? $\wp_{\tau}$ ?視為 𝒯 的函數。這種方法產生了很多有趣的新見解。我們考量由以下觀察引導。首先，由于 1 和 𝒯 生成了? $\wp_{\tau}$ ?的周期，而 1 和 𝒯 + 1 生成了同樣的周期，我們可以預期?? $\wp_{\tau}$ ??和? ? $\tau_{\wp}(z+1)$ ?之間存在一種緊密的聯系。事實上，容易看出它們是恒等的。第二，由于???? $\tau=\omega_{2}/\omega_{1}$ ?，根據第 1 節開頭施加的標準化，我們發現 ? $-\tau=-\omega_{2}/\omega_{1}(\mathrm{Im}( -1/\tau ) > 0)$ ?。這實質上對應?? $\omega_{1}$ ?和? $\omega_{2}$ ?的一個交換，因此，我們也可以預期? ${\wp}_{\tau}$ ?和? ${\wp}_{-1/\tau}$ ?之間存在一種密切的關系。事實上，容易驗證??? ${\wp}_{-1/\tau}(z)=\tau^{2}{\wp}_{\tau}({\tau}z)$ ?。

因此，我們被導向去考慮上半平面 Im( 𝒯 ) > 0 的變換群(通過兩個變換 𝒯 ? 𝒯 + 1 和 𝒯 ? -1/𝒯 而生成)。我們稱這樣的群為模群(modular group)。根據我們的說法，可以預期所有本質上附加到 ? $\wp_{\tau}(z)$ ?的量都反映了上述變換。當我們考慮 Eisenstein[áiz?nt?ain](譯注： Ferdinand Eisenstein，德國數學家，1823年4月16日－1852年10月11日) 級數時，我們就可以清楚地看到這一點。

2.1? Eisenstein級數(Eisenstein series)

??? k 階 Eisenstein 級數被定義為

$\displaystyle E_{k}(\tau) = \sum_{(n,m) \ne (0,0)}\frac{1}{(n+m\tau)^{k} }$ ?(只要 k 是≥ 3 的整數和 𝒯 是復數且 Im( 𝒯 ) > 0)。

若 Λ 是由 1 和 𝒯 所生成的晶格，且若我們寫成 ω = n + m𝒯 ，則 Eisenstein 級數的另一種表達式是? $\sum_{\omega \in \Lambda^{*}}1/\omega^{k}$ ?。

定理 2.1 Eisenstein 級數具有下列屬性：

( i ) 若 k ≥ 3 則級數? $E_{k}(\tau)$ ??收斂，且在上半平面是全純的。

( ii ) 若 k 是奇數則級數? $E_{k}(\tau)=0$ ?。

( iii )?? $E_{k}(\tau)$ ?滿足下列變換關系：

$E_{k}(\tau + 1) = E_{k}(\tau)$ ?和? $E_{k}(\tau) = {\tau}^{-k} E_{k}(-1/\tau)$ ?。

這最后一個屬性有時候被稱為 Eisenstein 級數的模特征(modular character)。在下一節中，我們將會回到討論這些特征及其它模恒等式。

證明：

??? 根據引理 1.5 及其后的評注，級數 $E_{k}(\tau)$ ??在每一個復平面 Im( 𝒯 ) ≥ δ > 0 中絕對且一致收斂(只要 k ≥ 3 )；因此，? $E_{k}(\tau)$ ?在上半平面 Im( 𝒯 ) > 0 中是全純的。

??? 根據對稱性，用 –n 和 –m 替換 n 和 m ，我們可以看到，只要 k 是奇數，Eisenstein 級數恒為 0 。最后， $E_{k}(\tau)$ ?是以 1 為周期的周期函數是很顯而易見的，從事實 n + m(𝒯 + 1) = n + m + m𝒯 以及通過用 n 替代 n + m 的方式重排和式可推導出結論。此外，我們有

$(n+m(-1/\tau))^{k} = \tau^{k}(n\tau-m)^{k}$ ?，

再一次地，我們可以重排和式，這次用(n，m) 替換 (-m，n)。而結論(iii)則如下所述。

評注：

??? 由于第二個屬性的緣故，有些作者將 k 階 Eisenstein 級數定義為? $\sum_{(n,m) \ne (0,0)}1/(n+m\tau)^{2k}$ ?，可能在其前面帶一個常量因子。

當我們研究 ? 在 0 附近的級數展開式的時候，? $E_{k}$ ?與 Weierstrass ? 函數之間的聯系就出現了。

定理 2.2 對于 0 附近的 z ，我們有

$\begin{array}{rlc}{\wp} (z) &\displaystyle= \frac{1}{z^{2}} + 3E_{4}z^{2} + 5E_{6} z^4 + ... \\ \\ &\displaystyle= \frac{1}{z^{2}} + \sum_{k=1}^{\infty}(2k+1) E_{2k+2}z^{2k} \end{array}$ ?。

證明：

??? 從 ? 的定義出發，若我們注意到我們可以用 –ω 替換掉 ω 而無需改變和式，則我們有

$\displaystyle {\wp}(z)=\frac{1}{z^{2}}+\sum_{\omega \in \Lambda^{*}}\left [\frac{1}{(z+\omega)^{2}}-\frac{1}{\omega^{2}} \right ] = \frac{1}{z^{2}} +\sum_{\omega \in \Lambda^{*}}\left [\frac{1}{(z-\omega)^{2}}-\frac{1}{\omega^{2}} \right ]$ ? ,

其中，ω = n + m 𝒯 。恒等式

$\displaystyle \frac{1}{(1-w)^{2}}=\sum_{\ell=0}^{\infty}(\ell+1)\omega^{\ell}$ ?(對于 |ω| < 1 )

(上式可從微分等比級數推導出)

意味著對于任意小的 z ，

$\displaystyle \frac{1}{(1-\omega)^{2}}=\frac{1}{\omega^{2}}\sum_{\ell=0}^{\infty}(\ell+1)\left (\frac{z}{\omega} \right )^{\ell}=\frac{1}{\omega^{2}}+\frac{1}{\omega^{2}}\sum_{\ell=1}^{\infty}(\ell+1)\left (\frac{z}{\omega} \right )^{\ell}$ ? 。

因此，

$\begin{array}{rlc} \displaystyle {\wp}(z)=&\displaystyle \frac{1}{z^{2}}+\sum_{\omega \in \Lambda^{*}}\sum_{\ell=1}^{\infty}(\ell+1)\frac{z^{\ell}}{\omega^{\ell+2}} \\ \\ =&\displaystyle \frac{1}{z^{2}}+\sum_{\ell=1}^{\infty}(\ell+1)\left ( \sum_{\omega \in \Lambda^{*}}\frac{1}{\omega^{\ell+2}} \right )z^{\ell} \\ \\ =&\displaystyle \frac{1}{z^{2}}+\sum_{\ell=1}^{\infty}(\ell+1)E_{\ell+2}z^{\ell} \\ \\ =&\displaystyle \frac{1}{z^{2}}+\sum_{k=1}^{\infty}(2k+1)E_{2k+2}z^{2k} \end{array}$ ?，

其中，我們利用了? $E_{\ell+1}=0$ ?(只要 𝓁 是奇數)這個事實。

基于這個定理，我們獲得了如下三個 z 在 0 附近的展開式：

$\displaystyle {\wp}^{'}(z)=\frac{-2}{z^{3}}+6E_{4}z+20E_{6}z^{3}+...$ ?，

$\displaystyle \left ({\wp}^{'}(z)\right )^{2}=\frac{4}{z^{6}}-\frac{24E_{4}}{z^{2}}-80E_{6}+...$ ? ，

$\displaystyle \left ({\wp}^{'}(z)\right )^{3}=\frac{1}{z^{6}}-\frac{9E_{4}}{z^{2}}+15E_{6}+...$ ?。

從這些展開式出發，我們可以看到，差分函數? $({\wp}^{'} (z))^{2} - 4({\wp} (z))^{3} + 60E_4{\wp} (z) + 140E_{6}$ ?是 0 附近是全純的，事實上，在原點處等于 0 。由于這個差分函數也是雙周期的，根據定理 1.2 我們推斷出它是常量，因此其恒等于 0 。這就證明了下列的推論。

推論 2.3 若 $\displaystyle g_{2}=60E_{4}$ ?且 ? $\displaystyle g_{3}=140E_{6}$ ??,??則

$({\wp}^{'}(z))^{2} = 4{\wp}^{3} - g_{2}{\wp} - g_{3}$ ?。

注意，這個恒等式是定理 1.7 的另一個版本，它允許我們用愛 Eisenstein 級數來表達? $e_{j}$ ?的對稱函數。

2.2? Eisenstein級數和除數函數(Eisenstein series and divisor functions)

??? 現在我們將描述 Eisenstein 級數和一些數論量(number-theoretic quantities)之間的聯系。如果我們考慮周期函數? $E_{k}(\tau)$ ?的 Fourier 展開式中的 Fourier 系數，就會出現這種關系。

按等價方式，我們可以寫成? $\varepsilon(z) = E_{k}(\tau)$ ?(? $z=e^{2{\pi}i\tau}$ ?)?，并將 ? 的 Laurent 展開式作為 z 的函數研究。

??? 我們從下面的引理開始。

引理 2.4 若 k ≥ 2 且 Im( 𝒯 ) > 0 ,則

$\displaystyle \sum_{n=-\infty}^{\infty}\frac{1}{(n+\tau)^{k}}=\frac{(-2{\pi}i)^{k}}{(k-1)!}\sum_{\ell=1}^{\infty}\ell^{k-1}e^{2{\pi}i{\tau}{\ell}}$ ?。

證明：

??? 應用 Poisson 求和公式到? $f(z) = 1/(z+\tau)^{k}$ ??可推出這個恒等式；見第 4 章練習 7 。

??? 此引理的另一種證明是指出首先足以建立 k = 2 的公式，因為其他情況是通過逐項微分獲得的。為了證明這種特殊情況，我們對第 5 章中導出的余切公式進行微分，即

$\displaystyle \sum_{n=-\infty}^{\infty}\frac{1}{n+\tau}={\pi}\cot{?{\pi}\tau}$ ?。

由此得到

$\displaystyle \sum_{n=-\infty}^{\infty}\frac{1}{(n+\tau)^{2}}=\frac{?{\pi}^{k}}{\sin^{2}({\pi}\tau)}$ ???。

現在對正弦函數使用 Euler 公式，并結合事實

$\displaystyle \sum_{r=1}^{\infty}r\omega^{2}=\frac{\omega}{(1-\omega)^{2}}(\omega=e^{2{\pi}i\tau})$ ? ，

即可求得預期的結果。

??? 根據這個引理，我們可以在 Eisenstein 級數、ζ 函數和除數函數之間建立聯系。這里出現的除數函數(divisor function)? $\sigma_{\ell}(r)$ ?定義為 r 的除數的 𝓁 次冪之后，即

$\displaystyle \sigma_{\ell}(r)=\sum_{d|r}d^{\ell}$ ?。

定理 2.5 ?若 k ≥ 4 是偶數且 Im( 𝒯 ) > 0 ,則

$\displaystyle E_{k}(\tau)=2\zeta(k)+\frac{2(-1)^{k/2}(2\pi)^{k}}{(k-1)!}\sum_{r=1}^{\infty}\sigma_{k-1}(r)e^{2{\pi}i{\tau}r}$ ?。

證明：

??? 首先注意到，? $\sigma_{k-1}(r) \le rr^{k-1} = r^{k}$ ?。若 Im( 𝒯 ) = t ，則只要?? $t \ge t_{0}$ ??我們便有? $|e^{2{\pi}ir{\tau}}| \leq e^{-2{\pi}rt_{0}}$ ?，且通過將定理中的級數與? $\sum_{r=1}^{\infty}r^{k}e^{-2{\pi}rt_{0}}$ ?對比，我們可以看出，定理中的級數在任意? $t \geq t_{0}$ ?的半平面中是絕對收斂的。為了建立這個公式，我們使用 Ek?和 ζ 的定義，和 k 是偶數的事實，以及前面的引理(用 m𝒯 替代 𝒯 )而先后可得到

$\begin{array}{rlc} E_{k}(\tau)=&\displaystyle \sum_{(n,m)\ne (0,0)}\frac{1}{(n+m\tau)^{k}} \\ \\ =&\displaystyle \sum_{n \ne 0}\frac{1}{n^{k}}+\sum_{m \ne 0}\sum_{n=-\infty}^{\infty}\frac{1}{(n+m\tau)^{k}} \\ \\ =&\displaystyle 2\zeta(k)+\sum_{m \ne 0}\sum_{n=-\infty}^{\infty}\frac{1}{(n+m\tau)^{k}} \\ \\ =&\displaystyle 2\zeta(k)+2\sum_{m > 0}\sum_{n=-\infty}^{\infty}\frac{1}{(n+m\tau)^{k}} \\ \\ =&\displaystyle 2\zeta(k)+2\sum_{m > 0}\frac{(-2{\pi}i)^{k}}{(k-1)!}\sum_{\ell=1}^{\infty}{\ell}^{k-1}e^{2{\pi}im{\tau}\ell} \\ \\ =&\displaystyle 2\zeta(k)+\frac{2(-1)^{k/2}(2{\pi})^{k}}{(k-1)!}\sum_{m > 0}\sum_{\ell=1}^{\infty}{\ell}^{k-1}e^{2{\pi}im{\tau}\ell} \\ \\ =&\displaystyle 2\zeta(k)+\frac{2(-1)^{k/2}(2{\pi})^{k}}{(k-1)!}\sum_{r=1}^{\infty}{\sigma}_{k-1}(r)e^{2{\pi}i{\tau}r} \\ \\ \end{array}$ ?。

這就證明了預期的公式。

??? 最后，我們回到被“禁止”的 k = 2 這種情況。我們腦海中的級數? $\sum_{(n,m)\ne (0,0)}1/(n+m\tau)^{k}$ ?不再絕對收斂，但無論如何，我們尋求給它賦予某種意義。我們定義?

$\displaystyle F(\tau)=\sum_{m}\left ( \sum_{n}\left ( \frac{1}{(n+m\tau)^{2}} \right ) \right )$ ?，

以指定的次序求和，且(n,m) ≠ (0,0)。上述定理給出的論證證明了二重求和收斂，且事實上具有預期的表達式。

推論 2.6 ?定義 F 的按指定次序求和的雙重求和表達式收斂。我們有

$\displaystyle F(\tau)=2\zeta(2)-8{\pi}^{2}\sum_{r=1}^{\infty}\sigma(r)e^{2{\pi}ir{\tau}}$ ?，

其中，? $\sigma(r)=\sum_{d|r}{d}$ ?是 r 的除數之和。

可以看出，? $F(-1/\tau ) {\tau}^{-2}$ ?不等于 F( 𝒯 ) ,這等同于稱，對于 F 的雙重級數，當我們先按 m 再按 n 求和時，會得出不同的值(? $\tilde{F}$ ?， $F$ ?的逆)。事實證明，盡管如此，被禁止的Eisenstein 級數(forbidden Eisenstein series) F( 𝒯 ) 仍然可以在證明有關將整數表示為四個平方和的著名定理中以至關重要的方式使用。我們將在下一章討論這些問題。