前言
群體遺傳學是研究生物群體中基因的分布、基因頻率和基因型頻率的維持和變化的學科。它不僅探討遺傳病的發病頻率和遺傳方式,還研究基因頻率和變化的規律,為預防、監測和治療遺傳病提供重要信息。R語言作為一種強大的統計分析工具,在群體遺傳學研究中扮演著不可或缺的角色。它提供了多種包和函數,使得復雜的遺傳數據分析變得簡單高效。本教程參考《Population genetics with R》
對于R語言的基礎,我寫過一些博客,可以先看R語言入門的教學
【R語言從0到精通】-1-下載R語言與R最基礎內容-CSDN博客
R語言Matrix快速review
矩陣運算對于計算生物學的計算或者生物的計算來說是非常重要的。
現在你應該已經有配置好的Rstudio,然后熟悉基本的指令,那么現在我們學習一些學習本教程所需要的R語言小知識:對于Matrix操作及計算
1.Matrix建立
與數據框不同,R中的矩陣只接受相同類別的元素。因此,你不能擁有一個同時包含數字和因子(分類變量)的單一矩陣,只能包含其中一種。
# 創建一個3x3的矩陣,元素為1到9
mat <- matrix(1:9, nrow = 3, ncol = 3)# 打印矩陣
print(mat)得到3*3矩陣:

如果我們使用byrow這個參數,會得到一個不一樣的矩陣,因為是按x填充的:
mat2 <- matrix(1:9, nrow = 3, ncol = 3, byrow = T)
print(mat2)
2.R語言matrix簡單乘法
我們創立一個小矩陣,進行自乘的矩陣運算
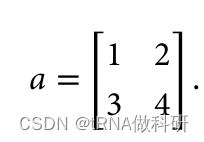
矩陣乘法的公式是:
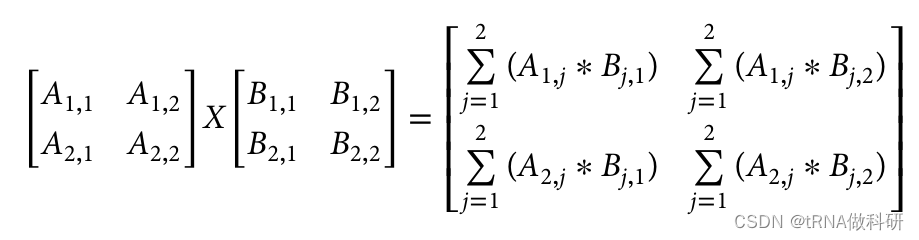
使用R語言得到:

而我們通過數學計算得到的是:
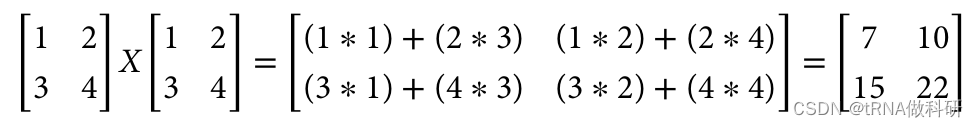
不一樣的原因是R語言的矩陣乘法并不是簡單的*,而是A %*% B
那我們在R語言中Matrix的*是描述什么運算呢?是對應位置的乘法,因此要求兩個矩陣的行列數量是一樣的,也就是:

好了,主要是為了講一下矩陣的乘法在R語言中怎么用,接下來我們正式開始。
Hardy–Weinberg genotype proportions
1.一些名詞
Allele: 等位基因:一種遺傳變異(位于一對同源染色體相同位置上控制同一性狀不同形態的基因)
Diploid: 二倍體:具有所有(大部分)遺傳物質的兩個副本的個體。
Haploid: 單倍體:具有所有遺傳物質的一個副本的個體。
Heterozygote: 雜合子:具有不同等位基因副本的個體。
Homozygote: 純合子:具有相同等位基因副本的個體。
Genotype: 基因型:個體中等位基因的組合。
Locus: 基因座:等位基因的物理位置,復數形式為 loci。
Phenotype: 表型:基因型(和非遺傳影響)的結果
2.群體遺傳學簡介
我將以通俗的語言講述我對于群體遺傳學的理解,希望大家能喜歡。
群體遺傳學是一門研究群體中遺傳信息傳遞和變化的科學。主要關注種群中遺傳變異的模式,以及這些變異是如何隨時間演變的。通俗地說,群體遺傳學家就像是在玩一個大型的拼圖游戲,我們試圖弄清楚每個拼圖片(即遺傳變異或等位基因)在整個種群中的分布情況。
(1)首先,讓我們來談談“預計有多少個體攜帶某一特定等位基因”的問題。想象一下,我們有一盒五顏六色的積木,每種顏色的積木代表一種特定的等位基因。如果我們隨機從盒子里拿出一塊積木,我們可能會想知道拿出某種特定顏色積木的概率是多少。在群體遺傳學中,這個概率可以通過查看該等位基因在種群中的頻率來估計。如果一個等位基因在種群中很常見,那么攜帶它的個體數量就會相對較多;相反,如果它是罕見的,那么攜帶它的個體就會較少。
(2)“找到罕見突變兩個副本的可能性有多大”這個問題,可以比作是從積木盒子里連續拿出兩塊相同稀有顏色的積木的概率。因為罕見突變的等位基因在種群中出現的頻率很低,所以同時拿到兩個這樣的副本的幾率會非常小。這個概率可以通過計算該等位基因頻率的平方來估計,因為每次復制事件都是獨立的。
(3)“某一特定基因型來自一個人群或另一個人群的可能性有多大”這個問題,可以想象成我們有一堆分別來自不同人群的積木,每堆積木中各種顏色(即基因型)的比例可能不同。當我們看到一個特定顏色的積木時,我們可能會好奇它最有可能來自哪一堆。這個可能性可以通過比較不同人群中該基因型的頻率來確定。 有了這些基本的頻率和概率預期之后,群體遺傳學家就可以開始尋找實際觀察到的遺傳模式與預期之間的偏差。這些偏差可以提供有關種群歷史、遷移事件、自然選擇作用以及其他影響遺傳變異分布的因素的重要線索。通過分析這些偏差,科學家們可以對種群的過去、現在和未來做出更加有根據的預測,就像是通過拼圖的碎片逐漸揭示出整個畫面的過程。
3.等位基因與SNP
等位基因在經典遺傳學中被定義為導致不同表型的基因變體,可以是雜合子或純合子。然而,在現代遺傳學的語境中,等位基因的概念被擴展到包括基因組內特定位點或位置的任何遺傳變異,不論這種變異是否對基因功能或生物體的表型產生影響。 一種特別普遍的遺傳變異類型是單核苷酸多態性(SNP)。SNP發生在DNA序列中單個核苷酸的位置上,其中一個核苷酸在不同的個體中存在差異。例如,如果某個DNA序列的一部分原本是...GTAG[C]TAGAC...,而在另一個個體中這一部分變成了...GTAG[T]TAGAC...這就構成了一個SNP。 當我們在多個個體間比較這段DNA序列時,會發現括號內的位置存在兩種可能的核苷酸(C或T),這表明這個位點是一個多態性位點,擁有兩個相關的等位基因。 在二倍體生物中,每個細胞包含兩組染色體,因此每個基因位點上有兩個等位基因。這意味著在考慮一個具有兩個等位基因的位點時,可能存在三種不同的基因型:純合子CC、雜合子CT和另一種純合子TT。這種分類對于理解遺傳變異如何在種群中分布以及它們如何可能影響生物體的性狀至關重要。
4.等位基因頻率
假設T等位基因在某個群體中頻率為p(0-1)。當我們從這個群體中隨機抽取一個等位基因時,抽到T等位基因的概率就是p。 如果T等位基因的頻率是1/2,那么在一個沒有額外親本基因型信息的隨機情況下,一個個體從一個親本那里繼承到這個T等位基因副本的概率也是1/2。這是因為每個親本都有相等的機會傳遞T或非T等位基因。 進一步考慮到新一代的個體,預計其中一半會從他們的一個親本那里繼承到T等位基因。由于每個親本傳遞特定等位基因的概率獨立,新一代中的某些個體還有可能從另一個親本那里也繼承到T等位基因,這個概率同樣是1/2。 因此,在新一代的所有個體中,預計有一半的一半,即1/4的個體將會是兩個T等位基因的純合子。這些純合子的頻率可以用數學表達式p × p = p^2來表示。 這里隱含的假設是,這些遺傳變異是按照隨機的方式傳遞的。 在模擬隨時間推移的群體遺傳學時,我們需要做出許多這樣的假設,以便簡化模型并使問題可解。
5.Hardy–Weinberg genotype proportions
我們可以從觀察到的基因型頻率反推預期的等位基因頻率。一些遺傳變異在純合子時會產生隱性表型。假設我們在一個人群中觀察到具有新的突變等位基因的純合子,其頻率為1/1000,也就是p方
f <- 1/1000
sqrt(f)接下來我們考慮雜合子的情況:
如果繼承一個等位基因的概率是p,那么不繼承它的概率就是1-p。因為我們在這里只關注雜合子的情況,這些個體要么從母親那里繼承了一個等位基因副本,但沒有從父親那里繼承,概率為p(1-p),要么沒有從母親那里繼承副本,但從父親那里繼承了,概率也為(1-p)p。這兩個事件是互斥的:為了使個體成為攜帶者,突變等位基因要么來自母親,要么來自父親。因此,我們使用概率的“或”(加法)規則,將不同的結果相加:p(1-p) + (1-p)p = 2p(1-p)。
這些關于p2純合子頻率和2p(1-p)雜合子頻率的預期被稱為哈代-溫伯格基因型比例。
我們可以通過R語言curve函數來可視化純合子情況
curve(x^2, 0, 1, xlab = "Allele Frequency", ylab = "Genotype Frequency", lwd = 3,col = "green")
text(0.6, 0.2, "Homozygotes",col = "green")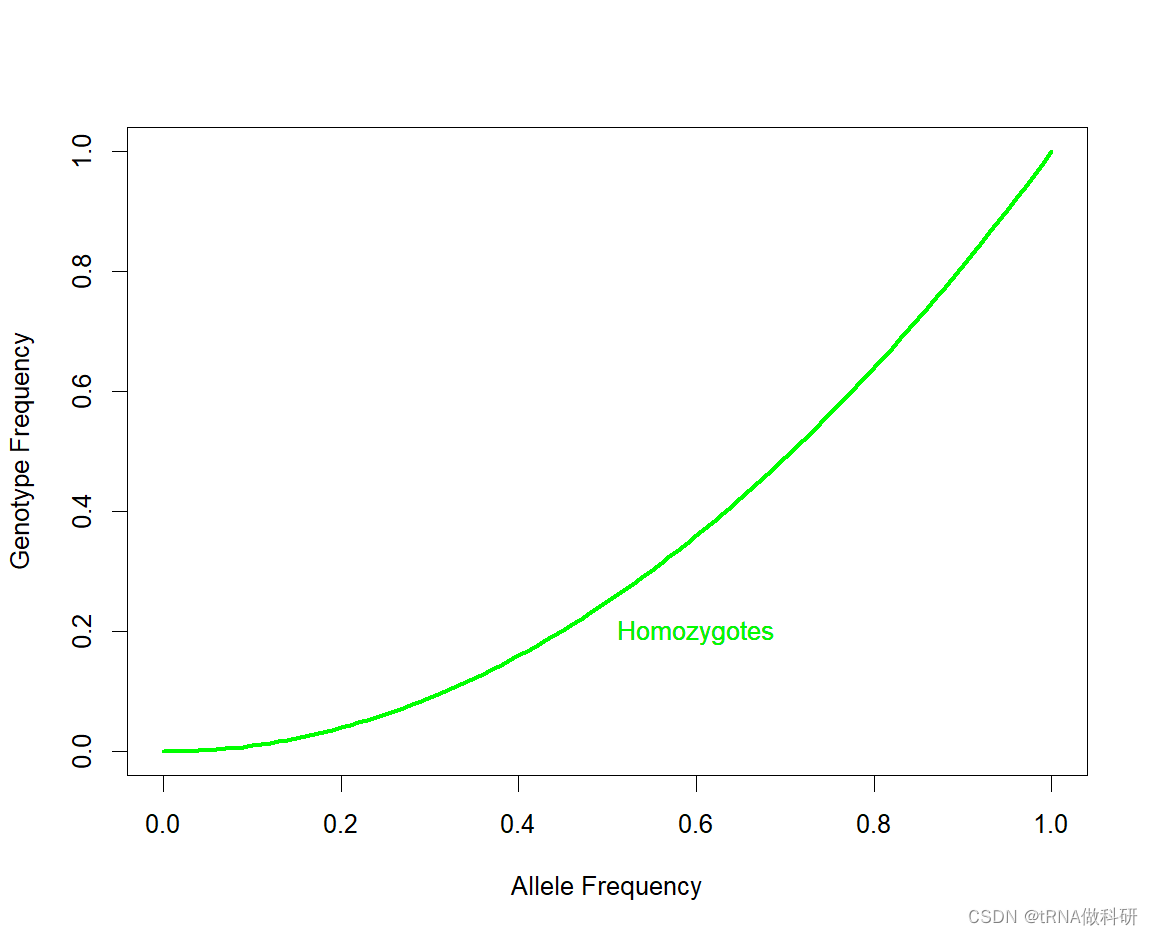
我們再加入雜合子的情況:
curve(2*x*(1-x), 0, 1, add=TRUE, xlab="Allele frequencies",ylab="Genotype frequencies", col="blue", lwd=2)
text(0.25, 0.5, "Heterozygotes", col="blue")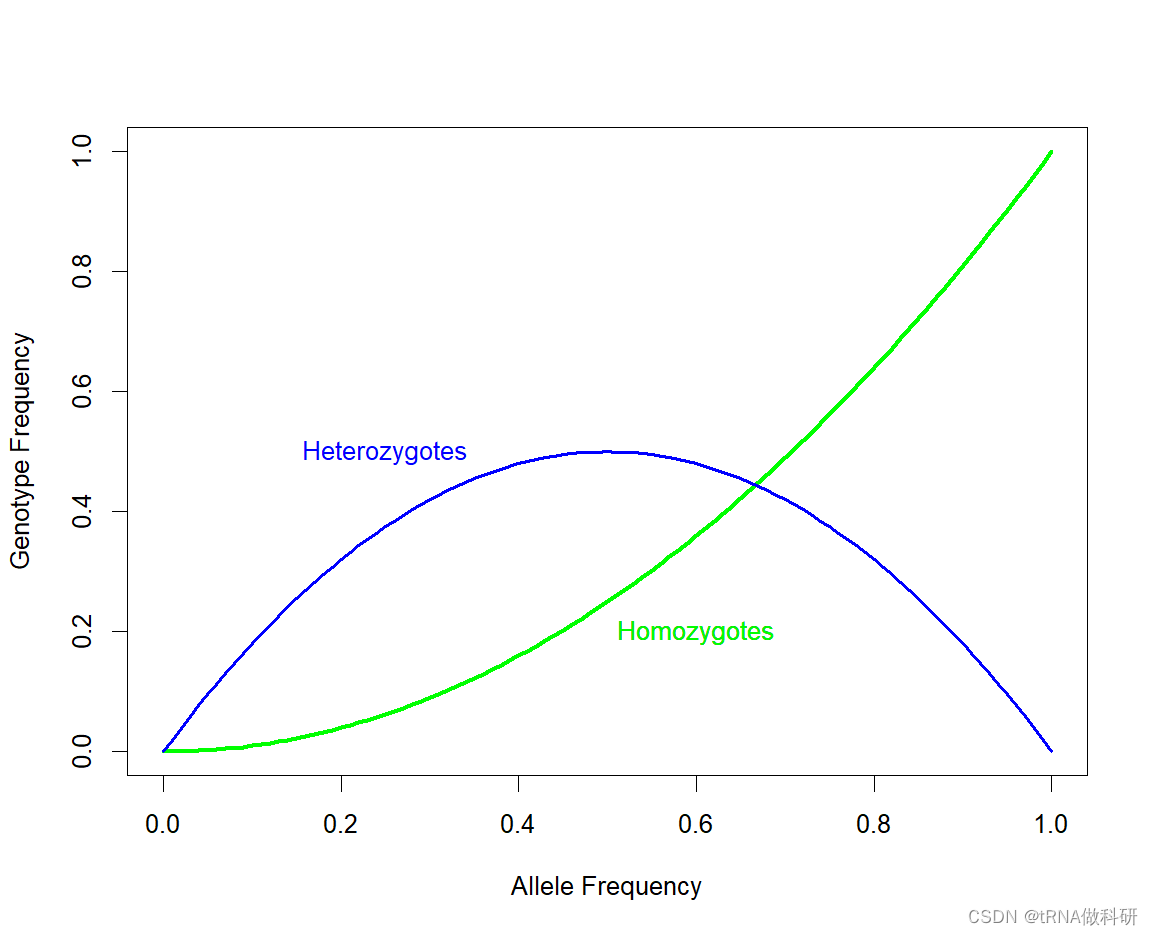
我們看到隨著等位基因頻率增加,雜合子和純合子的頻率預期不同。隨等位基因頻率的增加,雜合子的數量最初比純合子的數量增長得更快。但是,當你的等位基因頻率接近50%時,雜合子的數量趨于穩定,一旦大部分人口(超過50%)攜帶這個等位基因,更多的個體開始以純合子的形式攜帶兩份拷貝,而不是以雜合子的形式只攜帶一份拷貝。當一個等位基因頻率達到1.0(100%)時,這個等位基因被認為在種群中“固定”了。一旦發生這種情況,它只能存在于純合子個體中,因為沒有其他變異等位基因存在。當一個等位基因頻率達到0%時,這個等位基因被認為是“丟失”了。
在圖中我們可以看到一個兩曲線相交的點,也就是:![]()
可以解得p=2/3。我們在圖上標記:
p <- 2/3
points(p,p^2,lwd=2,cex=2)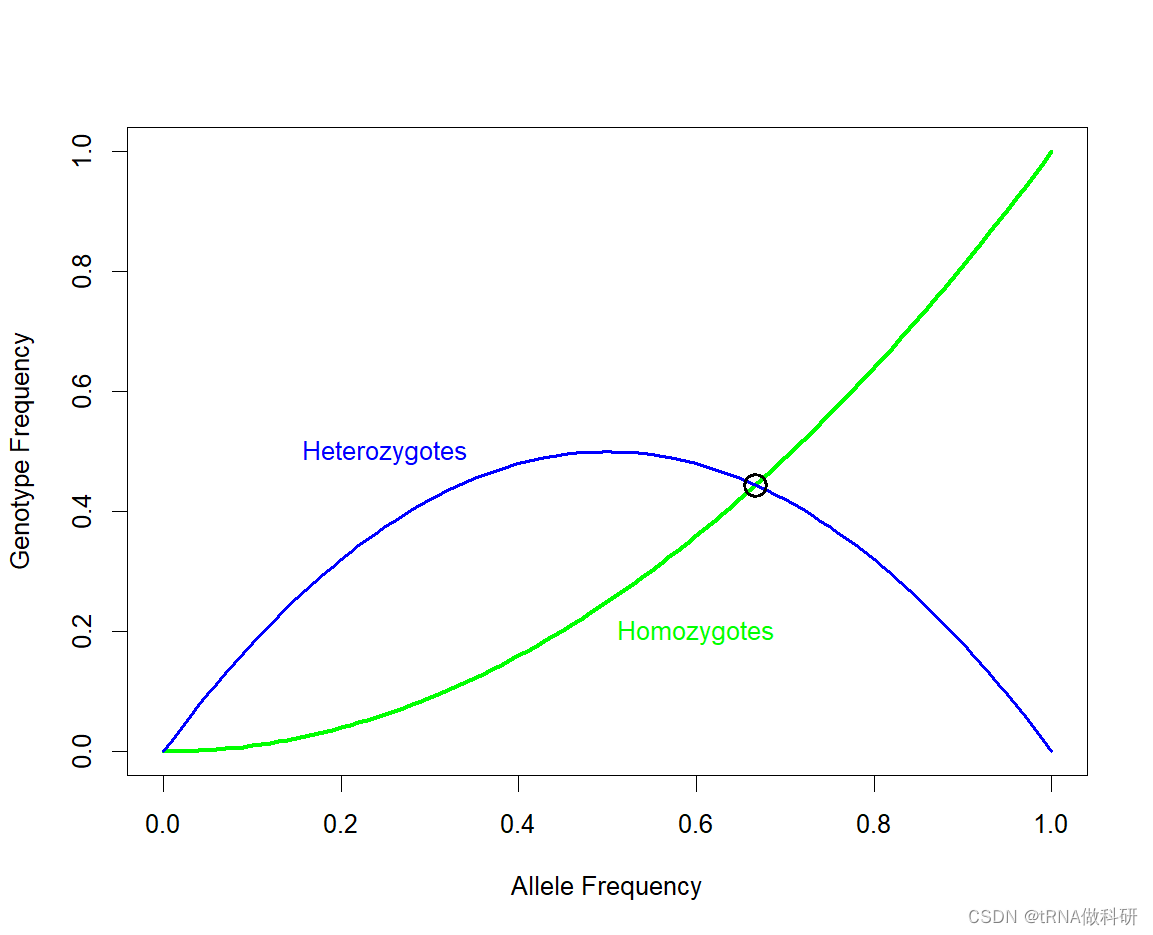
本次內容先寫這么多,下一章講simulateing genotype內容,歡迎大家在評論區討論。




)


)


—網絡加固—防DNS污染和ARP欺騙)


)





