《昇思25天學習打卡營第6天 | 函數式自動微分》

函數式自動微分

神經網絡的訓練主要使用反向傳播算法，模型預測值（logits）與正確標簽（label）送入損失函數（loss function）獲得loss，然后進行反向傳播計算，求得梯度（gradients），最終更新至模型參數（parameters）。自動微分能夠計算可導函數在某點處的導數值，是反向傳播算法的一般化。自動微分主要解決的問題是將一個復雜的數學運算分解為一系列簡單的基本運算，該功能對用戶屏蔽了大量的求導細節和過程，大大降低了框架的使用門檻。

MindSpore使用函數式自動微分的設計理念，提供更接近于數學語義的自動微分接口grad和value_and_grad。

簡單的單層線性變換模型

我們通過學習使用一個簡單的單層線性變換模型來了解

import numpy as np
import mindspore
from mindspore import nn
from mindspore import ops
from mindspore import Tensor, Parameter

函數與計算圖

計算圖是用圖論語言表示數學函數的一種方式，也是深度學習框架表達神經網絡模型的統一方法。我們將根據下面的計算圖構造計算函數和神經網絡。

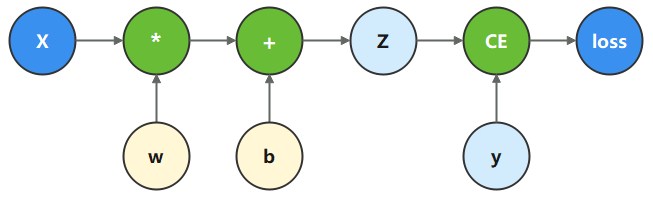
在這個模型中， 𝑥
為輸入， 𝑦
為正確值， 𝑤
和 𝑏
是我們需要優化的參數。

x = ops.ones(5, mindspore.float32)  # input tensor
y = ops.zeros(3, mindspore.float32)  # expected output
w = Parameter(Tensor(np.random.randn(5, 3), mindspore.float32), name='w') # weight
b = Parameter(Tensor(np.random.randn(3,), mindspore.float32), name='b') # bias

我們根據計算圖描述的計算過程，構造計算函數。 其中，binary_cross_entropy_with_logits 是一個損失函數，計算預測值和目標值之間的二值交叉熵損失。

def function(x, y, w, b):z = ops.matmul(x, w) + bloss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))return loss

執行計算函數，可以獲得計算的loss值。

loss = function(x, y, w, b)
print(loss)

Tensor(shape=[], dtype=Float32, value= 0.914285)

微分函數與梯度計算

為了優化模型參數，需要求參數對loss的導數：$\frac{?\mathrm{loss}}{?w}$和$\frac{?\mathrm{loss}}{?b}$，此時我們調用mindspore.grad函數，來獲得function的微分函數。

這里使用了grad函數的兩個入參，分別為：

• fn：待求導的函數。
• grad_position：指定求導輸入位置的索引。

由于我們對$w$和$b$求導，因此配置其在function入參對應的位置(2, 3)。

使用grad獲得微分函數是一種函數變換，即輸入為函數，輸出也為函數。

grad_fn = mindspore.grad(function, (2, 3))

執行微分函數，即可獲得 𝑤
、 𝑏
對應的梯度。

grads = grad_fn(x, y, w, b)
print(grads)

(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01],
[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01],
[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01],
[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01],
[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01]]),
Tensor(shape=[3], dtype=Float32, value= [ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01]))

Stop Gradient

通常情況下，求導時會求loss對參數的導數，因此函數的輸出只有loss一項。當我們希望函數輸出多項時，微分函數會求所有輸出項對參數的導數。此時如果想實現對某個輸出項的梯度截斷，或消除某個Tensor對梯度的影響，需要用到Stop Gradient操作。

這里我們將function改為同時輸出loss和z的function_with_logits，獲得微分函數并執行。

def function_with_logits(x, y, w, b):z = ops.matmul(x, w) + bloss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))return loss, z

grad_fn = mindspore.grad(function_with_logits, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)

(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00],
[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00],
[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00],
[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00],
[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00]]),
Tensor(shape=[3], dtype=Float32, value= [ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00]))

可以看到求得$w$、$b$對應的梯度值發生了變化。此時如果想要屏蔽掉z對梯度的影響，即仍只求參數對loss的導數，可以使用ops.stop_gradient接口，將梯度在此處截斷。我們將function實現加入stop_gradient，并執行。

def function_stop_gradient(x, y, w, b):z = ops.matmul(x, w) + bloss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))return loss, ops.stop_gradient(z)

grad_fn = mindspore.grad(function_stop_gradient, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)