LeetCode-刷題記錄-二分法合集（本篇blog會持續更新哦~）

一、二分查找概述

二分查找（Binary Search）是一種高效的查找算法，適用于有序數組或列表。（但其實只要滿足二段性，就可以使用二分法，本篇博客后面博主會持續更新一些題，來破除一下人們對“只有有序才能二分”的誤解。）

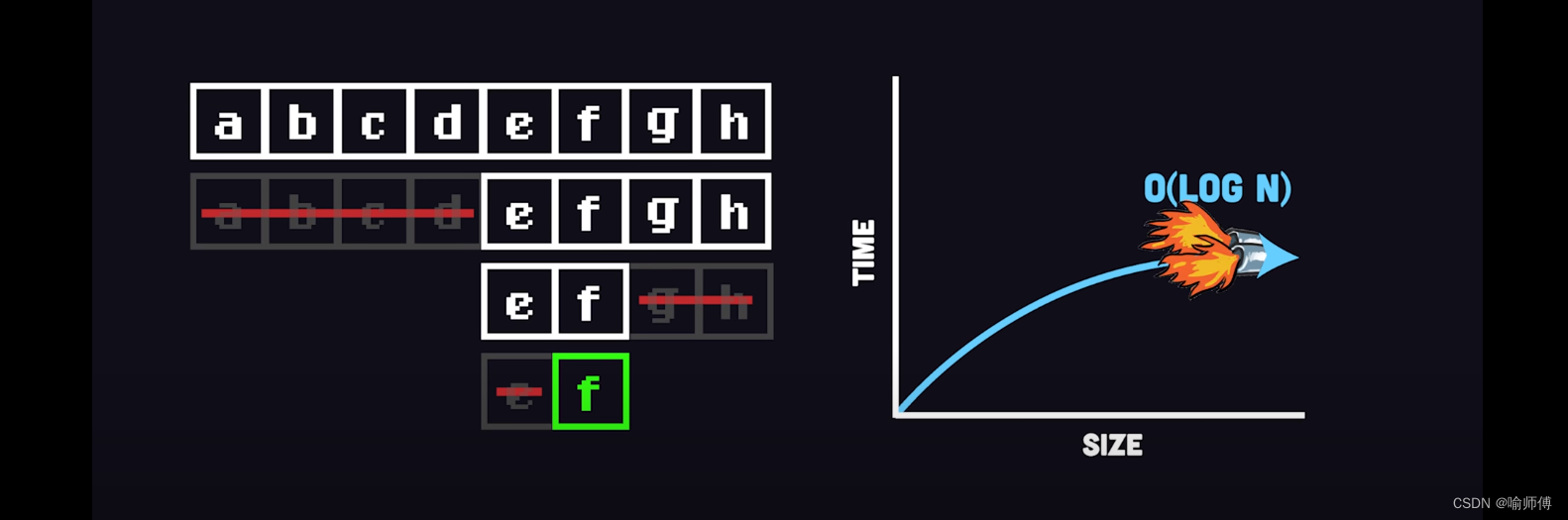
在這里插入圖片描述

二分通過反復將查找范圍分為兩半，并根據目標值與中間元素的大小關系來確定下一步查找的方向，從而快速定位目標值的位置。

二、二分法代碼實現

三、二分法習題合集

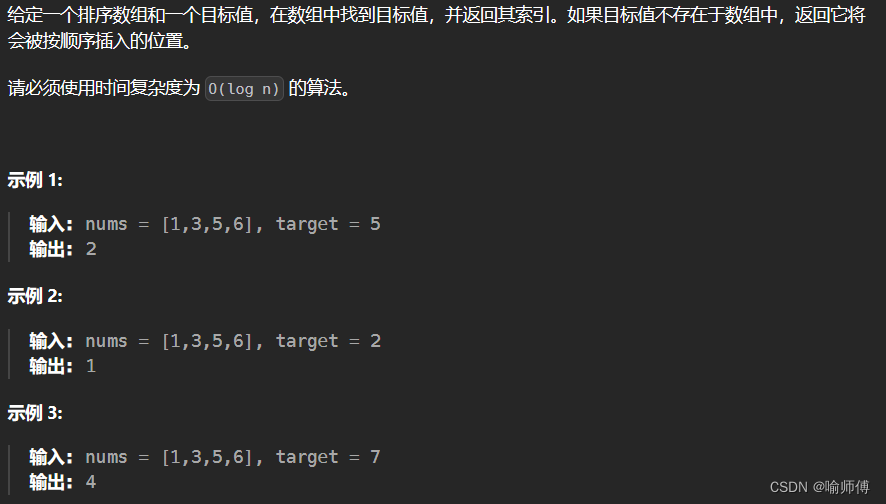
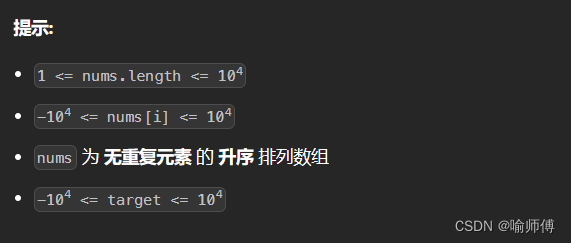
1.LeetCode 35 搜索插入位置

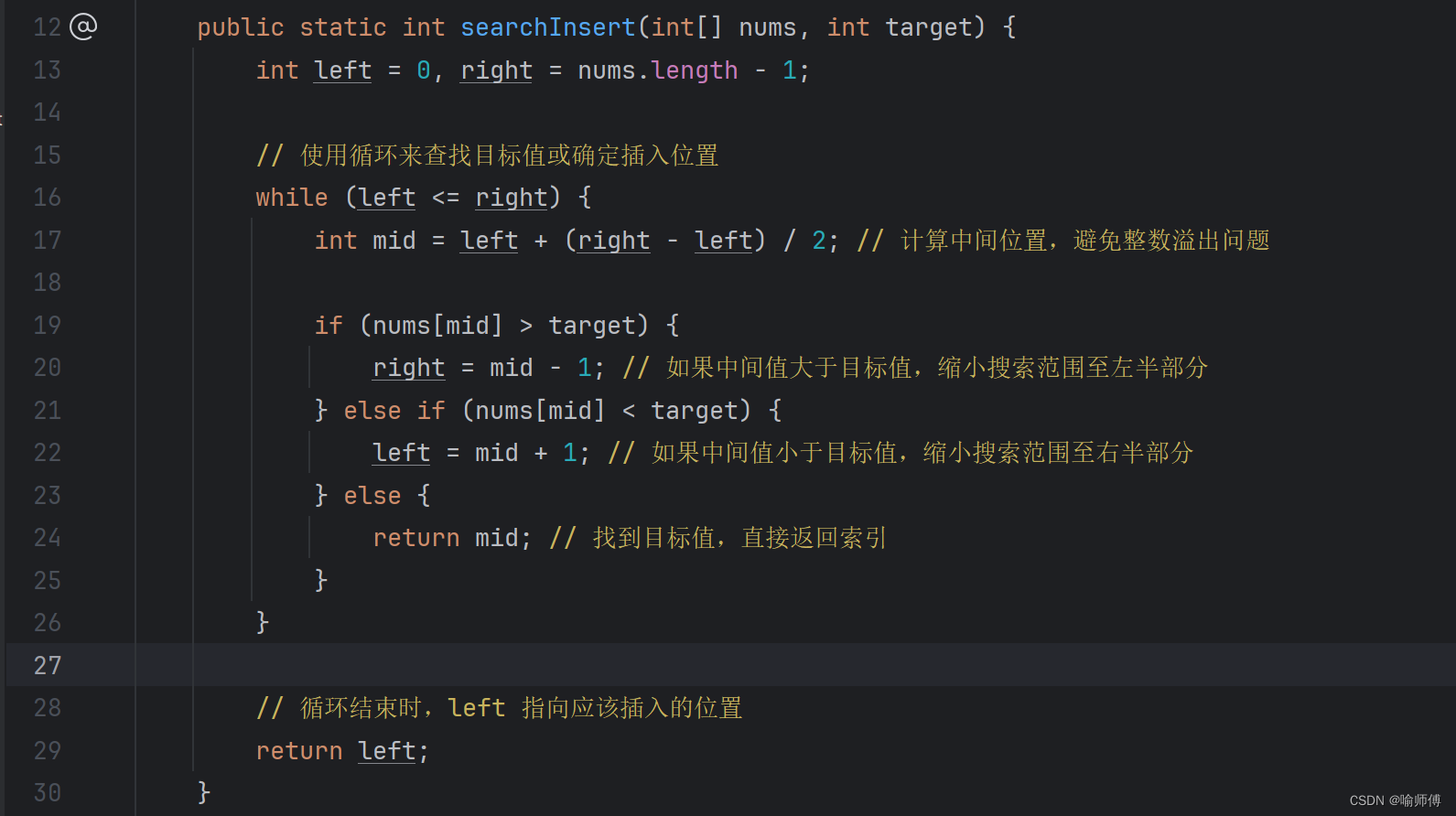
在這里插入圖片描述

解法

在這里插入圖片描述

public static int searchInsert(int[] nums, int target) {int left = 0, right = nums.length - 1;// 使用循環來查找目標值或確定插入位置while (left <= right) {int mid = left + (right - left) / 2; // 計算中間位置，避免整數溢出問題if (nums[mid] > target) {right = mid - 1; // 如果中間值大于目標值，縮小搜索范圍至左半部分} else if (nums[mid] < target) {left = mid + 1; // 如果中間值小于目標值，縮小搜索范圍至右半部分} else {return mid; // 找到目標值，直接返回索引}}// 循環結束時，left 指向應該插入的位置return left;
}

這里博主解釋一下為什么最后返回left（debug走一下流程或者在草稿紙上畫一畫其實就很容易看出來啦~）。

函數 searchInsert 的目標是在給定的有序數組 nums 中查找目標值 target 的插入位置（如果目標值不存在于數組中）。

如果數組中存在目標值，則返回目標值的索引；如果不存在，則返回應該插入的位置索引，使得插入后數組依然保持有序。

插入位置保持有序性：

返回 left 而不是 right 是因為當循環結束時，left 恰好指向比 target 大的第一個元素的位置，或者數組的末尾位置（如果 target 大于數組中的所有元素），這正是目標值應該插入的位置，可以保持數組的有序性。

2.LeetCode 69 x的平方

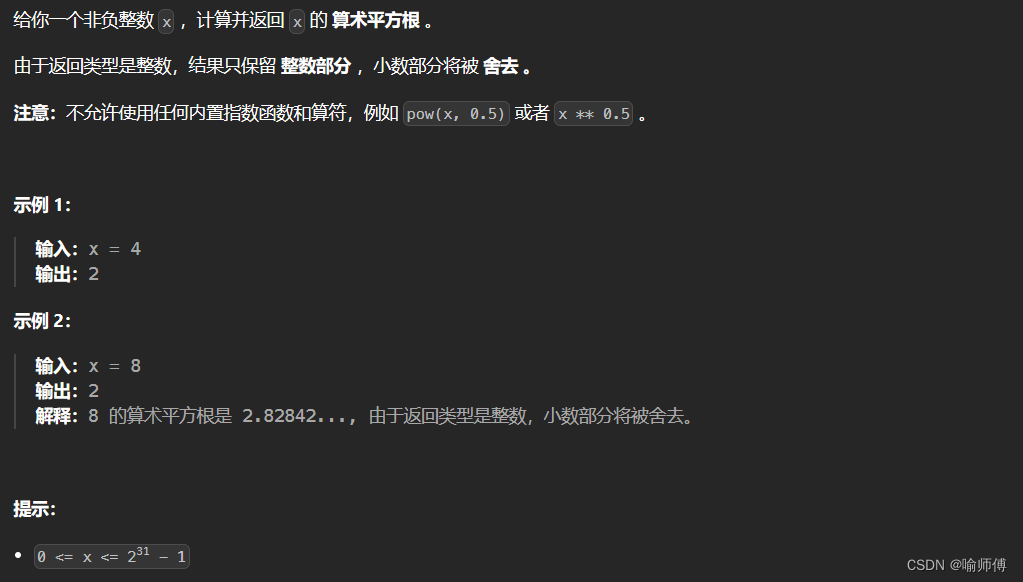
在這里插入圖片描述

解法

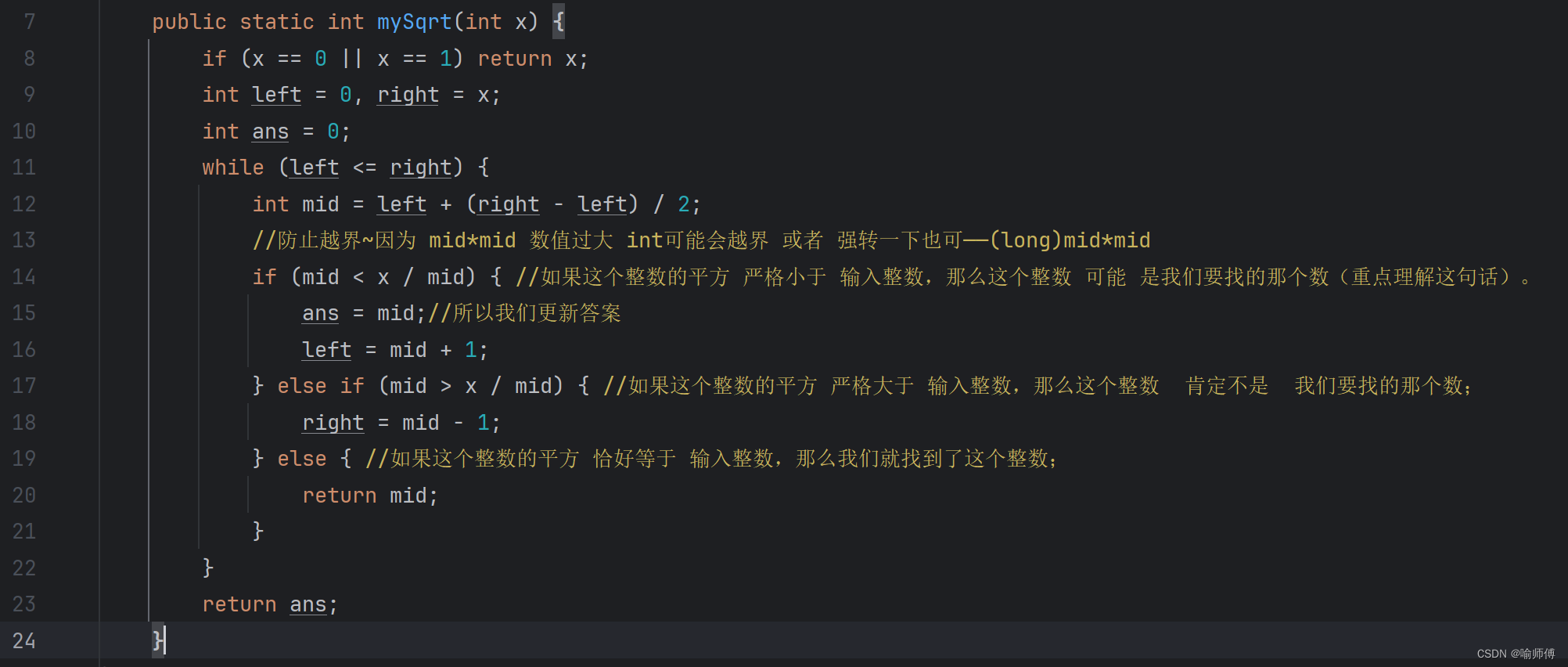
在這里插入圖片描述

public static int mySqrt(int x) {if (x == 0 || x == 1) return x;int left = 0, right = x;int ans = 0;while (left <= right) {int mid = left + (right - left) / 2;//防止越界~因為 mid*mid 數值過大 int可能會越界 或者 強轉一下也可——(long)mid*midif (mid < x / mid) { //如果這個整數的平方 嚴格小于 輸入整數，那么這個整數 可能 是我們要找的那個數（重點理解這句話）。ans = mid;//所以我們更新答案left = mid + 1;} else if (mid > x / mid) { //如果這個整數的平方 嚴格大于 輸入整數，那么這個整數  肯定不是  我們要找的那個數；right = mid - 1;} else { //如果這個整數的平方 恰好等于 輸入整數，那么我們就找到了這個整數；return mid;}}return ans;}

3.LeetCode 367 有效的完全平方數

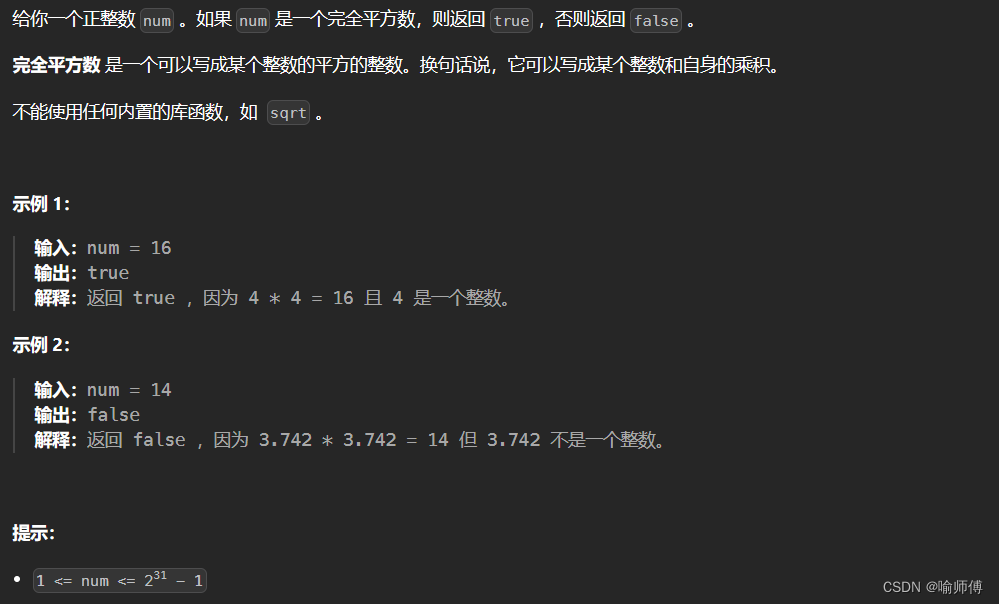
在這里插入圖片描述

解法

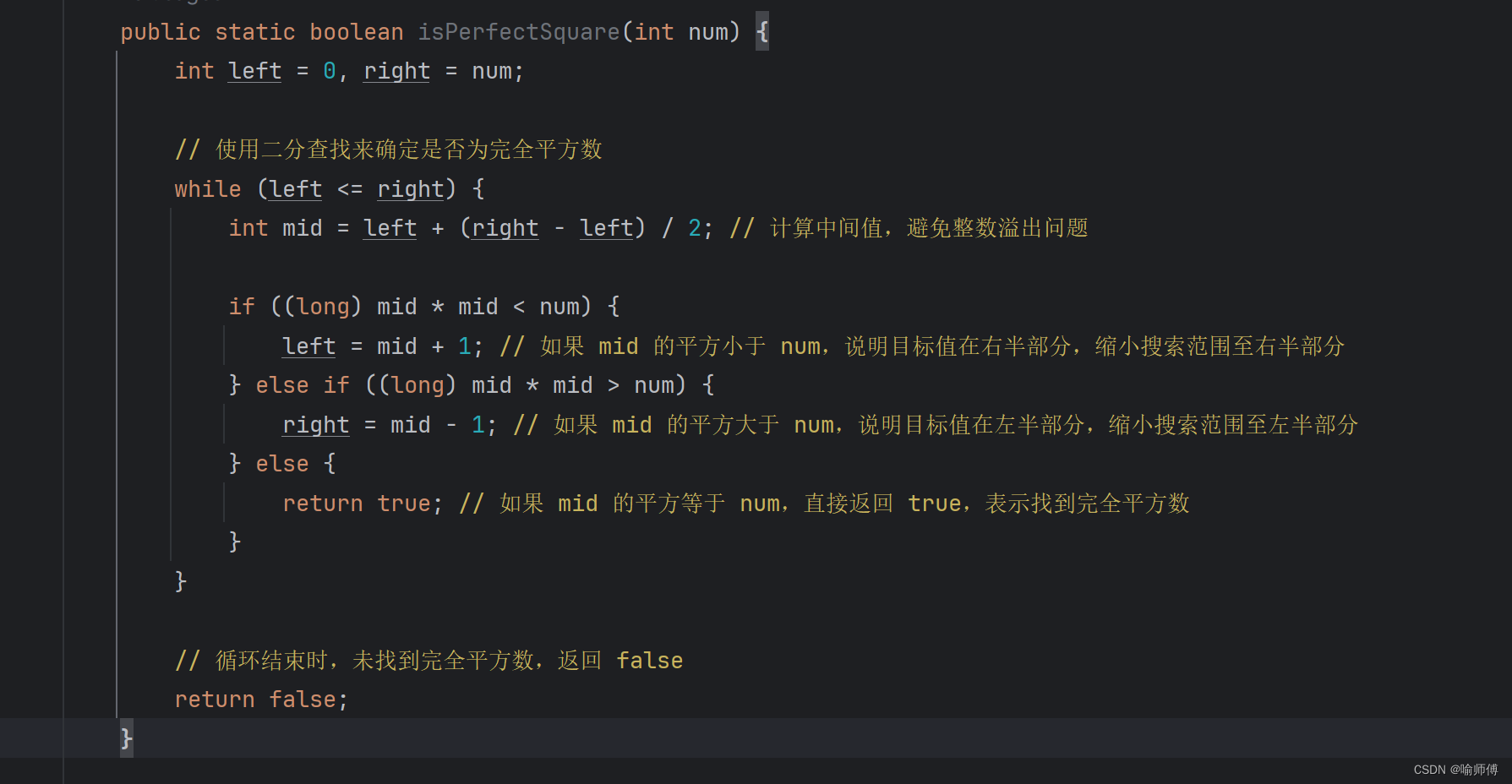
在這里插入圖片描述

public static boolean isPerfectSquare(int num) {int left = 0, right = num;// 使用二分查找來確定是否為完全平方數while (left <= right) {int mid = left + (right - left) / 2; // 計算中間值，避免整數溢出問題if ((long) mid * mid < num) {left = mid + 1; // 如果 mid 的平方小于 num，說明目標值在右半部分，縮小搜索范圍至右半部分} else if ((long) mid * mid > num) {right = mid - 1; // 如果 mid 的平方大于 num，說明目標值在左半部分，縮小搜索范圍至左半部分} else {return true; // 如果 mid 的平方等于 num，直接返回 true，表示找到完全平方數}}// 循環結束時，未找到完全平方數，返回 falsereturn false;
}

4.LeetCode 34 在排序數組查找元素的第一個和最后一個位置

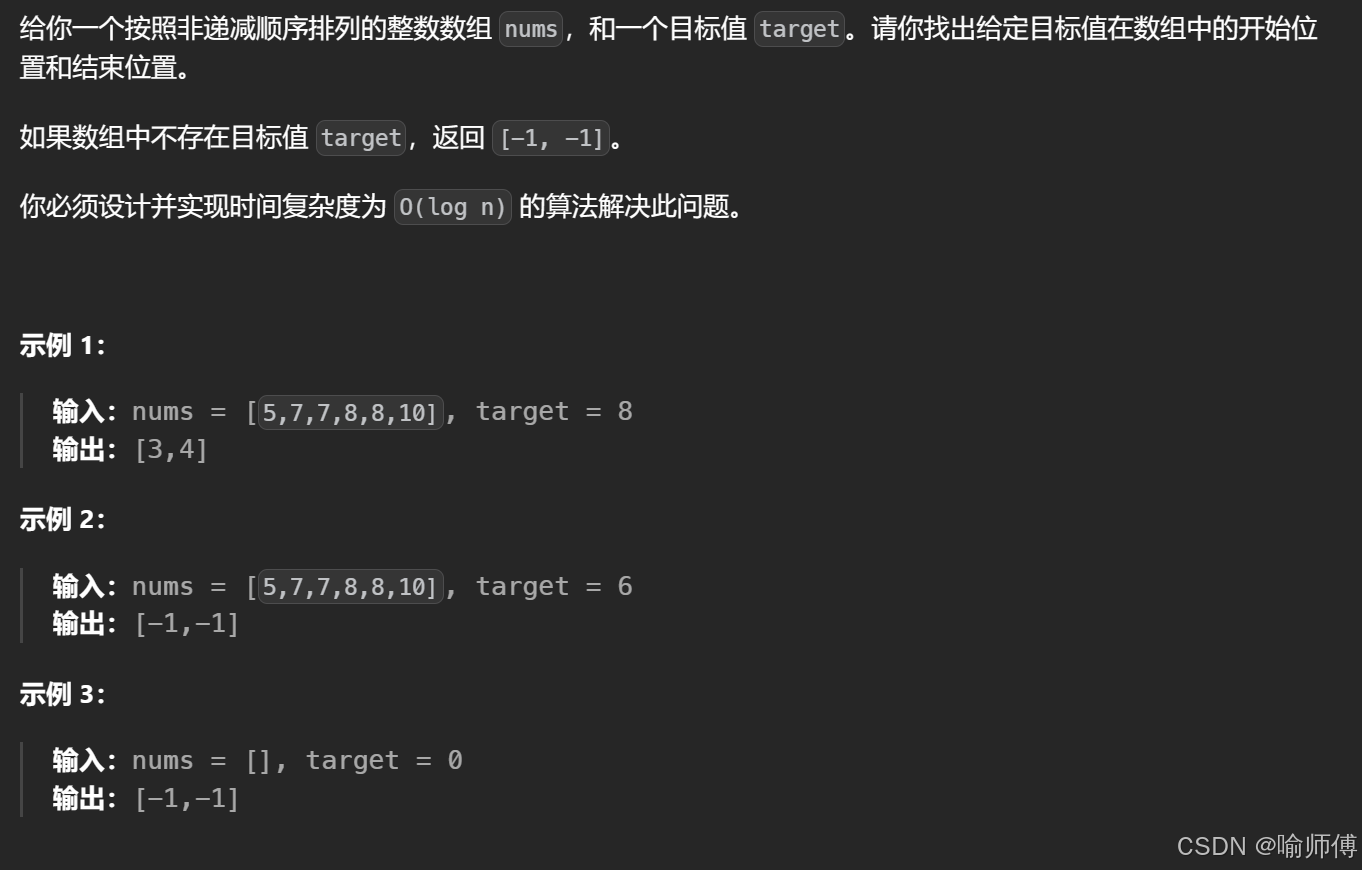
在這里插入圖片描述

解法

本題拆分成兩個函數，分別處理較好，不過這個對處理二分的熟練度要求還挺高，比如說left<=right 還是left<right以及左右指針什么時候該怎么移動都有講究，一個小細節不對的話就得不到正確的答案。

大概的二分的模版大家都知道，區別就在于具體問題的邊界問題，是需要自己思考的。

建議有電腦的小伙伴可以debug走一下流程，可以看出來左右指針怎么移動的，慢慢調試；或者在紙上畫一畫，看一看自己寫的二分是怎么個流程~

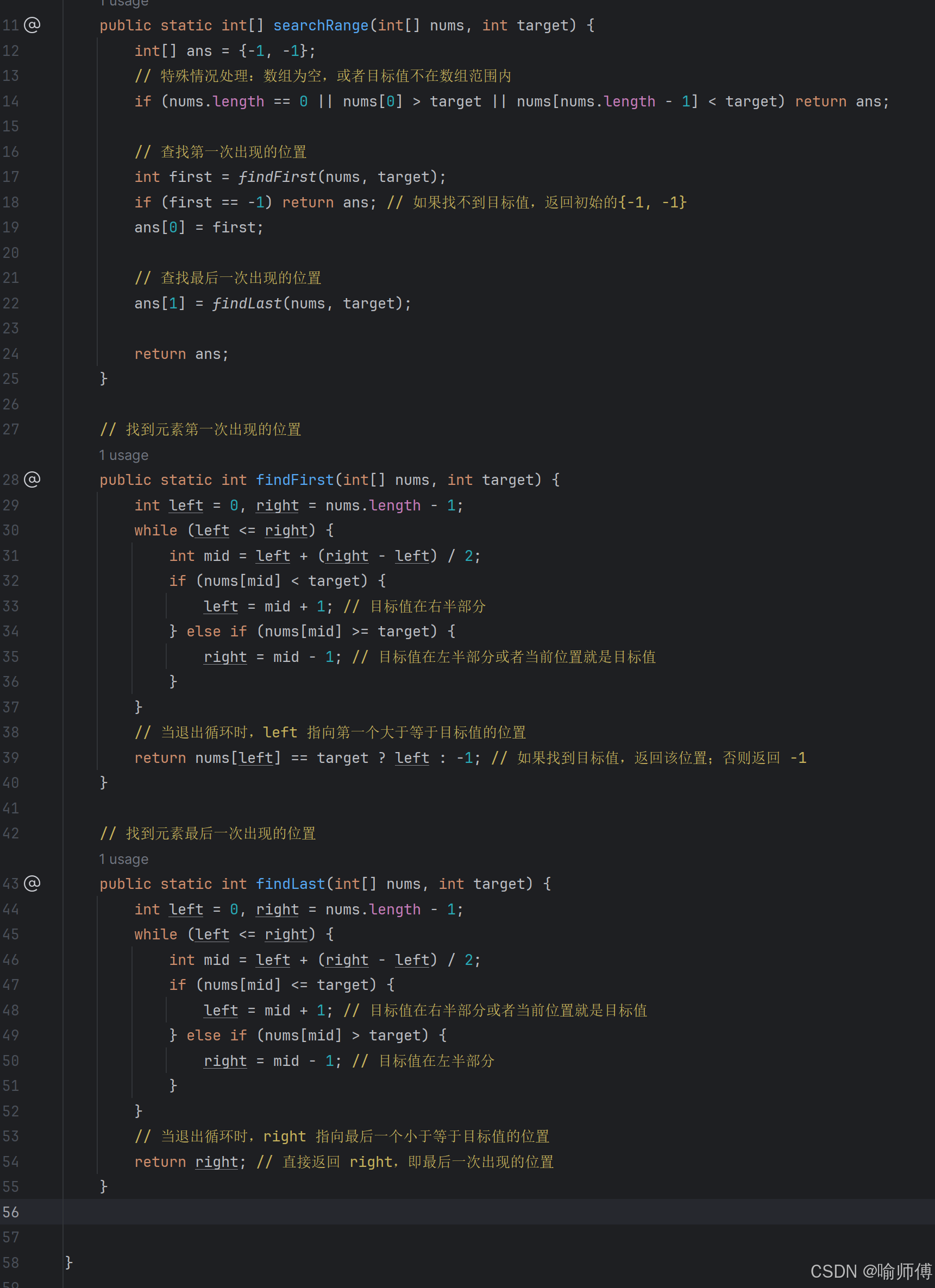
在這里插入圖片描述

public static int[] searchRange(int[] nums, int target) {int[] ans = {-1, -1};// 特殊情況處理：數組為空，或者目標值不在數組范圍內if (nums.length == 0 || nums[0] > target || nums[nums.length - 1] < target) return ans;// 查找第一次出現的位置int first = findFirst(nums, target);if (first == -1) return ans; // 如果找不到目標值，返回初始的{-1, -1}ans[0] = first;// 查找最后一次出現的位置ans[1] = findLast(nums, target);return ans;
}// 找到元素第一次出現的位置
public static int findFirst(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1; // 目標值在右半部分} else if (nums[mid] >= target) {right = mid - 1; // 目標值在左半部分或者當前位置就是目標值}}// 當退出循環時，left 指向第一個大于等于目標值的位置return nums[left] == target ? left : -1; // 如果找到目標值，返回該位置；否則返回 -1
}// 找到元素最后一次出現的位置
public static int findLast(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] <= target) {left = mid + 1; // 目標值在右半部分或者當前位置就是目標值} else if (nums[mid] > target) {right = mid - 1; // 目標值在左半部分}}// 當退出循環時，right 指向最后一個小于等于目標值的位置return right; // 直接返回 right，即最后一次出現的位置
}

5.LeetCode 33 搜索旋轉排序數組

在這里插入圖片描述

解法

題目要求我們設計一個時間復雜度為O（logN）的算法，很容易就想到二分法。

但是本題整個數組并不是完全有序的，而是被“旋轉”拆分成了兩個部分。

如果我們能找到那個旋轉點的話，在兩個有序的部分進行二分查找就非常輕松了。

那么如果直接遍歷數組去找旋轉點的話，時間復雜度還是會上升到O（N），不符合題目要求。

我們能不能也用二分去尋找這個旋轉點呢？答案是可以的。

eg 4 5 6 7 1 2 3——旋轉點在 1 處
我們以arr[0]，也就是4為基準，用mid 去跟 arr[0]比較，如果mid>arr[0],說明旋轉點在mid右邊，如果mid<arr[0],那么可能當前就是旋轉點，或者旋轉點在右邊。

這也算是滿足二段性的一個例子了——二分法并不是一定要有序的時候才能用，滿足二段性時，也可以使用。


//查找旋轉點 
public static int findRotationPointIndex(int[] arr) {// 如果數組長度為2，直接返回較小元素的索引if (arr.length == 2) return arr[0] < arr[1] ? 0 : 1;// 初始化左右邊界int left = 0;int right = arr.length - 1;// 二分查找旋轉點while (left < right) {int mid = left + (right - left) / 2;if (arr[mid] >= arr[0]) {left = mid + 1;  // mid處于前半段遞增序列，旋轉點在右半段} else {right = mid;     // mid處于后半段遞增序列或是旋轉點}}return left;  // left指向旋轉點的索引
}

查找到旋轉點之后，我們再在兩端進行二分查找就比較容易了。

public int search(int[] arr, int target) {// 如果數組長度為1，直接比較目標值與數組唯一元素if (arr.length == 1) return target == arr[0] ? 0 : -1;// 找到旋轉點的索引int index = findRotationPointIndex(arr);// 初始化左右邊界int left = 0;int right = arr.length - 1;// 確定二分查找的范圍if (index == 0) {// 數組沒有旋轉，直接在整個數組上執行二分查找return binaryFind(arr, left, right, target);}if (target >= arr[0]) {right = index; // 目標值可能在旋轉點之前（包括旋轉點）} else {left = index; // 目標值在旋轉點之后}// 在確定的范圍內執行二分查找return binaryFind(arr, left, right, target);}//二分查找public static int binaryFind(int[] arr, int left, int right, int target) {while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] == target) {return mid;} else if (arr[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return -1;}

在這里插入圖片描述

6.LeetCode 475 供暖器

在這里插入圖片描述

解法

核心思路就是兩句話：
（1）對于每個房屋，要么用前面的暖氣，要么用后面的，二者取近的，得到距離；
（2）對于所有的房屋，選擇最大的上述距離。

所以我們可以將heaters排好序，然后對每個房屋利用二分法去搜索最近的（相鄰的）供暖器即可。

代碼實現：

public int findRadius(int[] houses, int[] heaters) {// 首先對加熱器的位置數組進行排序Arrays.sort(heaters);// 初始化答案為0int ans = 0;int n = houses.length;// 遍歷房屋的位置數組for (int i = 0; i < n; i++) {// 對于每個房屋位置，調用二分查找函數找到其最近的加熱器，并更新答案ans = Math.max(binarySearch(heaters, houses[i]), ans);}// 返回最大半徑return ans;}// 二分查找函數，用于找到距離目標最近的加熱器public int binarySearch(int[] nums, int target) {int n = nums.length;// 如果目標大于等于加熱器數組中最后一個加熱器的位置，直接返回目標與最后一個加熱器位置的距離差if (target >= nums[n - 1]) return target - nums[n - 1];// 如果目標小于等于加熱器數組中第一個加熱器的位置，直接返回第一個加熱器位置與目標的距離差if (target <= nums[0]) return nums[0] - target;// 初始化左右邊界int l = 0, r = n - 1;// 開始二分查找while (l <= r) {int mid = l + (r - l) / 2;if (nums[mid] == target) {return 0; // 如果找到目標位置，返回距離差為0} else if (nums[mid] < target) {l = mid + 1; // 如果目標在當前中間值的右側，更新左邊界} else {r = mid - 1; // 如果目標在當前中間值的左側，更新右邊界}}// 循環結束時，l指向的位置即為最終找到的最近的那個比他大的加熱器的位置//取兩個差值的最小值return Math.min(nums[l] - target, target - nums[l - 1]);}

7.LeetCode 287 尋找重復數

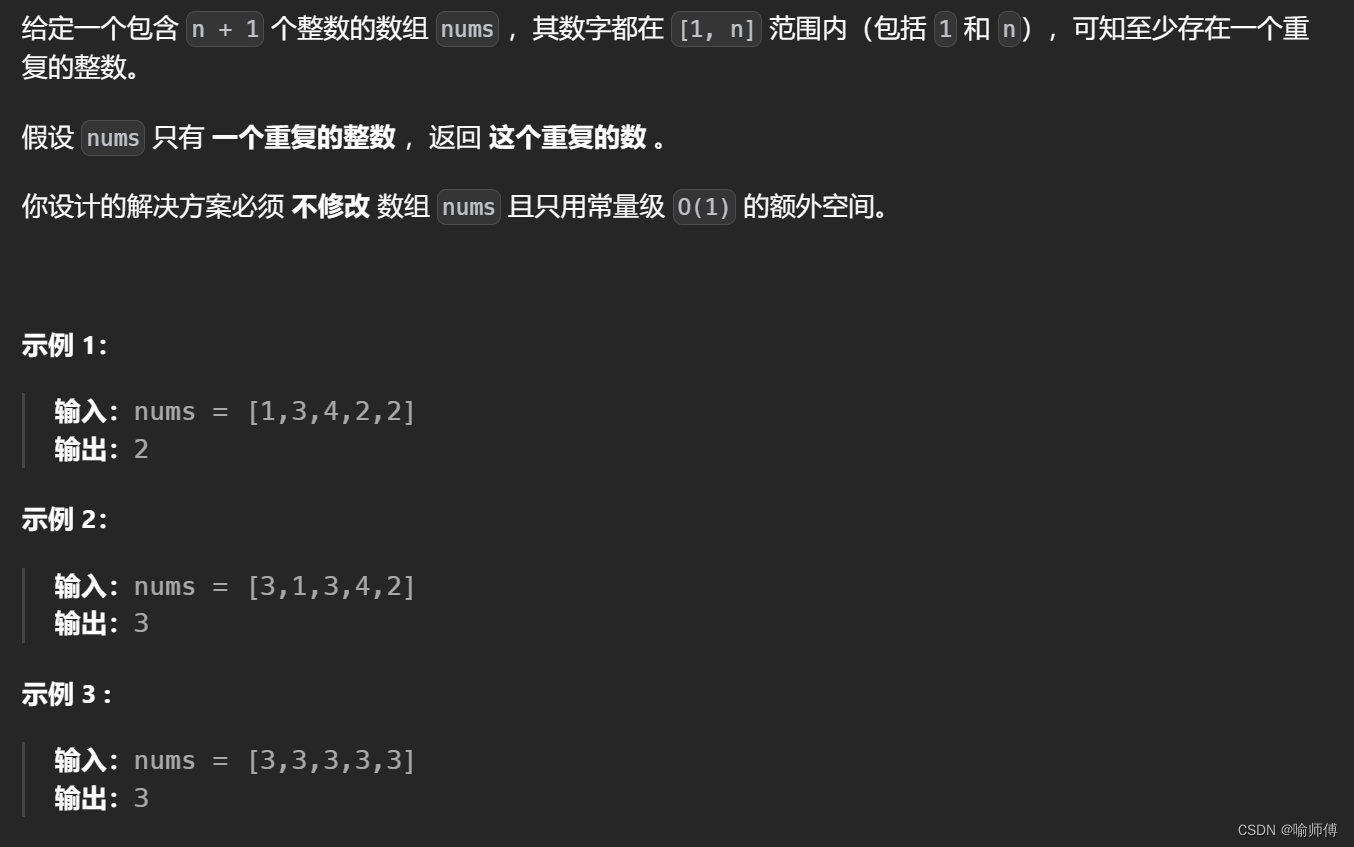
在這里插入圖片描述

這道題博主咋也想不出來能用二分法哈哈哈哈，想破腦殼也找不到二段性
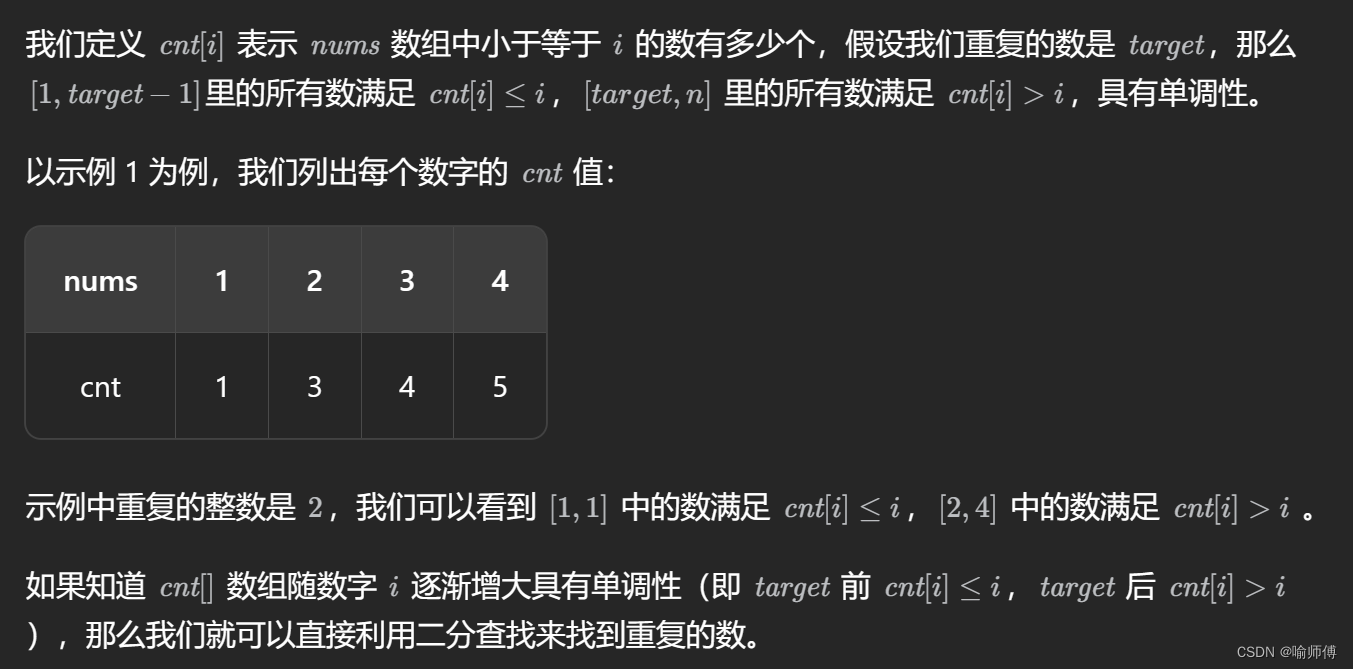
但是還有有二段性滴~ 哈哈哈哈剛開始看不太明白沒關系博主也琢磨了好一會兒差點放棄了…
自己在紙上找一些例子畫一畫慢慢就能get到這個點啦

在這里插入圖片描述

代碼實現

// 尋找重復元素的方法，輸入是一個整數數組 nums
public int findDuplicate(int[] nums) {int n = nums.length; // 數組的長度int l = 1, r = n - 1; // 設定搜索范圍，因為題目給出了1到n-1之間的數字重復，所以左邊界為1，右邊界為n-1int ans = -1; // 初始化答案為-1，因為題目保證了一定存在重復元素，因此初始值不影響結果// 開始二分搜索while (l <= r) {int mid = l + (r - l) / 2; // 計算中間值int cnt = 0; // 統計小于等于mid的元素個數for (int num : nums) {if (num <= mid) {cnt++;}}// 如果小于等于mid的元素個數(cnt)小于等于mid本身，則重復元素在[mid+1, r]范圍內if (cnt <= mid) {l = mid + 1; // 更新左邊界，縮小搜索范圍到[mid+1, r]} else {r = mid - 1; // 否則重復元素在[l, mid-1]范圍內ans = mid; // 更新答案為當前的mid，因為mid可能是重復的數字}}return ans; // 返回找到的重復元素
}