Matlab/Python:
本文KAU將介紹一個2020年發表在1區期刊ESWA上的優化算法——海洋捕食者算法 (Marine Predators Algorithm,MPA)[1]

該算法由Faramarzi等于2020年提出,其靈感來源于海洋捕食者之間不同的覓食策略、最佳相遇概率策略、海洋記憶存儲與海洋漩渦以及魚類聚集效應影響。
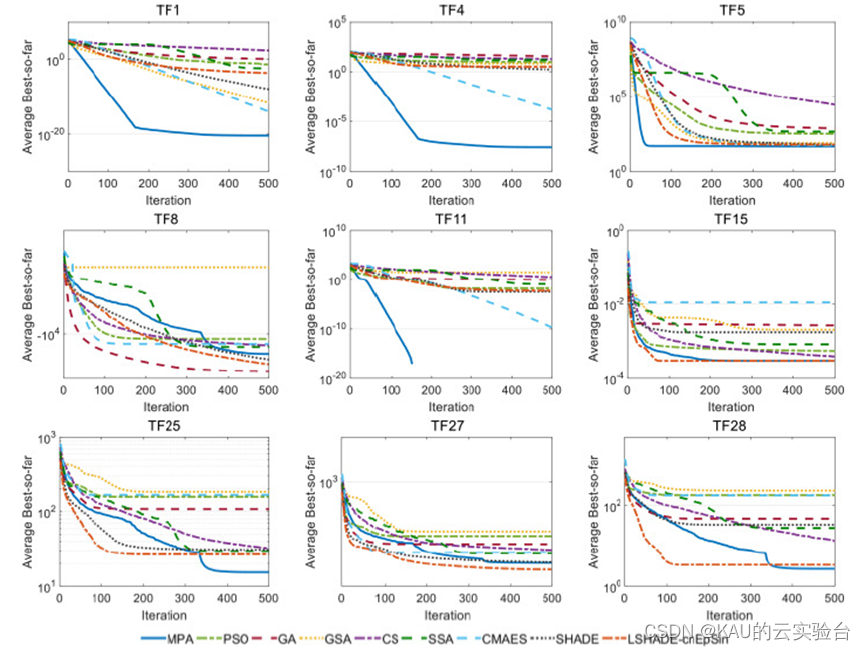
算法性能上,在通風和建筑能源性能領域的29個測試函數、CEC2017及3個工程基準和2個工程實際問題等上進行評估,對比算法包含3類:
(1)GA、PSO-研究最充分的啟發式算法;
(2)GSA、CS、SSA-最近開發的算法;
(3)CMA-ES、SHADE、LSHADE-高性能與CEC優勝算法
MPA性能排名第二!
MPA算法共分為三個階段,設計的挺有意思,如果有想做算法改進的朋友也可以看下去,本文將介紹該算法的相關原理并給出其MATLAB和Python實現。
00 目錄
1 海洋捕食者算法(MPA)原理
2 代碼目錄
3 算法性能
4 源碼獲取
01 海洋捕食者算法(MPA)原理
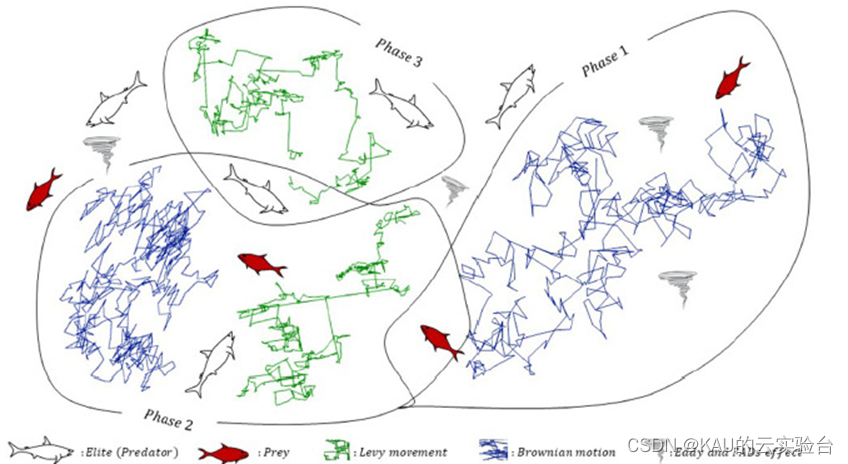
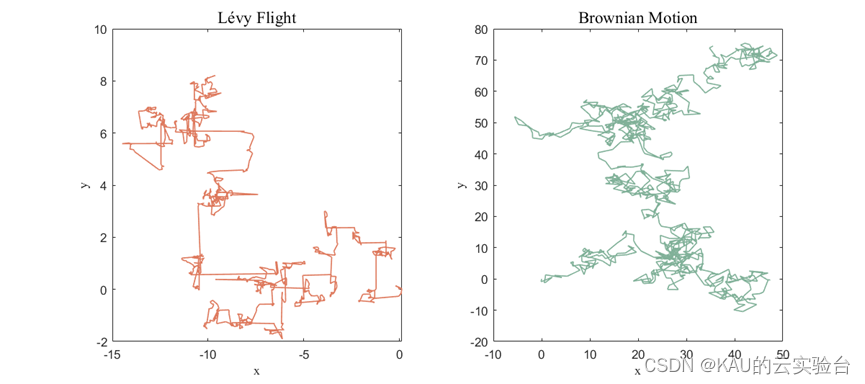
MPA算法的靈感來自海洋生物的捕食行為和捕食策略,MPA 算法中海洋生物以萊維運動(Lévy flight/walk)和布朗(Brownian)運動兩種捕食策略進行捕食。在海洋捕食者算法的優化過程中,算法針對不同的階段,通過平衡萊維運動和布朗運動增加海洋捕食者和獵物之間相遇的可能性(做算法改進時,這點可以作參考!)。
在介紹算法步驟前,KAU先介紹海洋捕食者的覓食策略,即萊維飛行與布朗運動,再對MPA的算法原理進行介紹:
1.1 布朗運動
海洋捕食者在在獵物豐富的區域使用布朗運動策略。MPA 使用的是標準布朗運動,其隨機生成的步長由零均值((u=0)和單位方差(σ2=1)的高斯分布定義的概率函數得出。在點 x 的可能概率函數:
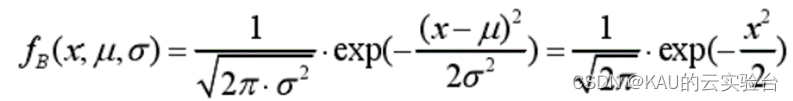
1.2 萊維飛行
海洋捕食者在獵物數量稀少的海洋環境中采用萊維飛行策略。萊維飛行本質上是一種隨機游走策略,其步長遵循萊維分布。為了生成穩定的萊維分布,通常根據 Mantegna 算法生成服從萊維分布的隨機數。步長 S 的計算方式如下:
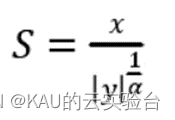
式中:α表示在0到2范圍內的指數分布,x和y是兩個正態分布變量:
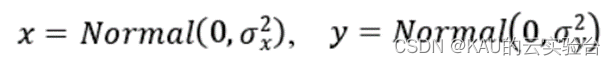
標準差σx和σy定義如下:
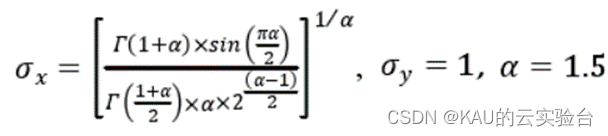
式中:Γ是伽瑪函數,整數z的函數定義為:
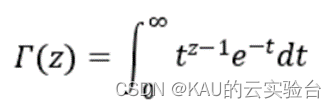
兩種分布的軌跡如下:
1.3 MPA算法步驟
海洋捕食者算法尋優主要通過三個主要階段來執行;其中,包括初始化、優化和FADs效應三個階段。
1.3.1 初始化
MPA 是一種基于種群的方法,其初始解與其他元啟發式算法一樣,均勻分布在搜索空間中:
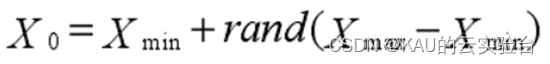
其中,Xmin和Xmax分別表示求解問題中變量的最小值和最大值,rand 表示(0,1)中的均勻隨機數。
捕食者在尋找食物時,獵物也在尋找食物,因此,需要定義兩個矩陣。選取最優解作為頂端捕食者,構造一個名為 Elite 矩陣,該矩陣數組監視搜索過程,并根據獵物的位置信息搜索獵物。第二個矩陣是 Prey 矩陣,它的維數與 Elite 相同,捕食者基于這個矩陣進行更新。在每次迭代結束時,如果出現適應度值更高的捕食者,當前頂端的捕食者會被替換,精英矩陣隨之更新。Elite 矩陣和 Prey 矩陣定義如下:
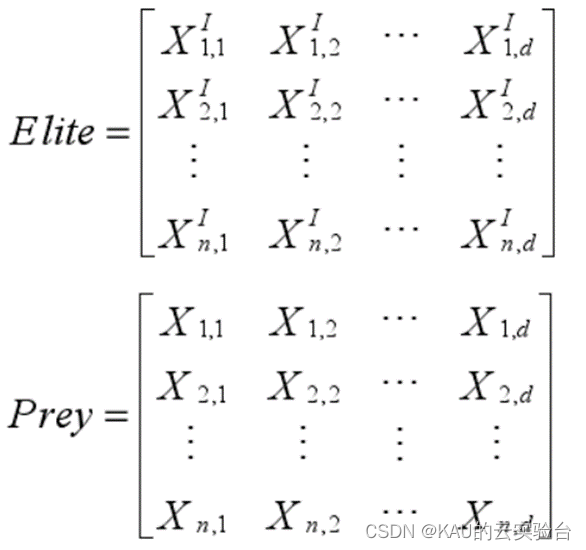
其中,n為種群數量,d為問題維度。
1.3.2 優化
MPA 考慮了捕食者和獵物的速度比例,定義了三個階段的位置更新公式。v 表示了獵物和捕食者的速度比例,并明確了三個階段及其對應的公式,每種方式都
有一個預設的迭代周期,具體如下:
階段 1:高速度比
該階段處于算法迭代次數的前三分之一,在這期間執行算法的勘探。獵物比捕食者游得更快(v>10 ),捕食者因自身速度遠低于獵物而放棄捕獵,不移動,獵物執行布朗運動,該階段數學模型為:

在公式(2.4)中,RB表示布朗運動,該向量是服從正態分布的隨機向量。RB與獵物點乘表示模擬獵物的布朗運動;P 表示一個常數通常取 P =0.5,R表示服從[0,1]均勻分布的隨機向量。 Iter為當前的迭代次數, Max_ Iter為最大迭代次數。
階段 2:相同速度比
該階段處于算法迭代次數的三分之一到三分之二,在這期間算法從勘探向開發的過渡。獵物和捕食者的速度基本相同(v≈1),此時捕食者和獵物都在尋找各自的獵物,整個種群被分為兩個部分,其中一部分代表捕食者用于勘探(布朗運動),另一部分代表獵物用于開發(萊維飛行)。該階段的數學模型可用如下公式表示:
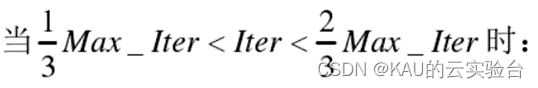
前一半種群,獵物開發:
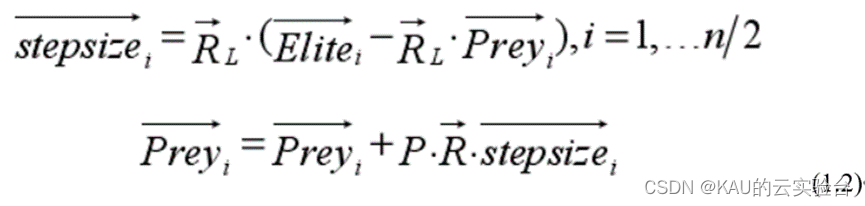
其中,RL表示模擬萊維運動的隨機數向量,通過RL 與 Prey 相乘模擬獵物進行萊維運動。
后一半種群,捕食者勘探:
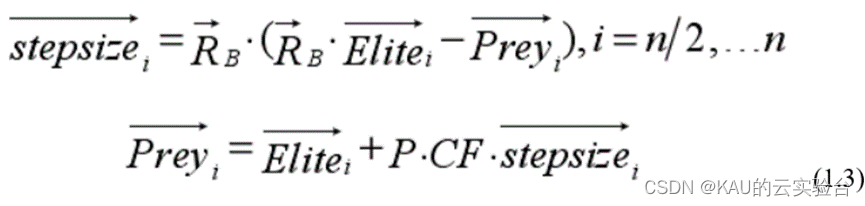
通過RB與 Elite 相乘模擬捕食者進行布朗運動,獵物根據捕食者的運動來更新自己位置,CF 是控制捕食者移動步長的自適應參數,更新公式如下.
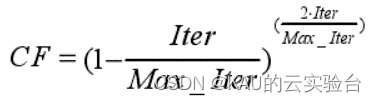
階段 3:低速度比
該階段處于算法總迭代次數的最后三分之一,主要是提高算法的開發能力。在這個時段,獵物的移動速度比捕食者慢(v=0.1),捕食者的策略是萊維運動:
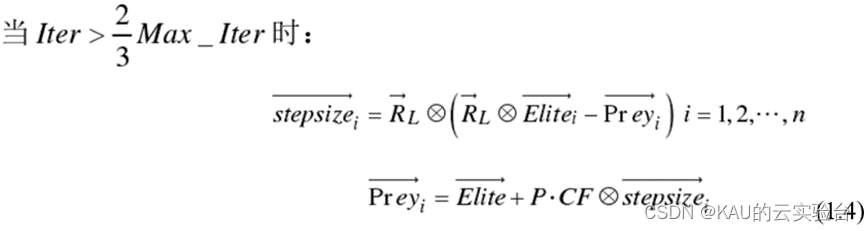
1.3.3 FADs效應
導致海洋捕食者行為改變的還有環境因素,如渦流形成或魚群聚集裝置(FADs)效應。在這些因素的影響下,它們可能需要在不同的維度上進行更長時間的跳躍,以尋找另一個獵物分布的環境。FADs 可以表示探索區域的局部最優。通過在算法優化過程中設置更長的跳躍可以避免陷入局部最優。
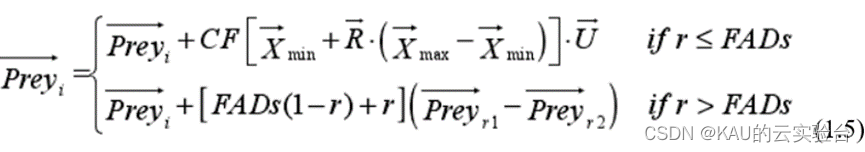
其中,FADs 表示影響算法優化過程的概率,通常情況下取 0.2;U是隨機生成的0或1的二進制向量序列;R為[0,1]之間的隨機數;r1和r2為獵物矩陣的隨機索引。當 r ≤FADs 時,捕食者會在不同的維度上進行更長時間的跳躍,以此來尋找其他最優解分布空間,從而達到跳出局部最優的效果。當 r >FADs時,捕食者會在當前的捕食者空間內隨機移動。
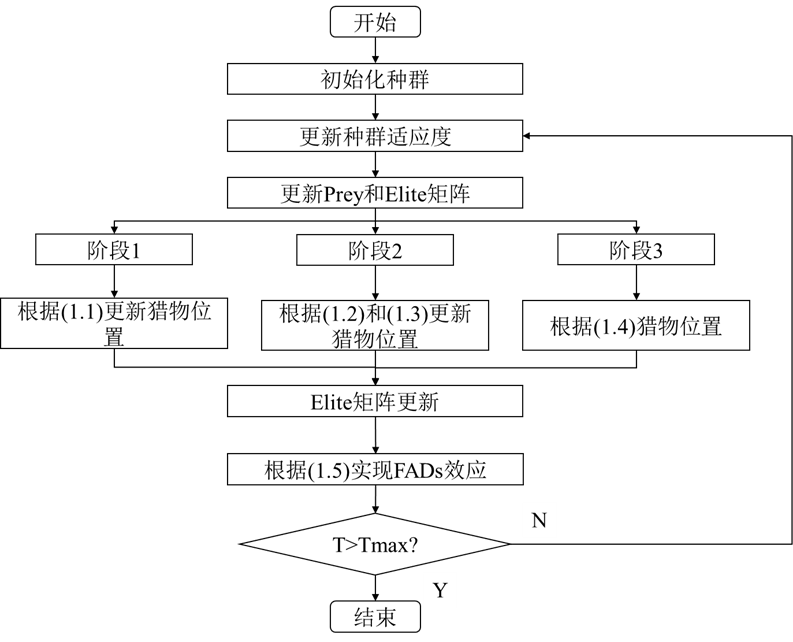
1.4 算法流程圖
MPA算法核心在于萊維飛行與布朗運動的轉換應用,其在不同階段的更新思路都可以作為算法改進的學習之處,同時,MPA算法還設計了一種跳出局部最優的策略,同樣也可作為參考。MPA算法的流程圖如下:
02 代碼目錄
包含Matlab、Python文件以及MPA算法源文獻
代碼都經過作者重新注釋,代碼更清爽,可讀性強,其中Readme給出了一些注意:

部分代碼:
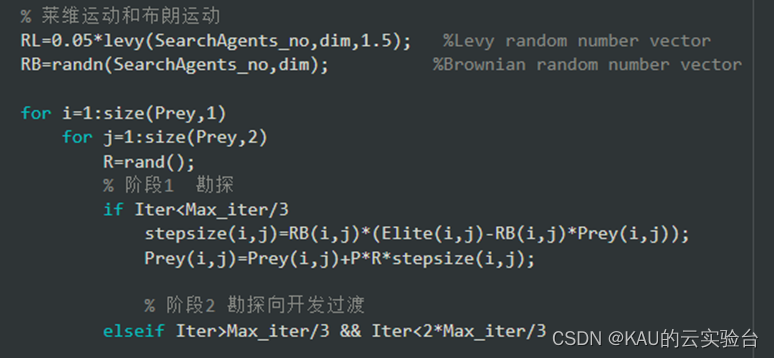
03 算法性能
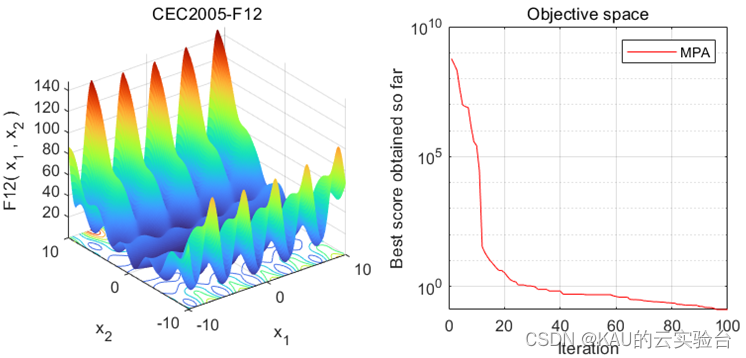
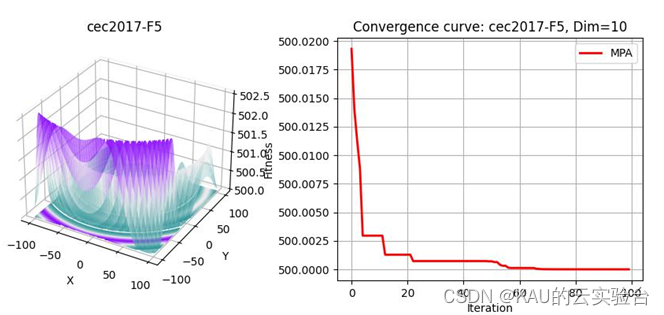
采用CEC測試函數初步檢驗其尋優性能
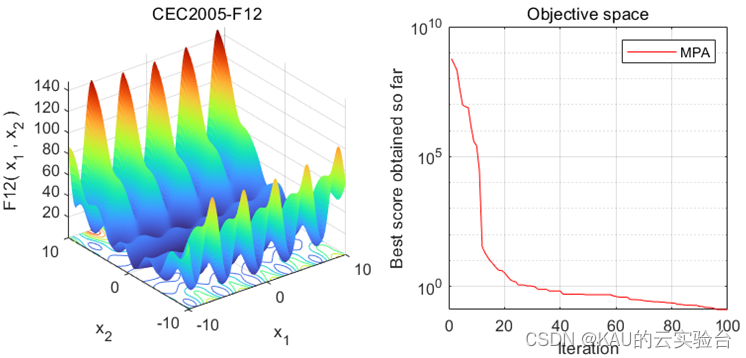
在MATLAB中,執行程序結果如下:
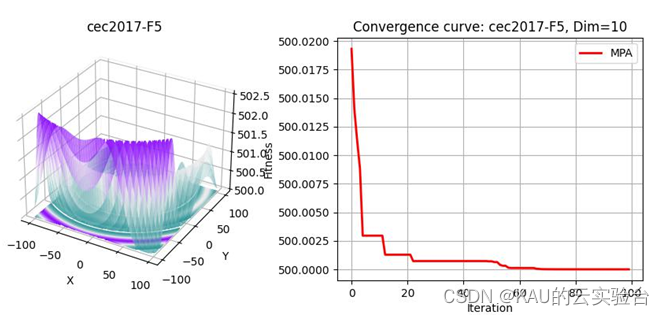
在PYTHON中,執行程序結果如下:
04 源碼獲取
在公眾號(KAU的云實驗臺)后臺回復 MPA 即可~?
參考文獻
[1] FARAMARZI A,HEIDARINEJAD M,MIRJALILI S,et al.Marine predators algorithm:a nature-inspired metaheuristic[J].Expert Systems with Applications,2020,152:113377.
另:如果有伙伴有待解決的優化問題(各種領域都可),可以發我,我會選擇性的更新利用優化算法解決這些問題的文章。
如果這篇文章對你有幫助或啟發,可以點擊右下角的贊/在看(? ??_??)?(不點也行),你們的鼓勵就是我堅持的動力!若有定制需求,可私信作者。





:循環群的兩道例題)







)




【獨一無二】)
