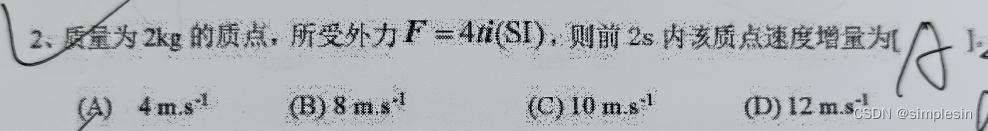
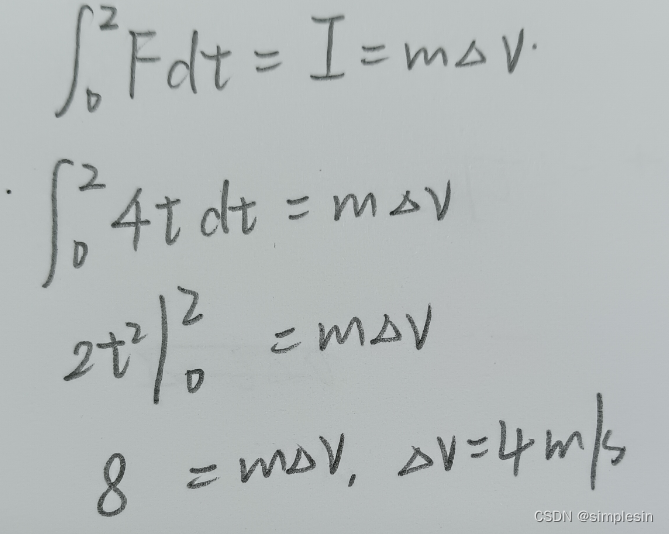
平衡位置：在O點上的位置?
相位：
?
當N很大的時候，wx=wy=wz。因此，平均平動動能除以3，就是能量均分定理。
W= F在x上的積分
Π時無單位
180°，°就是單位
1rad，rad就是單位
左手定則、右手定則、安培定則、右手螺旋定則全搞定！_嗶哩嗶哩_bilibili?
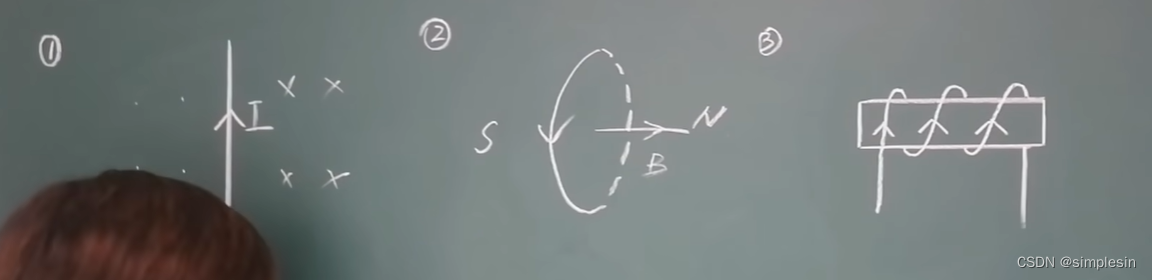
右手：拇指指向電流方向，四指是環繞方向，是判斷磁場方向的
?
均勻帶電圓環，半徑為R 電量為Q，真空的電容率為c，選無窮遠處為電勢零參考點，則環心處的電勢為
均勻帶電圓環的對環心處的電勢可以等效為什么?
均勻帶電圓環對環心處的電勢可以等效為一個位于環心、電量等于圓環總電量的點電荷所產生的電勢。這是因為在環心這樣一個特殊位置，圓環上所有電荷產生的電場在環心處的合成效應對稱地相互抵消，除了沿徑向的分量，但由于環心位于環的中心，徑向電場分量也在各個方向上完全對稱并互相抵消，最終導致環心處的實際電場為零。然而，電勢是標量，它累積了所有電荷的貢獻而不受方向影響。
因此，盡管環心處的電場為零，環心處的電勢卻不為零，且可以視作環上所有電荷“集中”在環心這一點上時產生的電勢。這意味著，計算環心電勢時，可以將整個圓環看作全部電量 Q?集中在環心的一個點電荷，然后使用點電荷電勢的公式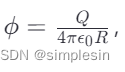
,其中 R是從假設的點電荷位置（即環心）到考察點的距離，在這種情況下也就是圓環的半徑。
所以，均勻帶電圓環對環心的電勢等效于一個電量為 Q、位于環心的點電荷產生的電勢。
容器內液體作用在容器底部的壓力一定等于液體的重力嗎
容器內液體作用在容器底部的壓力不一定總是等于液體的重力。這個壓力的大小取決于幾個因素，主要是容器的形狀和液體的高度：
-
柱形容器：如果液體存儲在一個上下直徑一致的柱形容器中（例如圓柱體或長方體，且頂部開口），在這種對稱且均勻的條件下，液體對容器底部的壓力確實是等于液體的重力。這是因為在這樣的容器中，液體的重力完全轉化為對底部的垂直壓力，沒有側壁或其他因素分散這部分力。
-
非柱形容器：對于形狀不規則的容器，比如上寬下窄或上窄下寬的容器，情況就不同了。在上寬下窄（如漏斗形）的容器中，液體對底部的壓力會小于液體的重力，因為部分壓力被側壁承擔了，通過側壁傳遞到了容器的其他支撐部分。而在上窄下寬的容器中，所有液體的重力都直接或間接地作用到底部，此時底部壓力可能大于僅考慮液體自重的情況，因為還包含了容器壁對液體的反作用力分量。
-
容器傾斜或有特殊設計：如果容器傾斜放置或有特殊的結構設計（如帶弧度的底部或有坡度），液體對底部的壓力也會受到這些因素的影響，可能并不直接等于液體的重力。
總結來說，液體對容器底部的壓力是否等于液體的重力，需要具體分析容器的幾何形狀和液體的分布情況。在大多數非特殊設計的容器中，尤其是當容器底部直接承載液體且無特殊流體力學效應時，壓力和重力之間的關系較為直接；而在設計復雜或具有特定幾何特性的容器中，則需更細致的力學分析。
