【sklearn】【邏輯回歸1】

學習筆記來自：

所用的庫和版本大家參考：

Python 3.7.1
Scikit-learn 0.20.1?
Numpy 1.15.4, Pandas 0.23.4, Matplotlib 3.0.2, SciPy 1.1.0

1 概述

1.1 名為“回歸”的分類器

在過去的四周中，我們接觸了不少帶“回歸”二字的算法，回歸樹，隨機森林的回歸，無一例外他們都是區別于分類算法們，用來處理和預測連續型標簽的算法。然而邏輯回歸，是一種名為“回歸”的線性分類器，其本質是由線性回歸變化而來的，一種廣泛使用于分類問題中的廣義回歸算法。要理解邏輯回歸從何而來，得要先理解線性回歸。線性回歸是機器學習中最簡單的的回歸算法，它寫作一個幾乎人人熟悉的方程：

通過函數z，線性回歸使用輸入的特征矩陣X來輸出一組連續型的標簽值y_pred，以完成各種預測連續型變量的任務 (比如預測產品銷量，預測股價等等)。那如果我們的標簽是離散型變量，尤其是，如果是滿足0-1分布的離散型變量，我們要怎么辦呢?我們可以通過引入聯系函數(link function)，將線性回歸方程z變換為g(z)，并且令g(z)的值分布在(0,1)之間，且當g(z)接近0時樣本的標簽為類別0，當g(z)接近1時樣本的標簽為類別1，這樣就得到了一個分類模型。而這個聯系函數對于邏輯回歸來說，就是Sigmoid函數:

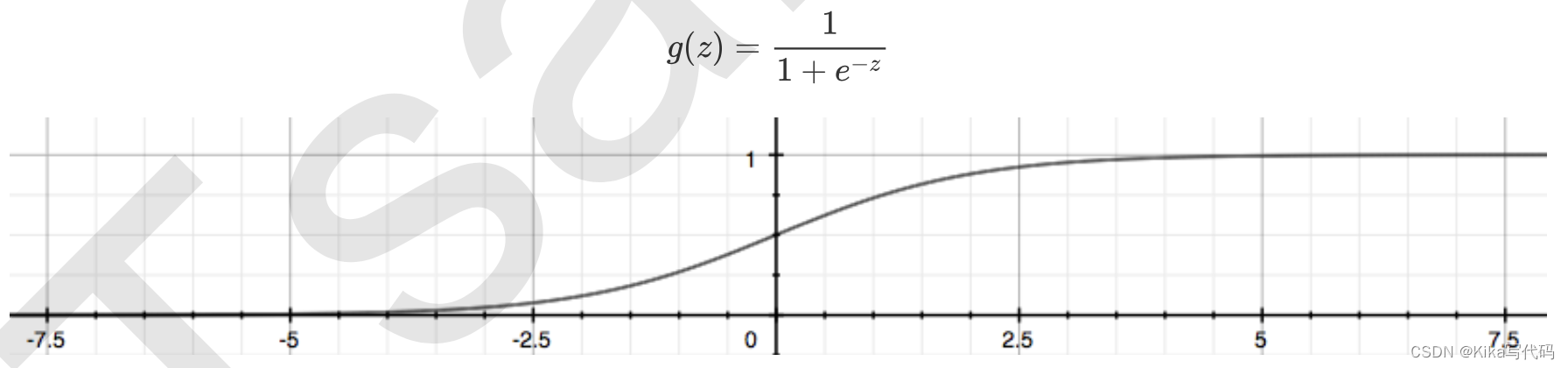
面試高危問題：Sigmoid函數的公式和性質

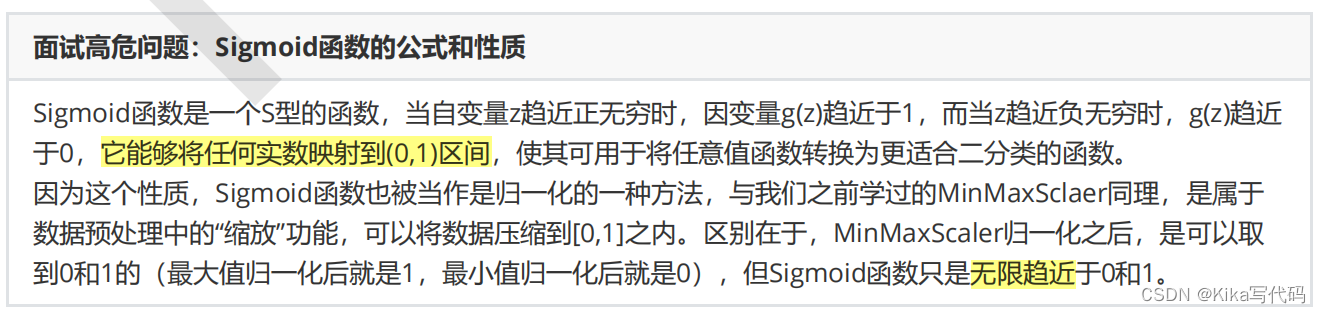
不難發現，g(z)的形似幾率取對數的本質其實就是我們的線性回歸z，我們實際上是在對線性回歸模型的預測結果取對數幾率來讓其的結果無限逼近0和1。因此，其對應的模型被稱為”對數幾率回歸“(logistic Regression)，也就是我們的邏輯回歸，這個名為“回歸”卻是用來做分類工作的分類器。

思考：g(z)代表了樣本為某一類標簽的概率嗎？

1.2 為什么需要邏輯回歸

線性回歸對數據的要求很嚴格，比如標簽必須滿足正態分布，特征之間的多重共線性需要消除等等，而現實中很多真實情景的數據無法滿足這些要求，因此線性回歸在很多現實情境的應用效果有限。邏輯回歸是由線性回歸變化而來，因此它對數據也有一些要求，而我們之前已經學過了強大的分類模型決策樹和隨機森林，它們的分類效力很強，并且不需要對數據做任何預處理。

何況，邏輯回歸的原理其實并不簡單。一個人要理解邏輯回歸，必須要有一定的數學基礎，必須理解損失函數，正則化，梯度下降，海森矩陣等等這些復雜的概念，才能夠對邏輯回歸進行調優。其涉及到的數學理念，不比支持向量機少多少。況且，要計算概率，樸素貝葉斯可以計算出真正意義上的概率，要進行分類，機器學習中能夠完成二分類功能的模型簡直多如牛毛。因此，在數據挖掘，人工智能所涉及到的醫療，教育，人臉識別，語音識別這些領域，邏輯回歸沒有太多的出場機會。

甚至，在我們的各種機器學習經典書目中，周志華的《機器學習》400頁僅有一頁紙是關于邏輯回歸的(還是一頁數學公式)，《數據挖掘導論》和《Python數據科學手冊》中完全沒有邏輯回歸相關的內容，sklearn中對比各種分類器的效應也不帶邏輯回歸玩，可見業界地位。

但是，無論機器學習領域如何折騰，邏輯回歸依然是一個受工業商業熱愛，使用廣泛的模型，因為它有著不可替代的優點:

邏輯回歸對線性關系的擬合效果好到喪心病狂，特征與標簽之間的線性關系極強的數據，比如金融領域中的信用卡欺詐，評分卡制作，電商中的營銷預測等等相關的數據，都是邏輯回歸的強項。雖然現在有了梯度提升樹GDBT，比邏輯回歸效果更好，也被許多數據咨詢公司啟用，但邏輯回歸在金融領域，尤其是銀行業中的統治地位依然不可動搖(相對的，邏輯回歸在非線性數據的效果很多時候比瞎猜還不如，所以如果你已經知道數據之間的聯系是非線性的，千萬不要迷信邏輯回歸)
邏輯回歸計算快:對于線性數據，邏輯回歸的擬合和計算都非常快，計算效率優于SVM和隨機森林，親測表示在大型數據上尤其能夠看得出區別
邏輯回歸返回的分類結果不是固定的0，1，而是以小數形式呈現的類概率數字:我們因此可以把邏輯回歸返回的結果當成連續型數據來利用。比如在評分卡制作時，我們不僅需要判斷客戶是否會違約，還需要給出確定的”信用分“，而這個信用分的計算就需要使用類概率計算出的對數幾率，而決策樹和隨機森林這樣的分類器，可以產出分類結果，卻無法幫助我們計算分數(當然，在sklearn中，決策樹也可以產生概率，使用接口predict_proba調用就好，但一般來說，正常的決策樹沒有這個功能)。

另外，邏輯回歸還有抗噪能力強的優點。福布斯雜志在討論邏輯回歸的優點時，甚至有著“技術上來說，最佳模型的AUC面積低于0.8時，邏輯回歸非常明顯優于樹模型”的說法。并且，邏輯回歸在小數據集上表現更好，在大型的數據集上，樹模型有著更好的表現。

由此，我們已經了解了邏輯回歸的本質，它是一個返回對數幾率的，在線性數據上表現優異的分類器，它主要被應用在金融領域。其數學目的是求解能夠讓模型最優化的參數的值，并基于參數和特征矩陣計算出邏輯回歸的結果 y(x)。注意:雖然我們熟悉的邏輯回歸通常被用于處理二分類問題，但邏輯回歸也可以做多分類。

1.3 sklearn中的邏輯回歸

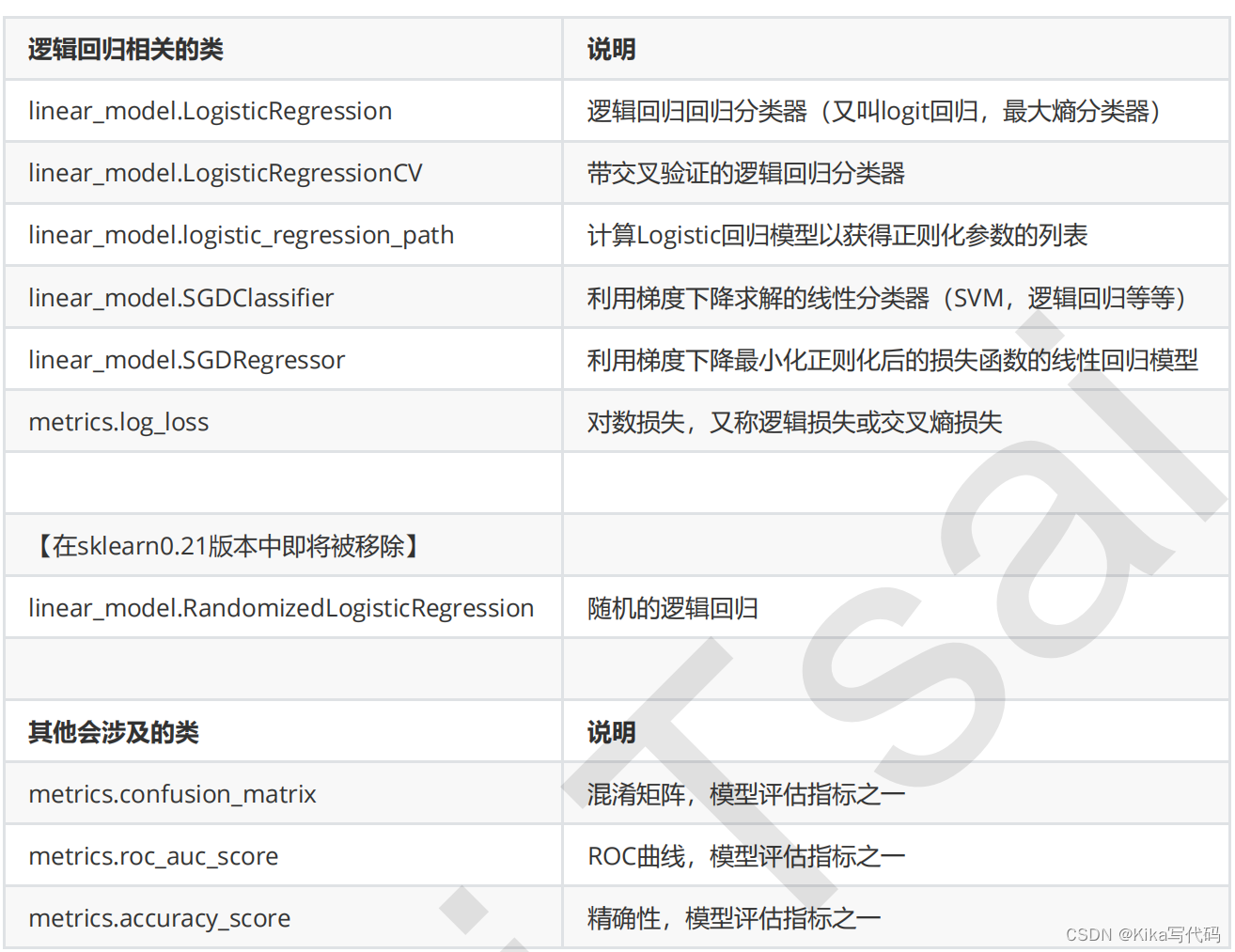
2 linear_model.LogisticRegression

?2.1 二元邏輯回歸的損失函數

在學習決策樹和隨機森林時，我們曾經提到過兩種模型表現:在訓練集上的表現，和在測試集上的表現。我們建模，是追求模型在測試集上的表現最優，因此模型的評估指標往往是用來衡量模型在測試集上的表現的。然而，邏輯回歸有著基于訓練數據求解參數 $\theta$ 的需求，并且希望訓練出來的模型能夠盡可能地擬合訓練數據，即模型在訓練集上的預測準確率越靠近100%越好。

因此，我們使用”損失函數“這個評估指標，來衡量參數 $\theta$ 的優劣，即這一組參數能否使模型在訓練集上表現優異。如果用一組參數建模后，模型在訓練集上表現良好，那我們就說模型表現的規律與訓練集數據的規律一致，擬合過程中的損失很小，損失函數的值很小，這一組參數就優秀；相反，如果模型在訓練集上表現糟糕，損失函數就會很大，模型就訓練不足，效果較差，這一組參數也就比較差。即是說，我們在求解參數 $\theta$ 時，追求損失函數最小，讓模型在訓練數據上的擬合效果最優，即預測準確率盡量靠近100%。

關鍵概念：損失函數

邏輯回歸的損失函數是由最大似然法來推導出來的，具體結果可以寫作:

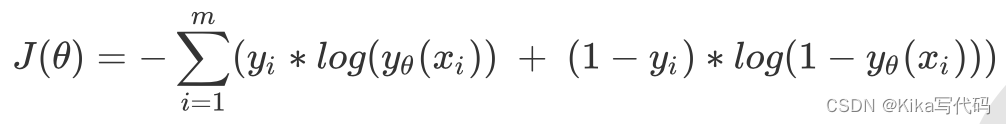
由于我們追求損失函數的最小值，讓模型在訓練集上表現最優，可能會引發另一個問題:

如果模型在訓練集上表示優秀，卻在測試集上表現糟糕，模型就會過擬合。雖然邏輯回歸和線性回歸是天生欠擬合的模型，但我們還是需要控制過擬合的技術來幫助我們調整模型，對邏輯回歸中過擬合的控制，通過正則化來實現。

2.2 正則化：重要參數penalty & C

正則化是用來防止模型過擬合的過程，常用的有L1正則化和L2正則化兩種選項，分別通過在損失函數后加上參數向量 $\theta$ 的L1范式和L2范式的倍數來實現。這個增加的范式，被稱為“正則項”，也被稱為"懲罰項"。

損失函數改變，基于損失函數的最優化來求解的參數取值必然改變，我們以此來調節模型擬合的程度。其中L1范數表現為參數向量中的每個參數的絕對值之和，L2范數表現為參數向量中的每個參數的平方和的開方值。

L1正則化和L2正則化雖然都可以控制過擬合，但它們的效果并不相同。當正則化強度逐漸增大（即C逐漸變小），參數 $\theta$ 的取值會逐漸變小，但L1正則化會將參數壓縮為0，L2正則化只會讓參數盡量小，不會取到0。

在L1正則化在逐漸加強的過程中，攜帶信息量小的、對模型貢獻不大的特征的參數，會比攜帶大量信息的、對模型有巨大貢獻的特征的參數更快地變成0，所以L1正則化本質是一個特征選擇的過程，掌管了參數的“稀疏性”。L1正則化越強，參數向量中就越多的參數為0，參數就越稀疏，選出來的特征就越少，以此來防止過擬合。因此，如果特征量很大，數據維度很高，我們會傾向于使用L1正則化。由于L1正則化的這個性質，邏輯回歸的特征選擇可以由Embedded嵌入法來完成。

相對的，L2正則化在加強的過程中，會盡量讓每個特征對模型都有一些小的貢獻，但攜帶信息少，對模型貢獻不大的特征的參數會非常接近于0。通常來說，如果我們的主要目的只是為了防止過擬合，選擇L2正則化就足夠了。但是如果選擇L2正則化后還是過擬合，模型在未知數據集上的效果表現很差，就可以考慮L1正則化。

而兩種正則化下C的取值，都可以通過學習曲線來進行調整。

建立兩個邏輯回歸，L1正則化和L2正則化的差別就一目了然了：

from sklearn.linear_model import LogisticRegression as LR 
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split 
from sklearn.metrics import accuracy_scoredata = load_breast_cancer() 
X = data.data
y = data.targetdata.data.shapelrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000) 
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000)#邏輯回歸的重要屬性coef_，查看每個特征所對應的參數 
lrl1 = lrl1.fit(X,y)
lrl1.coef_(lrl1.coef_ != 0).sum(axis=1)lrl2 = lrl2.fit(X,y) 
lrl2.coef_

可以看見，當我們選擇L1正則化的時候，許多特征的參數都被設置為了0，這些特征在真正建模的時候，就不會出現在我們的模型當中了，而L2正則化則是對所有的特征都給出了參數。

究竟哪個正則化的效果更好呢?還是都差不多?

l1 = []
l2 = []
l1test = []
l2test = []Xtrain, Xtest, Ytrain, Ytest =train_test_split(X,y,test_size=0.3,random_state=420)for i in np.linspace(0.05,1,19):lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000) lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)lrl1 = lrl1.fit(Xtrain,Ytrain) 	l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain)) l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))lrl2 = lrl2.fit(Xtrain,Ytrain) l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain)) 	l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]plt.figure(figsize=(6,6)) 
for i in range(len(graph)):plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i]) 
plt.legend(loc=4) #圖例的位置在哪里?4表示，右下角
plt.show()

可見，至少在我們的乳腺癌數據集下，兩種正則化的結果區別不大。但隨著C的逐漸變大，正則化的強度越來越小，模型在訓練集和測試集上的表現都呈上升趨勢，直到C=0.8左右，訓練集上的表現依然在走高，但模型在未知數據集上的表現開始下跌，這時候就是出現了過擬合。我們可以認為，C設定為0.9會比較好。在實際使用時，基本就默認使用l2正則化，如果感覺到模型的效果不好，那就換L1試試看。

2.2 梯度下降：重要參數max_iter

之前提到過，邏輯回歸的數學目的是求解能夠讓模型最優化的參數 $\theta$ 的值，即求解能夠讓損失函數最小化的 $\theta$ 的值，而這個求解過程，對于二元邏輯回歸來說，有多種方法可以選擇，最常見的有梯度下降法(Gradient Descent)，坐標軸下降法(Coordinate Descent)，牛頓法(Newton-Raphson method)等，每種方法都涉及復雜的數學原理，但這些計算在執行的任務其實是類似的。

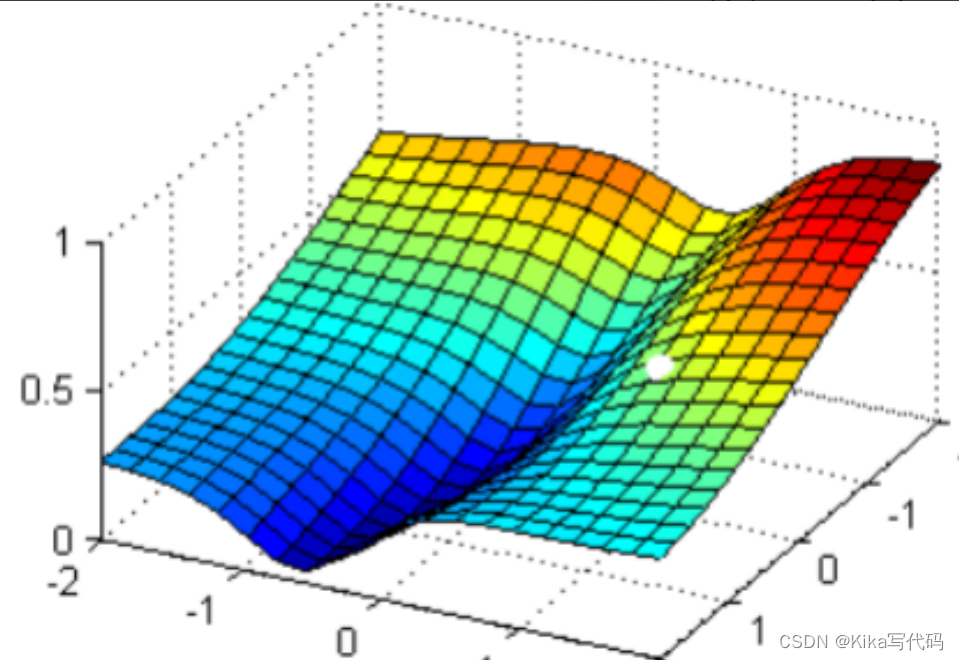
現在，我在這個圖像上隨機放一個小球，當我松手，這個小球就會順著這個華麗的平面滾落，直到滾到深藍色的區域——損失函數的最低點。但是，小球不能夠一次性滾動到最低處，它的能量不足，所以每次最多只能走距離G。為了嚴格監控這個小球的行為，我要求小球每次只能走0.05 * G，并且我要記下它每次走動的方向，直到它滾到圖像上的最低點。

現在我松手，來看小球如何運動:

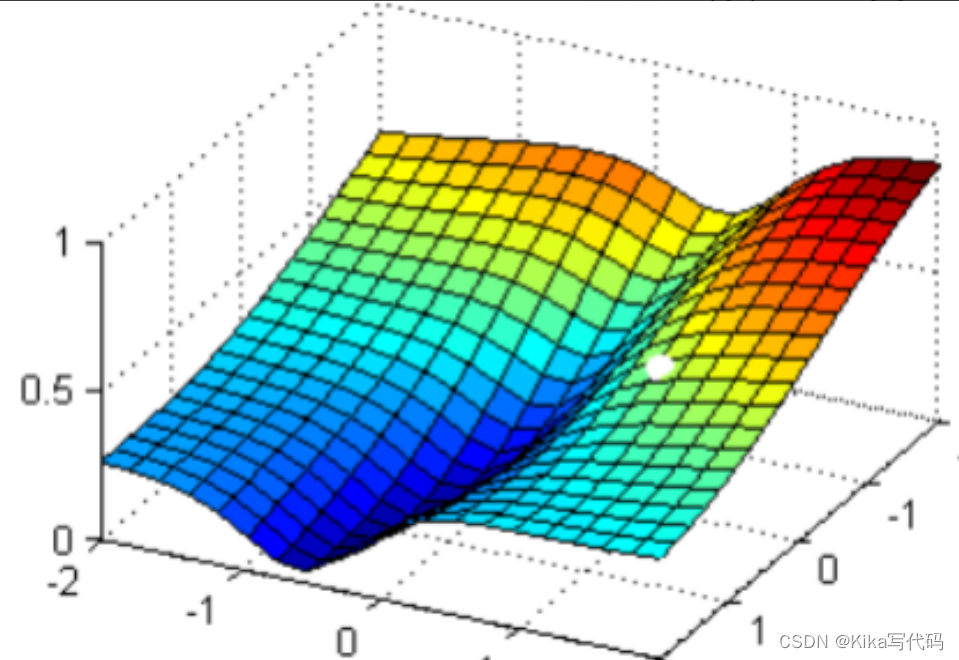
可以看見，小球從高處滑落，最終停在深藍色的區域中的某個點上，而這個點就是我們在現有狀況下可以獲得的圖像的最低點。有了這個圖像的最低點的數值，我們就可以計算出這個點所對應的參數向量 $\theta$ 了。

2.3 二元回歸與多元回歸：重要參數solver & multi_class

之前我們對邏輯回歸的討論，都是針對二分類的邏輯回歸展開，其實sklearn提供了多種可以使用邏輯回歸處理多分類問題的選項。比如說，我們可以把某種分類類型都看作1，其余的分類類型都為0值，和"數據預處理"中的二值化的思維類似，這種方法被稱為"一對多"(One-vs-rest)，簡稱OvR，在sklearn中表示為"ovr"。又或者，我們可以把好幾個分類類型劃為1，剩下的幾個分類類型劃為O值，這是一種"多對多"(Many-vs-Many)的方法，簡稱MvM，在sklearn中表示為"Multinominal"。每種方式都配合L1或L2正則項來使用。

在sklearn中，我們使用參數multi_class來告訴模型，我們的預測標簽是什么樣的類型。

multi_class

輸入"ovr " , "multinomial", "auto"來告知模型，我們要處理的分類問題的類型。默認是"ovr"。

'ovr':表示分類問題是二分類，或讓模型使用"一對多"的形式來處理多分類問題。

'multinomial':表示處理多分類問題，這種輸入在參數solver是'liblinear'時不可用。

"auto":表示會根據數據的分類情況和其他參數來確定模型要處理的分類問題的類型。比如說，如果數據是二分類，或者solver的取值為"liblinear"，"auto"會默認選擇"ovr"。反之，則會選擇"nultinomial"。

注意:默認值將在0.22版本中從"ovr"更改為"auto"。

我們之前提到的梯度下降法，只是求解邏輯回歸參數 $\theta$ 的一種方法，并且我們只講解了求解二分類變量的參數時的各種原理。sklearn為我們提供了多種選擇，讓我們可以使用不同的求解器來計算邏輯回歸。求解器的選擇，由參數"solver"控制，共有五種選擇。其中“liblinear”是二分類專用，也是現在的默認求解器。

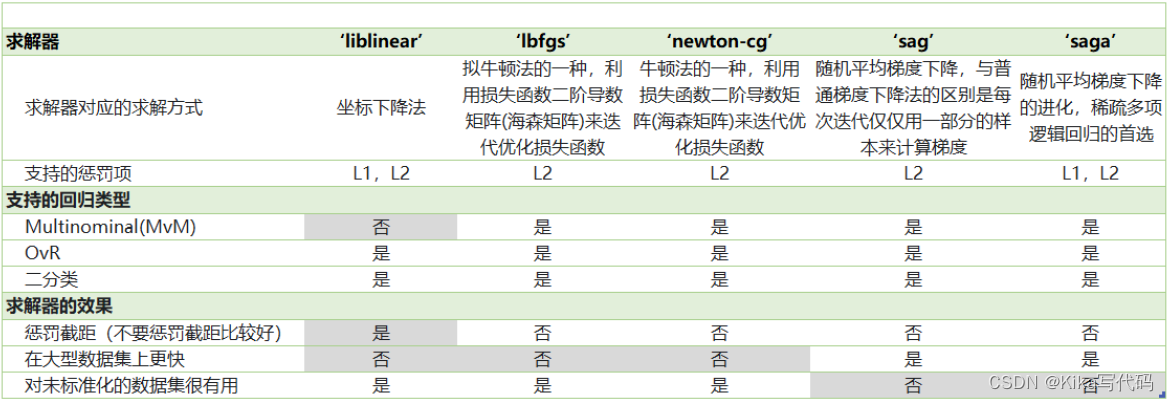
2.4 邏輯回歸中的特征選擇

當特征的數量很多的時候，我們出于業務考慮，也出于計算量的考慮，希望對邏輯回歸進行特征選擇來降維。比如，在判斷一個人是否會患乳腺癌的時候，醫生如果看5~8個指標來確診，會比需要看30個指標來確診容易得多。

業務選擇

說到降維和特征選擇，首先要想到的是利用自己的業務能力進行選擇，肉眼可見明顯和標簽有關的特征就是需要留下的。當然，如果我們并不了解業務，或者有成千上萬的特征，那我們也可以使用算法來幫助我們。或者，可以讓算法先幫助我們篩選過一遍特征，然后在少量的特征中，我們再根據業務常識來選擇更少量的特征。

PCA和SVD一般不用

說到降維，我們首先想到的是之前提過的高效降維算法，PCA和SVD，遺憾的是，這兩種方法大多數時候不適用于邏輯回歸。邏輯回歸是由線性回歸演變而來，線性回歸的一個核心目的是通過求解參數來探究特征X與標簽y之間的關系，而邏輯回歸也傳承了這個性質，我們常常希望通過邏輯回歸的結果，來判斷什么樣的特征與分類結果相關，因此我們希望保留特征的原貌。PCA和SVD的降維結果是不可解釋的，因此一旦降維后，我們就無法解釋特征和標簽之間的關系了。當然，在不需要探究特征與標簽之間關系的線性數據上，降維算法PCA和SVD也是可以使用的。

統計方法可以使用，但不是非常必要?

既然降維算法不能使用，我們要用的就是特征選擇方法。邏輯回歸對數據的要求低于線性回歸，由于我們不是使用最小二乘法來求解，所以邏輯回歸對數據的總體分布和方差沒有要求，也不需要排除特征之間的共線性，但如果我們確實希望使用一些統計方法，比如方差，卡方，互信息等方法來做特征選擇，也并沒有問題。過濾法中所有的方法，都可以用在邏輯回歸上。

在一些博客中有這樣的觀點：多重共線性會影響線性模型的效果。對于線性回歸來說，多重共線性會影響比較大，所以我們需要使用方差過濾和方差膨脹因子VIF(variance inflation factor)來消除共線性。但是對于邏輯回歸，其實不是非常必要，甚至有時候，我們還需要多一些相互關聯的特征來增強模型的表現。當然，如果我們無法通過其他方式提升模型表現，并且你感覺到模型中的共線性影響了模型效果，那懂得統計學的你可以試試看用VIF消除共線性的方法，遺憾的是現在sklearn中并沒有提供VIF的功能。

輕松一刻：R vs Python，統計學 vs 機器學習

統計學的思路是一種“先驗”的思路，不管做什么都要先”檢驗“，先”滿足條件“，事后也要各種”檢驗“，以確保各種數學假設被滿足，不然的話，理論上就無法得出好結果。而機器學習是一種”后驗“的思路，不管三七二十一，先讓模型跑一跑，效果不好再想辦法，如果模型效果好，不在意什么共線性，殘差不滿足正態分布，沒有啞變量之類的細節，模型效果好大過天！

高效的嵌入法embedded

但是更有效的方法，毫無疑問會是我們的embedded嵌入法。我們已經說明了，由于L1正則化會使得部分特征對應的參數為0，因此L1正則化可以用來做特征選擇，結合嵌入法的模塊SelectFromModel，我們可以很容易就篩選出讓模型十分高效的特征。注意，此時我們的目的是，盡量保留原數據上的信息，讓模型在降維后的數據上的擬合效果保持優秀，因此我們不考慮訓練集測試集的問題，把所有的數據都放入模型進行降維。

#導庫
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModeldata = load_breast_cancer()  # 乳腺癌數據的實例化
data.data.shapeLR_ = LR(solver=“liblinear”,C=0.8,random_state=420)
cross_val_score(LR_,data.data,data.target,cv=10).mean()#對數據進行降維
# 參數threshold(相當于特征重要性閾值)
# 參數norm_order選擇范式L1還是L2
# norm_order=1說明使用的是L1范式，模型會刪除在L1范式下面無效的特征
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
X_embedded.shapedata.target.shapecross_val_score(LR_,X_embedded,data.target,cv=10).mean()

看看結果，特征數量被減小到個位數，并且模型的效果卻沒有下降太多，如果我們要求不高，在這里其實就可以停下了。但是，能否讓模型的擬合效果更好呢？在這里，我們有兩種調整方式：

1)調節SelectFromModel這個類中的參數threshold
這是嵌入法的閾值，表示刪除所有參數的絕對值低于這個閾值的特征。現在threshold默認為None，所以SelectFromModel只根據L1正則化的結果來選擇了特征，即選擇了所有L1正則化后參數不為0的特征。我們此時，只要調整threshold的值（畫出threshold的學習曲線），就可以觀察不同的threshold下模型的效果如何變化。

一旦調整threshold，就不是在使用L1正則化選擇特征，而是使用模型的屬性.coef_中生成的各個特征的系數來選擇。coef_雖然返回的是特征的系數，但是系數的大小和決策樹中的feature_importances_以及降維算法中的可解釋性方差explained_vairance_概念相似，其實都是衡量特征的重要程度和貢獻度的，因此SelectFromModel中的參數threshold可以設置為coef_的閾值，即可以剔除系數小于threshold中輸入的數字的所有特征。

然而，這種方法其實是比較無效的，大家可以用學習曲線來跑一跑：當threshold越來越大，被刪除的特征越來越多，模型的效果也越來越差，模型效果最好的情況下需要保證有17個以上的特征。實際上我畫了細化的學習曲線，如果要保證模型的效果比降維前更好，我們需要保留25個特征，這對于現實情況來說，是一種無效的降維：需要30個指標來判斷病情，和需要25個指標來判斷病情，對醫生來說區別不大。

2)調邏輯回歸的類LR_，通過畫C的學習曲線來實現（好用！）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression as LR  # 邏輯回歸
from sklearn.model_selection import cross_val_score  # 交叉驗證
from sklearn.datasets import load_breast_cancer  # 乳腺癌數據集
from sklearn.feature_selection import SelectFromModel  # 嵌入法特征選擇data = load_breast_cancer()x = data.data
y = data.targetLR_ = LR(solver='liblinear', C=0.2, random_state=500)
print(cross_val_score(LR_, x, y, cv=10).mean())fullx = []
fsx = []c = np.arange(0.01, 10.01, 0.5)for i in c:LR_ = LR(solver='liblinear', C=i, random_state=500)# 使用沒用嵌入法降維的xfullx.append(cross_val_score(LR_, x, y, cv=10).mean())# 使用嵌入法降維x_embedded = SelectFromModel(LR_, norm_order=1).fit_transform(x, y)fsx.append(cross_val_score(LR_, x_embedded, y, cv=10).mean())# 得出最高的評分及相應的C值
print(max(fsx), c[fsx.index(max(fsx))])plt.figure(figsize=[20, 5])
plt.plot(c, fullx, label='full')
plt.plot(c, fsx, label='feature selection')
plt.legend()
plt.show()

得出最高的評分及相應的C值：

這樣我們就實現了在特征選擇的前提下，保持模型擬合的高效，現在，如果有一位醫生可以來為我們指點迷津，看看剩下的這些特征中，有哪些是對針對病情來說特別重要的，也許我們還可以繼續降維。當然，除了嵌入法，系數累加法或者包裝法也是可以使用的。

比較麻煩的系數累加法

系數累加法的原理非常簡單。coef_雖然返回的是特征的系數，但是系數的大小和決策樹中的feature_importances_以及降維算法中的可解釋性方差explained_vairance_概念相似，其實都是衡量特征的重要程度和貢獻度的。在PCA中，我們通過繪制累積可解釋方差貢獻率曲線來選擇超參數，在邏輯回歸中，我們可以使用系數coef_來這樣做。

并且我們選擇特征個數的邏輯也是類似的：找出曲線由銳利變平滑的轉折點，轉折點之前被累加的特征都是我們需要的，轉折點之后的我們都不需要。不過這種方法相對比較麻煩，因為我們要先對特征系數進行從大到小的排序，還要確保我們知道排序后的每個系數對應的原始特征的位置，才能夠正確找出那些重要的特征。如果要使用這樣的方法，不如直接使用嵌入法來得方便。

簡單快速的包裝法

相對的，包裝法可以直接設定我們需要的特征個數，邏輯回歸在現實中運用時，可能會有”需要5~8個變量”這種需求，包裝法此時就非常方便了。不過邏輯回歸的包裝法的使用和其他算法一樣，并不具有特別之處，因此在這里就不在贅述，包裝法具體參考03期：特征選擇中的包裝法。

2.5 樣本不平衡與參數class_weight

樣本不平衡是指在一組數據集中，標簽的一類天生占有很大的比例，或誤分類的代價很高，即我們想要捕捉出某種特定的分類的時候的狀況。

什么情況下誤分類的代價很高?例如，我們現在要對潛在犯罪者和普通人進行分類，如果沒有能夠識別出潛在犯罪者，那么這些人就可能去危害社會，造成犯罪，識別失敗的代價會非常高，但如果，我們將普通人錯誤地識別成了潛在犯罪者，代價卻相對較小。所以我們寧愿將普通人分類為潛在犯罪者后再人工甄別，但是卻不愿將潛在犯罪者分類為普通人，有種"寧愿錯殺不能放過"的感覺。

再比如說，在銀行要判斷"一個新客戶是否會違約"，通常不違約的人vs違約的人會是99: 1的比例，真正違約的人其實是非常少的。這種分類狀況下，即便模型什么也不做，全把所有人都當成不會違約的人，正確率也能有99%,這使得模型評估指標變得毫無意義，根本無法達到我們的“要識別出會違約的人"的建模目的。

因此我們要使用參數class_weight對樣本標簽進行一定的均衡，給少量的標簽更多的權重，讓模型更偏向少數類，向捕獲少數類的方向建模。該參數默認None，此模式表示自動給與數據集中的所有標簽相同的權重，即自動1：1。當誤分類的代價很高的時候，我們使用”balanced“模式，我們只是希望對標簽進行均衡的時候，什么都不填就可以解決樣本不均衡問題。

但是，sklearn當中的參數class_weight變幻莫測，大家用模型跑一跑就會發現，我們很難去找出這個參數引導的模型趨勢，或者畫出學習曲線來評估參數的效果，因此可以說是非常難用。我們有著處理樣本不均衡的各種方法，其中主流的是采樣法，是通過重復樣本的方式來平衡標簽，可以進行上采樣（增加少數類的樣本），比如SMOTE，或者下采樣（減少多數類的樣本）。對于邏輯回歸來說，上采樣是最好的辦法。在案例中，會給大家詳細來講如何在邏輯回歸中使用上采樣。