【自然語言處理】【Scaling Law】語言模型物理學第3.3部分：知識容量Scaling Laws

語言模型物理學3.3：知識容量Scaling Laws

論文名稱：Physics of Language Models: Part 3.3, Knowledge Capacity Scaling Laws

論文地址：https://arxiv.org/pdf/2404.05405

相關博客
【自然語言處理】【Scaling Law】Observational Scaling Laws：跨不同模型構建Scaling Law
【自然語言處理】【大模型】語言模型物理學第3.3部分：知識容量Scaling Laws
【自然語言處理】Transformer中的一種線性特征
【自然語言處理】【大模型】DeepSeek-V2論文解析
【自然語言處理】【大模型】BitNet：用1-bit Transformer訓練LLM
【自然語言處理】BitNet b1.58：1bit LLM時代
【自然語言處理】【長文本處理】RMT：能處理長度超過一百萬token的Transformer
【自然語言處理】【大模型】MPT模型結構源碼解析(單機版)
【自然語言處理】【大模型】ChatGLM-6B模型結構代碼解析(單機版)
【自然語言處理】【大模型】BLOOM模型結構源碼解析(單機版)

一、簡介

? Scaling laws描述了模型尺寸與其能力的關系。不同于先前通過loss或者基準來評估模型能力，本文評估模型存儲的知識數量。這里主要是關注以元組方式表示的知識，例如(USA, capital, Washington D.C)。通過多個受控數據集，發現每個參數僅能存儲2 bit的知識，即使參數量化為8bit也有相同結論。因此，7B模型能夠存儲14B bit的指數，超過了英文Wikipedia和教科書的總和。

二、預備知識

? 知識片段(knowledge picec)：三個字符串組成的元組 $\text{(name,attribute,value)=(n,a,v)}$ 。例如， $\text{n="張三"}$ ， $\text{a="生日"}$ 且 $\text{v=1992年10月1日}$ 。

1. 知識的理論設定

? 一組知識的復雜度不僅由知識片段的數量決定，也取決于 $v$ 的長度、詞表多樣性和一些其他的隱藏。例如，若 $a$ 表示身份證號，則其包含的知識量比 $a$ 為性別要多，因為身份證號多樣性更高。此外，若 $a$ 為生日，則 $v$ 由3個塊(chunks)組成，例如(1996,10,1)。

? 基于這些觀察，列出一些可能影響知識復雜度的超參數：

N：名稱(name) $n$ 的數量，名稱集合表示為 $\mathcal{N}$ ；
K：屬性(attribute) $a$ 的數量，令 $\mathcal{A}$ 表示屬性集合，則 $|\mathcal{A}|=K$ ；
T：token的數量，令 $v$ 中的每個字符都屬于集合 $\mathcal{T}$ ，則有 $|\mathcal{T}|=T$ 。因此，T也可以認為是tokenizer中詞表大小；
C和L：塊(chunk)的數量以及每個塊的長度。 $v\in(\mathcal{T}^L)^C$ 可以表示為 $v=(v_1,v_2,\dots,v_C)$ ，其中 $v_i\in\mathcal{T}^L$ ；
D：塊(chunk)的多樣性。對于每個知識片段 $(n, a, v)$ ，若塊 $v_i$ 屬于 $\mathcal{D}_a\subset\mathcal{T}^L$ ，則塊的多樣性表示為 $D\overset{\text{def}}{=}|\mathcal{D}_a|\ll T^L$ ；

? 為了簡化表示，令屬性 $a\in\mathcal{A}$ 內的所有塊(chunk)共享多樣性集合 $\mathcal{D}_a$ 且所有塊均有相同長度。這里先引入 $\text{bioD(N,K,C,D,L,T)}$ 數據集，定義如下：

定義2.2

? 假設屬性集合 $\mathcal{A}$ 中有K個屬性，例如 $\mathcal{A}=\{\text{"ID1"}\dots\text{"ID K"}\}$ ；候選名稱集合 $\mathcal{N}_0(N_0\overset{\text{def}}{=}|\mathcal{N}_0|\gg N)$ 。

從 $\mathcal{N}_0$ 中均勻采樣N個名稱，形成集合 $\mathcal{N}$ ；
對于每個屬性 $a\in\mathcal{A}$ ，均勻隨機生成D個不同的字符串 $w_{1,a},\dots,w_{D,a}\in\mathcal{T}^L$ ，從而形成多樣性集合 $\mathcal{D}_a$ ；
對于每個名稱 $n\in\mathcal{N}$ 和屬性 $a\in\mathcal{A}$ ，通過均勻采樣 $v_i\in\mathcal{D}_a$ 來生成取值 $v^{\star}(n,a)=(v_1,v_2,\dots,v_C)$ ；

令 $\mathcal{Z}\overset{\text{def}}{=}\{(n,a,v^{\star}(n,a))\}_{n\in\mathcal{N},a\in\mathcal{A}}$ 表示知識集合。

命題2.3 bit復雜度上界

? 給定 $\mathcal{N}_0$ 、 $\mathcal{A}$ 和 $\mathcal{T}$ ，描述由定義2.2生成的知識集合，至多需要的bit數為
$\log_2\Big(\begin{matrix}|\mathcal{N}_0| \\ N \end{matrix}\Big)+ NKC\log_2 D+K\log_2\Big(\begin{matrix}T^L \\ D \end{matrix}\Big) \approx N\log_2\frac{|\mathcal{N}_0|}{N}+NKC\log_2 D+KD\log_2\frac{T^L}{D} \\$
從 $\mathcal{N}_0$ 中挑選N個名稱形成 $\mathcal{N}$ 的可能性包含 $\Big(\begin{matrix}|\mathcal{N}_0| \\ N \end{matrix}\Big)$ 種，需要的bit數為 $\log_2\Big(\begin{matrix}|\mathcal{N}_0| \\ N \end{matrix}\Big)$ ；

N個名稱，K個屬性，C個塊，每個塊有D種可能性，需要的bit數為 $NKC\log_2 D$ ；

K個屬性，每個屬性從 $T^L$ 的可能空間中挑選D個作為多樣性集合，需要的bit數為 $K\log_2\Big(\begin{matrix}T^L \\ D \end{matrix}\Big)$ ；

2. 知識的經驗設定

? 這里使用定義2.2生成的bioD數據集和其他一些人物簡介數據集來評估LM的scaling law。

? Allen-Zhu和Li構造了一個合成人物簡介數據集，包含N個人物且每個人物具有6個屬性：生日、出生城市、大學、專業、雇主和工作城市。為了將bioS數據集中的元組翻譯為自然語言，每個人通過6個隨機選擇的句子模板進行描述。

? 本文中，探索了該數據集的三種變體：

$\text{bioS(N)}$ 表示包含N個人物的在線數據集，每個人物都是通過動態選擇和排序6個句子模板來隨機生成的；
$\text{bioS}^{\text{simple}}(N)$ 表示類似的數據集，但是每個人物都是通過對句子模板進行固定的隨機選擇和排序；
$\text{bioR(N)}$ 表示相同的數據集，但是每個人物都通過LLaMA2重寫40次，從而增加真實性和多樣性；

? 這些數據集對應"bioS multi+permute"、“bioS single+permute"和"bioR multi”。先前的研究將N限制在100K，本文則將bioS中的N限制在20M，而bioR的N限制在1M。通過這樣的方式構造的數據集達到22GB。

? 若每個知識片段在訓練時見過1000次，則稱為1000次曝光。對于bioS(N)，1000次曝光不太可能包含相同的人物數據，因為每個屬性有50個句子模板，那么每個人就有 $50^6\times 6!$ 個可能的人物傳記。對于 $\text{bioS}^{\text{simple}}(N)$ ，1000次曝光意味著1000次數據通過。對于bioR(N)，1000/100曝光意味著訓練數據僅有25/2.5通過。

? 對于bioD數據集，定義 $\mathcal{N}_0$ 與bioS相同， $|\mathcal{N}_0|=400\times 400\times 1000$ 。通過使用隨機句子順序和一致的句子模板，將單個人物的屬性封裝在同一個段落中。例如
$\text{Anya Briar Forger's ID 7 is }v_{7,1},\dots,v_{7,C}.\text{ Her ID 2 is }v_{2,1},\dots,v_{2,C}.[\dots]\text{ Her ID 5 is }v_{5,1},\dots,v_{5,C}$
本文主要利用bioS。為了能夠表明更廣泛的適用性并且更好的連接理論邊界，也會報告 $\text{bioS}^{\text{simple}}$ 、 $\text{bioR}$ 和 $\text{bioD}$ 。

3. 模型和訓練

? 將GPT2的位置編碼換為RoPE并且禁用dropout。 $\text{GPT2-l-h}$ 表示 $l$ 層、 $h$ 頭且隱藏層維度為 $64 h$ 的模型，例如GPT2-small對應于GPT2-12-12。使用默認的GPT2Tokenizer，將人物的姓名和屬性轉換為變長token序列。后續在測試模型結構的scaling law時，也會使用LLaMA/Mistral架構。

? 使用特定的數據集從頭開始訓練語言模型。人物的知識片段被隨機拼接，使用進行分隔，然后隨機劃分為512 tokens的窗口。使用標準的自回歸損失函數進行訓練。

三、Bit復雜度下界

? 當評估模型中存儲的知識，不能簡單的依賴于平均的、逐個單詞的交叉熵損失值。例如，短語“received mentorship and guidance from faculty members”中不包含有用的知識。相反，應該關注知識tokens的損失值之和。

? 考慮具有權重 $W\in\mathcal{W}$ 的模型 $F$ 。假設 $F$ 在一個bioD(N,K,C,D,L,T)數據集 $\mathcal{Z}$ 上訓練，該過程表示為 $W=W(\mathcal{Z})$ 。在評估階段，通過兩個函數來表示 $F$ ： $F^\top(W,R)$ 用來生成名稱、 $F^{\perp}(W,n,a,R)$ 表示在給定(n,a)的情況下生成具體的取值， $R$ 表示生成中使用的隨機性。令 $F^{\perp}_1(W(\mathcal{Z}),n,a,R)$ 表示 $F^{\perp}(W(\mathcal{Z}),n,a,R)$ 生成的第一個分塊(chunk)。通過計算下面的三個交叉熵損失來評估 $F$ ：
$\begin{align} \textbf{loss}_{name}(\mathcal{Z})&\overset{\text{def}}{=}\mathbb{E}_{n\in\mathcal{N}}-\log\textbf{Pr}_{R}[F^\top(W(\mathcal{Z}),R)=n] \\ \textbf{loss}_{value1}(\mathcal{Z})&\overset{\text{def}}{=}\mathbb{E}_{n\in\mathcal{N},a\in\mathcal{A}}-\log\textbf{Pr}_R[F_1^\top(W(\mathcal{Z}),n,a,R)=v_{1}^{\star}(n,a)] \\ \textbf{loss}_{value}(\mathcal{Z})&\overset{\text{def}}{=}\mathbb{E}_{n\in\mathcal{N},a\in\mathcal{A}}-\log\textbf{Pr}_R[F^{\perp}(W(\mathcal{Z}),n,a,R)=v^{\star}(n,a)] \\ \end{align} \\$
? 對于一個語言模型，這些量可以通過自回歸交叉熵損失進行計算。例如，在句子" $\text{Anya Briar Forger's ID 7 is }v_{7,1},\dots,v_{7,C}$ "中評估模型，通過在token "Anya Briar Forger"上的loss進行求和能夠精準計算出當 $n=\text{"Anya Briar Forger"}$ 時的 $-\log\textbf{Pr}_{R}[F^\top(W(\mathcal{Z}),R)=n]$ 。將token $v_{7,1}$ 的損失值進行求和則計算出n和a="ID 7"時的 $-\log\textbf{Pr}_R[F_1^\top(W(\mathcal{Z}),n,a,R)=v_{7,1}]$ 。在整個序列 $v_{7,1},\dots,v_{7,C}$ 上的損失值求和則有 $-\log\textbf{Pr}_R[F^{\perp}(W(\mathcal{Z}),n,a,R)=v_{7,1},\dots,v_{7,C}]$ 。

定理3.2 (bit復雜度的下界)

假設 $N\geq\Omega(D\log N)$ ，則有
$\begin{align} \log_2 |\mathcal{W}|&\geq\mathbb{E}_{\mathcal{Z}}\Big[N\log_2\frac{N_0-N}{e^{\textbf{loss}_{name}(\mathcal{Z})}}+NK\log_2\frac{D^C}{e^{\textbf{loss}_{value}(\mathcal{Z})}}+KD\log_2\frac{T^L-D}{De^{(1+o(1))\textbf{loss}_{value1}(\mathcal{Z})}}-o(KD)\Big] \\ &=N\log_2\frac{N_0-N}{e^{\mathbb{E}_{\mathcal{Z}}\textbf{loss}_{name}(\mathcal{Z})}}+NK\log_2\frac{D^C}{e^{\mathbb{E}_{\mathcal{Z}}\textbf{loss}_{value}(\mathcal{Z})}}+KD\log_2\frac{T^L-D}{De^{(1+o(1))\mathbb{E}_{\mathcal{Z}}\textbf{loss}_{value1}(\mathcal{Z})}}-o(KD) \\ \end{align} \\$
本文的目標是就研究模型參數數量與這個下界的關系。

推論3.3 (理想無誤差的情況)

? 理想情況下，對于 $\mathcal{Z}$ 中的每個數據， $F$ 都能以1/N的概率從 $\mathcal{N}$ 中生成名稱，那么有 $\textbf{loss}_{name}(\mathcal{Z})=\log N$ ；給定(n,a)樣本對， $F$ 能夠100%準確生成v，那么 $\textbf{loss}_{value}(\mathcal{Z})=\textbf{loss}_{value1}(\mathcal{Z})=0$ 。在這種情況下，
$\log_2 |\mathcal{W}|\geq N\log_2\frac{N_0-N}{N}+NKC\log_2 D+KD\log_2\frac{T^L-D}{D}-o(KD) \\$

三部分進行求和是獲得下界的必要條件，忽略其中任何一個都會導致次優下界；
研究固定數據集 $\mathcal{Z}$ 的下界是不可能的，即使沒有任何可訓練參數，模型也能硬編碼 $\mathcal{Z}$ 至其架構中。因此，需要考慮數據集分布上的下界。

? 若名稱是固定的 $(\mathcal{N}=\mathcal{N}_0)$ 并且具有N個知識片段，每個知識片段都是從固定集合 $[T]$ 中挑選出來的。那么，當滿足 $\log_2|\mathcal{W}|\geq N\log_2 T$ 時，任何模型 $F(\mathcal{W})$ 都能夠完美學習到這些知識。為了能夠與定理3.2聯系起來，需要解決三個挑戰。(1) 模型F僅能以一定程度的準確率來學習知識；(2) $\mathcal{N}\neq\mathcal{N}_0$ ，因此名稱需要進行學習，即使是完美的模型在生成名稱時都無法實現0交叉熵損失。(3) 知識片段之間存在依賴關系。

四、容量比

? 基于定理3.2，忽略低階項，定義經驗容量比為

定義4.1

? 給定一個具有 $P$ 個參數的模型 $F$ ，其在bioD(N,K,C,D,L,T)數據集 $\mathcal{Z}$ 上訓練。假設其能夠給出 $p_1=\textbf{loss}_{name}(\mathcal{Z})$ 、 $p_2=\textbf{loss}_{value}(\mathcal{Z})$ 、 $p_3=\textbf{loss}_{value1}(\mathcal{Z})$ ，定義容量比(capacity)和最大容量比(max capacity ratio)為
$R(F)\overset{\text{def}}{=}\frac{N\log_2\frac{N_0}{e^{p_1}}+NK\log_2\frac{D^C}{e^{p_2}}+KD\log_2\frac{T^L}{De^{p_3}}}{P} \\$

$R^{\max}(F)\overset{\text{def}}{=}\frac{N\log_2\frac{N_0}{N}+NKC\log_2 D+KD\log_2\frac{T^L}{D}}{P} \\$

? 必然滿足 $R(F)\leq R^{\max}(F)$ ，僅當模型是完美的情況下等號才成立。對于固定的數據集，進一步增大模型尺寸也不會增加額外的知識。因此，隨著模型尺寸P的增加， $R^{\max}(F)$ 會逐步趨近于0。對于bioS(N)數據，可以通過忽略多樣性項來略微降低容量比。

定義4.3

? 給定一個具有 $P$ 個參數的模型 $F$ ，其在bioS(N)數據集 $\mathcal{Z}$ 上訓練。假設其能夠給出 $p_1=\textbf{loss}_{name}(\mathcal{Z})$ 、 $p_2=\textbf{loss}_{value}(\mathcal{Z})$ ，其容量比為
$\begin{align} R(F)&\overset{\text{def}}{=}\frac{N\log_2\frac{N_0}{e^{p_1}}+N\log_2\frac{S_0}{e^{p_2}}}{P} \\ R^{\max}(F)&\overset{\text{def}}{=}\frac{N\log_2\frac{n_0}{N}+N\log_2 S_0}{P} \\ \end{align} \\$

忽略名稱，每個人包含 $\log_2(S_0)\approx47.6$ bit的知識。

五、基礎Scaling Laws

在這里插入圖片描述

? 使用bioS(N)數據集訓練了一系列GPT2模型。訓練的方式能夠確保每個知識片段都被訓練1000次，該過程稱為"1000次曝光"。下面是一些初步的結論：

通過訓練保證bioS(N)有1000次曝光，N的范圍從10K到10M，GPT2模型的尺寸從1M到0.5B。上圖1(a)顯示結果為：

峰值容量比R(F)始終大于2；
當 $R^{\max}(F)\leq 1.8$ 時，模型接近完美的知識準確率（數據集包含B bit的知識，那么模型參數量選擇 $P\geq B/1.8$ 就足夠了）；
對于所有的模型，均有 $R(F)\leq 2.3$ ；

? "2bit/param"并不是逐字逐句的記憶，這樣的知識可以靈活抽取并且能夠進一步在下游任務中操作。這是因為bioS(N)數據是知識增強的，人物簡介有充足的文本多樣性。

1. 數據格式：多樣性和重寫

? 在 $\text{bioS}^{\text{simple}}$ 和 $\text{bioR}$ 上執行相同的分析， $\text{bioS}$ 是 $\text{bioS}^{\text{simple}}$ 的文本多樣性版本， $\text{bioR}$ 是由LLaMA2生成的接近真實的人物簡介。

在相同1000次曝光，GPT2在 $\text{bioS}^{\text{simple}}$ 和 $\text{bioR}$ 上的峰值容量比都接近2。因此，多樣性數據并不會損壞模型容量，甚至可能會改善容量。

? 比較 $\text{bioS}$ 和 $\text{bioS}^{\text{simple}}$ ，同一個數據重寫1000次要比相同數據傳遞給模型1000個更有優勢。若數據失去多樣性，模型將會浪費容量記憶句子結構，從而降低容量。

? 在真實場景中，使用LLaMA2這種工具對預訓練數據進行重寫，就像 $\text{bioR}$ 那樣。重寫40次則產生40個不同的片段，那么需要40倍大的模型嗎？不需要，比較 $\text{bioS}$ 和 $\text{bioR}$ 表明訓練相同時間，模型容量比基本相同。

? Allen-Zhu and Li表明，重寫預訓練數據對于知識抽取而不是逐字記憶至關重要。然而，他們并沒探索模型容量的影響。本文解決了這個問題，表明重寫預訓練數據并不會損害模型的知識容量，甚至有可能增強。

2. 參數化Scaling Laws

? 進一步研究了 $\text{bioD(N,K,C,D,L,T)}$ 數據上的scaling laws。不同于人物簡介數據中的變量僅有N， $\text{bioD}$ 數據集允許更靈活的操作超參數K,C,D,L,T。這允許進一步測試這些參數對模型容量的影響。

跨越各種取值，K和G的范圍從1到50，D的范圍從10到10000，L從1到50，T從20到40000，觀察到的結果：GPT2模型的峰值容量比始終有 $R(F)\geq 2$ 。

六、訓練時間與Scaling Law

? 當模型沒有被充分訓練會怎樣？例如，每個知識在預訓練階段僅出現100次。令 $\text{bioS}(N)$ 曝光100次來計算容量比，可以發現：

當訓練過程中 $\text{bioS(N)}$ 數據僅曝光100次，N從10K到10M，GPT2模型尺寸從1M到0.5B，峰值容量比始終滿足 $R(F)\geq 1$ 。

? 因此，雖然1000次曝光可能是達到最大容量的必然條件，但僅曝光100次也不會有很多損失。

七、模型結構與Scaling Law

? 目前有很多transformer架構被使用，其中LLaMA和Mistral是其中比較常見的。就知識容量來說，在充足訓練下，GPT2結構并沒有比其他結構更差。

在1000次曝光設定下，架構并不重要：

LLaMA結構在小模型上略微不如GPT2，但是這個差距隨著參數增大而緩解；
Mistral結構也能觀察到類似現象；
降低GPT2中MLP尺寸的1/4，甚至消除所有的MLP層都不影響容量比。這表明，不同于傳統認知，注意力層也能夠存儲知識。

? 這表明 2bit/param容量比在大多數典型語言模型結構中是一個相對普遍的規律。

在100次曝光設置中：

即使是更大的模型，LLaMA結構的容量比也比GPT2差1.3倍。Mistral也有類似的結果。
降低GPT2中MLP尺寸的1/4，對容量比影響微不足道。
移除MLP會降低容量比1.5倍以上。

? 為了能夠明確在100次曝光設定中，LLaMA結構為什么差于GPT2，逐步修改LLaMA結構至GPT2來確定關鍵的結構變化。

對于大模型，將LLaMA結構中的gated MLP替換為標準MLP，顯著提高了LLaMA的容量比。
對于小型LLaMA模型，將其轉換為GPT2Tokenizer是匹配GPT2效果的必要條件，盡管這不是主要問題。
其他一些修改，例如將silu修改為gelu或者為LayerNorm添加可訓練偏差，都不會顯著影響容量比。

八、量化與Scaling Law

? 模型訓練和測試都使用16bit浮點數。在訓練后使用int8/int4量化會有什么影響呢？

對16bit訓練的語言模型進行量化：

int8對容量來說可以忽略不計；
int4使得容量減少2倍以上；

? 對于峰值容量為2 bits/param，量化至int8不會對容量有影響。在高質量數據上進行1000次曝光能夠達到的最優容量比為2 bits/param，那么可以得出結論：即使進一步訓練也無法改善容量，但是量化可以。由于int8模型的容量比具有絕對上界 $R(F)\leq 8$ ，因此

像GPT2這樣的語言模型，能夠超過絕對理論限制的1/4來存儲知識。

? LLM能夠壓縮知識至其參數空間中，從而實現2bit/param。那么這些知識是如何存儲的呢？本文認為知識以不太冗余的方式存儲在模型中。不太可能是MLP層單獨存儲知識，因為注意力層也能夠存儲知識。此外，當模型接近容量極限的時候，移除L層模型中的最后一層，余下的知識顯著小于 $1-\frac{1}{L}$ 。這也就表明知識不是單獨存儲在獨立的層，而是以復雜的方式進行存儲。

九、MoE與Scaling Law

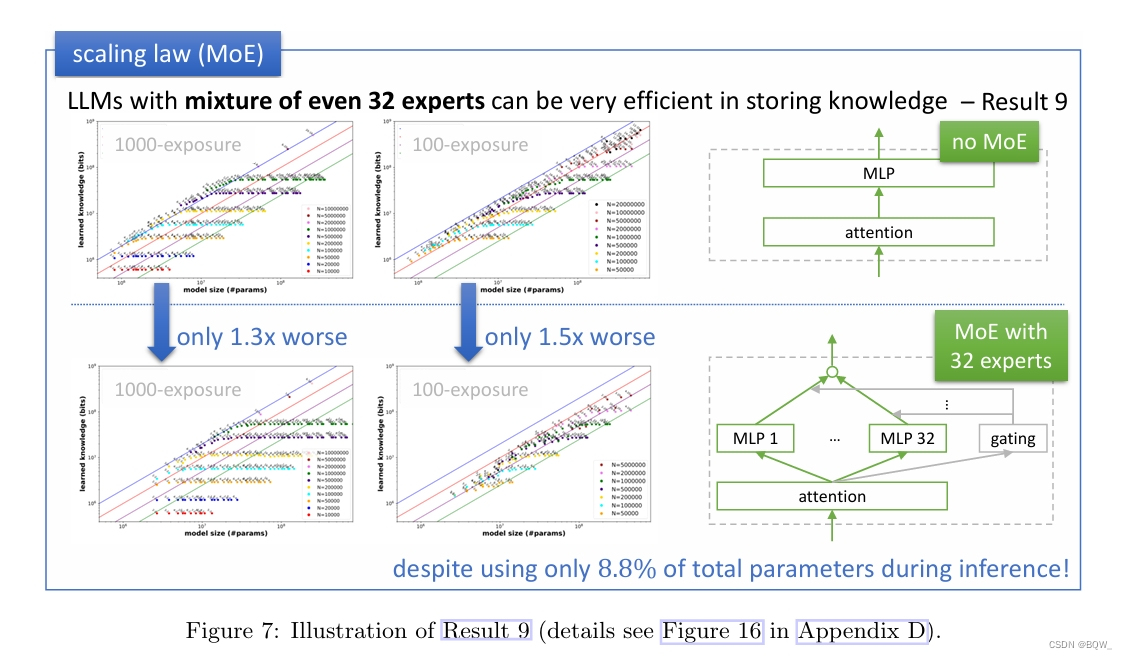
在這里插入圖片描述

? MoE模型在容量比方面會有所不同嗎？對于一個MoE模型，令P表示模型中的總參數量，包括所有專家。由于其稀疏性，有效參數數量顯著小于P。

? 考慮一個GPT2模型，但是MLP層替換為32個專家，每個專家遵循 $d\rightarrow d\rightarrow d$ 的配置。這種設置總共會使用 $64d^2$ 的總參數，但是在推理時每個token僅使用 $2d^2$ 參數。考慮了具有 $4d^2$ 參數的注意力層，具有32個專家的MoE模型總參數量和有效參數量比值接近于 $\frac{4d^2+64d^2}{4d^2+2d^2}\approx 11.3$ 。