Value at Risk(VaR)是一種統計技術,用于量化投資組合在正常市場條件下可能遭受的最大潛在損失。它是風險管理和金融領域中一個非常重要的概念。VaR通常以貨幣單位表示,用于估計在給定的置信水平和特定時間范圍內,投資組合可能遭受的最大損失。例如,一個1%的一日VaR為$1百萬意味著在任何給定的日子里,只有1%的概率投資組合的損失會超過100萬美元。
VaR的主要特點和考慮因素包括:
置信水平:這是VaR計算中的一個關鍵參數,表示損失不會超過VaR估計的概率。常見的置信水平有95%、99%等。
時間范圍:VaR估計的另一個關鍵方面是時間范圍,比如一天、一周或一個月。時間范圍越長,潛在損失的估計通常越大。
損失的估計:VaR提供了一個損失估計,但并不預測損失會發生的確切時間點。
方法論:計算VaR的方法有多種,包括歷史模擬法、方差-協方差法和蒙特卡洛模擬法。每種方法都有其優缺點,適用于不同類型的投資組合。
局限性:雖然VaR是一個有用的風險度量工具,但它也有局限性。它不考慮超過VaR估計值的極端損失,且對于非線性和復雜的金融工具可能不夠精確。
VaR在金融領域廣泛應用,特別是在風險管理、資產管理和資本要求計算方面。銀行、投資公司和其他金融機構使用VaR來監控和管理其暴露在市場、信用和其他風險中的資產組合。盡管它是一個有力的工具,但專業人士和監管機構都認識到,依賴單一風險度量標準是不足夠的,需要結合其他風險管理技術和工具。
這里我選取的是googel的股票,使用dailyReturn函數算出它的收益率,前五行如下:
# 計算股票的日度收益率 # 計算對數收益率
returns <- dailyReturn(GOOGL)
returns
# 繪制收益率時序圖
plot(returns, main = "Daily Returns of Alphabet (GOOGL) in the Last Year", ylab = "Daily Returns")# 計算收益率的均值、方差和標準差
mean_return <- mean(returns, na.rm = TRUE)
variance <- var(returns, na.rm = TRUE)
std_deviation <- sd(returns, na.rm = TRUE)# 輸出均值、方差和標準差
print(paste("Mean of returns:", mean_return))
print(paste("Variance of returns:", variance))
print(paste("Standard deviation of returns:", std_deviation))???????????daily.returns
2023-08-15 -0.0100686499
2023-08-16 -0.0083217753
2023-08-17 ?0.0094794095
2023-08-18 -0.0189347291
2023-08-21 ?0.0071394947
接下來可視化:

接下來分別使用mean,var,sd函數進行算出結果:
Mean of returns: 0.000487064370016916
Variance of returns: 0.000277345687220339
Standard deviation of returns: 0.0166536989050583
對該股票采用Weibul1分布法估計其180天周期90%置信水平的VaR序列(用前180天歷史數據預測未來180天的日度VaR,并畫出Va 時序圖
# 自定義 Weibull 分布的估計函數
weibull_func <- function(data) {fit <- suppressWarnings(tryCatch(fitdistr(data, densfun = "weibull",start = list(shape = 1, scale = 1), # 自定義合適的初始參數值method = "BFGS"), # 自定義擬合方法error = function(e) NULL))return(fit)
}# 進行 Weibull 分布的擬合
fit_weibull <- weibull_func(positive_returns)# 使用擬合的 Weibull 分布計算 VaR
confidence_level <- 0.9
VaR_90 <- qweibull(1 - confidence_level, shape = fit_weibull$estimate[1], scale = fit_weibull$estimate[2])90% 置信水平的 VaR: 0.0023112336283049
計算所有日期的 VaR并畫圖

另選一只股票,采用排序法計算其一年期 70%置信度的日度 VaR,若回測時次日跌幅超過 VaR 預測的闖值,則判定為一次“違約’。采用交易量、拆幅(最高價減最低價)和收益率MACDKDJOBVCCI等來預測違約估計 logit 模型,然后評價你的模型效果 (NP、ROC、CAP),并提出些可行改進方案。
這里選取的是APPLE的股票數據,設置API接口獲取:
同樣也是計算日度收益率,前5行如下:
???????????daily.returns
2023-08-15 ?0.0000000000
2023-08-16 -0.0049591434
2023-08-17 -0.0145551339
2023-08-18 ?0.0028160920
2023-08-21 ?0.0077368331
計算采用排序法計算其一年期 70%置信度的日度 VaR,若回測時次日跌幅超過 VaR 預測的闖值,則判定為一次“違約’。寫成相應的代碼:
var_70 <- quantile(returns, 0.3) ?# 70%分位數即為VaR
default_event <- ifelse(returns < var_70, 1, 0)
default_event
default_event輸出示例如下:
???????????daily.returns
2023-08-15 ????????????0
2023-08-16 ????????????0
2023-08-17 ????????????1
2023-08-18 ????????????0
2023-08-21 ????????????0
接下來分別計算各個特征并且最終合并文件:
# 計算日度收益率
returns <- dailyReturn(AAPL$AAPL.Close)
returns
# 計算VaR
var_70 <- quantile(returns, 0.3) # 70%分位數即為VaR
default_event <- ifelse(returns < var_70, 1, 0)
default_event# 計算交易量
volume <- AAPL$AAPL.Volume
volume
# 計算拆幅
range <- AAPL$AAPL.High - AAPL$AAPL.Low
range
# 計算收益率
returns <- dailyReturn(AAPL$AAPL.Close)
returns
# 計算技術指標
# 計算MACD指標
macd_data <- MACD(AAPL$AAPL.Close)
macd_data
# 計算KDJ指標
Hi <- AAPL$AAPL.High
Lo <- AAPL$AAPL.Low
Cl <- AAPL$AAPL.Close
# 假設N=9天
N <- 9# 計算RSV值
RSV <- (Cl - rollapplyr(Lo, width = N, min, align = "right")) / (rollapplyr(Hi, width = N, max, align = "right") - rollapplyr(Lo, width = N, min, align = "right")) * 100# 計算K值、D值和J值
K <- D <- J <- rep(NA, length(Cl))
for (i in N:length(Cl)) {if (i == N) {K[i] <- 50 # 初始K值為50D[i] <- 50 # 初始D值為50} else {K[i] <- (RSV[i] + (N - 1) * K[i - 1]) / ND[i] <- (K[i] + (N - 1) * D[i - 1]) / N}J[i] <- 3 * K[i] - 2 * D[i]
}# 將計算結果添加到數據框中
KDJ_data <- data.frame(Date = index(AAPL), K = K, D = D, J = J)
KDJ_data最終數據合并如下:
| macd | signal | K | D | J | OBV | |
| 2023-08-15 | 0.502 | 0.607 | 56.791 | 56.537 | 57.299 | 43622593 |
| 2023-08-16 | 0.502 | 0.607 | 56.791 | 56.537 | 57.299 | -3342264 |
| 2023-08-17 | 0.502 | 0.607 | 56.791 | 56.537 | 57.299 | -69405146 |
| 2023-08-18 | 0.502 | 0.607 | 56.791 | 56.537 | 57.299 | -8232996 |
| 2023-08-21 | 0.502 | 0.607 | 56.791 | 56.537 | 57.299 | 38078883 |
| 2023-08-22 | 0.502 | 0.607 | 56.791 | 56.537 | 57.299 | 80163128 |
| CCI | Returns | macd.1 | macd_data | Volume | default_event | |
| 2023-08-15 | 15.587 | 0.000 | 0.502 | 0.607 | 43622593 | 0 |
| 2023-08-16 | 15.587 | -0.005 | 0.502 | 0.607 | 46964857 | 0 |
| 2023-08-17 | 15.587 | -0.015 | 0.502 | 0.607 | 66062882 | 1 |
| 2023-08-18 | 15.587 | 0.003 | 0.502 | 0.607 | 61172150 | 0 |
| 2023-08-21 | 15.587 | 0.008 | 0.502 | 0.607 | 46311879 | 0 |
| 2023-08-22 | 15.587 | 0.008 | 0.502 | 0.607 | 42084245 | 0 |
# 建立邏輯回歸模型
# 建立 Logit 模型
model <- glm(default_event ~ ., data = train, family = binomial)
model
# 在測試集上進行預測
predicted <- predict(model, newdata = test, type = "response")
predicted
?
理想情況下,ROC 曲線會向左上角彎曲,靠近左上角的(0,1)點,這表明模型具有很高的真正例率和很低的假正例率。在這張圖中,曲線開始時沿著 y 軸急劇上升,表明在低假正例率下模型能夠實現相對較高的真正例率。總體而言,這個 ROC 曲線表明模型在某些閾值設置下對正類的預測有一定的準確性。
Area under the curve: 0.9074
曲線下面積(AUC)為 0.9074 表示模型具有很高的區分能力。
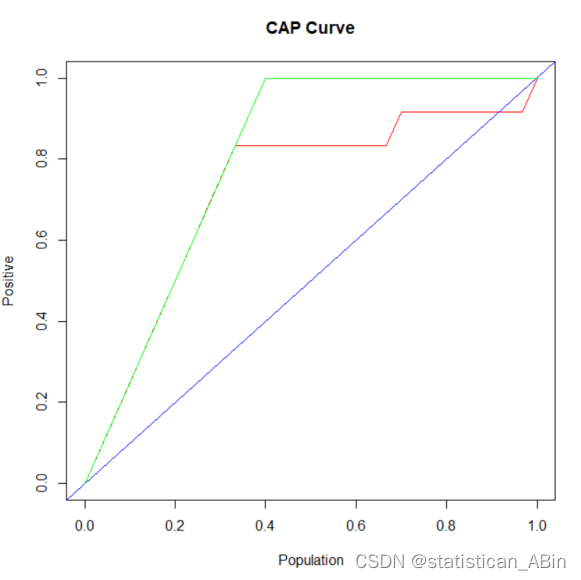
# 繪制 CAP 曲線
cap_curve <- function(actual, predicted) {total <- length(actual)num_positive <- sum(actual == 1)# 確保排序后的實際值和預測值長度一致actual_sorted <- actual[order(predicted, decreasing = TRUE)]# 計算累積正例的比例cum_positive <- cumsum(actual_sorted == 1) / num_positive# 生成 x 和 y 值x_values <- c(0, (1:total) / total)y_values <- c(0, cum_positive)# 確保 x_values 和 y_values 長度一致if (length(x_values) != length(y_values)) {stop("Lengths of x_values and y_values are not equal.")}# 繪制 CAP 曲線plot(x_values, y_values, type = "l", col = "red", xlab = "Population", ylab = "Positive", main = "CAP Curve")abline(0, 1, col = "blue") # 隨機預測線lines(c(0, sum(actual == 1) / total, 1), c(0, 1, 1), col = "green") # 理想曲線
}# 調用函數繪制 CAP 曲線
cap_curve(test_data$default_event, predictions)基于這些指標,以下是一些改進模型性能的策略:
數據重新采樣:如果數據集不平衡,即違約和非違約的案例數量有很大差異,可以嘗試過采樣少數類別或欠采樣多數類別。也可以使用合成數據生成技術,如 SMOTE,來合成新的正例。
特征工程:檢查是否有可能從現有數據中創建更有信息量的特征。評估并可能移除對預測不具有統計顯著性的特征。使用特征選擇技術來識別和保留最重要的特征。
模型調整:調整模型超參數,使用網格搜索或隨機搜索確定最佳參數。嘗試不同的模型算法,比如隨機森林、支持向量機或梯度提升機,并與當前的邏輯回歸模型比較。
閾值調整:改變分類的決策閾值,可能會提高正類別的預測準確性。
使用成本敏感學習,并為錯誤分類的類別分配不同的權重。
模型集成:使用集成方法如 Bagging 或 Boosting,這些方法可以提高模型的穩定性和性能。
考慮堆疊不同的模型來利用各自的優勢。
評估指標選擇:依據業務目標,選擇更合適的評估指標,例如利潤曲線,以確保模型優化方向與業務目標一致。
題目和代碼和數據
創作不易,希望大家多多點贊收藏和評論!

)
微服務拆分與nacos的配置使用)


--批量圖像查詢)



解決)



)





