集成學習
簡介
決策樹


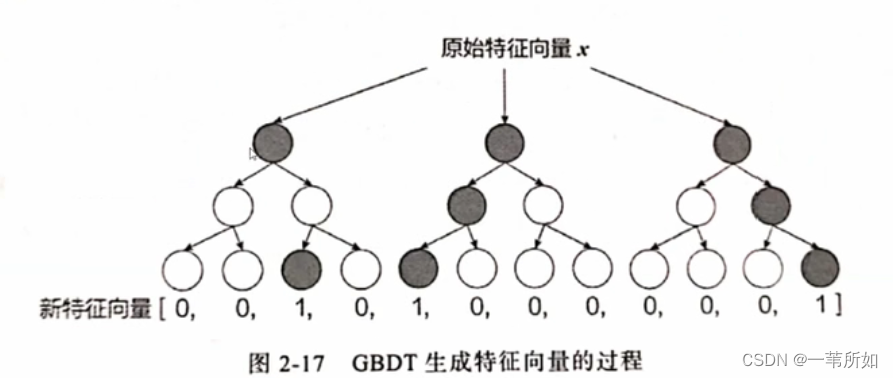
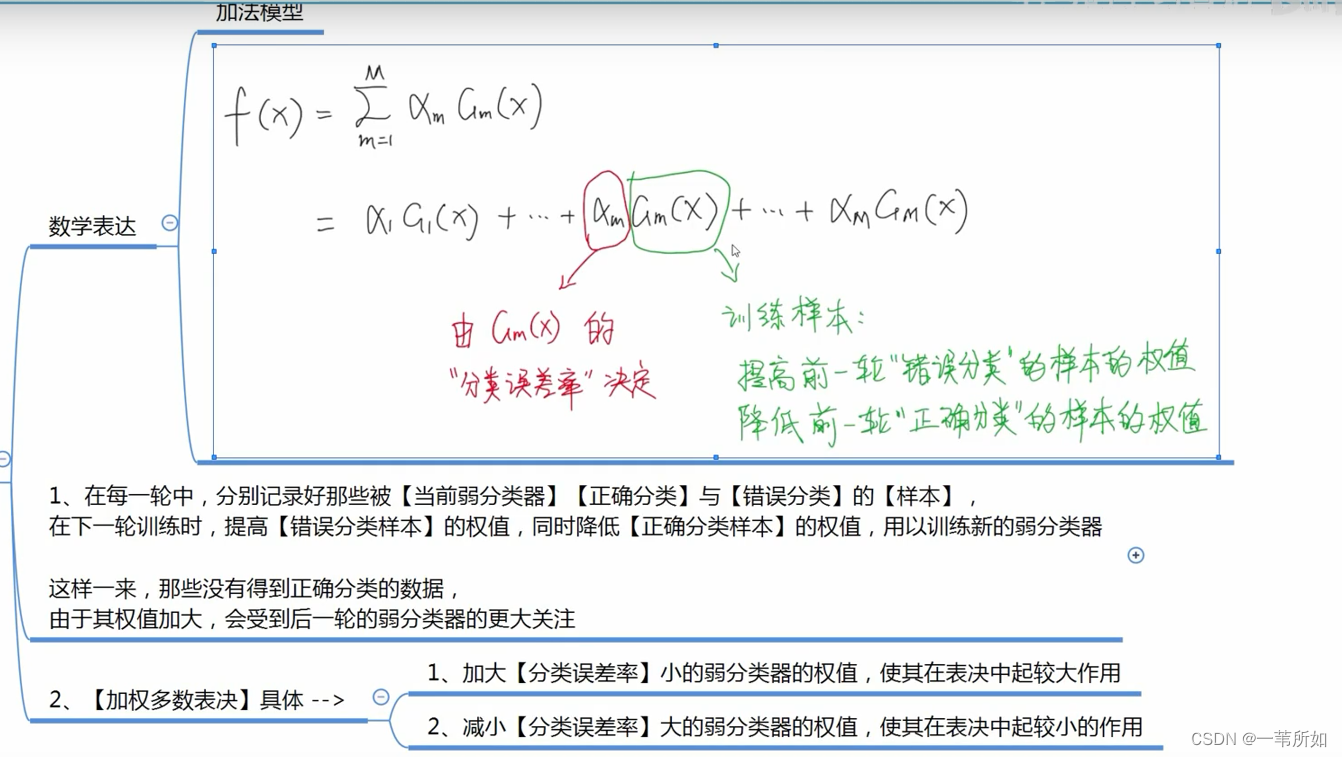
GBDT


擬合殘差



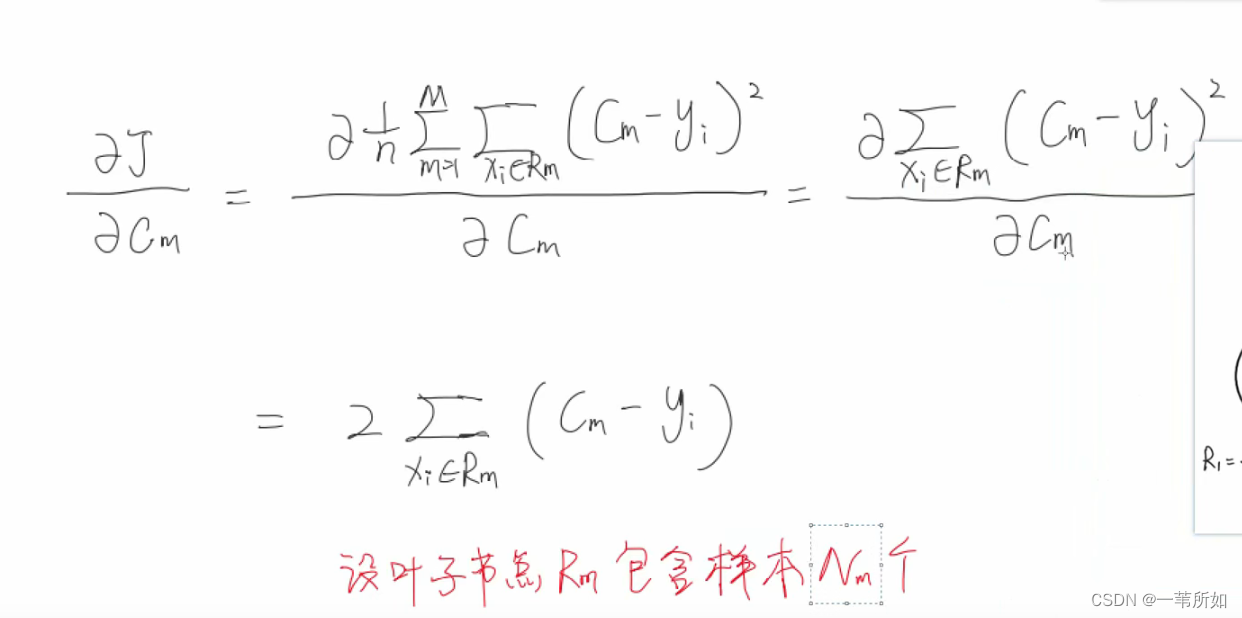
一般 GBDT



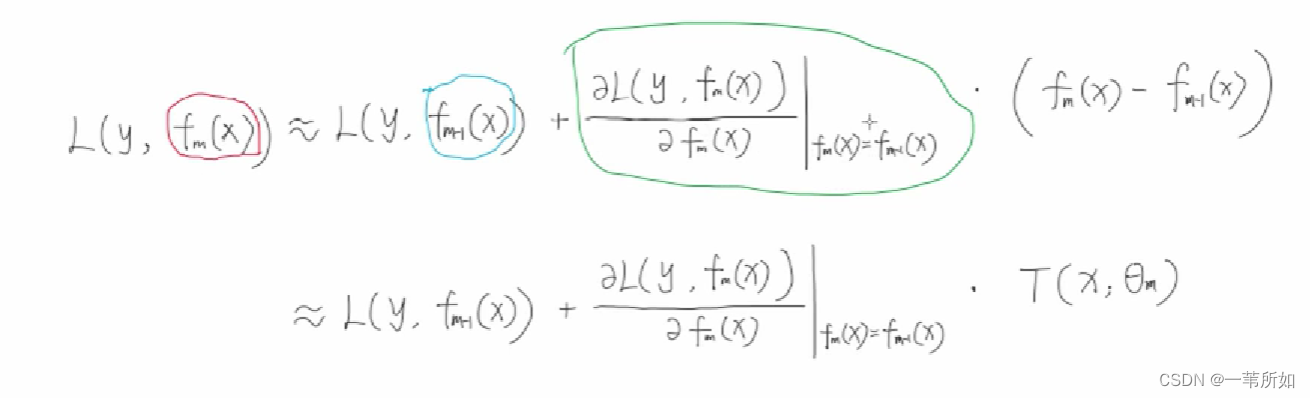
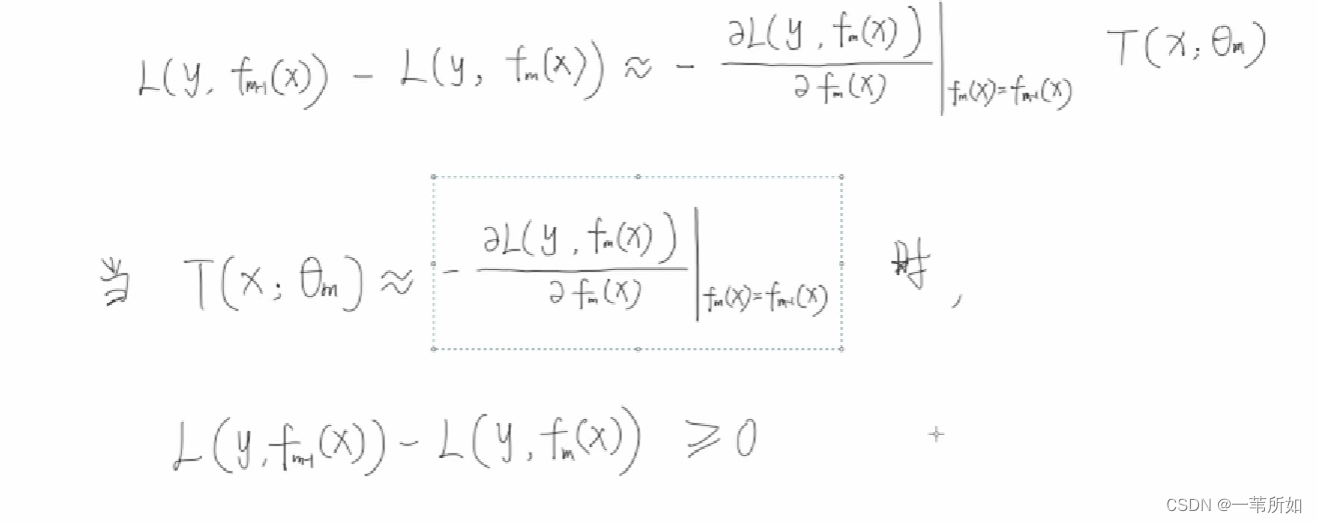





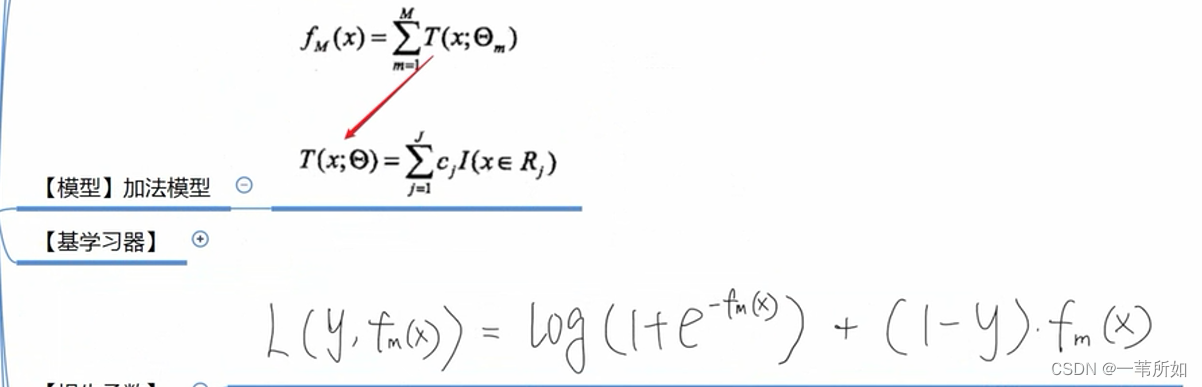

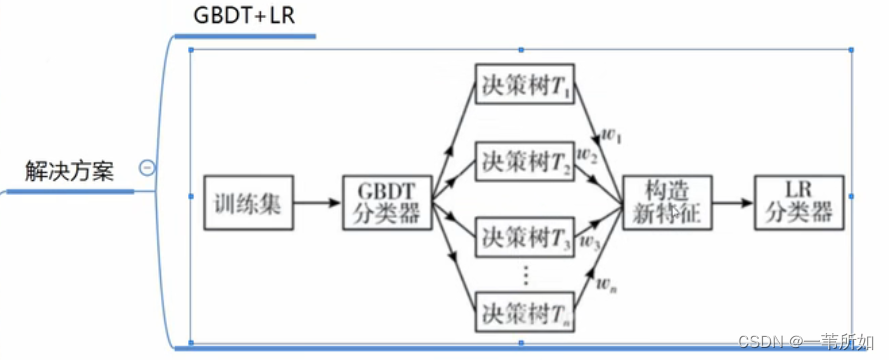

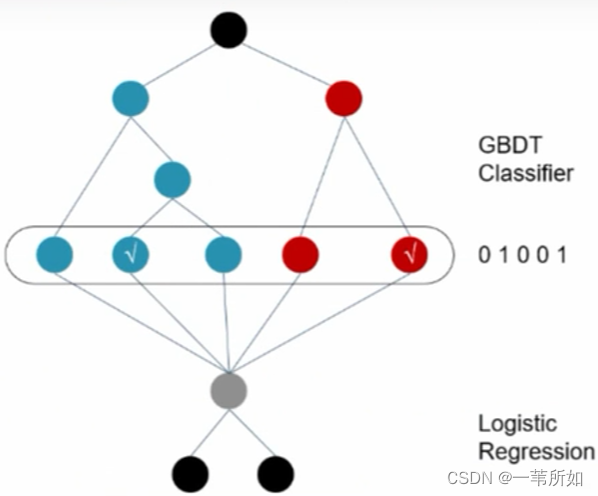

XGBOOST
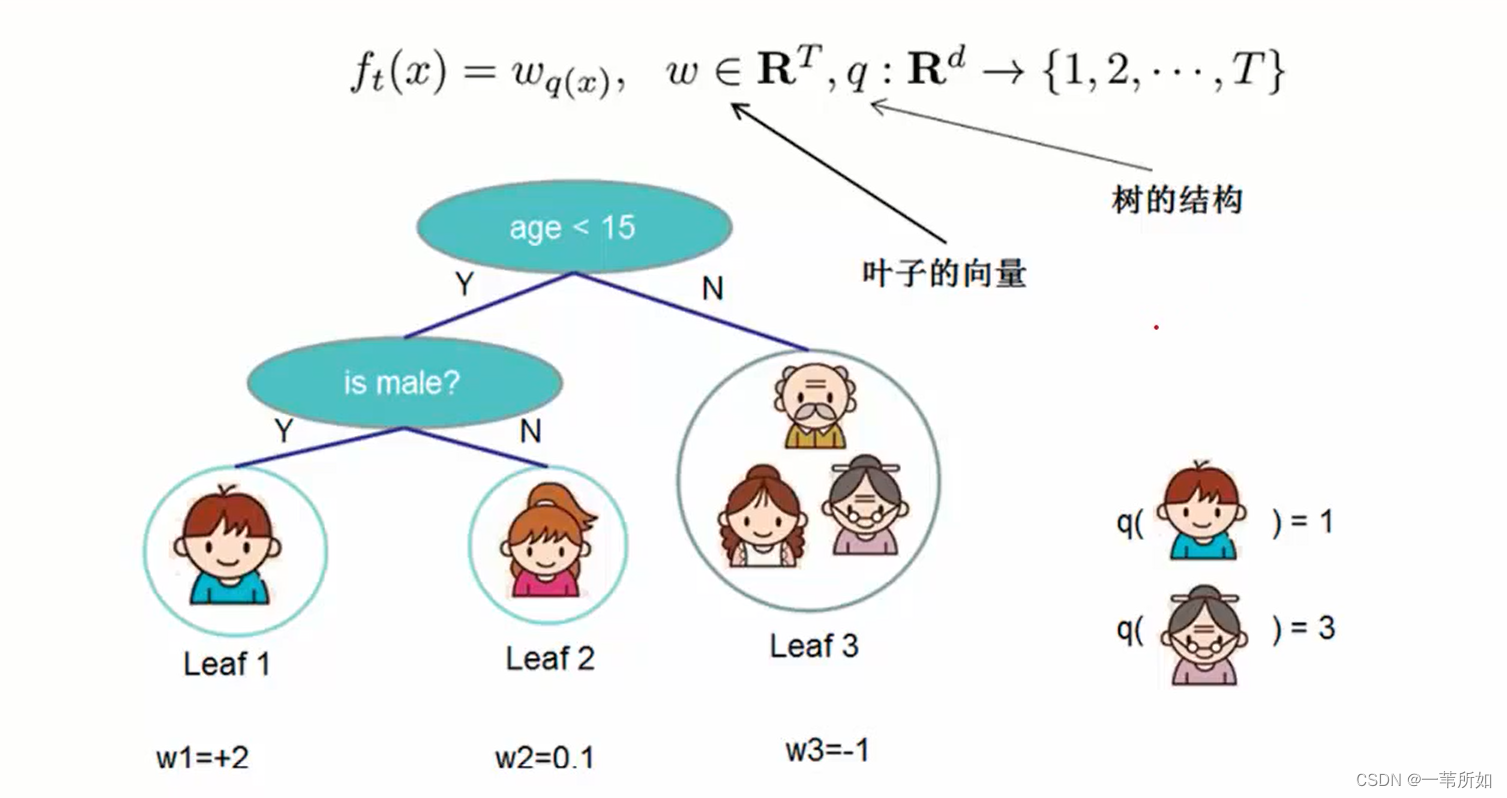
弓
1
能表達樣本落入的子節點,但是不能把表示結構

2

3.正則項 – 懲罰
防止過擬合,比如一個值總共有10顆樹都是由同一顆樹決定的,過擬合
5
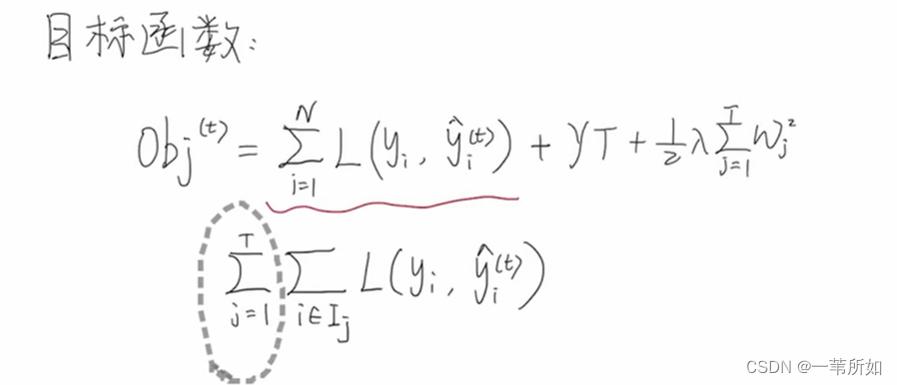
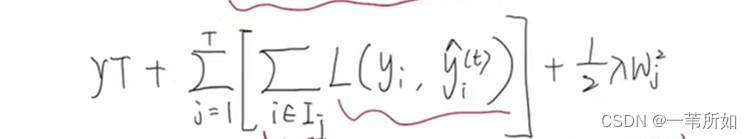
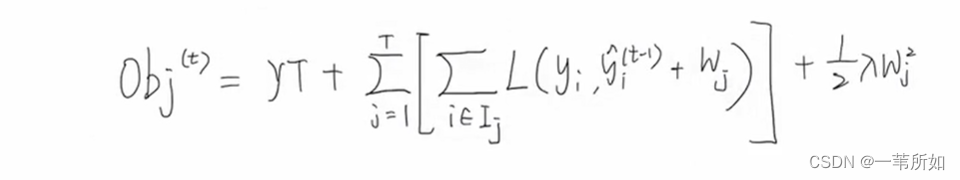
找到一種方式不依賴于損失函數 – 二階泰勒

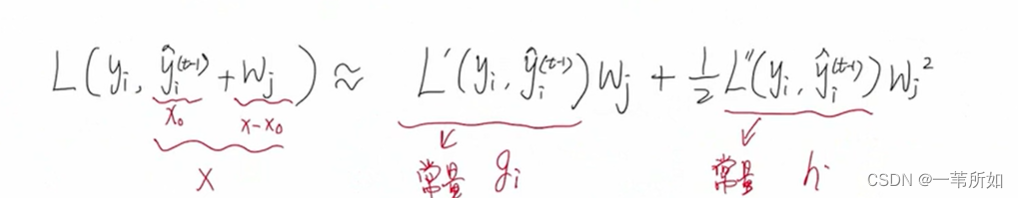
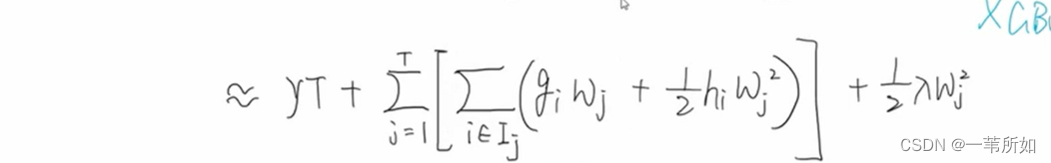
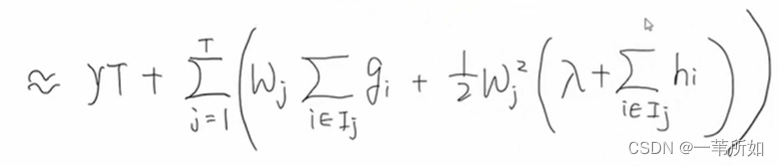 gi – 一階梯度 hi–二階梯度
gi – 一階梯度 hi–二階梯度
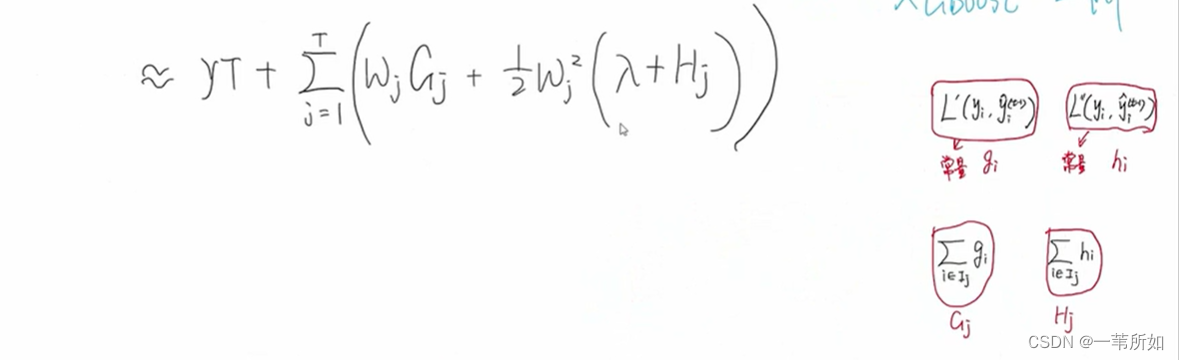
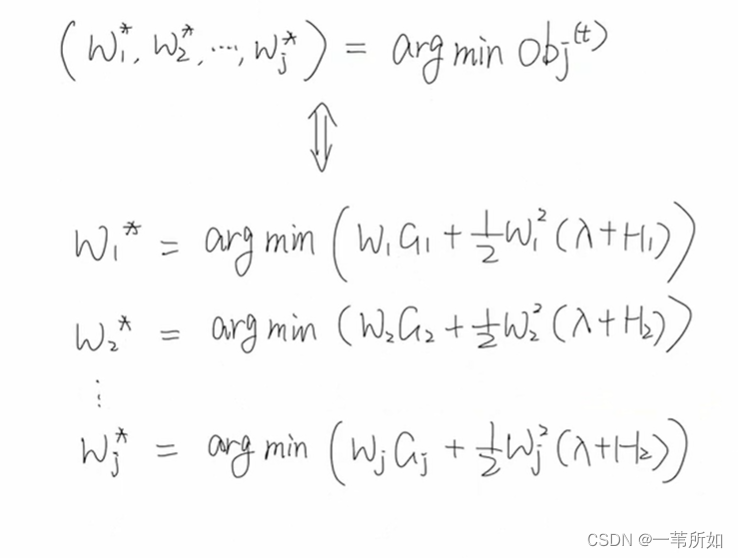
凸函數Hj為正,lambda為正
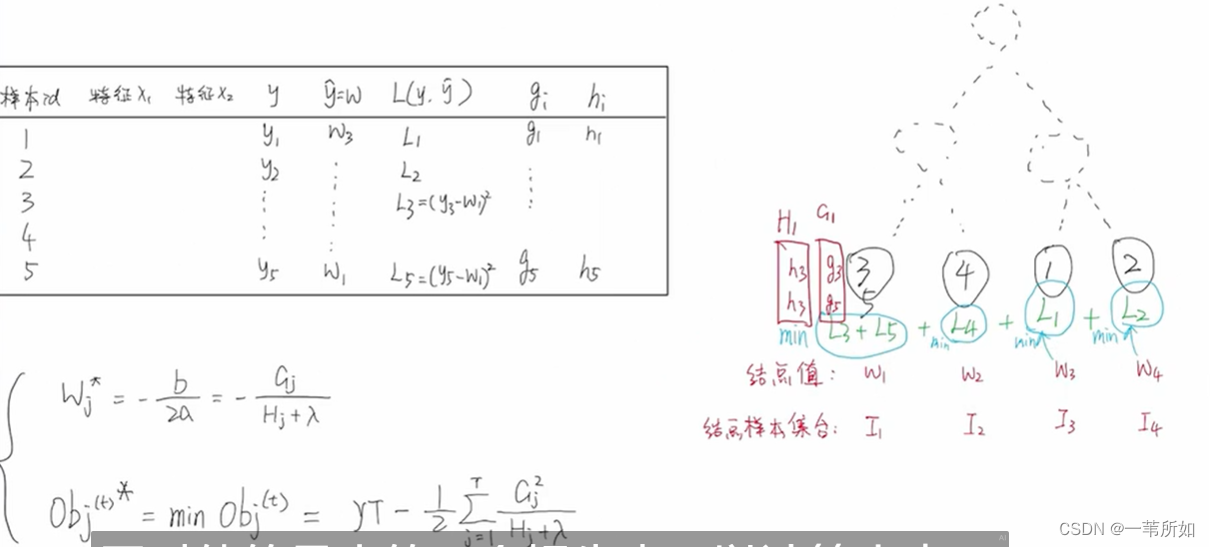
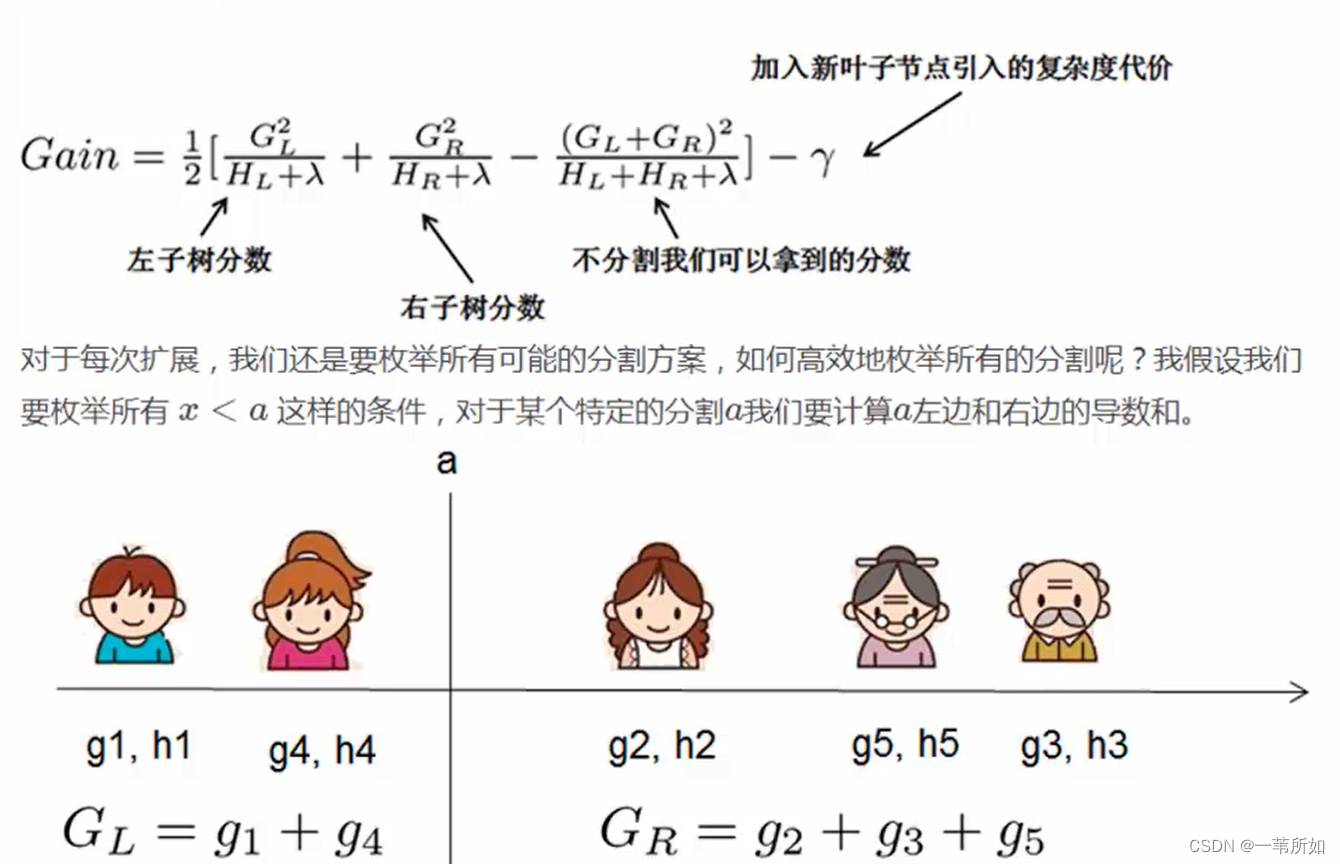
7 確定樹結構
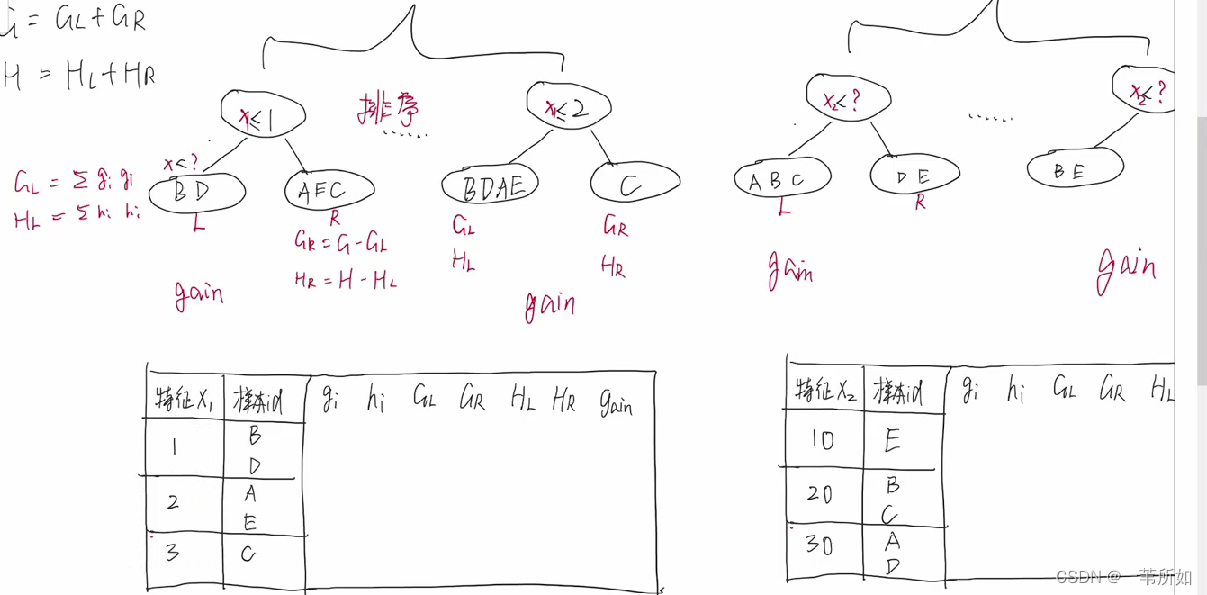
- 窮舉 – 所有組合,復雜度太高,不可行
- gain – 貪心算法
- 增益 = obj前 - obj后
不需要考慮排列組合的過程

停止分裂:
1 max(gain) <= 0
2 葉子節點個數
3 效果
作者代碼

唐宇迪
O b j ( Θ ) = L ( Θ ) + Ω ( Θ ) Obj(\Theta) = L(\Theta)+\Omega(\Theta) Obj(Θ)=L(Θ)+Ω(Θ)
損失:
L = ∑ i = 1 n l ( y i , y i ^ ) L = \sum_{i=1}^{n}{l(y_i,\hat{y_i})} \hspace{4cm} L=∑i=1n?l(yi?,yi?^?)
O b j = ∑ i = 1 n l ( y i , y i ^ ) + ∑ = 1 t Ω ( f i ) Obj= \sum_{i=1}^{n}{l(y_i,\hat{y_i})}+\sum_{=1}^{t}\Omega({f_i)} \hspace{4cm} Obj=∑i=1n?l(yi?,yi?^?)+∑=1t?Ω(fi?)

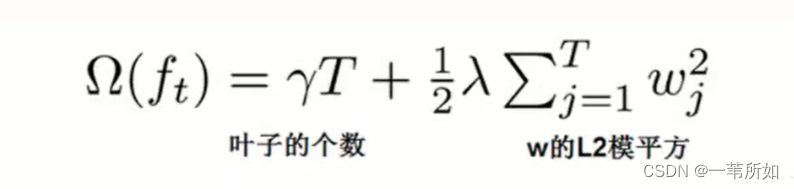

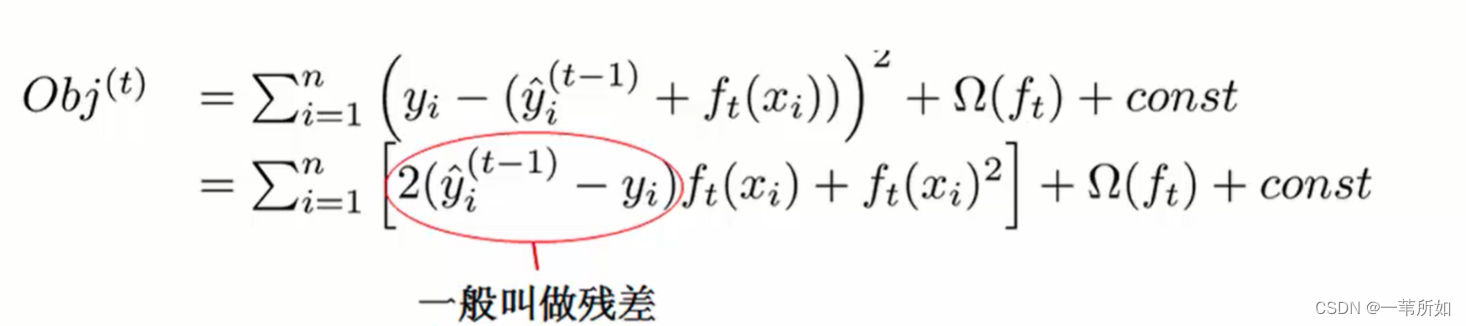
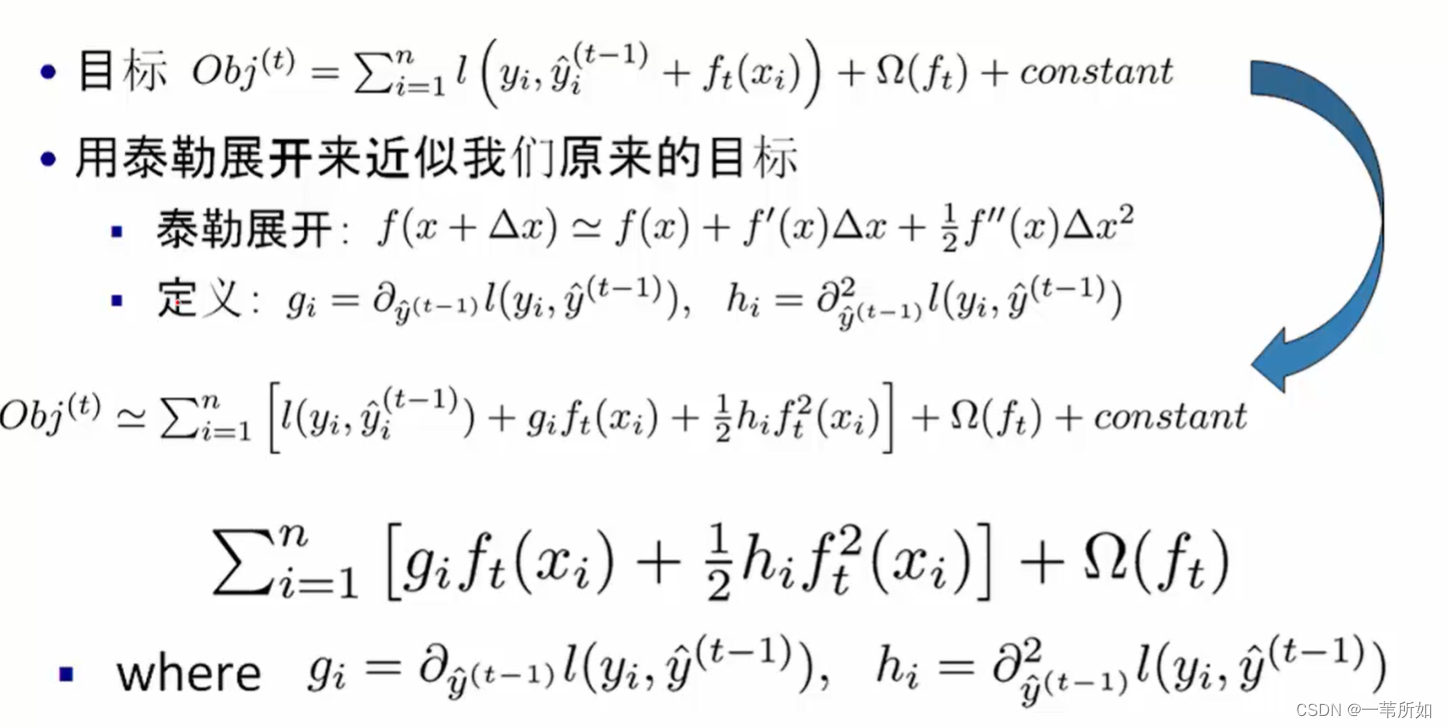
樣本的遍歷轉化為葉子節點的遍歷是等價的
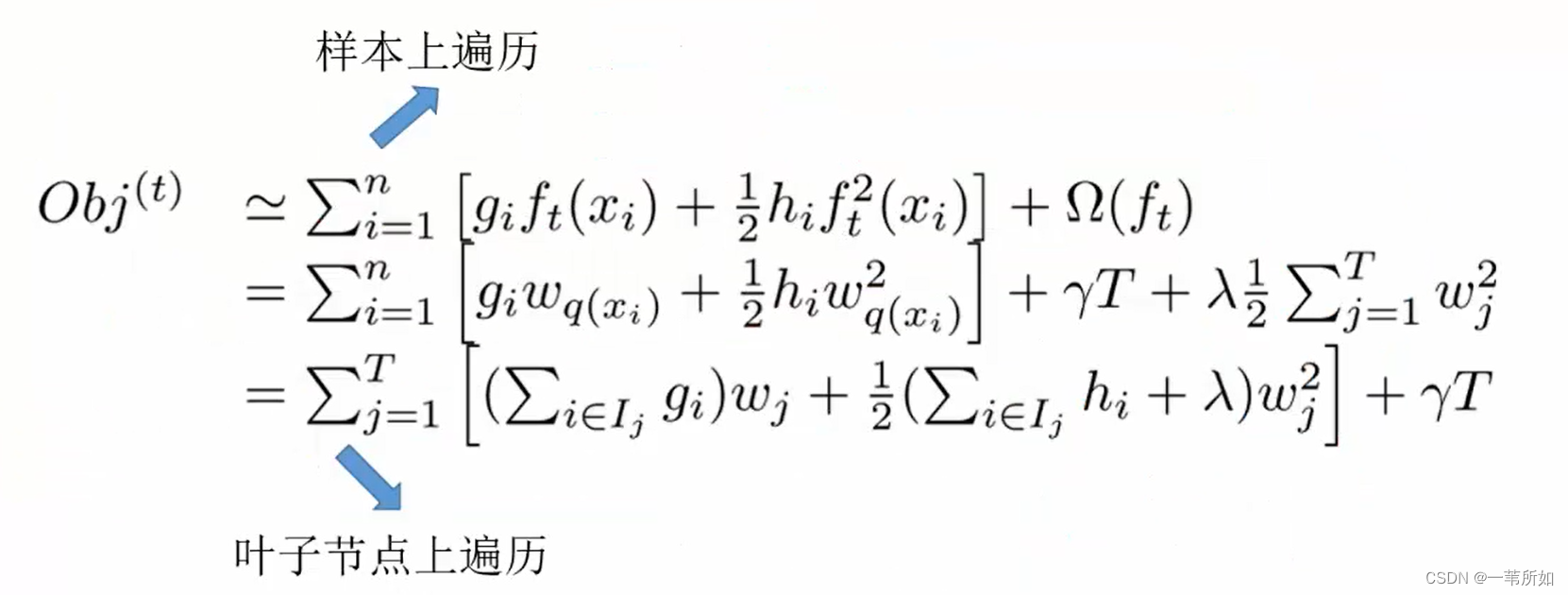
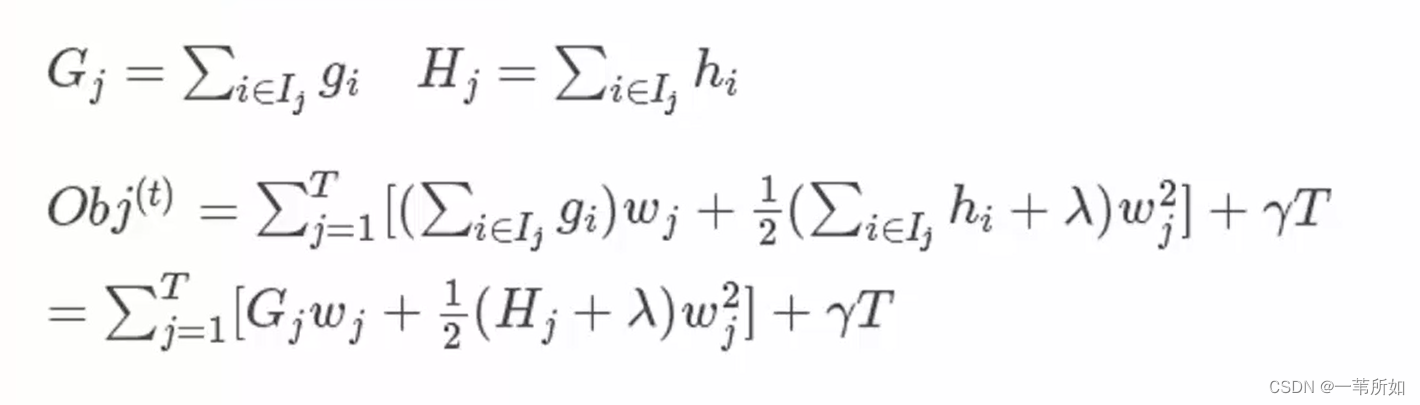


Gain
xgboost的安裝
https://www.lfd.uci.edu/~gohlke/pythonlibs/
搜索xgboost
https://www.lfd.uci.edu/~gohlke/pythonlibs/#xgboost
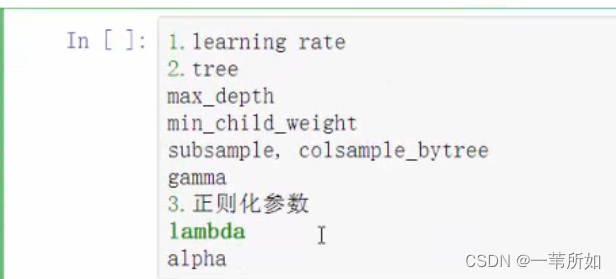
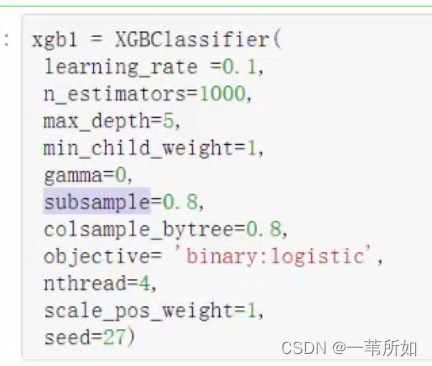
xgboost參數:
‘booster’:‘gbtree’,
‘objective’: ‘multi:softmax’, 多分類的問題
‘num_class’:10, 類別數,與 multisoftmax 并用
‘gamma’:損失下降多少才進行分裂
‘max_depth’:12, 構建樹的深度,越大越容易過擬合
‘lambda’:2, 控制模型復雜度的權重值的L2正則化項參數,參數越大,模型越不容易過擬合。
‘subsample’:0.7, 隨機采樣訓練樣本
‘colsample_bytree’:0.7, 生成樹時進行的列采樣
‘min_child_weight’:3, 孩子節點中最小的樣本權重和。如果一個葉子節點的樣本權重和小于min_child_weight則拆分過程結束
‘silent’:0 ,設置成1則沒有運行信息輸出,最好是設置為0.
‘eta’: 0.007, 如同學習率
‘seed’:1000,
‘nthread’:7, cpu 線程數

為什么xgboost要用二階泰勒展開,優勢在哪里?
xgboost進行了二階泰勒展開, 使用梯度下降求解時收斂速度更快。
引入二階泰勒展開是為了統一損失函數求導的形式,以支持自定義損失函數。二階泰勒展開可以在不選定損失函數具體形式的情況下, 僅僅依靠輸入數據的值就可以進行葉子分裂優化計算, 本質上也就把損失函數的選取和模型算法優化(參數選擇)分開了。 這種去耦合方法增加了xgboost的適用性, 使得它可以自定義損失函數, 可以用于分類, 也可以用于回歸。
————————————————
版權聲明:本文為CSDN博主「Yasin_」的原創文章,遵循CC 4.0 BY-SA版權協議,轉載請附上原文出處鏈接及本聲明。
原文鏈接:https://blog.csdn.net/Yasin0/article/details/82154768
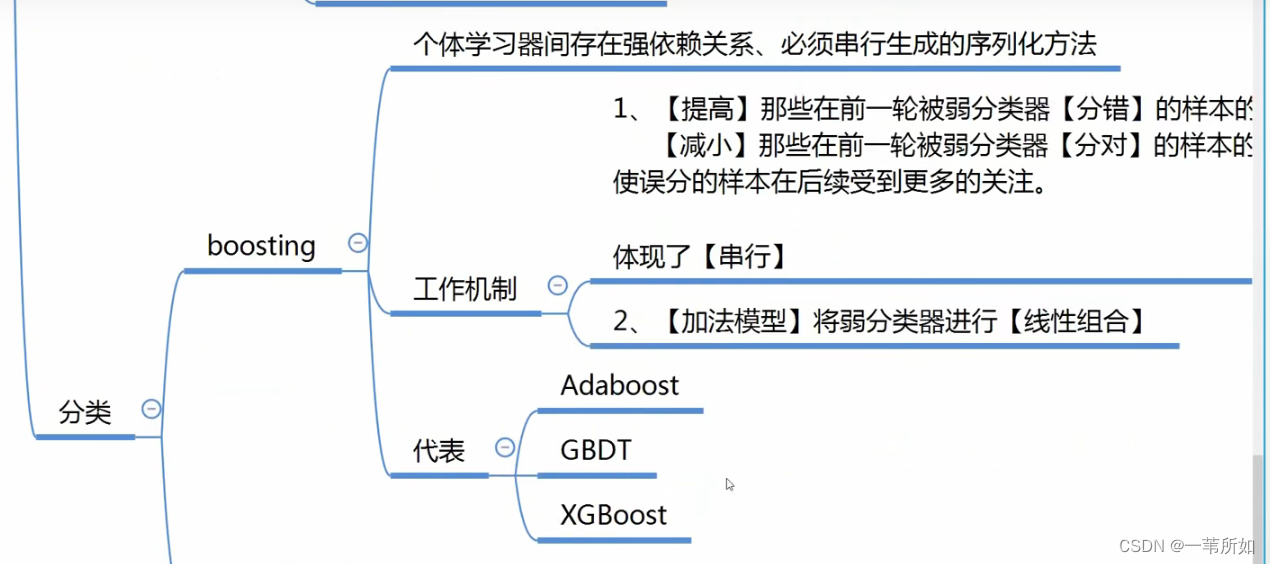
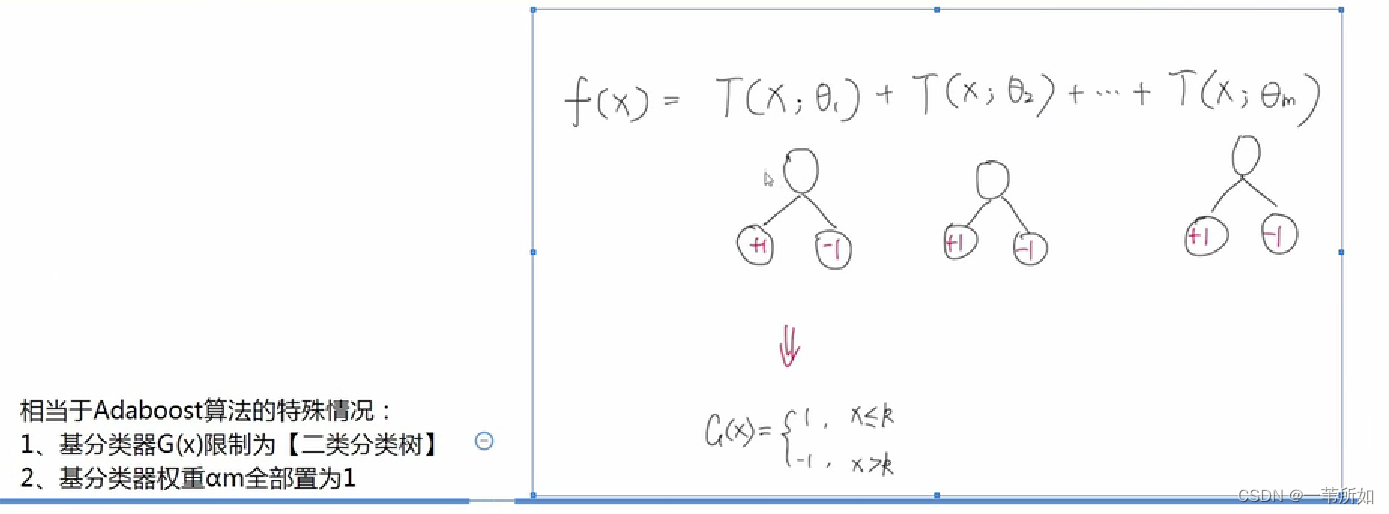
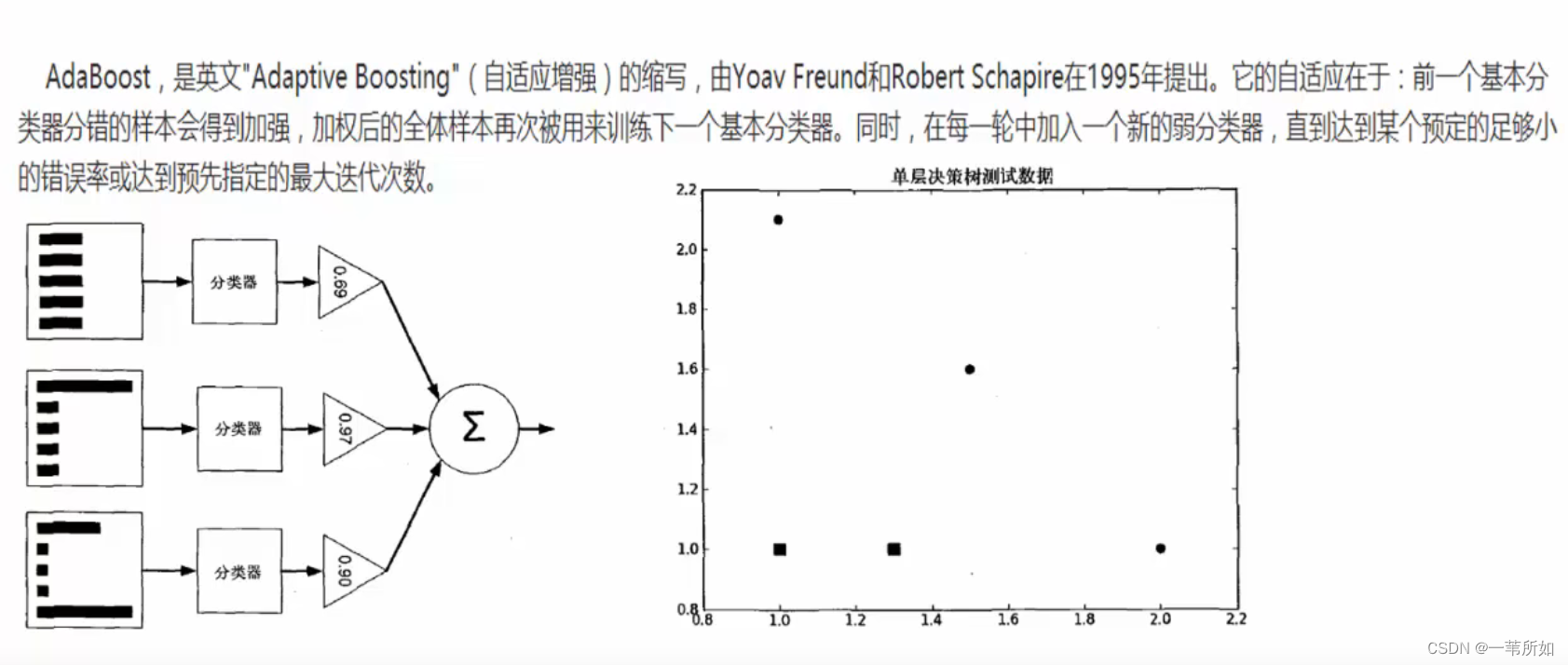
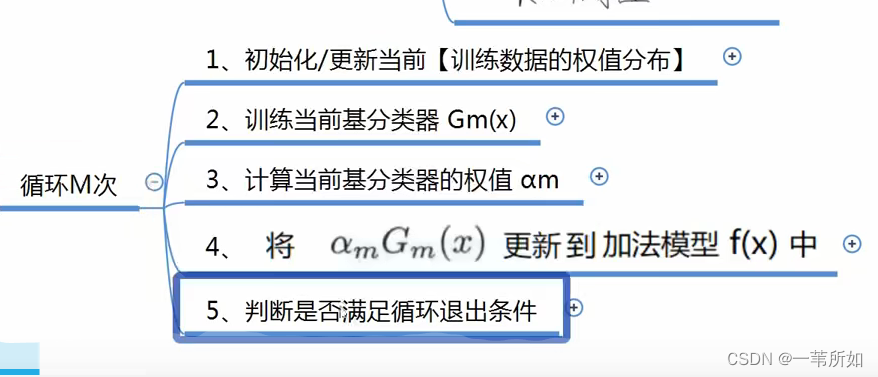
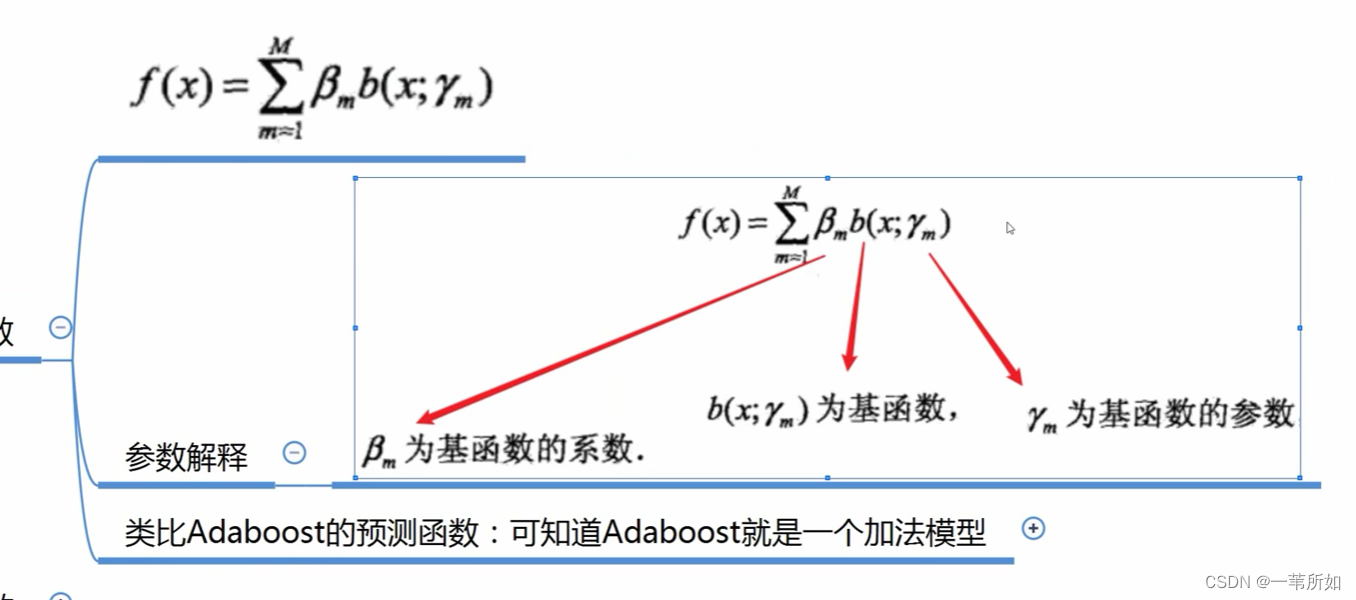
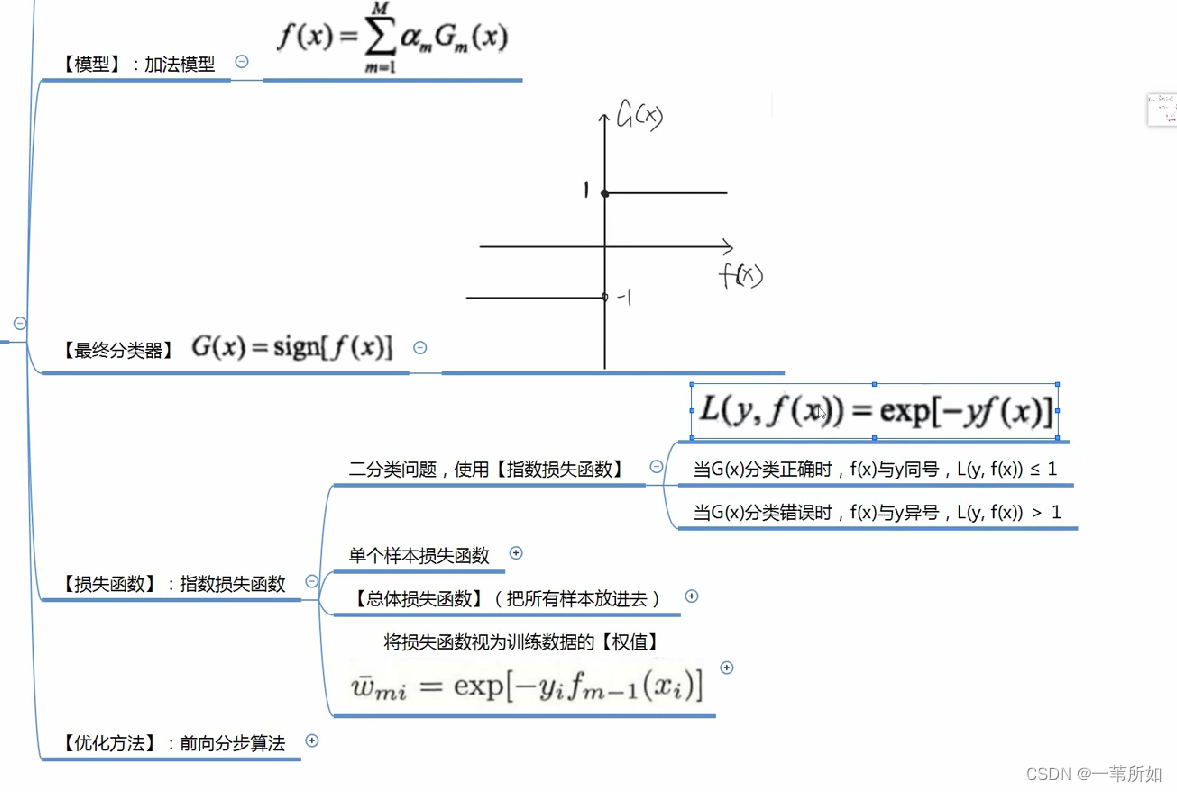
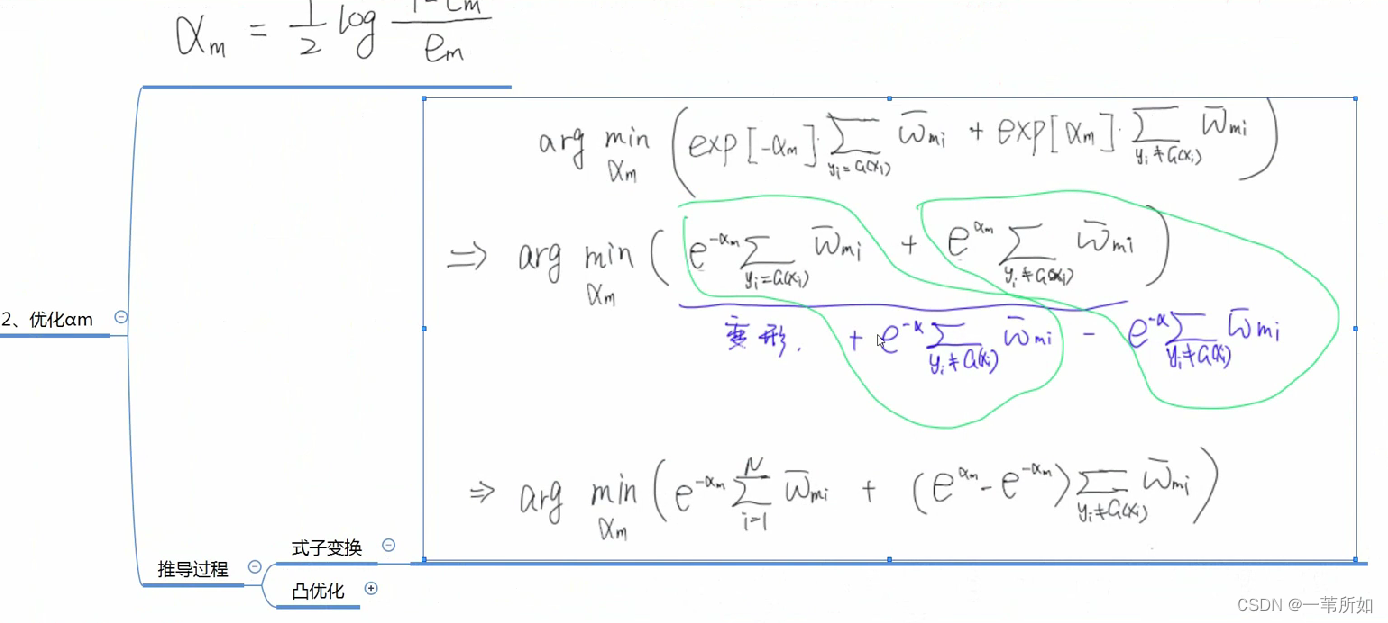
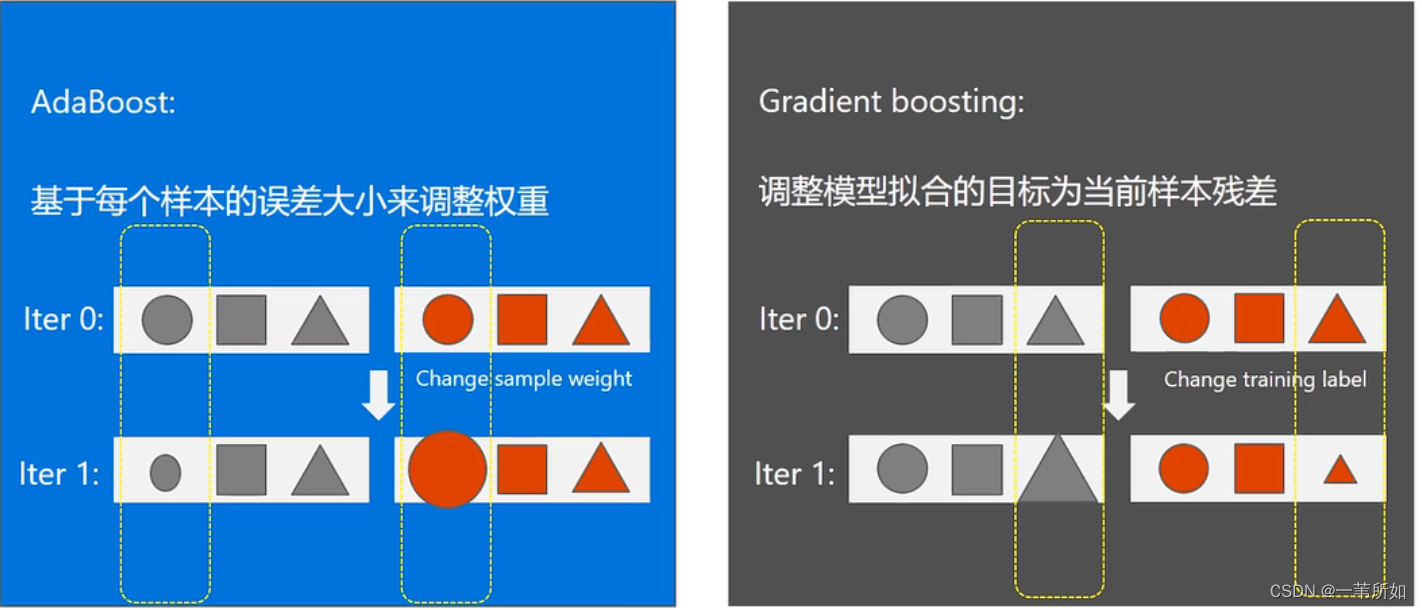
Adaboost




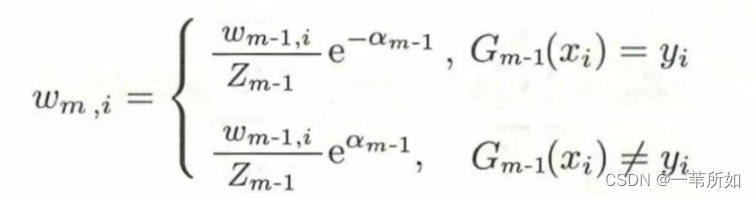



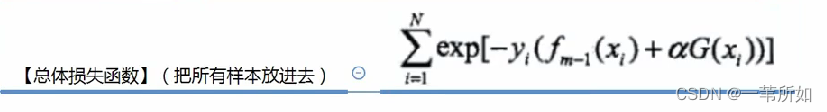




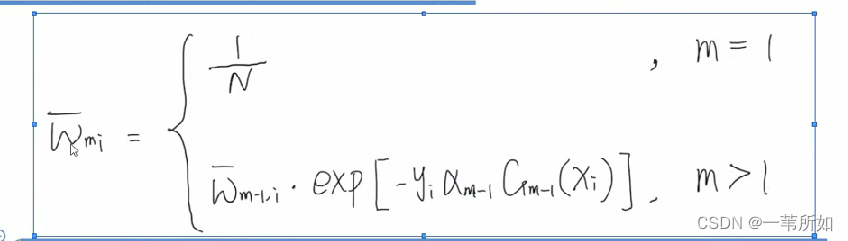

2 特征選擇
2.1
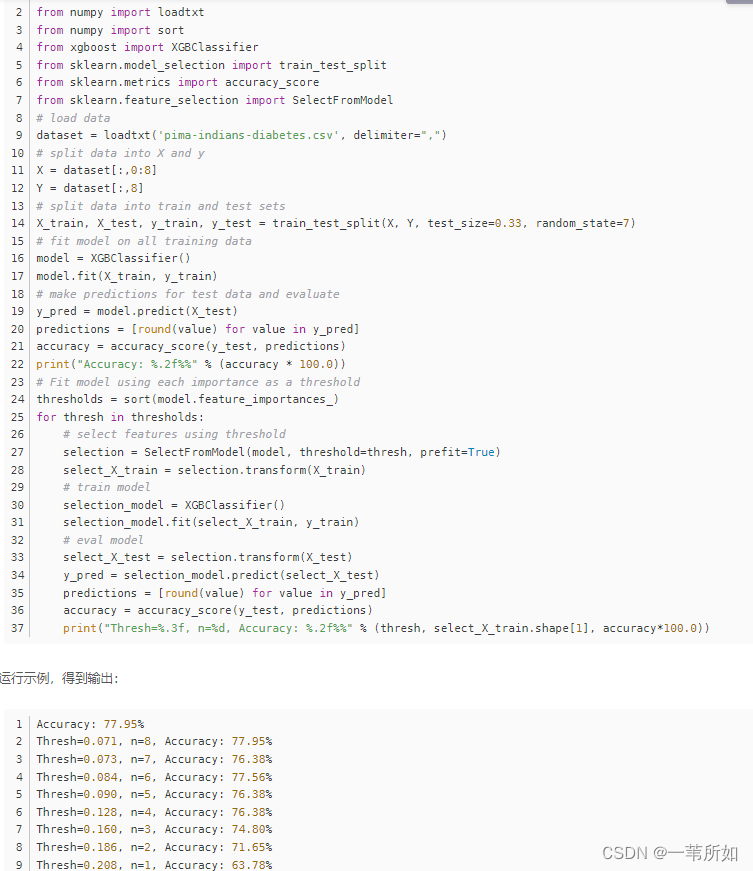
2.2 參數
1.1 weight
特征在所有樹中作為劃分屬性的次數。
1.2 gain
特征在作為劃分屬性時loss平均的降低量(也就是特征的信息增益),以特征k=1,2,…,K為例,其重要度計算可以表述如下:
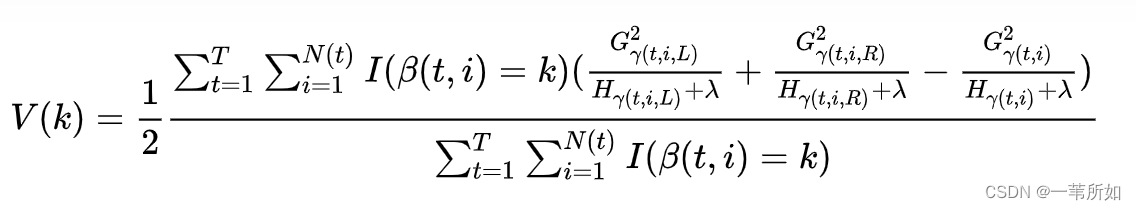
這里k表示某節點,T表示所有樹的數量,N(t)表示第t棵樹的非葉子節點數量, [公式] 表示第t棵樹的第i個非葉子節點的劃分特征,所以 [公式] ,I(.)是指示函數, [公式] 分別表示落在第t棵樹的第i個非葉子節點上所有樣本的一階導數和二階導數之和,[公式]分別表示落在第t棵樹上第i個非葉子節點的左、右節點上的一階導數之和,同理,[公式]分別表示落在第t棵樹上第i個非葉子節點的左、右節點上的二階導數之和,所以有
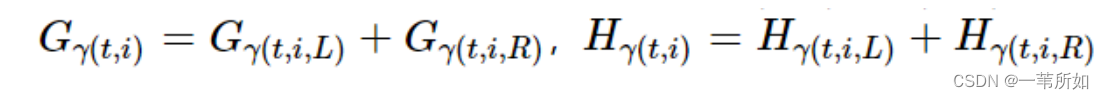
λ為正則化項的超參數。
1.3 cover
這個計算方法,需要在定義模型時定義。之后再調用model.feature_importance_得到的便是cover得到的貢獻度。
cover形象地說,就是樹模型在分裂時,特征下的葉子節點涵蓋的樣本數除以特征用來分裂的次數。分裂越靠近根部,cover值越大。比如可以定義為:特征在作為劃分屬性時對應樣本的二階導數之和的平均值:
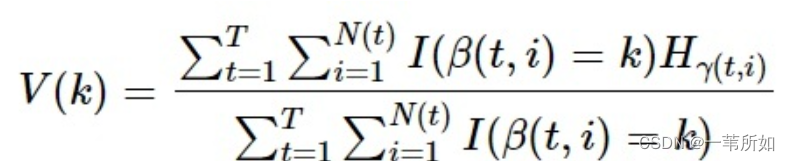
)




介紹)
)



 A~D)







)
