一、問題需求：

? ? ?迷宮尋路游戲中，有一些小怪物要攻擊主角，現在希望你給這些小怪物加上聰 明的AI (Artificial Intelligence，人工智能），讓它們可以自動繞過迷宮中的障礙物，尋找到主角的所在。

A星尋路算法 (A*search algorithm)，是一種用于尋找有效路徑的算法。

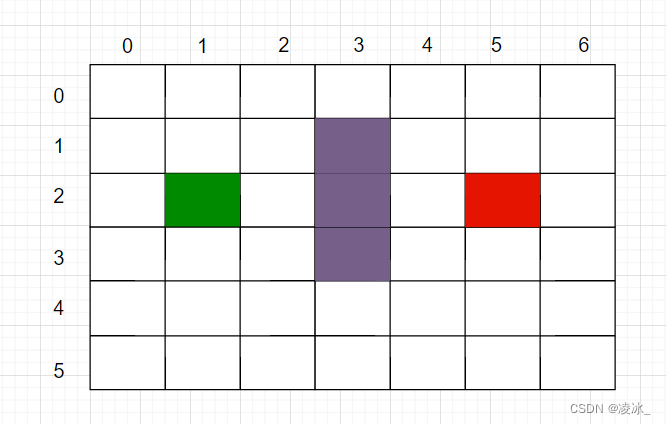
迷宮游戲的場景通常都是由小方格組成的。假設我們有一個6x7大小的迷宮

綠色的格子是起點，紅色的格子是終點，中間的3個紫色格子是一堵墻。

A星尋路算法通過計算和量化行走的各個方向的代價，來選擇最優路徑。
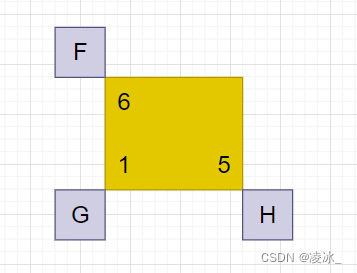
公式：F = G + H
G:從起點走到當前格子的成本，也就是已經花費了多少步。

H:在不考慮障礙的情況下，從當前格子走到目標格子的距離，也就是離目標還有多遠。

F:G和H的綜合評估，也就是從起點到達當前格子，再從當前格子到達目標格子的總步數。

每個方格都標上了?F?，?G?，?H?的值，就像起點右邊的方格那樣，左上角是?F?，左下角是?G?，右下角是?H?。

二、操作步驟：

兩個集合如下:

?open_list――可到達的格子

?close_list—―已到達的格子

第1輪尋路歷程?

第1步：把起點放入open_list可到達格子的集合。?

open_list:grid(2,1)

close_list:

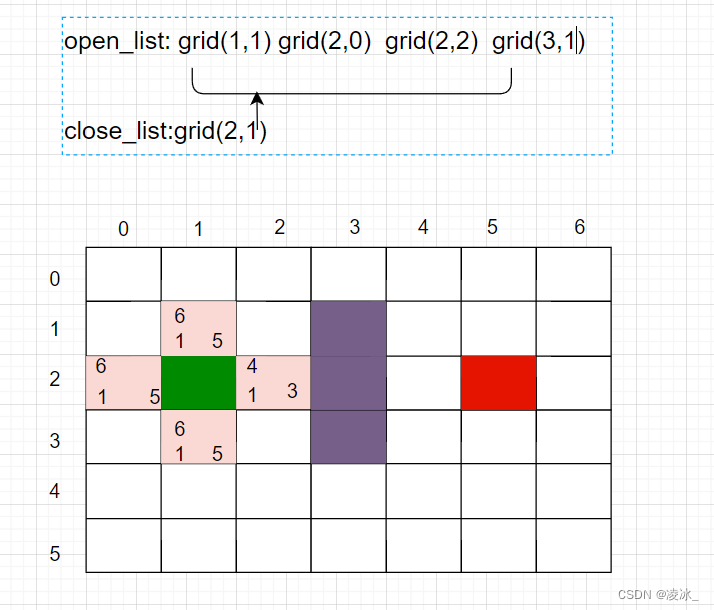
第2步：找出open_list中F值最小的方格作為當前方格。雖然我們沒有直接計算起點方格的F值，但此時open_list中只有唯一的方格grid (2，1)，把當前格子移出open_list，放入close_list。代表這個格子已到達并檢查過了。

open_list:

close_list:grid(2,1)

?

第3步：找出當前方格（剛剛檢查過的格子）上、下、左、右所有可到達的格子，看它們是否在open_list或close_list當中。如果不在，則將它們加入open_list，計算出相應的G、H、F值，并把當前格子作為它們的“父節點”。

我們需要一次又一次重復剛才的第 2步和第3步，直到找到終點為止。

第2輪尋路歷程

第1步，找出open_list中F值最小的方格，即方格grid (2，2)，將它作為當前方格，并把當前方格移出open_list，放入close_list。代表這個格子已到達并檢查過了。

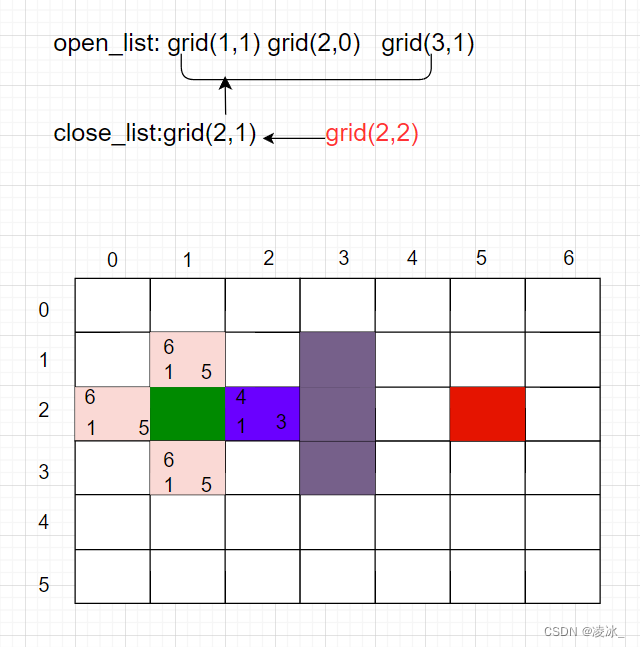
第2步，找出當前方格上、下、左、右所有可到達的格子，看它們是否在open_list或 close_list當中。如果不在，則將它們加入open_list，計算出相應的G、H、F值，并把當前格子作為它們的“父節點”。 為什么這一次open_list只增加了2個新格子呢?因為grid (2,3）是墻壁，自然不用考慮，而grid (2，1）在close_list中，說明已經檢查過了，也不用考慮。

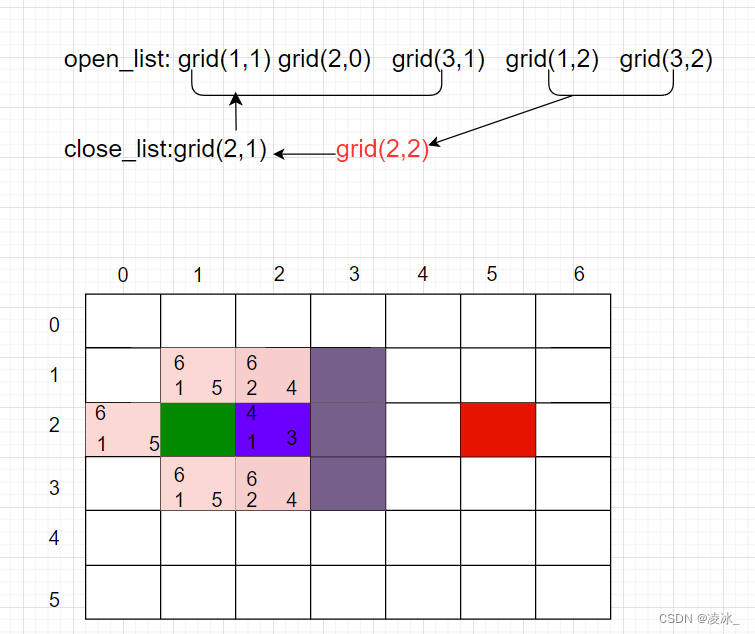
第3輪尋路歷程

第1步，找出open_list中F值最小的方格。由于此時有多個方格的F值相等，任意選擇一個即可，如將grid (2，3)作為當前方格，并把當前方格移出open_list，放入close_list。代表這個格子已到達并檢查過了。

第2步，找出當前方格上、下、左、右所有可到達的格子，看它們是否在open_list當中。如果不在，則將它們加入open_list，計算出相應的G、H、F值，并把當前格子作為它們的“父節點”。

剩下的操作就是以前面的方式繼續迭代，直到open_list中出現終點方格為止。

''''pip install colorama'''
from colorama import init, Fore, Back, Styledef a_star_search(start, end):# 初始化# 待訪問的格子open_list = []# 已訪問的格子close_list = []# 把起點加入open_listopen_list.append(start)# 主循環，每一輪檢查一個當前方格節點while len(open_list) > 0:# 在open_list中查找 F值最小的節點作為當前方格節點current_grid = find_min_gird(open_list)# 當前方格節點從openList中移除open_list.remove(current_grid)# 當前方格節點進入 closeListclose_list.append(current_grid)# 找到所有鄰近節點neighbors = find_neighbors(current_grid, open_list, close_list)for grid in neighbors:# 鄰近節點不在openList中，標記父親、G、H、F，并放入openListgrid.init_grid(current_grid, end)open_list.append(grid)# 如果終點在openList中，直接返回終點格子for grid in open_list:if (grid.x == end.x) and (grid.y == end.y):return grid# openList用盡，仍然找不到終點，說明終點不可到達，返回空return Nonedef find_min_gird(open_list=[]):# 找到openList中F值最小的節點return min(open_list, key=lambda x: x.f)def find_neighbors(grid, open_list=[], close_list=[]):grid_list = []# 上下左右四個方向if is_valid_grid(grid.x, grid.y-1, open_list, close_list):grid_list.append(Grid(grid.x, grid.y-1))if is_valid_grid(grid.x, grid.y+1, open_list, close_list):grid_list.append(Grid(grid.x, grid.y+1))if is_valid_grid(grid.x-1, grid.y, open_list, close_list):grid_list.append(Grid(grid.x-1, grid.y))if is_valid_grid(grid.x+1, grid.y, open_list, close_list):grid_list.append(Grid(grid.x+1, grid.y))return grid_listdef is_valid_grid(x, y, open_list=[], close_list=[]):# 是否超過邊界if x < 0 or x >= len(MAZE) or y < 0 or y >= len(MAZE[0]):return False# 是否有障礙物if MAZE[x][y] == 1:return False# 是否已經在open_list中if contain_grid(open_list, x, y):return False# 是否已經在closeList中if contain_grid(close_list, x, y):return Falsereturn Truedef contain_grid(grids, x, y):for grid in grids:if (grid.x == x) and (grid.y == y):return Truereturn Falseclass Grid:def __init__(self, x, y):self.x = xself.y = yself.f = 0self.g = 0self.h = 0self.parent = Nonedef init_grid(self, parent, end):self.parent = parentself.g = parent.g + 1self.h = abs(self.x - end.x) + abs(self.y - end.y)self.f = self.g + self.h# 迷宮地圖
MAZE = [[0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0]
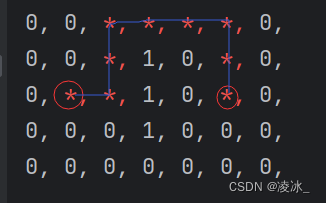
]if __name__ == '__main__':# 設置起點和終點start_grid = Grid(2, 1)# end_grid = Grid(2, 5)end_grid = Grid(3, 4)# 搜索迷宮終點result_grid = a_star_search(start_grid, end_grid)# 回溯迷宮路徑path = []while result_grid is not None:path.append(Grid(result_grid.x, result_grid.y))result_grid = result_grid.parent# 輸出迷宮和路徑，路徑用星號表示for i in range(0, len(MAZE)):for j in range(0, len(MAZE[0])):if contain_grid(path, i, j):print(Fore.RED + "*, "+Fore.RESET, end='')else:print(str(MAZE[i][j]) + ", ", end='')print()

? ? ??