這是我的第287篇原創文章。
一、引言
? ? ? 主成分分析（Principal Component Analysis, PCA）是一種常用的降維技術，它通過線性變換將原始特征轉換為一組線性不相關的新特征，稱為主成分，以便更好地表達數據的方差。
? ? ? 在特征重要性分析中，PCA 可以用于理解數據中最能解釋方差的特征，并幫助識別對目標變量影響最大的特征。可以通過查看PCA的主成分（主特征向量）以及各主成分所對應的特征重要性來推斷哪些原始特征在新特征中起到了較大影響。
? ? ? PCA 的局限性：
- PCA 是一種線性變換方法，可能無法很好地處理非線性關系的數據。
- PCA 可能會丟失一些信息，因為它主要關注的是數據中的方差，而忽略了其他方面的信
- PCA 假設主成分與原始特征之間是線性關系，這在某些情況下可能不成立。
二、實現過程
2.1 讀取數據
# 準備數據
data = pd.read_csv(r'dataset.csv')
df = pd.DataFrame(data)
print(df)
# 目標變量和特征變量
target = 'target'
features = df.columns.drop(target)
# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(df[features], df[target], test_size=0.2, random_state=0)df：
2.2 對訓練集做PCA主成分分析
自主選擇主成分，并打印出每個主成分的解釋性方差：
pca = PCA(n_components='mle')
pca.fit(X_train)
var_ratio = pca.explained_variance_ratio_
for idx, val in enumerate(var_ratio, 1):print("Principle component %d: %.2f%%" % (idx, val * 100))
print("total: %.2f%%" % np.sum(var_ratio * 100))結果：
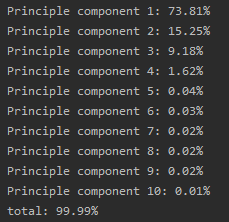
共計10個主成分。
2.3 通過主成分分析原始特征重要性
打印出每個特征對于主成分的系數，這反映了原始特征的重要性：
print(pca.components_)結果：
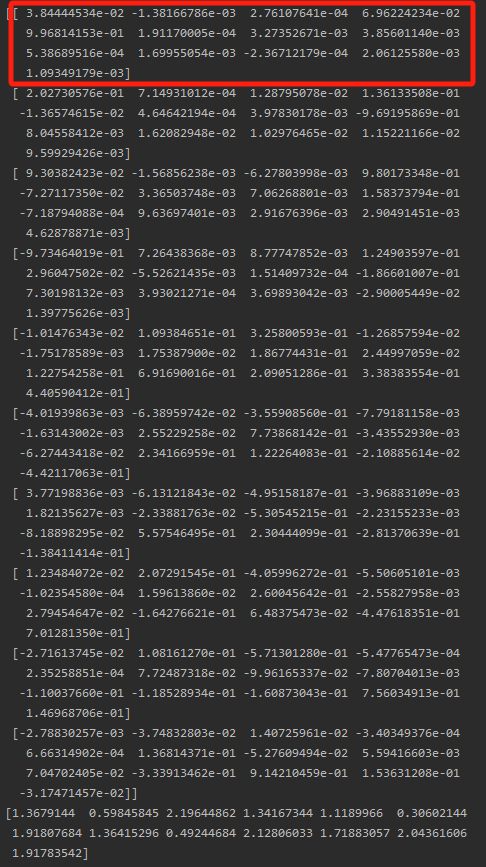
通過計算10個主成分中，每個原始特征的系數絕對值之和作為該特征的最終貢獻度：
# 計算原始特征與主成分的相關性（絕對值）
feature_importance?=?np.abs(pca.components_)
# 計算每個主成分中原始特征的權重（系數）和
feature_importance_sum?=?np.sum(feature_importance,?axis=0)
# 打印原始特征的重要性（貢獻度）
print("\n原始特征的重要性（貢獻度）:")
ranking_df?=?pd.DataFrame({'特征':?features,?'貢獻度':?feature_importance_sum})
ranking_df = ranking_df.sort_values(by='貢獻度')
print(ranking_df)結果：
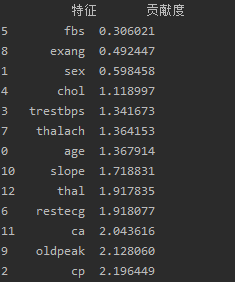
可視化：
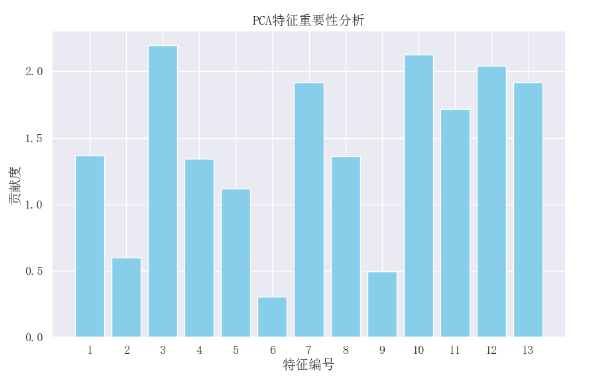
2.4 查看累計解釋方差比率與主成分個數的關系
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.arange(1, len(var_ratio) + 1), np.cumsum(var_ratio), "-ro")
ax.set_title("Cumulative Explained Variance Ratio", fontsize=15)
ax.set_xlabel("number of components")
ax.set_ylabel("explained variance ratio(%)")
plt.show()結果：
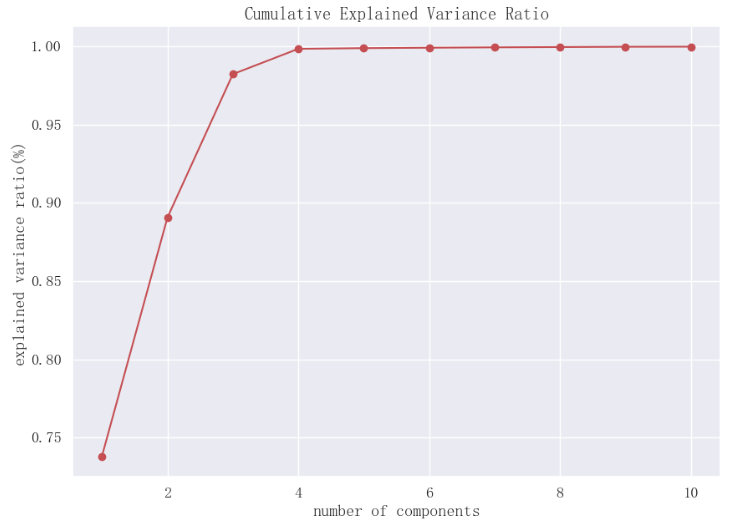
前2個主成分累計解釋性方差比率接近0.9，前3個主成分累計解釋方差比率超過0.95。
2.5 自動選擇最優的主成分個數
設定累計解釋方差比率的目標，讓sklearn自動選擇最優的主成分個數：
target = 0.9 # 保留原始數據集90%的變異
res = PCA(n_components=target).fit_transform(X_train)
print("original shape: ", X_train.shape)
print("transformed shape: ", res.shape)結果：
選擇了3個主成分。
2.6 主成分選擇可視化（以2個主成分為例）
選擇兩個主成分，并進行可視化：
pca=PCA(n_components=2) #加載PCA算法，設置降維后主成分數目為2
reduced_x=pca.fit_transform(X_train)#對樣本進行降維
principalDf = pd.DataFrame(data = reduced_x, columns = ['principal component 1', 'principal component 2'])
print(principalDf)
y_train = np.array(y_train)
yes_x,yes_y=[],[]
no_x,no_y=[],[]
for i in range(len(reduced_x)):if y_train[i] ==1:yes_x.append(reduced_x[i][0])yes_y.append(reduced_x[i][1])elif y_train[i]==0:no_x.append(reduced_x[i][0])no_y.append(reduced_x[i][1])
plt.scatter(yes_x,yes_y,c='r',marker='x')
plt.scatter(no_x,no_y,c='b',marker='D')
plt.xlabel("First Main Component")
plt.ylabel("Second Main Component")
plt.show()結果：
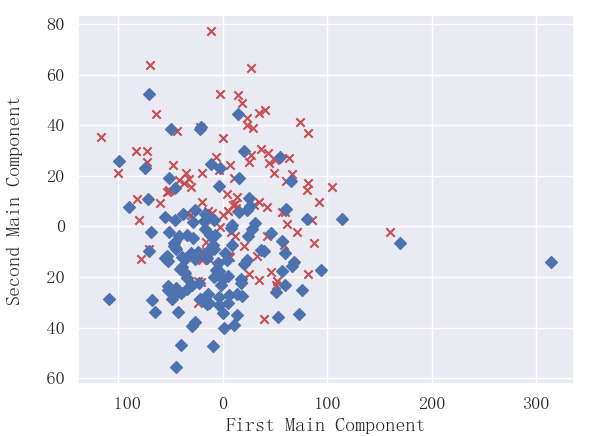
可以看出2個主成分可以大概劃分出兩類。
作者簡介：
讀研期間發表6篇SCI數據挖掘相關論文，現在某研究院從事數據算法相關科研工作，結合自身科研實踐經歷不定期分享關于Python、機器學習、深度學習、人工智能系列基礎知識與應用案例。致力于只做原創，以最簡單的方式理解和學習，關注我一起交流成長。需要數據集和源碼的小伙伴可以關注底部公眾號添加作者微信。
)
)
