1. 簡介

網格會影響仿真的準確性和速度，花時間理解網格化過程是很重要的。

CST 中可用的數值方法包括FIT、TLM、FEM、MoM，使用不同類型的網格：

FIT和TLM：六面體

FEM：四面體、平面

MoM：表面

CFD：八叉樹

CST六面體網格： 通常，六面體網格不符合材料的突變；請注意，這并不是必需的，因為CST提供了完美邊界近似（PBA）和薄板技術（TST），與FIT方法結合使用在六面體網格上。 TLM求解器提供了一個非常高效的基于八叉樹的網格化算法，這大大減少了總的單元數量。 無論是FIT還是TLM六面體網格化都非常穩健，即使是對于最復雜的導入幾何體。

CST四面體和表面網格： 符合實體邊界，因此符合材料的突變。 自適應網格細化方案可以有效地應用于非結構化網格。 請注意，使用四面體網格可能需要特別注意：有時CAD模型的不準確性最終會在網格中顯現出來。在極少數情況下，這種不準確性甚至可能中斷網格生成。在這些情況下，CST網格生成器會提供關于網格化結果的廣泛反饋。

通過比較驗證： 在許多情況下，對于同一個問題使用不同的網格是有益的。結果的比較為您的數值結果提供了額外的有效性檢查。 請注意，這不是一個耗時的任務。與使用不同的軟件工具進行驗證相比，可以在同一CST軟件中使用不同的求解方法，而無需再次設置計算模型！

2. 網格介紹

2.1?六面體網格

• 六面體網格通常不符合材料的突變，但這并不是必需的，因為CST提供了完美邊界近似（PBA）和薄板技術（TST），與有限積分法（FIT）方法結合使用在六面體網格上。
• TLM求解器提供了一個基于八叉樹的高效網格化算法，這可以大幅減少總的單元數量。
• FIT和TLM六面體網格化對于最復雜的導入幾何體都非常穩健。

2.2?四面體和表面網格

• 四面體和表面網格符合實體邊界，因此也符合材料的突變。
• 自適應網格細化方案可以有效地應用于非結構化網格。
• 使用四面體網格時需要特別注意，有時CAD模型的不準確性最終會在網格中顯現出來。在極少數情況下，這種不準確性甚至可能中斷網格生成。在這些情況下，CST網格生成器會提供關于網格化結果的廣泛反饋。

2.3 嘗試對比

• 在許多情況下，對于同一個問題使用不同的網格是有益的。結果的比較為您的數值結果提供了額外的有效性檢查。
• 對比操作并不耗時。與使用不同的軟件工具進行驗證相比，可以在同一CST軟件中使用不同的求解方法，而無需再次設置計算模型。

3. PBA 介紹

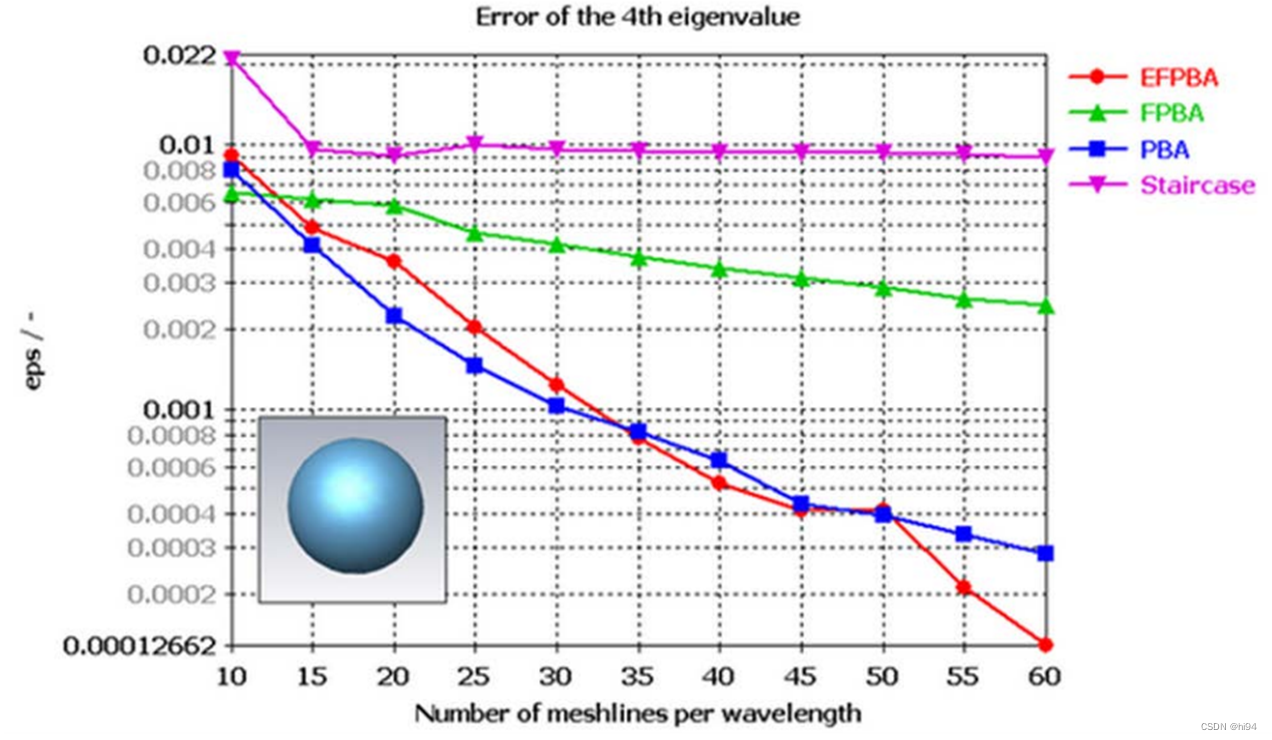
CST軟件中不同技術在計算第四個特征值誤差時的表現。

橫軸：波長的網格線數量。

縱軸：特征值誤差（eps）。

以下是圖中四種技術的詳細分析：

Staircase（階梯法）

• 從圖中可以看出，Staircase方法的誤差隨著網格線數量的增加變化不大，始終保持在一個較高的水平，大約在0.01到0.02之間。
• 這種方法誤差較大，即使增加網格線數量，精度也不會明顯提高。

FPBA – Fast Perfect Boundary Approximation（快速完美邊界近似）

• FPBA方法的誤差隨著網格線數量的增加而逐漸減小，但減小幅度較慢。
• 在網格線數量較多時，誤差降低到0.001左右，但相比其他方法，精度提升不明顯。

PBA – Perfect Boundary Approximation（完美邊界近似）

• PBA方法在增加網格線數量時，誤差顯著減小。
• 在網格線數量超過40時，誤差已經低于0.0003，說明此方法精度較高。

EFPBA – Enhanced Accuracy FPBA（增強精度的快速完美邊界近似）

• EFPBA方法的誤差隨著網格線數量的增加迅速減小。
• 在網格線數量達到60時，誤差低于0.0002，是四種方法中精度最高的。
• 顯示出EFPBA在提高計算精度方面的顯著優勢。

EFPBA在精度上表現最佳，其次是PBA，然后是FPBA，而Staircase方法的精度最差。

4. 總結

在CST仿真中，網格化是影響準確性和速度的關鍵因素。六面體網格雖不符合材料突變，但PBA和TST技術使其與FIT和TLM方法結合得以優化。四面體和表面網格則自然符合邊界，適用于自適應細化。對比不同網格的結果可增強數值結果的有效性。特別是，EFPBA技術在計算精度上表現卓越，隨網格線數量增加，誤差顯著降低，遠超其他方法，是提高仿真精度的首選技術。