DS高階：跳表

一、skiplist

1.1?skiplist的概念

? ? ? ? skiplist本質上也是一種查找結構，用于解決算法中的查找問題，跟平衡搜索樹和哈希表的價值是一樣的，可以作為key或者key/value的查找模型。skiplist是由William Pugh發明的，最早出現于他在1990年發表的論文《Skip Lists: A Probabilistic Alternative to Balanced Trees》?

? ? ? ? skiplist，顧名思義，首先它是一個list。實際上，它是在有序鏈表的基礎上發展起來的。如果是一個有序的鏈表，查找數據的時間復雜度是O(N)。

1.2?skiplist的優化思路分析

? ? ? ? ? ?假如我們每相鄰兩個節點升高一層，增加一個指針，讓指針指向下下個節點，如下圖b所
示。這樣所有新增加的指針連成了一個新的鏈表，但它包含的節點個數只有原來的一半。由于新增加的指針，我們不再需要與鏈表中每個節點逐個進行比較了，需要比較的節點數大概只有原來的一半。（多層鏈表的啟發思路）以此類推，我們可以在第二層新產生的鏈表上，繼續為每相鄰的兩個節點升高一層，增加一個指針，從而產生第三層鏈表。如下圖c，這樣搜索效率就進一步提高了。

? ? ? ?skiplist正是受這種多層鏈表的想法的啟發而設計出來的。實際上，按照上面生成鏈表的方式，上面每一層鏈表的節點個數，是下面一層的節點個數的一半，這樣查找過程就非常類似二分查找，使得查找的時間復雜度可以降低到O(log n)。但是這個結構在插入刪除數據的時候有很大的問題，插入或者刪除一個節點之后，就會打亂上下相鄰兩層鏈表上節點個數嚴格的2:1的對應關系。如果要維持這種對應關系，就必須把新插入的節點后面的所有節點（也包括新插入的節點）重新進行調整，這會讓時間復雜度重新蛻化成O(n)。

? ? ? ?skiplist的設計為了避免這種問題，做了一個大膽的處理，不再嚴格要求對應比例關系，而是
插入一個節點的時候隨機出一個層數。這樣每次插入和刪除都不需要考慮其他節點的層數，這樣就好處理多了。

?1.3 隨機出層數的含義

? ? ? ? ?插入節點時隨機出一個層數究竟是什么意思呢？？？難道直接random任意數就可以了嗎？？

答：雖然是隨機，但是也有規則的限制。這里首先要細節分析的是這個隨機層數是怎么來的。一般跳表會設計一個最大層數maxLevel的限制，其次會設置一個多增加一層的概率p。那么計算這個隨機層數的偽代碼如下圖：

?一個節點的平均層數（也即包含的平均指針數目），計算如下：

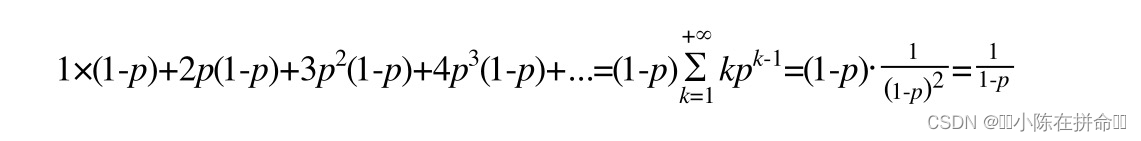
現在很容易計算出：
當p=1/2時，每個節點所包含的平均指針數目為2；
當p=1/4時，每個節點所包含的平均指針數目為1.33。

時間復雜度：logN

具體的分析可以看下面的文章：Redis內部數據結構詳解(6)——skiplist
?

2、skiplist的模擬實現

力扣有一道設計跳表的題. - 力扣（LeetCode）設計跳表

基本的調表需要實現4個函數：構造函數、搜索、插入、刪除。下面我們來一個個分析。

2.1?skiplist的基本結構

struct SkiplistNode
{int _val;//存儲對應的值vector<SkiplistNode*> _nextV;//存放對應的next指針集合SkiplistNode(const int&val, size_t level = 1) //level表示需要開辟的層數 不傳就是默認開滿:_val(val){_nextV.resize(level, nullptr);}
};class Skiplist
{typedef  SkiplistNode Node;
public:private:Node* _head;//虛擬頭節點const size_t _maxLevel = 32; //用缺省參數去初始化const double _p = 0.25;//用缺省參數去初始化
};

?2.2?skiplist的默認構造

Skiplist()
{srand((unsigned int)time(nullptr));//為了方便后面的隨機取層數,先弄一個隨機種子_head = new Node(-1);//默認開一層，用默認構造初始化
}

? ? ? ? 給虛擬頭節點申請一塊空間，一開始默認就開一層。為了能夠方面后面利用rand函數隨機取層數，所以在這個地方先用了一個時間種子

? ? ? ? ?我們默認開的是一層，因為在數據量小的時候其實我們可以根據插入的情況去調整_head的層數，如果是數據量特別大的話，也可以一次性就把他開到滿

2.3?skiplist的搜索

bool search(int target) 
{//要不斷往下走Node* cur = _head;int level = _head->_nextV.size() - 1;//從后往前去找while (level >= 0){//如果我比你大 我就跳過去->更新cur   //如果我比你小或者你為空 我就往下走 --levelif (cur->_nextV[level] == nullptr || target < cur->_nextV[level]->_val) --level;else if (target > cur->_nextV[level]->_val)  cur = cur->_nextV[level];else return true;}return false; //循環結束都沒有找到，說明找不到。
}

我們要從高層一直找到底層，所以要從_nextV的后面開始找。

1、如果你為空，或者我比你小，那就得往下走 ->--level

2、如果我比你大，就可以直接跳到你的位置->更新cur=cur->_nextV[level]

3、如果找到了就返回true，如果循環結束了都找不到，那就返回false

2.4 找到prevV指針數組

為什么要單獨去封裝這個函數呢？

? ? ? ? ?因為不管是插入，還是刪除，我們都需要去找前驅節點的集合，這樣才能去改變連接關系，所以為了提高代碼的復用性，封裝這樣的一個函數，去找到待插入位置或者是待刪除位置的前驅節點集合。

vector<Node*> FindPrevNode(int num) //幫助我們找到前驅指針集合
{//最終我們要返回待插入位置或者是待刪除位置的前驅指針集合  一開始的時候默認是head、Node* cur = _head;int level = _head->_nextV.size() - 1;vector<Node*> prevV(level+1, _head);while (level >= 0){if (cur->_nextV[level] == nullptr || num < cur->_nextV[level]->_val){//更新level的層的前一個節點 往下跳之前保存前驅節點prevV[level] = cur;--level;}else//(num >= cur->_nextV[level]->_val)  cur = cur->_nextV[level];}return prevV;
}

? ? ? ? 當我們需要往后面跳之前，保存當前的cur進去prevV數組中，這樣我們返回的數組就是待插入節點對應的前驅節點集合了！

2.5 隨機層數的生成函數

? ? ? 我們在插入節點之前，要隨機生成一個層數，所以要先實現一個生成層數的函數

2.5.1 C語言rand( )版本

size_t RandomLevel() //C語言版本
{size_t level = 1;//初始的層數while (rand() <= RAND_MAX * _p && level < _maxLevel)  ++level; //RAND_MAX是隨機數的最大值return level;
}

2.5.2 C++11隨機數庫

	size_t RandomLevel() //需要的時候去搜 C++11的隨機數庫即可  頭文件chrono和random{//類似隨機數種子，但是只用一次是最好的 所以設置成staic 這樣就只會調用一次了static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());//now.time_since_epoch().count()是一個時間戳 類似隨機數種子static std::uniform_real_distribution<double> distribution(0.0, 1.0);size_t level = 1;while (distribution(generator) <= _p && level < _maxLevel)  ++level;return level;}

? ? ? ? ?std::chrono::system_clock::now().time_since_epoch().count() 類似一個時間戳，相當于是隨機種子，但是由于只需要初始化一次，所以我們將他變成static變量，這樣就只要初始化一次即可！

? ? ? ? 關于C++11的random庫用法，還是比較復雜的，大家可以參考一些相關的文章。

2.6?skiplist的增加

void add(int num)  //插入節點
{vector<Node*> prevV = FindPrevNode(num); //右值引用size_t n = RandomLevel(); //表示需要開多少層//如果n超過了_head的最大層數，那么就要調整一下if (n > _head->_nextV.size()){_head->_nextV.resize(n, nullptr); prevV.resize(n, _head);//不夠的地方也要更新過去}Node* newnode = new Node(num, n);//申請對應的新節點  然后根據prevV數組去建立連接for (size_t i = 0; i < n; ++i) //連接前后節點，首先要先連后面的 再連前面的{newnode->_nextV[i] = prevV[i]->_nextV[i];prevV[i]->_nextV[i] = newnode;}
}

? ? ? ? ?一個很關鍵的地方就是，我們隨機生成了一個層數后，有可能我們的_head的層數都沒這個多，所以我們必須利用resize去初始化一下，否則會出現越界訪問。?

? ? ? ? ?中間插入的邏輯就類似鏈表的指定位置插入，先讓自己的后繼指向前驅的后繼，然后再讓前驅指向自己，必須按照這個順序，否則會丟失節點

2.7?skiplist的刪除

bool erase(int num) 
{//首先 有可能沒有這個數 所以要看看是不是真的沒有vector<Node*> prevV = FindPrevNode(num);if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num)  return false;//有的話，就要去刪除然后重新連接Node* del = prevV[0]->_nextV[0];//我們需要刪除的節點，但是在刪除前要調整一下連接的關系for (size_t i = 0; i < del->_nextV.size(); ++i)  prevV[i]->_nextV[i] = del->_nextV[i];delete del;// 如果刪除最高層節點，把頭節點的層數也降一下int i = _head->_nextV.size() - 1;while (i >= 0){if (_head->_nextV[i] == nullptr)  --i;else  break;}_head->_nextV.resize(i + 1);return true;
}

? ? ?有可能我們找不到這個數，這個時候就沒什么可以刪的了。

? ? ? 在刪除這個節點之前，我們要先記錄這個節點，然后去改變被刪除節點的連接關系，類似鏈表的指定位置刪除。

? ? ? 如果我們刪除的恰好是最高層的節點，這個時候可以整體對頭結點的層數降個高度，這樣就提高了查找效率。