【C++】AVL

提示：文章寫完后，目錄可以自動生成，如何生成可參考右邊的幫助文檔

前言

一、AVL 樹

1.1、AVL樹的概念

1.2、AVL樹節點的定義

1.3、AVL樹的插入

1.4、AVL樹的旋轉

1.4.1、新節點插入較高左子樹的左側---左左：右單旋

1.4.2、新節點插入較高右子樹的右側---右右：左單旋

1.4.3、新節點插入較高左子樹的右側---左右：先左單旋再右單旋

1.4.4、新節點插入較高右子樹的左側---右左：先右單旋再左單旋

1.5、AVL樹的驗證

總結

前言

世上有兩種耀眼的光芒，一種是正在升起的太陽，一種是正在努力學習編程的你!一個愛學編程的人。各位看官，我衷心的希望這篇博客能對你們有所幫助，同時也希望各位看官能對我的文章給與點評，希望我們能夠攜手共同促進進步，在編程的道路上越走越遠！

提示：以下是本篇文章正文內容，下面案例可供參考

一、AVL 樹

1.1、AVL樹的概念

二叉搜索樹雖可以縮短查找的效率，但如果數據有序或接近有序二叉搜索樹將退化為單支樹，查找元素相當于在順序表中搜索元素，效率低下。因此，兩位俄羅斯的數學家G.M.Adelson-Velskii 和E.M.Landis在1962年

發明了一種解決上述問題的方法：當向二叉搜索樹中插入新結點后，如果能保證每個結點的左右子樹高度之差的絕對值不超過1(需要對樹中的結點進行調整)，即可降低樹的高度，從而減少平均搜索長度。

一棵AVL樹或者是空樹，或者是具有以下性質的二叉搜索樹：

它的左右子樹都是AVL樹
左右子樹高度之差(簡稱平衡因子)的絕對值不超過1(-1/0/1)

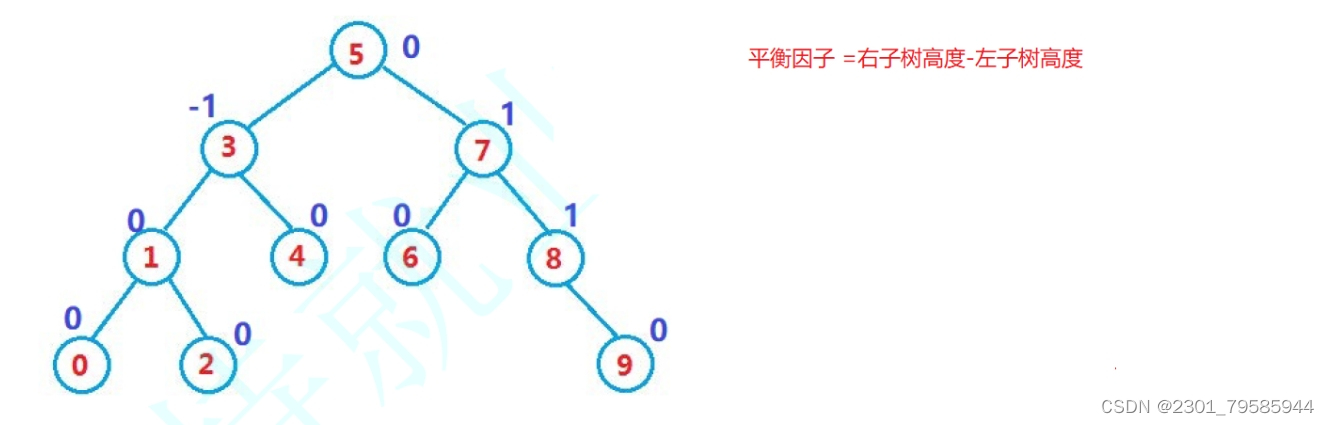
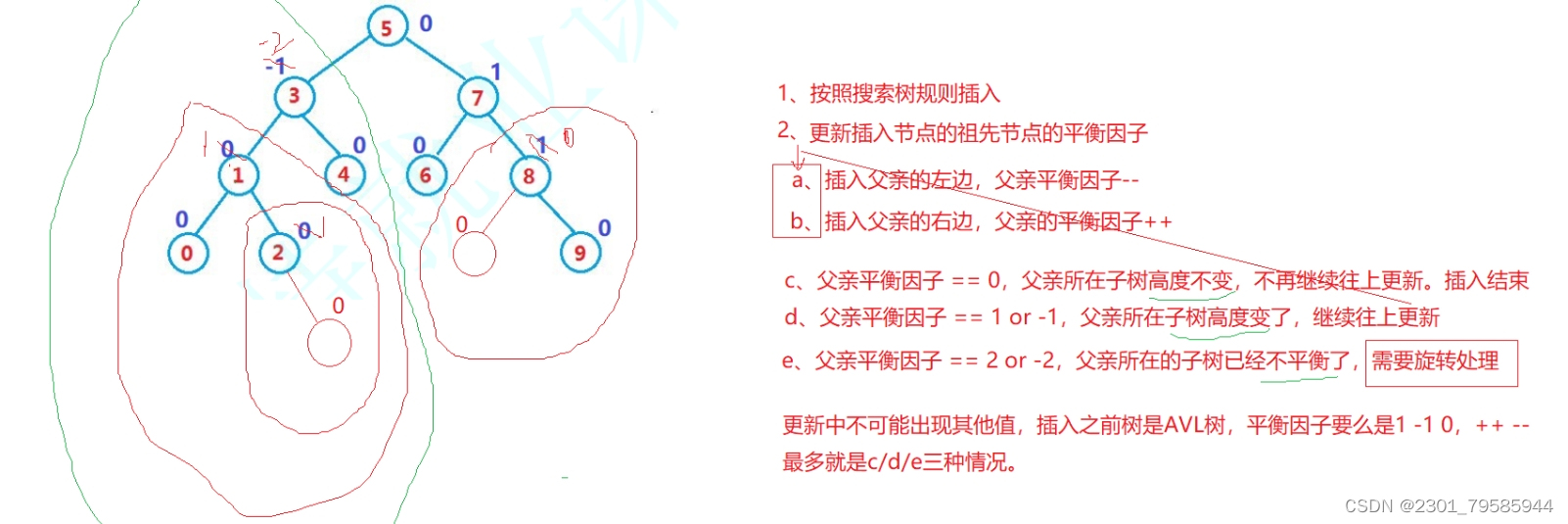
a、節點8的右子樹 - 左子樹，節點8的平衡因子為1；在8的左子樹新增一個節點，則8的平衡因子--，為0；
b、節點2的右子樹新增一個節點，2的右子樹 - 左子樹，則2的平衡因子++，為1；
d、2節點的平衡因子為1，則1節點右子樹所在高度變了，繼續往上更新，執行b操作，1節點平衡因子++，為1。

如果一棵二叉搜索樹是高度平衡的，它就是AVL樹。如果它有n個結點，其高度可保持在 $O(log_2 n)$，搜索時間復雜度O($log_2 n$)。

1.2、AVL樹節點的定義

template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;// 該節點的左孩子AVLTreeNode<K, V>* _right;// 該節點的右孩子AVLTreeNode<K, V>* _parent;// 該節點的父親節點pair<K, V> _kv;// pair類型的對象int _bf;  // balance factor平衡因子AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};

1.3、AVL樹的插入

AVL樹就是在二叉搜索樹的基礎上引入了平衡因子，因此AVL樹也可以看成是二叉搜索樹。那么 AVL樹的插入過程可以分為兩步：

按照二叉搜索樹的方式插入新節點
調整節點的平衡因子

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;// 二叉搜索樹不允許數據冗余while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 原先數據不存在，開始插入數據cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 保留新插入節點的父親節點//...// 更新平衡因子(右子樹 - 左子樹)while (parent){if (cur == parent->_left){// 插入的位置在左邊，則父親節點--；否則就++parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){// 更新結束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 繼續往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 當前子樹出問題了，需要旋轉平衡一下if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){}else if (parent->_bf == -2 && cur->_bf == 1){}break;// 旋轉完成之后：1、變平衡；2、高度不變，在往上的父親節點的平衡因子為0}else{// 理論而言不可能出現這個情況assert(false);}}return true;
}

1.4、AVL樹的旋轉

如果在一棵原本是平衡的AVL樹中插入一個新節點，可能造成不平衡，此時必須調整樹的結構，使之平衡化。根據節點插入位置的不同，AVL樹的旋轉分為四種：

1.4.1、新節點插入較高左子樹的左側---左左：右單旋

/*
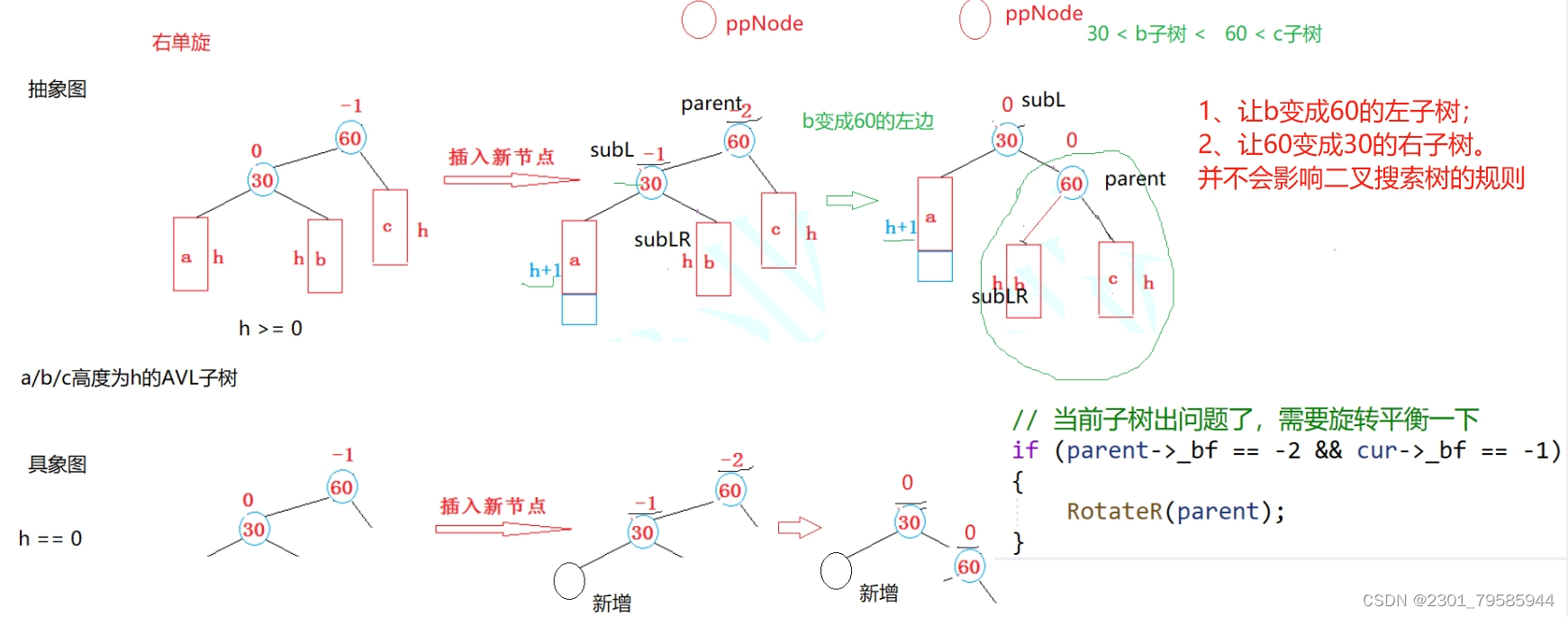
上圖在插入前，AVL樹是平衡的，新節點插入到30的左子樹(注意：此處不是左孩子)中，30左
子樹增加了一層，導致以60為根的二叉樹不平衡，要讓60平衡，只能將60左子樹的高度減少一層，右子
樹增加一層，即將左子樹往上提，這樣60轉下來，因為60比30大，只能將其放在30的右子樹，而如果30有
右子樹，右子樹根的值一定大于30，小于60，只能將其放在60的左子樹，旋轉完成后，更新節點的平衡因子即可。在旋轉過程中，有以下幾種情況需要考慮：
1. 30節點的右孩子可能存在，也可能不存在
2. 60可能是根節點，也可能是子樹
如果是根節點，旋轉完成后，要更新根節點
如果是子樹，可能是某個節點的左子樹，也可能是右子樹*/// 右單旋 ---> 從下往上更新到parent的平衡因子為-2的時候，需要發生旋轉(傳的是平衡因子為-2的父親節點)
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;// subL節點的右子樹不為空的話，才能更改subLR的父親節點if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppNode = parent->_parent;// parent節點不是根的話，提前保留parent節點的父親節點parent->_parent = subL;// parent為根if (parent == _root){_root = subL;// 根更新_root->_parent = nullptr;}// parent不為根else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}parent->_bf = subL->_bf = 0;
}

1.4.2、新節點插入較高右子樹的右側---右右：左單旋

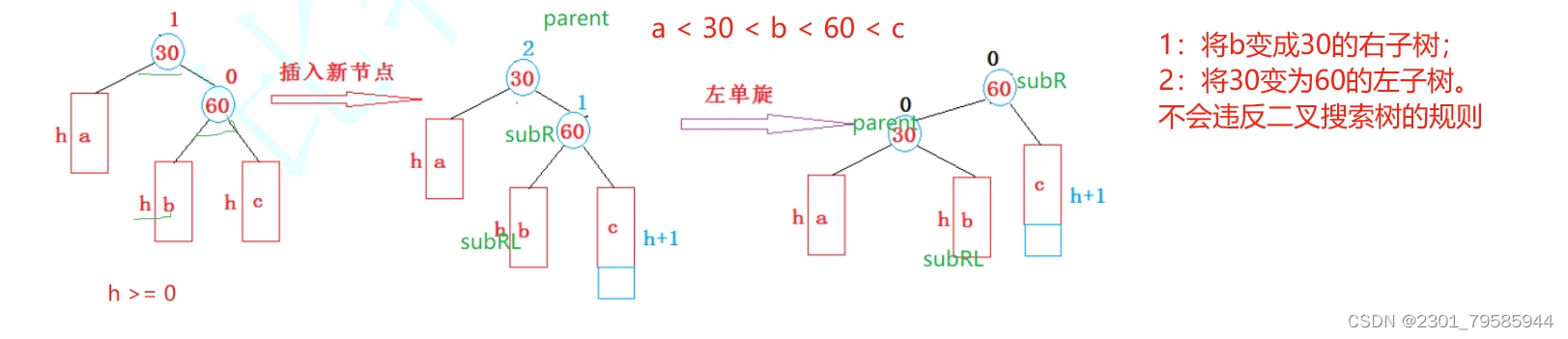
// 左單旋 ---> 從下往上更新到parent的平衡因子為2的時候，需要發生旋轉(傳的是平衡因子為2的父親節點)
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;// subRL節點不為空的話，才能更改subRL的父親節點if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppNode = parent->_parent;// parent節點不是根的話，提前保留parent節點的父親節點parent->_parent = subR;// parent為根if (parent == _root){_root = subR;_root->_parent = nullptr;}// parent不為根else{if (ppNode->_right == parent){ppNode->_right = subR;}else{ppNode->_left = subR;}subR->_parent = ppNode;}parent->_bf = subR->_bf = 0;
}

1.4.3、新節點插入較高左子樹的右側---左右：先左單旋再右單旋

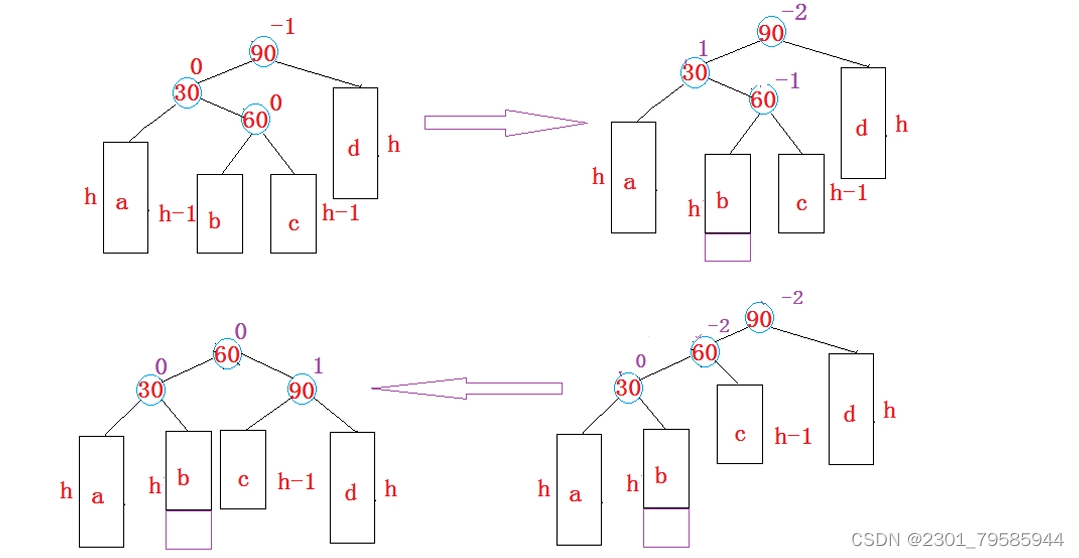
三種情況會引發旋轉：

如果h > 0，b插入，c的高度變為h，引發旋轉；
如果h > 0，c插入，c的高度變為h，引發旋轉；
如果h == 0，60為新增引發旋轉。

將雙旋變成單旋后再旋轉，即：先對30進行左單旋，然后再對90進行右單旋，旋轉完成后再考慮平衡因子的更新。

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == -1) // 情況一{subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 1) // 情況二{subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == 0) // 情況三{subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}

1.4.4、新節點插入較高右子樹的左側---右左：先右單旋再左單旋

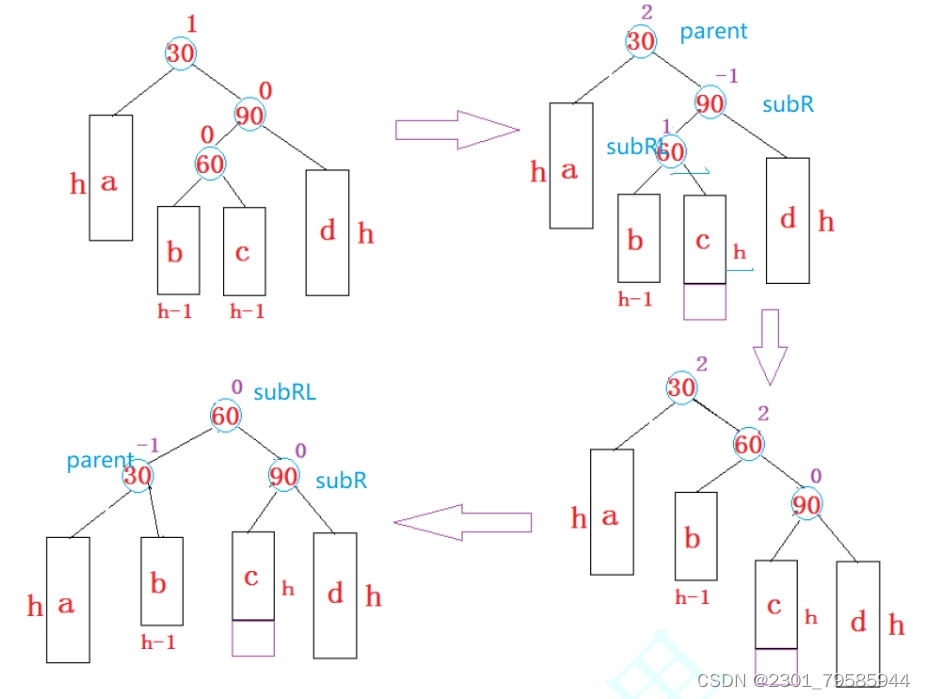
三種情況會引發旋轉：

如果h > 0，b插入，c的高度變為h，引發旋轉；
如果h > 0，c插入，c的高度變為h，引發旋轉；
如果h == 0，60為新增引發旋轉。

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);subRL->_bf = 0;if (bf == 1){// 在c位置插入subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){// 在b位置插入parent->_bf = 0;subR->_bf = 1;}else{// 60為新增parent->_bf = 0;subR->_bf = 0;}
}

總結：

假如以Parent為根的子樹不平衡，即Parent的平衡因子為2或者-2，分以下情況考慮

1. Parent的平衡因子為2，說明Parent的右子樹高，設Parent的右子樹的根為SubR

當SubR的平衡因子為1時，執行左單旋
當SubR的平衡因子為-1時，執行右左雙旋

2. Parent的平衡因子為-2，說明Parent的左子樹高，設Parent的左子樹的根為SubL

當SubL的平衡因子為-1是，執行右單旋
當SubL的平衡因子為1時，執行左右雙旋

旋轉完成后，原Parent為根的子樹個高度降低，已經平衡，不需要再向上更新。

1.5、AVL樹的驗證

AVL樹是在二叉搜索樹的基礎上加入了平衡性的限制，因此要驗證AVL樹，可以分兩步：

1. 驗證其為二叉搜索樹

如果中序遍歷可得到一個有序的序列，就說明為二叉搜索樹

	void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << endl;_InOrder(root->_right);}void InOrder(){// 一般在類里面寫遞歸都要套一層_InOrder(_root);}

void TestAVLTree1()
{int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();
}

2. 驗證其為平衡樹

每個節點子樹高度差的絕對值不超過1(注意節點中如果沒有平衡因子)
節點的平衡因子是否計算正確

bool _IsBalance(Node* root, int& height)
{if (root == nullptr){height = 0;return true;}int leftHeight = 0, rightHeight = 0;// 遞歸式的檢查每一個節點的左右子樹高度差與平衡因子是否相等// 改成后序，效率提高了if (!_IsBalance(root->_left, leftHeight)|| !_IsBalance(root->_right, rightHeight)){return false;}if (abs(rightHeight - leftHeight) >= 2){cout << root->_kv.first << "不平衡" << endl;return false;}// 左右子樹的高度差與平衡因子不相等if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子異常" << endl;return false;}// 保存該節點的高度height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;return true;
}bool IsBalance()
{int height = 0;return _IsBalance(_root, height);
}

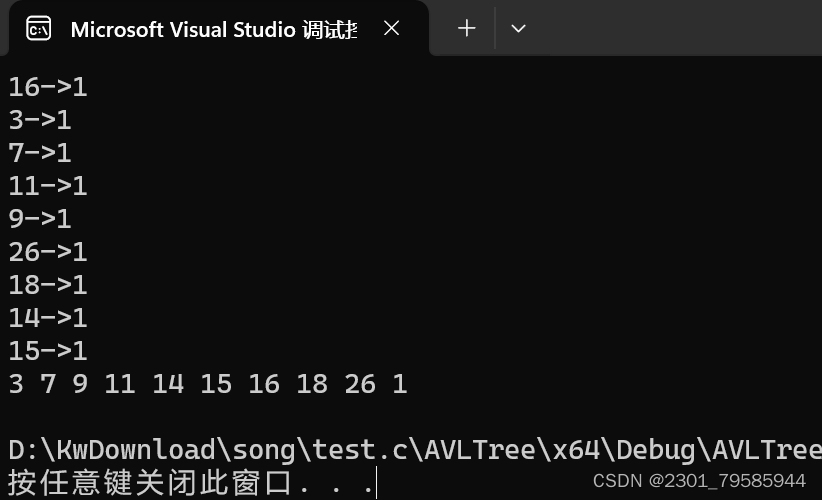
void TestAVLTree1()
{int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int, int> t;for (auto e : a){// 這是一個很好的調試技巧// 在if條件語句里打斷點來進行調試(空語句是打不住斷點的)if (e == 14){int x = 0;}t.Insert(make_pair(e, e));// 1、先看是插入誰導致出現的問題// 2、打條件斷點，畫出插入前的樹// 3、單步跟蹤，對比圖一一分析細節原因cout << e << "->" << t.IsBalance() << endl;}t.InOrder();cout << t.IsBalance() << endl;
}