制作不易，三連支持一下唄！！！

---

前言

這篇博客我們將來了解普通二叉樹的實現和應用，對大家之前分治和遞歸的理解有所挑戰。

---

一、二叉樹鏈式結構的實現

1.前置說明

在學習二叉樹的基本操作前，需要先創建一棵二叉樹，然后才能學習其相關的基本操作，由于我們現在對二叉樹結構的掌握還不夠深入，此處手動快速創建一棵二叉樹，等二叉樹結構了解差不多時，再研究二叉樹真正的創建方法。

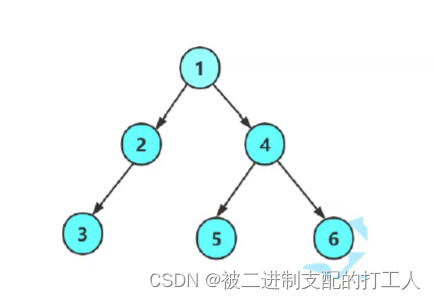
我們已這棵樹的結構為例，手動創建一顆二叉樹。?

typedef int BTDataType;typedef struct BinTreeNode
{struct BinTreeNode* left;struct BinTreeNode* right;BTDataType val;
}BTNode;BTNode* BuyBTNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("buynode:");return;}newnode->left = newnode->right = NULL;newnode->val = x;return newnode;
}BTNode* CreatTree()
{BTNode* n1 = BuyBTNode(1);BTNode* n2 = BuyBTNode(2);BTNode* n3 = BuyBTNode(3);BTNode* n4 = BuyBTNode(4);BTNode* n5 = BuyBTNode(5);BTNode* n6 = BuyBTNode(6);n1->left = n2;n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;return n1;
}

2.二叉樹的遍歷

①前序遍歷

根左右。前序遍歷首先訪問根結點然后遍歷左子樹，最后遍歷右子樹。在遍歷左、右子樹時，仍然先訪問根節點，然后遍歷左子樹，最后遍歷右子樹。
若二叉樹為空則結束返回，否則：
（1）訪問根結點。
（2）前序遍歷左子樹。
（3）前序遍歷右子樹 。
需要注意的是：遍歷左右子樹時仍然采用前序遍歷方法。

根據前序遍歷的概念可以看出，前序遍歷是遞歸展開的。我們代碼實現時就應該按照分治的思想來書寫。

//前序遍歷
void PreOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);}

在用分治思想解決問題時，我們要抓住這兩個重點：

1.想清楚子問題是什么

2..想清楚什么時候是最小子問題。

例如上面二叉樹的前序遍歷，子問題就是要想遍歷這棵樹要將它分為根，左子樹，右子樹。

左子樹又分為根，左子樹，右子樹……依次類推。最小子問題就是當這棵樹為空樹也就是NULL時，我們逐層返回。

②中序遍歷

左根右。中序遍歷首先遍歷左子樹，然后訪問根結點，最后遍歷右子樹。

與前序遍歷類似，代碼實現如下：

//中序遍歷
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PreOrder(root->left);printf("%d ", root->val);PreOrder(root->right);
}

③后序遍歷

左右根。后序遍歷首先遍歷左子樹，然后遍歷右子樹，最后訪問根結點，在遍歷左、右子樹時，仍然先遍歷左子樹，然后遍歷右子樹，最后遍歷根結點。即：
若二叉樹為空則結束返回，
否則：
（1）后序遍歷左子樹
（2）后序遍歷右子樹
（3）訪問根結點

//后序遍歷
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PreOrder(root->left);PreOrder(root->right);printf("%d ", root->val);
}

④層序遍歷?

層序遍歷就是一層一層按順序遍歷樹，方法就是借助隊列的性質，出隊列一個就帶兩個子節點就隊列的方法來遍歷，直到隊列為空，如果出隊列的節點為空就不帶節點進隊列了！！！

void TreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){printf("%d ", front->val);// 帶入下一層QueuePush(&q, front->left);QueuePush(&q, front->right);}else{printf("N ");}}printf("\n");QueueDestroy(&q);
}

3.求二叉樹的節點數?

這里我們要寫一個求給定二叉樹有多少節點的接口

我們還是采用分治的思想，要求一顆二叉樹有多少節點還是將它分為左子樹和右子樹，先求出左右子樹有多少節點，最后再加上根節點這一個就可以了。最小子問題還是遇到空樹就返回0個節點。

int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

4.求二叉樹的深度?

我們還是采用分治的思想，要求一顆二叉樹的深度還是將它分為左子樹和右子樹，先求出左右子樹的深度中的最大值，再加上根節點的1。最小子問題還是遇到空樹就返回0。

int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}int leftdepth = TreeHeight(root->left);int rightdepth = TreeHeight(root->right);return (leftdepth > rightdepth ? leftdepth : rightdepth) + 1;
}

這里有一個注意點：

可能有些同學會試圖將代碼簡化，不創建leftdepth和rightdepth兩個變量，直接返回。

?

單從結果上來看，這樣寫是沒有什么問題的。問題出在這樣寫會使時間復雜度暴增。

之前時間復雜度是O（N），但現在時間復雜度甚至接近2^N。

在leetcode上有一道求二叉樹深度題目，如果用改動之后的代碼提交上無法通過的，因為效率太低了。

. - 力扣（LeetCode）

5.求第K層節點個數

分治思想：要求第K層節點個數可將問題拆分為求左子樹的第K-1層的節點個數和右子樹的第K-1層節點個數之后，依此類推。

最小子問題①非空且K==1時就返回1，

②如果根已經為空就返回0。

int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (NULL == root)return 0;if (k == 1)return 1;//如果不為空且k不等于1，就說明第k層在子樹中，轉換為子問題求解return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

6.查找值為x的節點的位置?

分治思想：子問題是在左子樹找和在右子樹找

最小子問題是：如果根為空就返回空，如果根不為空且val==x就返回root

BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL)return NULL;if (root->val == x)return root;BTNode* ret1 = TreeFind(root->left, x);if (ret1)return ret1;return  TreeFind(root->right, x);
}

7. 二叉樹的創建和銷毀

1.創建

二叉樹的創建要依靠前序遍歷的結果或中序遍歷的結果或后序遍歷的結果來構建，后面我們有相關題目，這里不多贅述。

2.銷毀

void TreeDestroy(BTNode* root)
{if (root == NULL)return;TreeDestroy(root->left);TreeDestroy(root->right);free(root);root = NULL;
}

---

總結

我們詳細了解了二叉樹的存儲結構，并初步領會了分治思想