操作環境：

MATLAB 2022a

1、算法描述

差分進化算法（Differential Evolution, DE）是一種有效的實數編碼的進化算法，主要用于解決實值函數的全局優化問題。本文將詳細介紹差分進化算法的背景、原理、操作步驟、參數選擇以及實際應用，旨在提供一個全面的理解。

1. 差分進化算法的背景

差分進化算法由Storn和Price在1997年提出，最初是為了解決Chebyshev多項式的優化問題。由于其簡單、高效、易于實現等特點，DE迅速成為解決各種復雜優化問題的熱門選擇，尤其在工程優化、經濟學、生物信息學等領域得到廣泛應用。

2. 差分進化算法的原理

差分進化算法基于種群的迭代搜索。其基本思想是通過種群中個體間的差分信息引導搜索過程，通過迭代更新種群，逐漸逼近全局最優解。DE算法主要包含四個基本操作：初始化、變異、交叉和選擇。

2.1 初始化

差分進化算法首先隨機生成一個包含NP個D維實數向量的初始種群。每個向量代表一個潛在的解。初始種群通常在問題定義的邊界內隨機生成。

2.2 變異

對于種群中的每一個目標向量 𝑥𝑖,𝑔xi,g?，算法通過以下公式生成一個變異向量 𝑣𝑖,𝑔+1vi,g+1?：

𝑣𝑖,𝑔+1=𝑥𝑟1,𝑔+𝐹×(𝑥𝑟2,𝑔?𝑥𝑟3,𝑔)vi,g+1?=xr1,g?+F×(xr2,g??xr3,g?)

其中，𝑟1,𝑟2,𝑟3r1,r2,r3 是從種群中隨機選擇的三個不同的索引，𝐹F 是縮放因子，用于控制差分擾動的幅度。

2.3 交叉

交叉操作用于增加種群的多樣性。對于每個目標向量和對應的變異向量，算法按照一定的交叉概率CR進行交叉操作，生成試驗向量 𝑢𝑖,𝑔+1ui,g+1?：

{𝑣𝑗,𝑖,𝑔+1if?𝑟𝑎𝑛𝑑𝑗(0,1)≤𝐶𝑅?or?𝑗=𝑟𝑎𝑛𝑑(𝑖)𝑥𝑗,𝑖,𝑔otherwise{vj,i,g+1?xj,i,g??if?randj?(0,1)≤CR?or?j=rand(i)otherwise?

其中，𝑟𝑎𝑛𝑑𝑗(0,1)randj?(0,1) 是一個隨機數，𝑟𝑎𝑛𝑑(𝑖)rand(i) 是一個隨機選擇的維度索引，保證每個試驗向量至少有一個來自變異向量的分量。

2.4 選擇

選擇操作基于貪心策略。對于每個目標向量和對應的試驗向量，如果試驗向量的適應度（通常是目標函數值）優于目標向量的適應度，那么在下一代種群中替換目標向量；否則，目標向量保持不變。

3. 參數選擇

差分進化算法的性能在很大程度上依賴于參數的選擇，主要包括種群大小NP、縮放因子F和交叉概率CR。種群大小NP影響算法的多樣性和收斂速度；縮放因子F影響搜索步長，過大可能導致過快收斂，過小可能導致收斂速度慢；交叉概率CR決定了試驗向量的多樣性。

4. 實際應用

差分進化算法由于其結構簡單和高效性，在許多實際應用中都表現出色。例如，在工程設計中優化結構尺寸，在生物信息學中用于基因表達數據的特征選擇，在金融領域優化投資組合等。

2、仿真結果演示

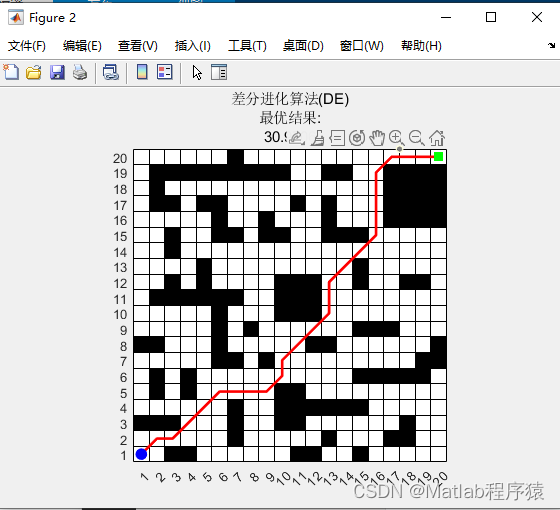
3、關鍵代碼展示

略

4、MATLAB?源碼獲取

? ? ? V

點擊下方名片