【碎碎念】最近的任務有點繁重,所以考慮到實際情況,視頻學習決定放置一段時間,重點是學校的實訓練習題,對于我而言,目標不是優秀/良好,綜合考慮我的實際情況,保佑我及格、順利通過就可!加油!
今日學習任務
1.復習代碼
2.習題(Cleaning Shifts、Vanya and Lanterns)
復習代碼
Anton and Letters(搞定)
#include<stdio.h>
int main(){int flag[26];for(int i=0;i<=26;i++) flag[i]=0;char tmp;while(tmp!='}'){scanf("%c",&tmp);if(tmp=='}') break;if(tmp<'z'&&tmp>='a'){flag[tmp-'a']++;//需要記憶 }}int cnt=0;//需要記得初始化 for(int i=0;i<26;i++){if(flag[i]>0) cnt++;}printf("%d",cnt);
}Sum of Digits(搞定)
#include<stdio.h>
#include<stdlib.h>
#include<string.h>char s[10000];
int sum=0;
int result =0;int main(){scanf("%s",s);while(1){if(strlen(s)==1) break;for(int i=0;i<strlen(s);i++){sum+=s[i]-'0';}itoa(sum,s,10);result++;}printf("%d",result);return 0;
}寒冰王座(搞定)
#include<stdio.h>
int main(){int T,i,n,sum;while(scanf("%d",&T)!=EOF){if(T<1||T>100) break;for(i=0;i<T;i++){scanf("%d",&n);if(n<1||n>10000) break;if(n>=300) sum=n%50;else if (n>=150&&n<200) sum=n-150;else if (n>=200&&n<300) sum=n-200;else if (n<150) sum=n;printf("%d\n",sum);}//if(n<1||n>10000) break;}return 0;
}Charm Bracelet(搞定)
#include <stdio.h>
int main(){//第一行輸入 兩個空格分隔的整數int n,m;scanf("%d %d",&n,&m) ;//定義狀態int dp[12881] ;//初始化dp[i]=0 for(int i=0;i<=m;i++){dp[i]=0;}//轉移方程for(int i=1;i<=n;i++) {//注意 i=1 //定義重量和價值 兩個空格分隔的整數描述魅力i: W i和D iint w,d;scanf("%d %d",&w,&d) ;for(int j=m;j>=w;j--){//注意j>=wif(dp[j-w]+d>dp[j])dp[j]=dp[j-w]+d;}}printf("%d\n",dp[m]);return 0;
}習題
Cleaning Shifts
如果考試遇到這道題,可以先跳過
思路已掌握
問題
描述:
農夫大衛有一片菜園,同時他有n條狗(1 ≤ n ≤ 25000)來看守。他的每條狗有固定的工作時間,并且一定能在工作時間內好好看守菜園。他把一天的時間分為t個時間段(1 ≤ t ≤ 1000000),分別是從1到t,希望每個時間段都至少有一條狗看守菜園。請你為這些狗分配工作,計算最少需要幾條不同的狗,才能讓每個時間段都至少有一條狗有看守菜園。注意,有可能不論怎么安排,都無法實現這個目標。輸入:
第一行輸入是以空格分隔的兩個整數n和t。第2行到第n+1行包含每條狗的工作時間,以兩個空格分隔的整數表示,代表著這條狗工作的第一個時間段和最后一個時間段。輸出:
完成農夫大衛的目標需要的最少的狗的數量。如果不能完成該目標,輸出-1。樣例1:
輸入: 3 10 1 7 3 6 6 10輸出: 2樣例2:
輸入: 4 100 21 50 50 81 1 20 80 99輸出: -1
思路
【挑戰程序設計競賽 2章習題 poj 2376 Cleaning Shifts】 https://www.bilibili.com/video/BV13K421h7n5/?share_source=copy_web&vd_source=c1510692b9cb6018bf78570791d3ee02
代碼思路
-
定義結構體與輸入:首先定義了一個結構體
node來存儲區間信息,包含起始時間a和結束時間b。通過scanf接收輸入的區間數量n和總時間t,隨后逐個讀取每個區間的起始和結束時間。 -
自定義排序:使用
cmp函數作為比較器,實現了按區間起始時間升序排列,若起始時間相同則按結束時間降序排列,確保優先選擇結束時間更晚的區間進行覆蓋。通過sort函數對區間進行排序。 -
區間覆蓋判斷與計數:
- 首先檢查第一個區間的起始時間是否為1,如果不是,則直接輸出-1,表示無法覆蓋整個區間。
- 初始化
end為第一個區間的結束時間,sum也為end,并設置已使用的區間計數cnt為1。 - 遍歷排序后的區間列表,對于每個區間,如果它的起始時間在當前已選區間結束時間的下一個位置或之內(即
a[i].a<=end+1),則嘗試更新最遠的覆蓋點為兩者中的最大值(通過max(sum, a[i].b))。 - 如果當前區間的起始時間大于
end+1,說明當前區間無法接續前一區間,此時需要判斷是否可以形成新的覆蓋段:如果新區間的起始時間仍然在當前覆蓋段的結束時間之后(即a[i].a>end+1),則直接輸出-1;否則,增加計數器cnt,并將end更新為上一覆蓋段的最遠端點,然后繼續嘗試將當前區間加入覆蓋。 - 最后,檢查最終覆蓋的最遠端點
end是否等于總時間t,如果不等則輸出-1,表示未完全覆蓋;否則輸出cnt作為最少所需區間的數量。
記憶方法
-
理解核心邏輯:關鍵是理解區間覆蓋的貪心策略,即優先選擇結束時間更晚的區間來嘗試覆蓋更長的連續時間線。
-
掌握排序技巧:記住如何根據問題需求自定義排序規則,這里是為了在遍歷時優先考慮起始時間早且結束時間晚的區間。
-
區間迭代的分支處理:熟悉如何在遍歷過程中分情況討論區間能否連續覆蓋,特別是如何通過更新
end和sum變量來維護當前的覆蓋狀態。 -
邊界條件檢查:特別注意代碼中對邊界條件的檢查,比如起始時間不為1的情況,以及最終覆蓋是否完整,這些是決定輸出結果的關鍵。
代碼
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <algorithm>
#include <stdio.h>using namespace std;const int N = 1000010;/*
Sample Input3 10
1 7
3 6
6 10
Sample Output2
*/
int n;
struct Range
{int l, r;bool operator< (const Range& W)const{return l < W.l;}
}range[N];int main()
{int st, ed;scanf("%d%d", &n, &ed);st = 1;for (int i = 0; i < n; i++){int l, r;scanf("%d%d", &l, &r);range[i].l = l; range[i].r = r;}sort(range, range + n);int res = 0;bool success = false;for (int i = 0; i < n; i++){int j = i, r = -2e9;//所有區間起點在當前點前的 取終點最遠的那個區間while (j < n && range[j].l <= st){r = max(r, range[j].r);j++;}//如果所有區間都在當前點之前 那就無法覆蓋了 返回-1 跳出if (r < st){res = -1;break;}//選擇區間個數加1res++;//選擇后的所有區間已經覆蓋到終點或者終點之后 那就得到了答案了if (r >= ed){success = true;break;}//更新當前點 繼續下一輪尋找可覆蓋的區間st = r + 1;i = j - 1;}if (!success) res = -1;printf("%d\n", res);return 0;
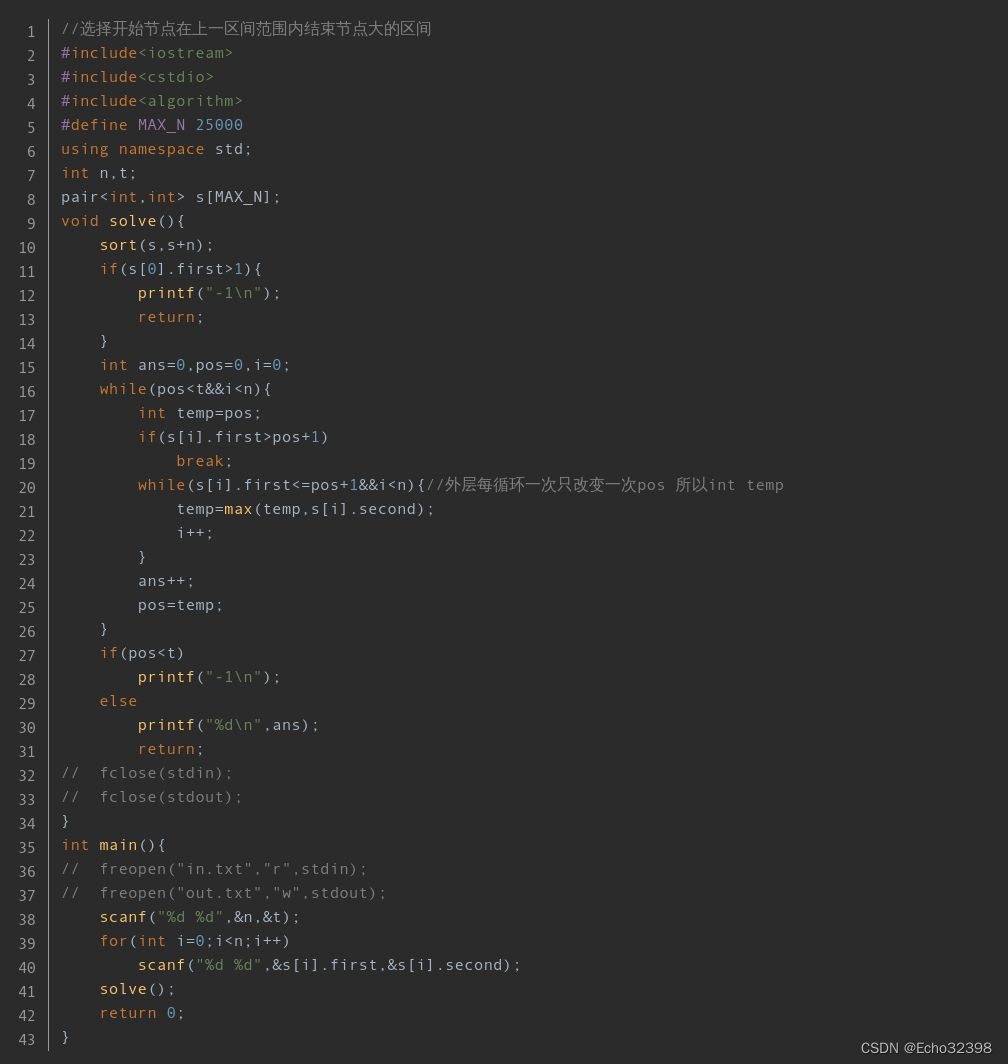
}
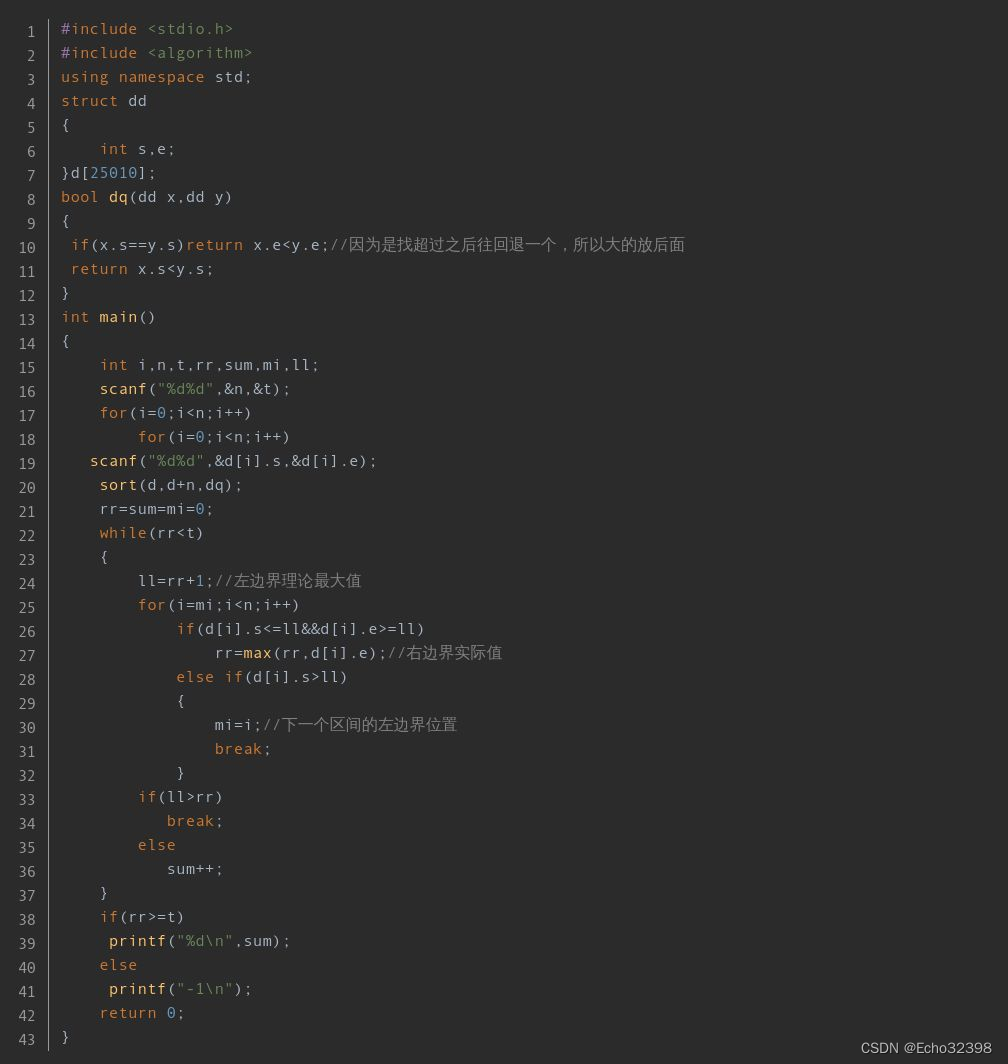
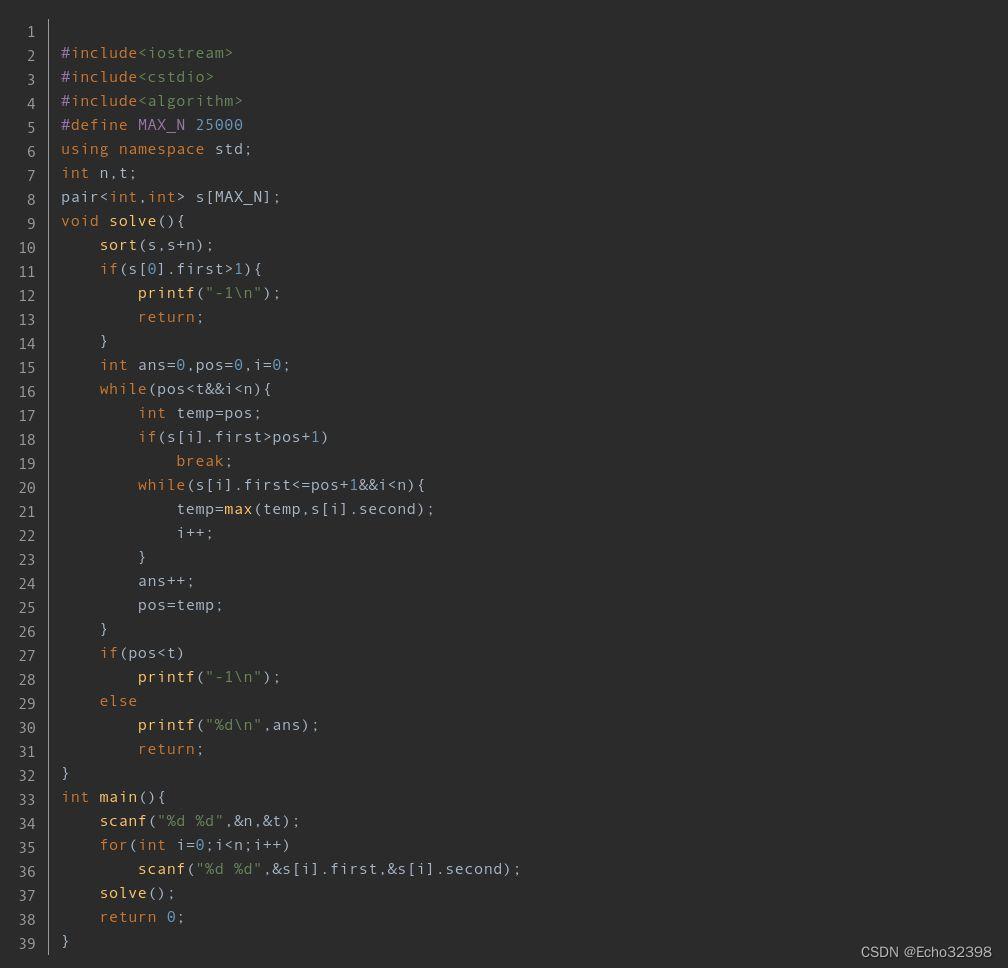
#include <iostream>
#include<algorithm>
#include <stdio.h>
using namespace std;
struct node
{int a,b;
};
struct node a[2500005];
bool cmp(node a,node b)
{if(a.a==b.a) return a.b>b.b;else return a.a<b.a;
}
//結構體排序的比較函數
int main()
{int t,n;scanf("%d%d",&n,&t);for(int i=1; i<=n; i++){scanf("%d%d",&a[i].a,&a[i].b);}
//習慣從1開始寫sort(a+1,a+1+n,cmp);
//排序if(a[1].a!=1){printf("-1\n");return 0;}
//如果開頭值都做不到等于1,那不管后面如何肯定覆蓋不了所有區間int end=a[1].b,sum=end,cnt=1;
//因為先確定了end,所以cnt的值為1for(int i=2; i<=n; i++){if(a[i].a<=end+1){sum=max(sum,a[i].b);}
//若每次比較的左斷點在上一段區間的里面或等于end+1即end的旁邊,就不斷進行比較滿足條件中最遠的點,即sum最大。else{end=sum;if(a[i].a>end+1){printf("-1\n");return 0;}else{cnt++;if(a[i].a<=end+1){sum=max(sum,a[i].b);}}}}if(end!=sum){cnt++;end=max(sum,end);}if(end!=t) printf("-1\n");else printf("%d\n",cnt);return 0;
}Vanya and Lanterns
問題
一條長為?L?的路,在坐標軸上范圍是?[0,L],在?n個位置都放置了路燈,燈光能覆蓋的半徑相同,問半徑至少為多少時燈光可以覆蓋整條路。
Input
第一行包含兩個整數?n,l(1≤n≤1000,1≤L≤109)分別代表路燈的數量和這條路的長度。
第二行包含?n個整數?ai(0≤ai≤L),即各個路燈所在的位置。
注意:多個路燈可能在同一位置,而且可能有路燈位于這條路的端點。Output
輸出一個精確到小數點后?99?位的實數?r,代表能使燈光可以覆蓋整條路的情況下,路燈燈光半徑的最小值。
思路
解題說明:題目的意思是有一條長度為 l 的街道,在這條街道上放置了n個相同的燈,設從一端位置為0,每個燈的位置在ai處,問燈的最小照射半徑為多少時,才能滿足整條街道都能被燈光照到。此題可以用貪心來做,由于除了兩端的兩個燈之外,每兩個燈之間都是由兩個燈共同照射的,故只需要求出兩兩燈之間的距離一半的最大值,再求出兩端兩個燈距離街道兩端盡頭的距離,三者的最大值就是所求的最小半徑。
代碼
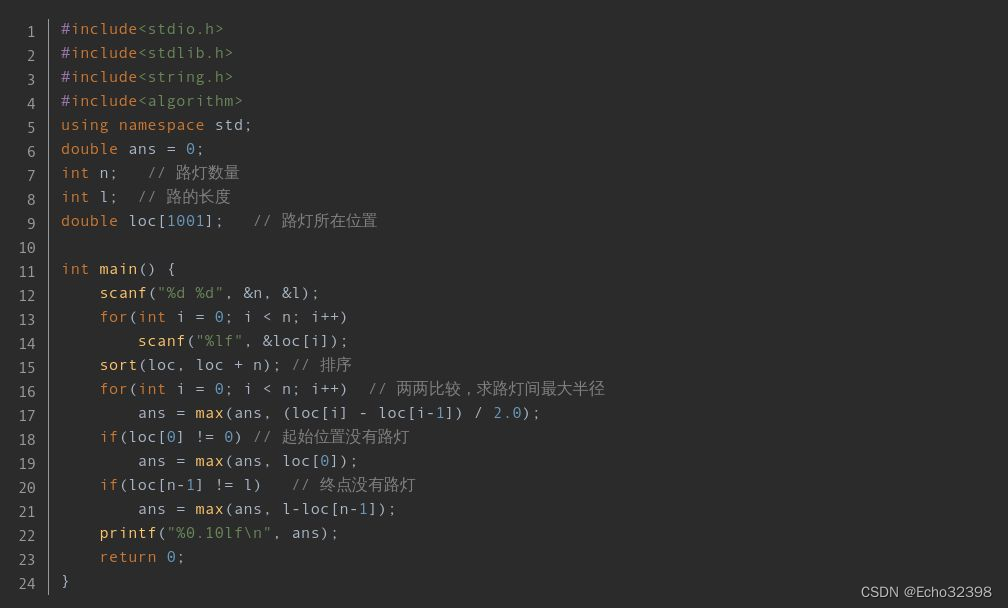
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<algorithm>
using namespace std;double ans=0;//半徑
int n;//路燈數量
int l;//路的長度
double loc[1001];//路燈所在位置 int main(){scanf("%d %d",&n,&l);for(int i=0;i<n;i++)//路燈的位置 scanf("%lf",&loc[i]);sort(loc,loc+n) ;for(int i=0;i<n;i++)//兩兩比較,求路燈最大值 ans=max(ans,(loc[i]-loc[i-1])/2.0) ;if(loc[0]!=0)//起始無路燈ans=max(ans,loc[0]) ;if(loc[n-1]!=l)//終點無路燈ans=max(ans,l-loc[n-1]) ;printf("%.010lf\n",ans);return 0;
}


)




函數和stoll函數)
-百變屏幕無壓力,這才是Android屏幕適配的終極解決方案)
----單級放大器(共源極))








