目錄
背景知識
什么是神經網絡?
神經網絡發展史
MP神經元模型
感知機模型
KAN
引言
MLP架構vsKAN架構
從數學定理方面來看:
從算法層面上看:
從實際應用過程看:
KAN的架構細節
KAN的準確性
KAN的可解釋性
監督學習
無監督學習
數學領域
物理領域
自動和手動模式的比較
何時該選用 KAN?
背景知識
什么是神經網絡?
神經網絡是一種模仿生物神經網絡結構和功能的非線性數學模型

神經網絡發展史

MP神經元模型
當前神經元會收到x1到xn傳來的信號,這些輸入信號會通過w1到wn的權重,與當前神經元進行連接,從而傳遞信息。

感知機模型

KAN
引言
弗拉基米爾·阿諾德和安德烈·科爾莫戈羅夫證明了,如果f是有界域上的多變量連續函數,則f可以寫成單變量連續函數和加法二元運算的有限組合。
即“任何一個多變量連續函數都可以表示為一些單變量函數的組合”

KAN 的名字也由此而來。
正是受到這一定理的啟發,研究人員用神經網絡將 Kolmogorov-Arnold 表示參數化。
為了紀念兩位偉大的已故數學家 Andrey Kolmogorov 和 Vladimir Arnold,我們稱其為科爾莫格羅夫-阿諾德網絡(KANs)。
MLP架構vsKAN架構
? ? ? ? ?跟 MLP 最大、也是最為直觀的不同就是,MLP 激活函數是在神經元上,而 KAN 把可學習的激活函數放在權重上。
從數學定理方面來看:
? ? ? ? MLP 的靈感來自于通用近似定理,即對于任意一個連續函數,都可以用一個足夠深的神經網絡來近似。
而 KAN 則是來自于 Kolmogorov-Arnold 表示定理 (KART),每個多元連續函數都可以表示為單變量連續函數的兩層嵌套疊加。
從算法層面上看:
? ? ? ? MLPs 在神經元上具有(通常是固定的)激活函數
? ? ? ? 而 KANs 在權重上具有(可學習的)激活函數。這些一維激活函數被參數化為樣條曲線。
從實際應用過程看:
? ? ? ? KAN 可以直觀地可視化,提供 MLP 無法提供的可解釋性和交互性。

KAN的架構細節

左側的圖顯示了 KAN 的分層架構。每層包括一組節點,每個節點都通過一組特定的函數處理輸入數據,輸出到下一層。每個節點上的小圖標表示的是激活函數的形式,這里用B-樣條函數作為激活函數。
右側的圖展示了一個激活函數 ?(x),它被參數化為一個B-樣條函數。圖中還展示了如何通過改變B-樣條的節點(也稱為控制點)數量來調整函數的粒度。
這張圖的核心在于展示KAN如何通過使用B-樣條作為激活函數,結合網絡的多層結構和激活函數的動態調整(網格擴展技術),來處理復雜的高維數據。這種設計使得網絡不僅能適應不同的數據分辨率,還能通過調整激活函數的精度來優化性能。
KAN的準確性
神經縮放規律:KAN 的縮放速度比 MLP 快得多。除了數學上以 Kolmogorov-Arnold 表示定理為基礎,KAN 縮放指數也可以通過經驗來實現。

函數擬合:KAN 比 MLP 更準確。
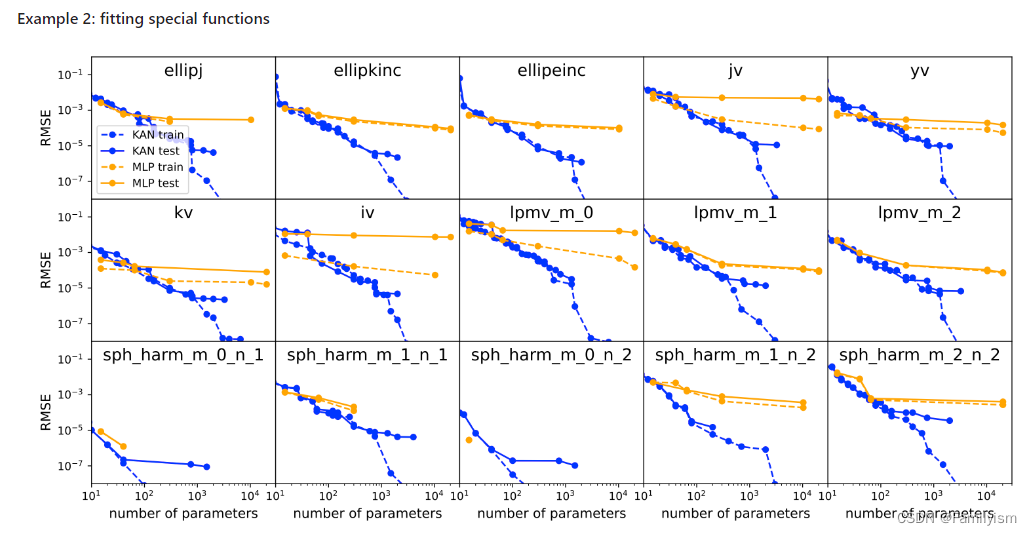
偏微分方程求解:比如求解泊松方程,KAN 比 MLP 更準確。
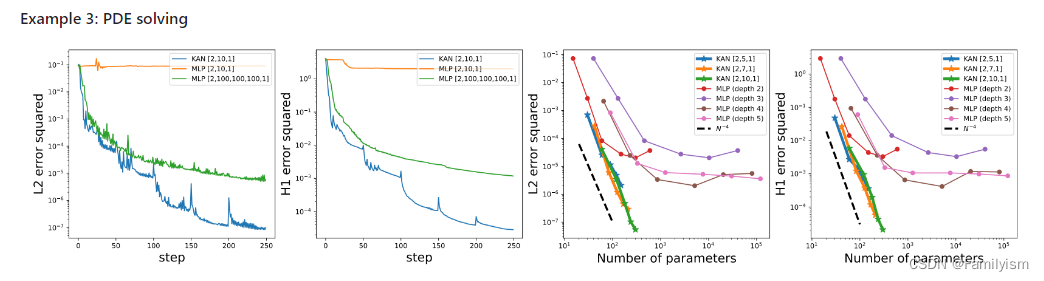
規避災難性遺忘:KAN 不會像 MLP 那樣容易災難性遺忘,它天然就可以規避這個缺陷。

KAN的可解釋性
監督學習
在可解釋方面,KAN 能通過符號公式揭示合成數據集的組成結構和變量依賴性。

無監督學習

在無監督學習中,目標是識別數據中變量之問的依賴關系,而不是預測輸出,KANS通過修改其結構,能夠識別哪些輸入變量是相互依賴的。左圖(seed=0)和右圖(seed =2024)顯示了相同的數據集但不同的初始化種子如何導致KAN 學到不同的依賴關系結構。 KAN 通過其靈活的網絡結構捉供了一種強大的工具來探索這些關系,從而增強了模型的解釋性和應用的廣泛性
數學領域

用KAN來解決結點理論問題: 圖a顯示使用 17 個變量的網絡結構實現了81.6%的測試準確率。僅使用3個最重要的變量精簡后的模型達到了78.2%的測試準確率。圖(c)通過餅圖展示了三個變量對預測結果的貢獻比例。
物理領域

本文用KAN來探索和解釋物理模型中的動力學邊界,尤其是在量子系統的安德森局域化現象中的應用
自動和手動模式的比較
人類用戶可以與 KANs 交互,使其更具可解釋性。在 KAN 中注入人類的歸納偏差或領域知識非常容易。

何時該選用 KAN?

關于這個問題,主要看想要的是什么?如果效率優先,也就是最右邊這條支路,選MLP,因為目前,KANS訓練速度較慢是其主要瓶頸,通常比 MLPS慢10倍。但如果想要小模型,KAN更好。如果可解釋性優先,選中間,那么KAN牛遍。如果準確性優先,最左邊,KAN 也更牛通,盡管 KAN 顯示了不錯的前景,但畢竟剛開始,還很不足。

)



技術)




)





)


)