摘要
知識蒸餾涉及使用基于共享溫度的softmax函數將軟標簽從教師轉移到學生。然而,教師和學生之間共享溫度的假設意味著他們的logits在logit范圍和方差方面必須精確匹配。這種副作用限制了學生的表現,考慮到他們之間的能力差異,以及教師天生的logit關系足以讓學生學習。為了解決這個問題,我們建議將溫度設置為logit的加權標準差,并在應用softmax和KL散度之前進行logit標準化的即插即用Z-score預處理。我們的預處理使學生可以關注教師的基本Logit關系,而不是要求大小匹配,并且可以提高現有基于logit的蒸餾方法的性能。我們還展示了一個典型的例子,其中教師和學生之間的傳統共享溫度設置不能可靠地產生真實的蒸餾評估;然而,我們的Z-score成功地緩解了這一挑戰。
介紹
Hinton等人首先提出通過最小化他們預測之間的KL散度,將教師的知識提煉給學生。這里softmax函數的縮放因子,稱為溫度T,它的引入是為了軟化預測概率。傳統上,溫度是預先全局設置的超參數,并在整個訓練過程中保持固定。CTKD采用對抗學習模塊來預測樣本溫度,以適應不同的樣本難度。然而,現有的基于logit的KD方法仍然假設教師和學生應該共享溫度,忽略了KL散度中不同溫度值的可能性。在這項工作中,我們證明了分類和KD中的一般softmax表達式是從信息論中的熵最大化原理推導出來的。在這個推導過程中,拉格朗日乘數出現,并以溫度的形式出現,在此基礎上,我們建立了教師和學生的溫度之間的不相關性,以及不同樣本的溫度之間的不相關性。這個證明支持我們在教師和學生之間以及在樣本之間分配不同溫度的動機。
對比logit預測的精確匹配,發現預測的類間關系足以使學生達到與教師相似的成績。一個輕量級的學生在預測具有可比范圍和方差的對數時面臨著與一個笨重的教師相比的挑戰。然而,我們證明在KL散度中共享溫度的傳統做法仍然隱含地強制學生和教師logit之間的精確匹配。現有的基于logit的KD方法沒有意識到這個問題,通常會陷入陷阱,導致整體性能下降。為了解決這個問題,我們建議**使用加權logit標準偏差作為自適應溫度,并在應用softmax之前將Z-score logit標準化作為預處理步驟。**這種預處理將logit的任意范圍映射到有界范圍,允許學生logit具有任意范圍和方差,同時有效地學習和保留教師logit的固有關系。我們提出了一個典型的案例,其中在softmax中共享溫度設置下的KL散度損失可能會產生誤導,并且不能可靠地衡量蒸餾學生的表現。相比之下,使用我們的Z-score預處理,在這種情況下消除了共享溫度的問題。
貢獻
(1)基于信息論中的熵最大化原理,利用拉格朗日乘子導出了基于logit的KD中softmax的一般表達式。我們表明,溫度來自于衍生的乘數,允許它被不同的樣本和不同的學生和老師選擇。
(2)為了解決由共享溫度引起的傳統基于logit的KD管道的問題,包括隱式強制logit匹配和學生模型不真實的索引。我們提出了一種logit蒸餾的預處理,以自適應地在教師和學生之間以及跨樣本分配溫度,能夠促進現有的基于logit的KD方法。
Background and Notation
我們擁有一個轉移數據集D包含所有N樣本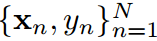 ,這里
,這里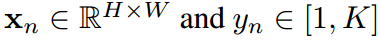 分別是第n個樣本的圖片和標簽。H,W,K是圖片的高度、寬度和類的數量。給定一個輸入
分別是第n個樣本的圖片和標簽。H,W,K是圖片的高度、寬度和類的數量。給定一個輸入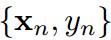 ,教師
,教師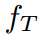 和學生
和學生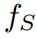 分別預測logit向量
分別預測logit向量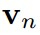 和
和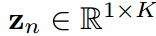 。即
。即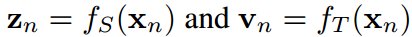 ,
,
人們普遍接受的是,使用涉及溫度T的softmax函數將logit轉換為概率向量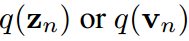 ,使它們的第k項具有:
,使它們的第k項具有:
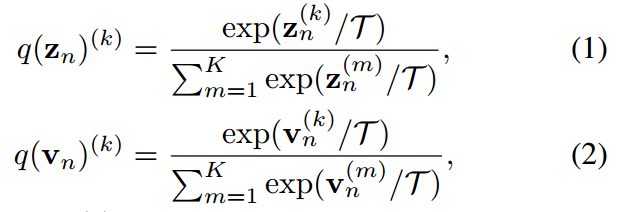
其中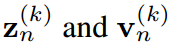 ,分別是
,分別是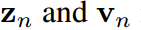 的第k項。知識蒸餾的過程本質上是讓
的第k項。知識蒸餾的過程本質上是讓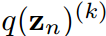 模擬
模擬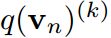 對任何類和所有樣本。目標是通過最小化KL散度來實現的。
對任何類和所有樣本。目標是通過最小化KL散度來實現的。
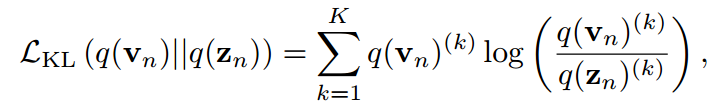
當只對z進行優化時,理論上等于交叉熵損失:
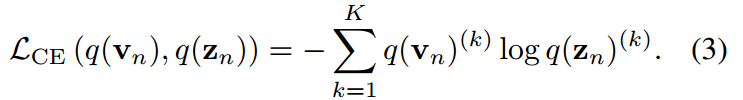
注意,它們在經驗上是不等價的,因為它們的梯度由于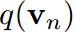 的負熵項而發散。
的負熵項而發散。
方法
溫度之間的不相關性
在第4.1.1和4.1.2中,我們首先基于信息論中的熵最大化原理推導了分類和KD中涉及溫度的softmax函數。這意味著學生和教師的溫度可以是不同的,并且樣本明智地不同。
分類中的Softmax推導
可以證明分類中的softmax函數在概率歸一化條件下和信息論中狀態期望的約束是熵最大的唯一解。該推導在置信度校準中也被利用來制定溫度標度。假設我們有如下約束熵最大化優化:
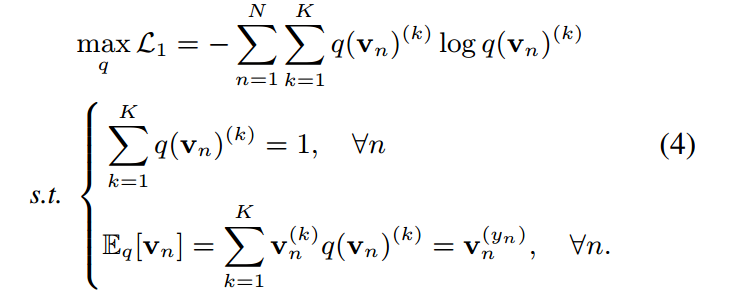
第一個約束由于對離散概率密度的要求而成立,第二個約束控制了分布的范圍,使模型能夠準確地預測目標類。設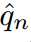 為one-hot硬概率分布,其值除目標指標
為one-hot硬概率分布,其值除目標指標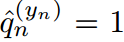 外均為0。第二個約束實際上是
外均為0。第二個約束實際上是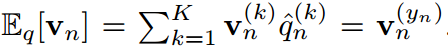 。這相當于使模型預測正確的標簽
。這相當于使模型預測正確的標簽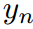 。應用拉格朗日乘子
。應用拉格朗日乘子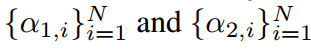 ,得到:
,得到:
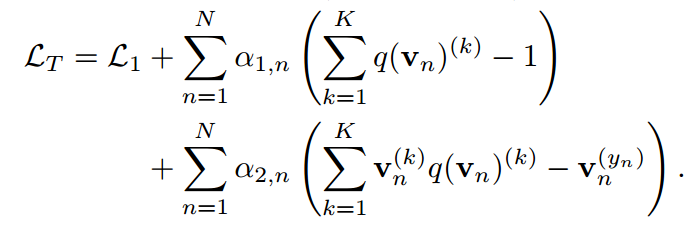
對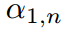 和
和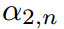 求偏導,得到約束條件。相反,對
求偏導,得到約束條件。相反,對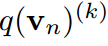 求導得到:
求導得到:
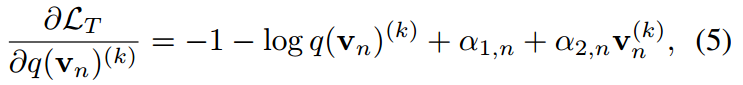
通過使導數為0得到解:
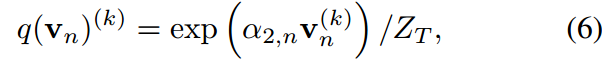
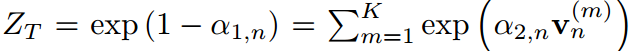 是配分函數滿足歸一化條件。
是配分函數滿足歸一化條件。
KD中的softmax推導
根據這一思想,我們定義了一個熵最大化問題來表示KD中的soft最大值。給定一個訓練有素的教師及其預測,我們有預測學生的目標函數如下:
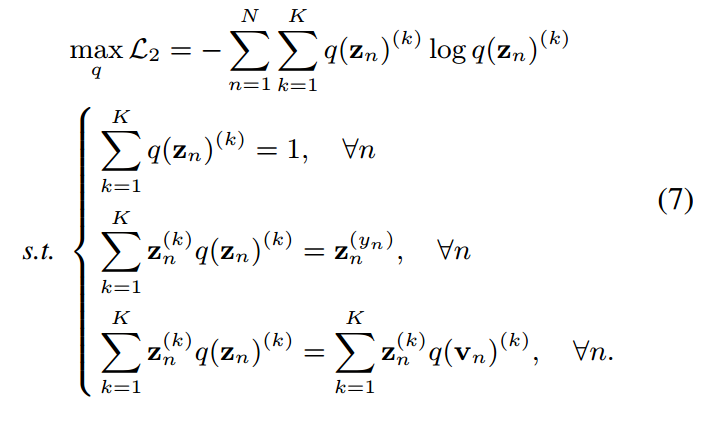
通過應用拉格朗日乘子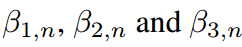
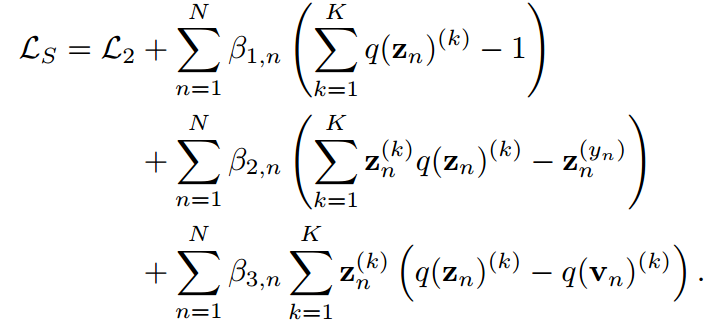
對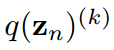 求導得到
求導得到
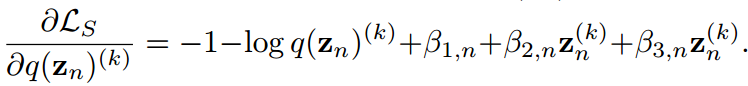
假設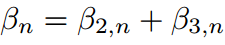 為簡單起見,它給出:
為簡單起見,它給出:
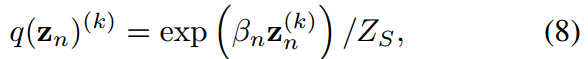
其中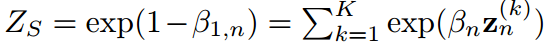 由于概率密度的歸一化條件成立。式8中的公式與式6結構相同。
由于概率密度的歸一化條件成立。式8中的公式與式6結構相同。
不同的溫度
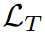 對
對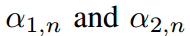 的偏導數分別指向Eq.4中的兩個約束,并且約束與
的偏導數分別指向Eq.4中的兩個約束,并且約束與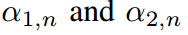 無關。類似的情況也適用于式7.因此,不能給出它們的顯示表達式,因此可以手動定義它們的值。如果設
無關。類似的情況也適用于式7.因此,不能給出它們的顯示表達式,因此可以手動定義它們的值。如果設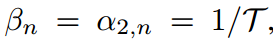 ,則式6和式8轉化為涉及學生和教師共同溫度的KD表達式。
,則式6和式8轉化為涉及學生和教師共同溫度的KD表達式。
當時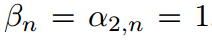 ,公式恢復到分類中常用的傳統softmax函數。最終,我們可以選擇
,公式恢復到分類中常用的傳統softmax函數。最終,我們可以選擇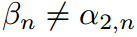 ,這表明教師和學生可以有不同的溫度。
,這表明教師和學生可以有不同的溫度。
明智的選取不同的溫度
通常為所有樣本定義一個全局溫度。即對于任意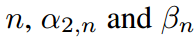 被定義為恒定值。相反,由于缺乏對它們的限制,它們可能在不同的樣本中有所不同。選擇一個全局常數作為溫度缺乏依據。因此,允許采用按樣本變化的溫度。
被定義為恒定值。相反,由于缺乏對它們的限制,它們可能在不同的樣本中有所不同。選擇一個全局常數作為溫度缺乏依據。因此,允許采用按樣本變化的溫度。
共用溫度的缺點
在本節中,我們展示了傳統KD管道中共享溫度設置的兩個缺點。我們首先通過引入兩個超參數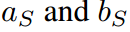 ,將公式8中的softmax用一般公式重寫:
,將公式8中的softmax用一般公式重寫:
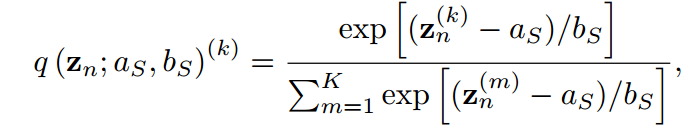
其中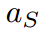 可以消去并且不違反等式。當
可以消去并且不違反等式。當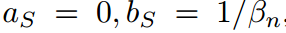 時,會得到公式8中的特殊情況。通過引入
時,會得到公式8中的特殊情況。通過引入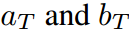 ,可以得到教師情況下的類似方程。
,可以得到教師情況下的類似方程。
對于一個最終得到的很好的蒸餾學生,我們假設KL散度損失達到最小,并且預測教師的密度匹配能力,即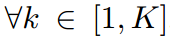 ,
,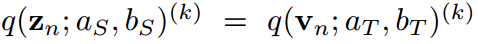 。那么對于任意一對指標
。那么對于任意一對指標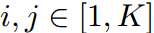 ,很容易得到:
,很容易得到:
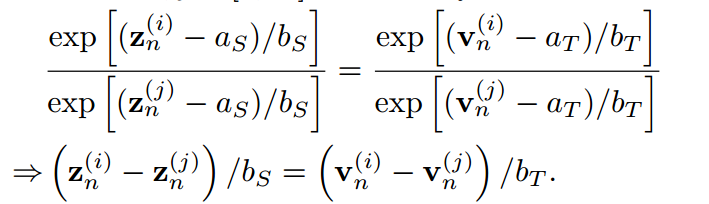
通過對j從1到K求和,我們得到:
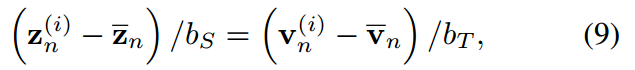
其中,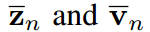 分別為學生和教師logit向量的均值,即
分別為學生和教師logit向量的均值,即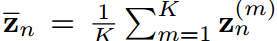 ,(
,(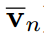 類似)通過等式9對i從1到K的平方求和,我們可以得到:
類似)通過等式9對i從1到K的平方求和,我們可以得到:
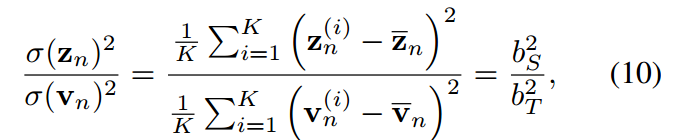
是輸入向量標準差的函數。從公式9到10中,我們可以描述一個受過良好訓練的學生在loigt移位和方差匹配方面的兩個屬性。
Logit shift
由式(9)可知,在傳統的共享溫度( )設置下,學生和教師在任意指標上的對數之間存在恒定的位移,即:
)設置下,學生和教師在任意指標上的對數之間存在恒定的位移,即:
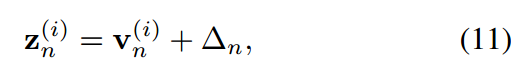
其中,可以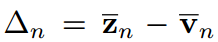 認為是第n個樣本的常數。這意味著在傳統的KD方法中,學生被迫嚴格模仿教師轉移的logit。考慮到模型大小和容量的差距,學生可能無法像老師那樣產生廣泛的logit范圍。相比之下,當學生的Logit排名與教師匹配時,即給定對教師Logit進行排序的指標
認為是第n個樣本的常數。這意味著在傳統的KD方法中,學生被迫嚴格模仿教師轉移的logit。考慮到模型大小和容量的差距,學生可能無法像老師那樣產生廣泛的logit范圍。相比之下,當學生的Logit排名與教師匹配時,即給定對教師Logit進行排序的指標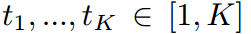 ,使得
,使得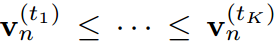 ,則
,則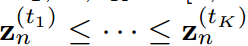 成立。logit關系是使學生和教師一樣善于預測基本知識。因此,這種logit變化是基于傳統KD管道的副作用,并且會迫使學生產生不必要的困難結果。
成立。logit關系是使學生和教師一樣善于預測基本知識。因此,這種logit變化是基于傳統KD管道的副作用,并且會迫使學生產生不必要的困難結果。
方差匹配
從公式10中,我們得出結論,學生和教師的溫度之比等于他們的預測對數的標準差之比,即:
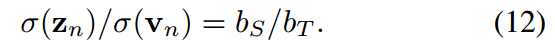
在vanillaKD的溫度共享設置中,學生被迫預測logit,使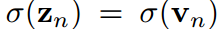 。這是另一個限制學生預測對數標準差的。相反,由于超參數來自拉格朗日乘法器,并且可以靈活調整,我們可以定義
。這是另一個限制學生預測對數標準差的。相反,由于超參數來自拉格朗日乘法器,并且可以靈活調整,我們可以定義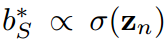 和
和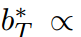
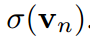 。這樣,公式12中的等式總是成立的。
。這樣,公式12中的等式總是成立的。
Logits標準化
因此,為了打破這兩個束縛,我們建議將超參數分別設置為其對數的均值和加權標準差,即:
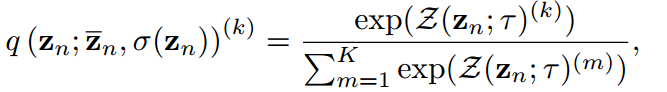
其中,Z為算法中的Z-score函數。教師logit的情況與此類似,略去。在教師模型和學生模型中引入并共享一個基礎溫度T。Z-score標準化至少有4個有利的性質,即0均值、有限標準差、單調性和有界性。
0均值
標準化向量的均值很容易被證明為0.在以前的工作中,假設平均值為0,并且通常在經驗上違反。相反,Z-score函數本質上保證平均值為0。
有限標準差
加權Z-score輸出的標準差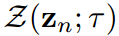 可以表示為1/T。這個性質使標準化的學生和教師logit對數映射到一個相同的高斯分布,平均值為0,標準差確定。表轉化的映射是多對一的,這意味著它的反向是不確定的。因此,原始學生logit向量
可以表示為1/T。這個性質使標準化的學生和教師logit對數映射到一個相同的高斯分布,平均值為0,標準差確定。表轉化的映射是多對一的,這意味著它的反向是不確定的。因此,原始學生logit向量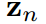 的方差和取值范圍不受限制。
的方差和取值范圍不受限制。
單調性
很容易證明Z-score是一個線性變換函數,因此這是單調函數。這種屬性確保轉換后的學生logit與原始logit保持相同的排名。因此,教師logit中必要的內在關系得以保留并轉移給學生。
有界性
標準化的對數可以在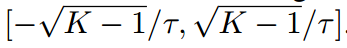 范圍內表示。與傳統KD相比,可以控制logit范圍,避免指數值過大。為此,我們定義了一個基本溫度來控制范圍。
范圍內表示。與傳統KD相比,可以控制logit范圍,避免指數值過大。為此,我們定義了一個基本溫度來控制范圍。
所提出的logit標準化預處理偽代碼在算法2中給出。
Toy Case
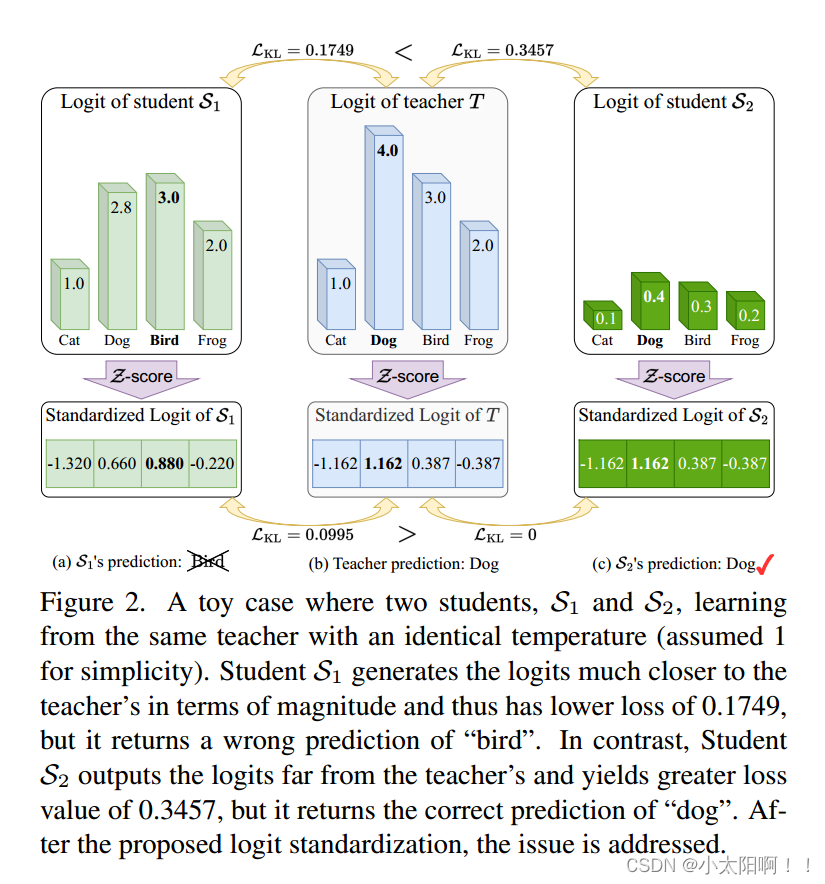
圖2展示了一個典型的案例,其中傳統的基于logit的共享溫度KD設置可能會導致對學生成績的不真實評估。第一個學生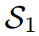 預測的對數在量級上更接近教師T,而第二個學生
預測的對數在量級上更接近教師T,而第二個學生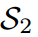 保留了與老師相同的固有對數關系。因此,的KL散度損失較低,為0.1749,明顯優于第二位學生
保留了與老師相同的固有對數關系。因此,的KL散度損失較低,為0.1749,明顯優于第二位學生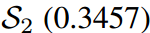 。然而,
。然而,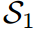 對“Bird”的預測是錯誤的,而
對“Bird”的預測是錯誤的,而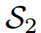 對”dog“的預測是正確的,這與損失對比是矛盾的。通過應用我們的Z分數,所有logit都被重新縮放,并且在評估中強調logit之間的關系而不是它們的大小。即
對”dog“的預測是正確的,這與損失對比是矛盾的。通過應用我們的Z分數,所有logit都被重新縮放,并且在評估中強調logit之間的關系而不是它們的大小。即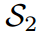 的損失為0,遠好于
的損失為0,遠好于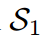 的0.0995,這與預測到的預測是一致的。
的0.0995,這與預測到的預測是一致的。


技術)




)





)


)


