- 引言與研究背景
全焊接球閥的重要性：廣泛應用于石油、天然氣、化工等長輸管道和關鍵裝置，其安全性、密封性和耐久性至關重要。閥體一旦發生焊接缺陷，可能導致災難性后果。
焊接工藝的挑戰：焊接是一個涉及電、熱、力、冶金的復雜瞬態過程。工藝參數（如電流、電壓、焊接速度、坡口形式、層間溫度等）直接影響殘余應力、變形、微觀組織和力學性能。
傳統方法的局限性：
試驗法：通過“試錯”進行工藝評定，成本高昂、周期長、且難以找到全局最優解。
數值模擬法（如有限元分析FEA）：雖然能詳細模擬焊接過程，但計算量極大，單次模擬可能耗時數小時甚至數天，不適用于需要大量迭代的優化過程。
研究必要性：因此，開發一種高效、高精度的優化策略，以最少的成本獲得最優焊接工藝參數，具有重大的工程和經濟價值。
- 核心方法與技術概述
本研究的核心是用計算成本極低的近似模型替代計算成本高昂的有限元仿真，并采用高效的混合優化算法在近似模型上進行尋優。
2.1 組合近似模型（Ensemble of Surrogate Models）
目的：克服單一近似模型可能存在的精度不足和泛化能力差的問題。
常用模型：
克里金模型（Kriging）：擅長插值，能提供預測誤差估計，適用于非線性程度高的問題。
徑向基函數模型（RBF）：對非線性問題有很好的擬合能力。
多項式響應面模型（PRS）：結構簡單，適用于低非線性問題。
組合策略：采用加權平均的方法，將多個單一近似模型的預測結果進行整合。權重可以根據每個模型在驗證集上的表現（如留一法交叉驗證誤差）動態分配。公式可表示為：
Y_ensemble = Σ (w_i * Y_i)
，其中
Σ w_i = 1
。
優勢：綜合各模型優點，提高預測精度和魯棒性。
2.2 IPSO-GA 混合優化算法（Improved PSO-GA）
粒子群算法（PSO）：優點在于全局搜索能力強、收斂速度快，但后期容易陷入局部最優。
遺傳算法（GA）：優點在于通過交叉、變異操作保持種群多樣性，局部精細搜索能力較強，但收斂速度較慢。
IPSO-GA改進策略：
改進PSO（IPSO）：引入慣性權重遞減策略、收縮因子等，平衡全局和局部搜索能力。
混合機制：在IPSO算法運行后，將PSO種群中較優的個體作為GA的初始種群。
協同進化：利用GA的交叉、變異操作對PSO的輸出結果進行深度挖掘，避免早熟收斂，找到全局最優解。
優勢：結合了PSO的快速收斂性和GA的強大探索能力，全局優化性能更優。
- 技術路線與實施方案
第一階段：問題定義與數據采樣
確定優化目標：例如，最小化焊接殘余應力（特別是環向應力）、最小化焊接變形、或實現多目標優化。
識別設計變量：確定關鍵的焊接工藝參數，如：電流（I）、電壓（U）、焊接速度（V）、預熱溫度（T_pre）、道間溫度（T_inter）等。
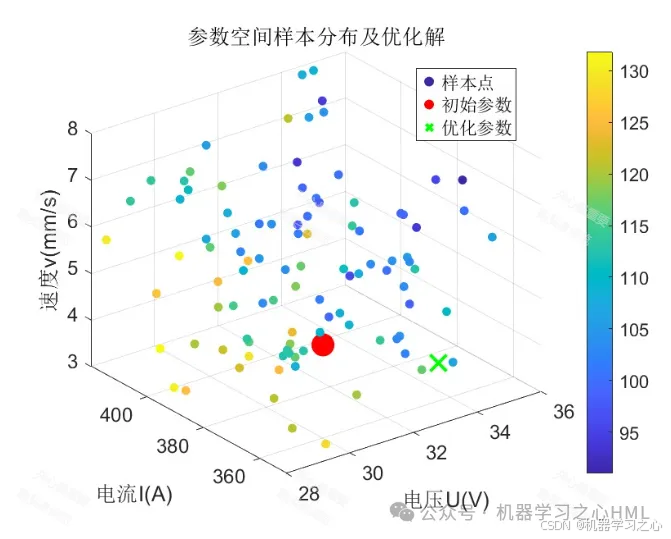
設計實驗（DOE）：采用拉丁超立方采樣（LHS） 在設計空間內生成有限數量（如50-100個）的樣本點。LHS能夠保證樣本點均勻分布，最大限度地代表整個設計空間。
第二階段：高保真有限元計算
運行樣本點仿真：將第一階段生成的樣本點對應的工藝參數輸入有限元模型，進行計算，獲取每個樣本點對應的目標響應值（如最大應力、變形量）。
數據收集：整理形成
[輸入變量，輸出響應]
的數據集，用于構建近似模型。
第三階段：構建與驗證組合近似模型
數據集劃分：將數據集隨機分為訓練集（80%）和測試集（20%）。
構建單一近似模型：分別用訓練集數據構建Kriging、RBF、PRS等模型。
模型驗證與加權：使用測試集計算各模型的預測精度（常用R2、RMSE等指標）。根據精度指標為每個模型分配權重，構建最終的組合近似模型。
驗證組合模型：確保組合模型的預測精度滿足要求（R2 > 0.9），方可替代昂貴的FEA模型。
第四階段：IPSO-GA算法優化
設定算法參數：設置IPSO和GA的種群大小、迭代次數、交叉率、變異率等。
運行優化：將組合近似模型作為目標函數，運行IPSO-GA算法進行尋優。算法在近似模型上評估 millions of次，而實際計算成本極低。
獲取最優解：算法收斂后，輸出一組或多組最優的工藝參數組合。
第五階段：驗證與結論
FEA驗證：將優化算法得到的最優工藝參數代入原始的高保真有限元模型中進行一次驗證計算。
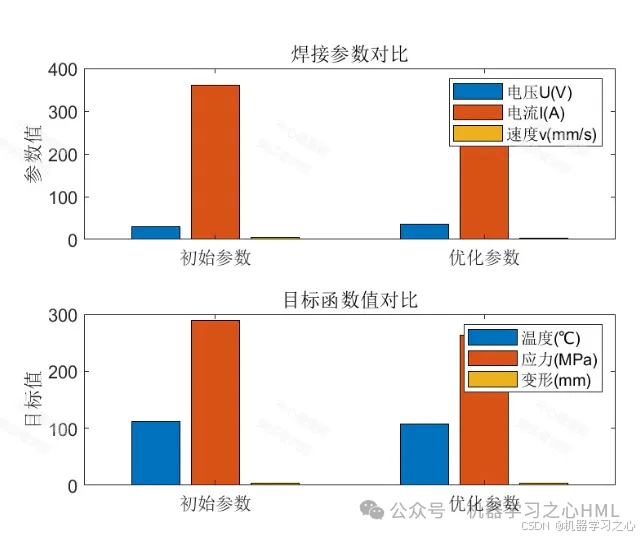
結果對比：對比優化前后的應力、變形等結果，量化優化效果。
得出結論：總結該方法的有效性、優勢和實用價值。
- 總結
本研究通過將組合近似模型與IPSO-GA智能優化算法相結合，構建了一個強大的數字化優化平臺。該平臺能夠以極低的計算成本，對全焊接球閥的焊接工藝參數進行高效全局優化，顯著提升產品質量和可靠性，同時大幅降低研發成本和周期，具有重要的理論意義和工程應用前景。
 （三）)
