目錄
一、實驗
1.1 數據集
1.2 基線算法
1.3 評估指標
1.4 參數設置
1.5 實驗效果
1.5.1 網絡重構
1.5.1.1 方法性能優勢
1.5.1.2 特定數據集表現
1.5.1.3?模型對比分析
1.5.1.4?鄰近性重要性驗證
1.5.2 多標簽分類
1.5.3 鏈路預測
1.5.4網絡可視化的應用
1.6 參數敏感性分析
二、?結論
圖神經系列概覽:圖神經網絡分享系列-概覽-CSDN博客
承接上一篇文章,繼續分享:圖神經網絡分享系列-SDNE(Structural Deep Network Embedding) (二)-CSDN博客
一、實驗
在本節中,我們通過多個真實數據集和應用對所提出的方法進行評估。實驗結果表明,相較于基線方法,該方法取得了顯著提升。
1.1 數據集
為全面評估表征方法的有效性,實驗采用五個網絡數據集,包括三個社交網絡、一個引文網絡和一個語言網絡,覆蓋三種實際應用場景:多標簽分類、鏈接預測及可視化。根據各數據集特性,針對每類應用選取一個或多個數據集進行性能評估,具體描述如下。
- BLOGCATALOG [27]、FLICKR [27] 和 YOUTUBE [28]:它們是線上用戶的社交網絡。每個用戶至少被標注為一個類別。BLOGCATALOG 共有 39 個不同類別,FLICKR 有 195 個類別,YOUTUBE 有 47 個類別。這些類別可作為每個頂點的真實標簽,因此可用于多標簽分類任務的評估。
- ARXIV GR-QC [16]:這是一個論文合作網絡,涵蓋 arXiv 中廣義相對論和量子宇宙學領域的論文。在該網絡中,頂點代表作者,邊表示作者曾在 arXiv 上合作撰寫過科學論文。由于缺乏頂點類別信息,該數據集用于鏈接預測任務。
- 20-NEWSGROUP:該數據集包含約 20000 篇新聞組文檔,每篇文檔被標記為 20 個不同組別之一。使用詞項的 TF-IDF 向量表示文檔,并以余弦相似度衡量文檔間相似性。基于此類相似性可構建網絡。選取標注為 comp.graphics、rec.sport.baseball 和 talk.politics.guns 的文檔進行可視化任務。
在加權與無權、稀疏與密集、小型與大型網絡上進行實驗,所選數據集能全面反映網絡嵌入方法的特性。具體統計數據見表2。

1.2 基線算法
以下五種方法作為基線算法,其中前四種為網絡嵌入方法,而共同鄰居(Common Neighbor)直接基于網絡結構進行鏈路預測,已被證明是有效的鏈路預測方法[17]。
DeepWalk [21]:采用隨機游走和skip-gram模型生成網絡表示。
LINE [26]:通過分別定義損失函數保留一階或二階近似性,優化后拼接不同階數的表示。
GraRep [4]:擴展至高階近似性,利用奇異值分解(SVD)訓練模型,并直接拼接一階與高階表示。
拉普拉斯特征映射(LE)[1]:通過分解鄰接矩陣的拉普拉斯矩陣生成網絡表示,僅利用一階近似性保留網絡結構。
共同鄰居[17]:僅通過頂點間共同鄰居的數量衡量相似性,僅在鏈路預測任務中作為基線。
1.3 評估指標
在實驗中,針對重構、鏈接預測、多標簽分類和可視化任務,采用以下評估方法:
重構與鏈接預測任務使用precision@k和**平均精度均值(MAP)**進行評估,具體定義如下:
- precision@k:該指標對返回結果中的每個實例賦予相同權重,計算公式為:
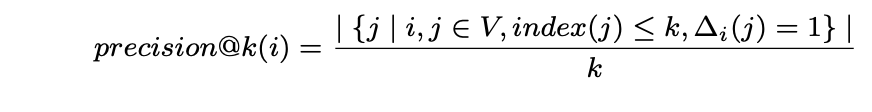
其中,V?為頂點集合,index(j)?表示第j個頂點的排序索引,?i(j) = 1?用于標識頂點vi與vj之間存在連邊關系。
- Mean Average Precision (MAP) 是一種具有良好區分度和穩定性的評價指標。相較于 precision@k,它更關注返回結果中靠前排序項的表現。其計算方法如下:
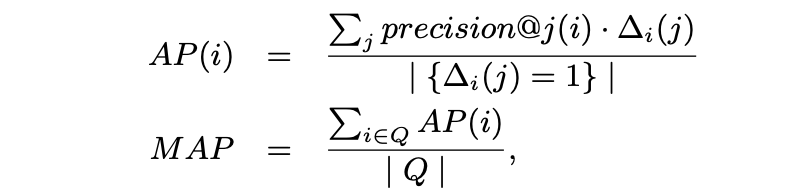
其中 Q 表示查詢集
在多標簽分類任務中,采用與許多其他研究相同的微平均F1(Micro-F1)和宏平均F1(Macro-F1)作為評估指標[27]。具體而言,對于標簽A,用TP(A)、FP(A)和FN(A)分別表示被預測為A的實例中的真正例、假正例和假反例數量。設C為全體標簽集合,微平均F1和宏平均F1定義如下:
- Macro-F1 是一種給予每個類別同等權重的評估指標,其定義如下:
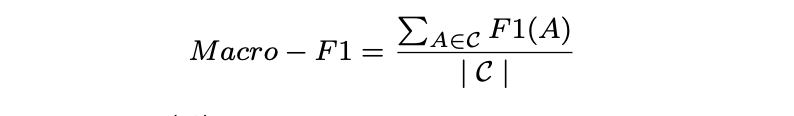
F1(A) 是標簽 A 的 F1 值(F1 分數)
- Micro-F1 是一種對每個實例賦予同等權重的評估指標,其定義如下:

1.4 參數設置

本文提出了一種多層深度結構,層數隨數據集不同而變化。各層維度如表3所示。對于BLOGCATALOG、ARXIV GR-QC和20-NEWSGROUP數據集,神經網絡設置為三層;對于FLICKR和YOUTUBE數據集,則使用四層結構。若采用更深的模型,性能幾乎保持不變甚至可能下降。
方法參數設置
本方法的超參數α、β和ν通過網格搜索在驗證集上進行調優。基線方法的參數均調整為最優值。
LINE參數配置
隨機梯度下降(SGD)的迷你批次大小設為1,初始學習率為0.025。負采樣數量設置為5,總樣本數為100億。依據文獻[26]的建議,LINE模型的最終嵌入向量通過拼接一階和二階表示并做L2歸一化后效果更佳,實驗中遵循此方式生成LINE的結果。
DeepWalk參數配置
窗口大小設為10,隨機游走長度設為40,每個頂點的游走次數設為40。
GraRep參數配置
矩陣轉移步數最大值設為5。
1.5 實驗效果
本節首先評估模型的重建性能,隨后分析不同嵌入方法生成的網絡表征在以下三類經典數據挖掘與機器學習任務中的泛化能力:多標簽分類、鏈接預測及可視化。
1.5.1 網絡重構
在評估所提方法在現實應用中的泛化能力之前,需對不同網絡嵌入方法的網絡重構能力進行基礎評估。此實驗的意義在于,優秀的網絡嵌入方法應確保學習到的嵌入向量能夠保留原始網絡結構。實驗選取語言網絡ARXIV GR-QC和社交網絡BLOGCATALOG作為代表案例。給定一個網絡,分別使用不同嵌入方法學習網絡表示,進而預測原始網絡的鏈接。由于原始網絡中的現有鏈接可作為真實標簽,通過計算訓練集誤差即可評估各方法的重構性能。采用precision@k和MAP作為評估指標,precision@k結果如圖3所示,MAP結果見表4。

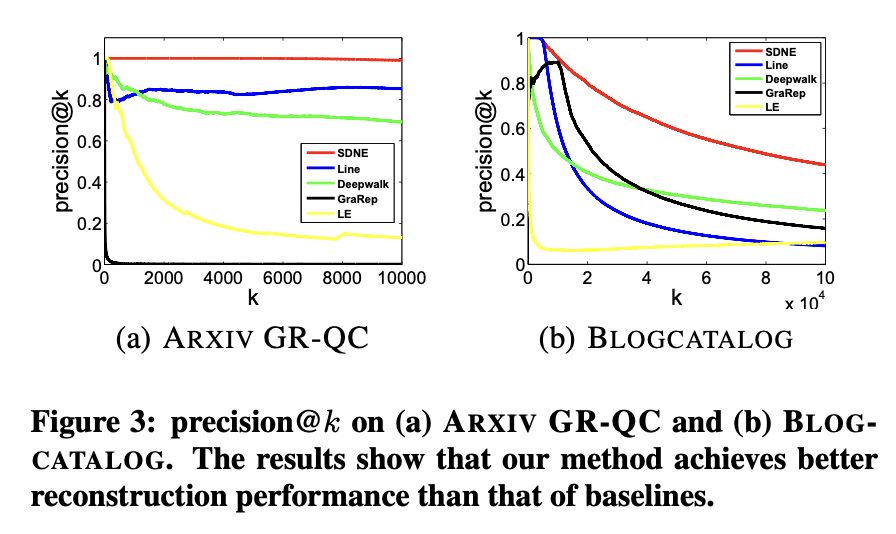
根據研究結果,可得出以下觀察與分析:
1.5.1.1 方法性能優勢
表4數據顯示,該方法在兩個數據集的MAP指標上均顯著超越基線模型。圖3表明隨著k值增大,該方法的precision@k始終維持最高水平,證明該方法能有效保持網絡結構完整性。
1.5.1.2 特定數據集表現
在ARXIV GR-QC網絡中,該方法的precision@k可達100%并在k增至10000時保持該水平。考慮到該數據集總鏈接數為28980,說明該方法能近乎完美地重構原始網絡結構。
1.5.1.3?模型對比分析
盡管SDNE和LINE均利用一階與二階鄰近性保持網絡結構,但SDNE表現更優。可能原因包括:LINE采用的淺層結構難以捕捉底層網絡高度非線性特征;LINE直接拼接兩種鄰近性的表征方式,不如SDNE聯合優化策略高效。
1.5.1.4?鄰近性重要性驗證
SDNE和LINE性能均優于僅使用一階鄰近性的LE算法,證明引入二階鄰近性可顯著提升網絡結構保持效果。
1.5.2 多標簽分類
分類是眾多應用中的核心任務,相關算法和理論已被大量研究[18]。本實驗通過多標簽分類任務評估不同網絡表征方法的有效性。網絡嵌入方法生成的頂點表征作為特征,用于將每個頂點分類至一組標簽中。
具體采用LIBLINEAR工具包[8]訓練分類器。訓練時,隨機抽取部分已標注節點作為訓練數據,其余作為測試集。對于BLOGCATALOG數據集,隨機選取10%至90%的頂點作為訓練樣本,剩余頂點用于測試性能;對于FLICKR和YOUTUBE數據集,則隨機抽取1%至10%的頂點作為訓練樣本,剩余部分用于測試。此外,YOUTUBE數據集中未標注任何類別的頂點被移除。
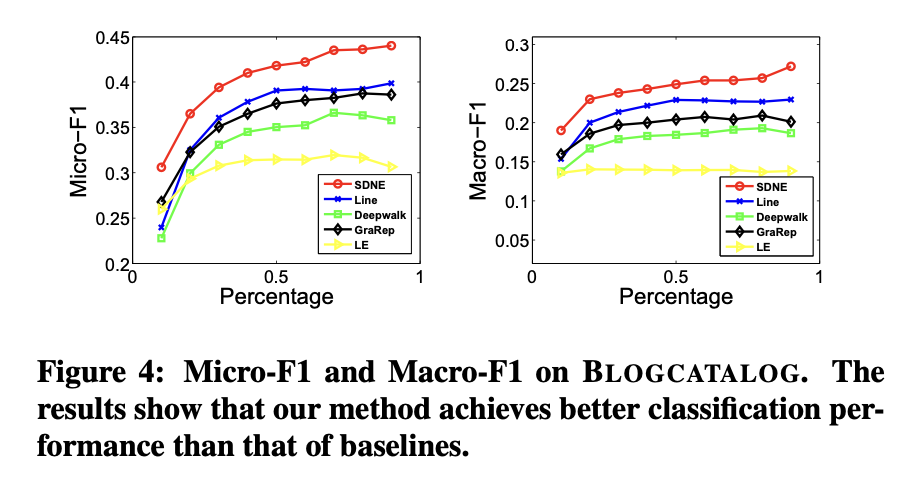
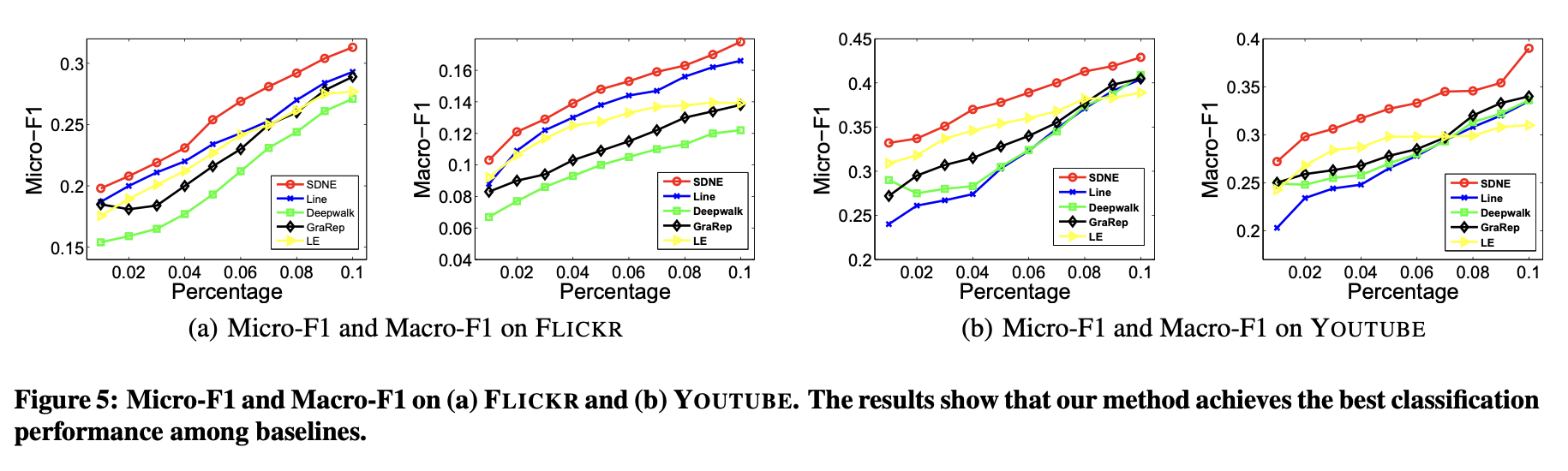
上述過程重復5次,最終報告平均Micro-F1和Macro-F1值。結果分別展示在圖4與圖5中。
關鍵點說明
- 數據劃分:不同數據集的訓練集比例差異(BLOGCATALOG較高,FLICKR/YOUTUBE較低)反映數據規模或標注密度的差異。
- 評估指標:Micro-F1(側重全局統計)和Macro-F1(側重類別均衡)共同衡量分類性能。
- 去噪處理:YOUTUBE中未標注頂點的剔除確保評估有效性。
在圖表4與圖表5中,本方法的曲線始終高于基線方法。這表明相比基線方法,本方法學習到的網絡表征能更有效地泛化至分類任務。
圖表4(BLOGCATALOG數據集)顯示,當訓練數據比例從60%降至10%時,本方法相對于基線方法的性能提升幅度更為顯著。這說明在標注數據有限的情況下,本方法能實現更顯著的性能優勢。這一特性對實際應用尤為重要,因為真實場景中的標注數據通常稀缺。
在多數情況下,DeepWalk在網絡嵌入方法中表現最差。原因有二:其一,DeepWalk缺乏明確的目標函數來捕捉網絡結構;其二,該方法通過隨機游走擴充頂點鄰居關系,這種隨機性會引入大量噪聲(尤其對高度數頂點影響顯著)。
1.5.3 鏈路預測
本節聚焦鏈路預測任務并開展兩項實驗:第一項評估整體性能,第二項分析網絡稀疏性對不同方法性能的影響。實驗數據集采用ARXIV GR-QC。
鏈路預測任務通過隨機隱藏部分已有邊,利用剩余網絡訓練嵌入模型。訓練完成后獲取頂點表示,進而預測未被觀測的邊。與重構任務不同,此任務旨在預測未來可能的連接而非還原現有邊,因此能更好評估不同網絡嵌入方法的可預測性性能。實驗中引入共同鄰居(Common Neighbor)作為基線方法,因其已被證明是有效的鏈路預測策略[17]。
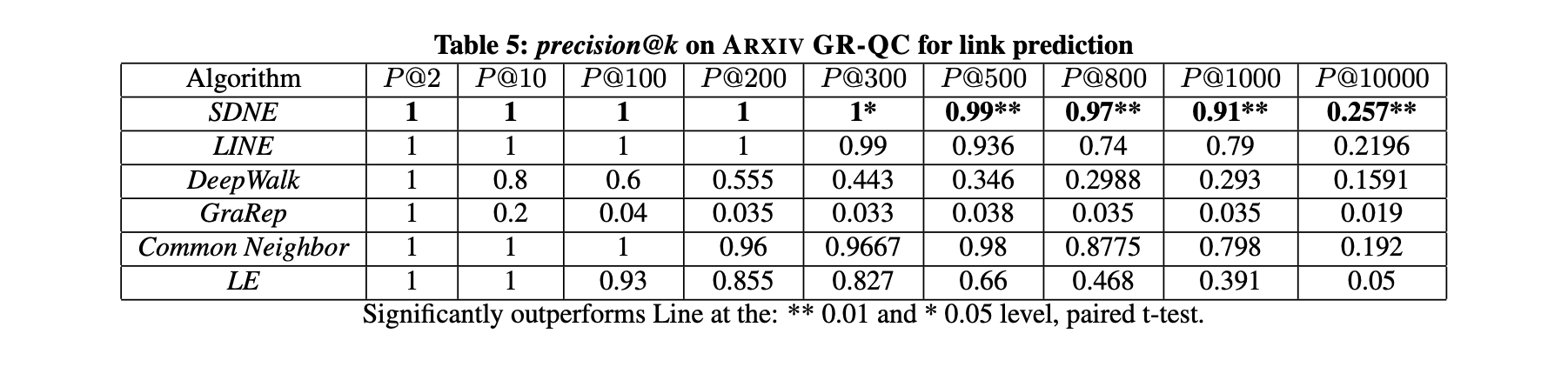
第一項實驗隨機隱藏15%的現有邊(約4000條),采用precision@k作為預測隱藏邊的評估指標。將k值從2逐步增至10000,結果如表5所示(最優性能以加粗標出)。表5的主要觀察與分析如下:
- 結果表明,隨著k值增大,本方法的性能始終優于其他網絡嵌入方法。這表明本方法學習到的表征對新鏈接形成的預測能力更為出色。
- 當k=1000時,本方法的精度仍保持在0.9以上,而其他方法的精度迅速降至0.8以下。這說明本方法在排名靠前的鏈接中能保持較高精度。這一優勢對推薦系統和信息檢索等實際應用尤為重要,因為用戶更關注此類應用中排名靠前的結果。
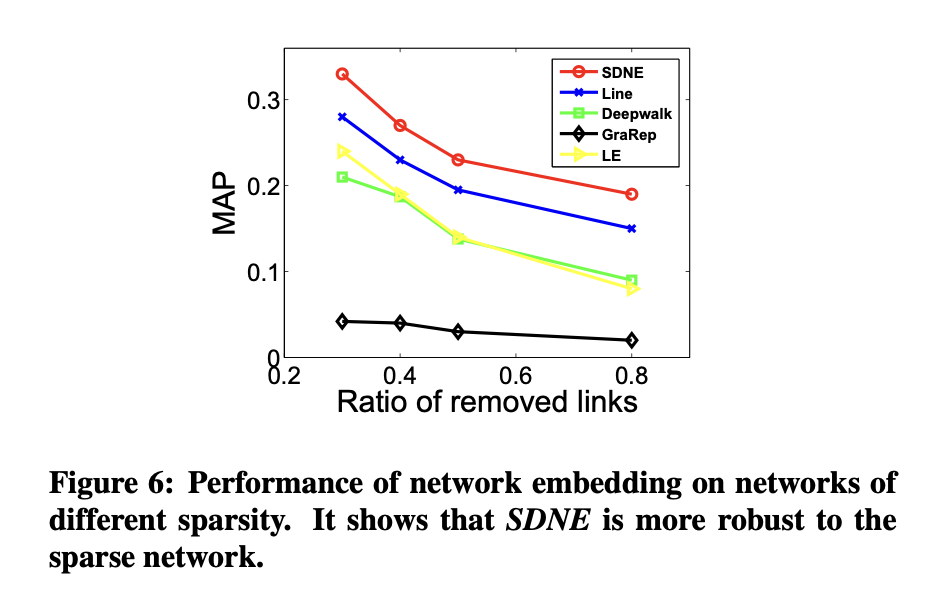
在第二個實驗中,通過隨機移除原始網絡中的部分連接來改變網絡的稀疏性,隨后沿用前述流程比較不同網絡嵌入方法的表現。結果如圖6所示。
稀疏性對方法性能的影響
實驗表明,當網絡越稀疏時,拉普拉斯特征映射(LE)與SDNE、或LE與LINE之間的性能差距會進一步擴大。這說明引入二階鄰近度能夠使學習到的表征對稀疏網絡更具魯棒性。
極端稀疏場景下的表現
即使移除80%的網絡連接,SDNE方法仍顯著優于基線模型。這一結果進一步驗證了SDNE在處理稀疏網絡時的強大能力。
1.5.4網絡可視化的應用
網絡嵌入的另一重要應用是在二維空間中生成網絡的可視化。因此,此處對20-NEWSGROUP網絡學習到的表征進行可視化呈現。采用不同網絡嵌入方法學習到的低維網絡表征作為可視化工具t-SNE的輸入數據。每個新聞組文檔被映射為一個二維向量,進而以二維空間中的點呈現。針對不同類別的標注文檔,其對應點使用不同顏色標記。理想的可視化結果應表現為同色標記點彼此臨近。可視化效果如圖7所示。

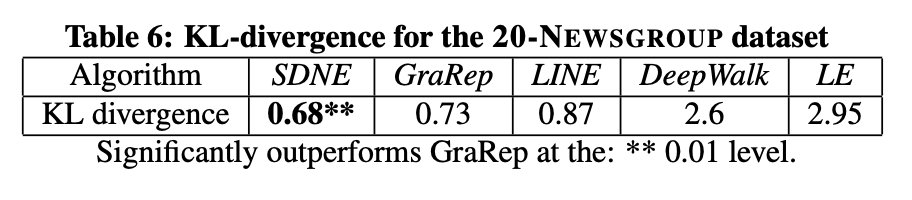
從圖7可以看出,LE和DeepWalk的表現不盡如人意,因為不同類別的數據點相互混雜。LINE方法形成了不同類別的簇群,但在中心區域,不同類別的文檔仍然存在重疊。GraRep的結果相對較好,相同顏色的點形成了獨立的分組,但各組邊界仍不夠清晰。顯然,SDNE在類群分離度和邊界清晰度兩方面的可視化效果最佳。表6的量化數據也進一步驗證了該方法在可視化任務中的優越性。
1.6 參數敏感性分析
本節探討參數敏感性問題,重點評估嵌入維度數量及超參數α、β取值對結果的影響。實驗數據基于ARXIV-GRQC數據集,以Precision@k作為評價指標。
- 嵌入維度數量的選擇
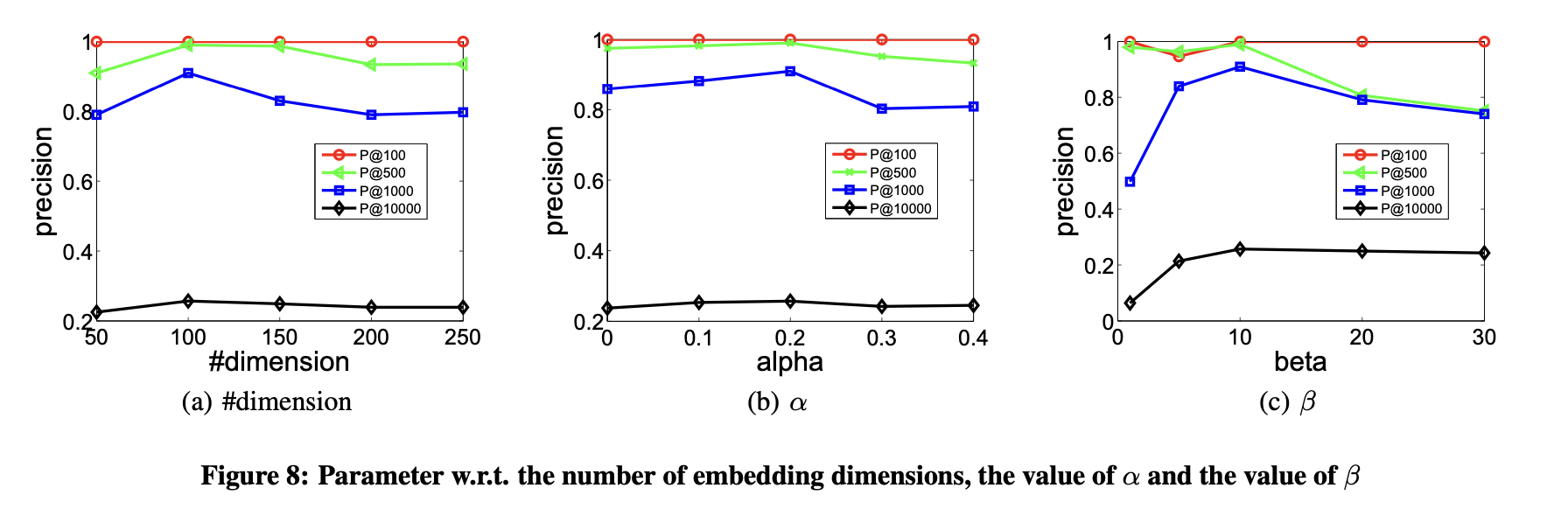
圖8(a)展示了嵌入向量維度對性能的影響。性能隨維度增加提升,因更多維度能編碼更豐富的信息。但當維度持續增加時,性能緩慢下降,原因是過高的維度會引入噪聲導致性能劣化。總體而言,潛在嵌入空間的維度數量需謹慎確定,但本方法對該參數不敏感。
- 一階與二階鄰近性的平衡點分析
研究通過圖8(b)展示了參數α對模型性能的影響。α用于調節頂點間一階鄰近性與二階鄰近性的權重比例。當α=0時,性能完全由二階鄰近性決定;隨著α增大,模型更側重一階鄰近性。圖8(b)顯示,α=0.1和α=0.2的性能優于α=0,表明同時考慮一階和二階鄰近性對網絡嵌入方法捕捉網絡結構至關重要。該結果驗證了兩種鄰近性在表征網絡拓撲時的互補性。
- 重點關注非零元素的重構誤差
實驗最后展示了參數β對模型性能的影響。β控制訓練圖中非零元素的重構權重,其值越大,模型越傾向于優先重構非零元素。圖8(c)結果顯示:當β=1時效果較差,此時模型對網絡中零元素和非零元素賦予同等重構權重。需注意的是,節點間無連邊并不代表兩者不相似,但存在連邊一定表明節點相似性,因此重構零元素會引入噪聲并降低性能。
- 過度強調非零元素的弊端
當β值過大時,性能同樣會下降。原因是模型幾乎完全忽略零元素的重構,傾向于維持任意節點對的相似性。然而,大量零元素實際仍反映節點間的差異性,過度忽略會導致性能退化。
- 實驗結論
該實驗表明:在網絡嵌入任務中,應更關注非零元素的重構誤差,但不可完全放棄對零元素的重構約束。需在二者間取得平衡以獲得最優表現。
二、?結論
本文提出了一種結構深度網絡嵌入方法(Structural Deep Network Embedding, SDNE),用于實現網絡嵌入。該方法通過設計半監督深度模型(含多層非線性函數)捕捉高度非線性的網絡結構。為解決結構保持與稀疏性問題,模型聯合利用一階鄰近度與二階鄰近度刻畫局部與全局網絡結構特征。通過在半監督深度模型中聯合優化這兩類鄰近度,所學表征能夠保持局部-全局結構,并對稀疏網絡具有魯棒性。實驗部分在多個網絡數據集和應用場景中評估了生成的網絡表征效果,結果表明該方法較現有最優技術有顯著提升。未來工作將聚焦于如何為無任何邊連接的新節點學習表征。
本篇論文講解就暫告一斷落,后續會持續更新~
)
)






- 狀態管理與容錯)


)



 異常問題排查實錄)



