二叉樹的前中后序遍歷(迭代法)

題目鏈接：

題目：

解題思路：

代碼：

前序遍歷：

中序遍歷：

后序遍歷：

總結：

題目鏈接：

144. 二叉樹的前序遍歷 - 力扣（LeetCode）

94. 二叉樹的中序遍歷 - 力扣（LeetCode）

145. 二叉樹的后序遍歷 - 力扣（LeetCode）

題目：

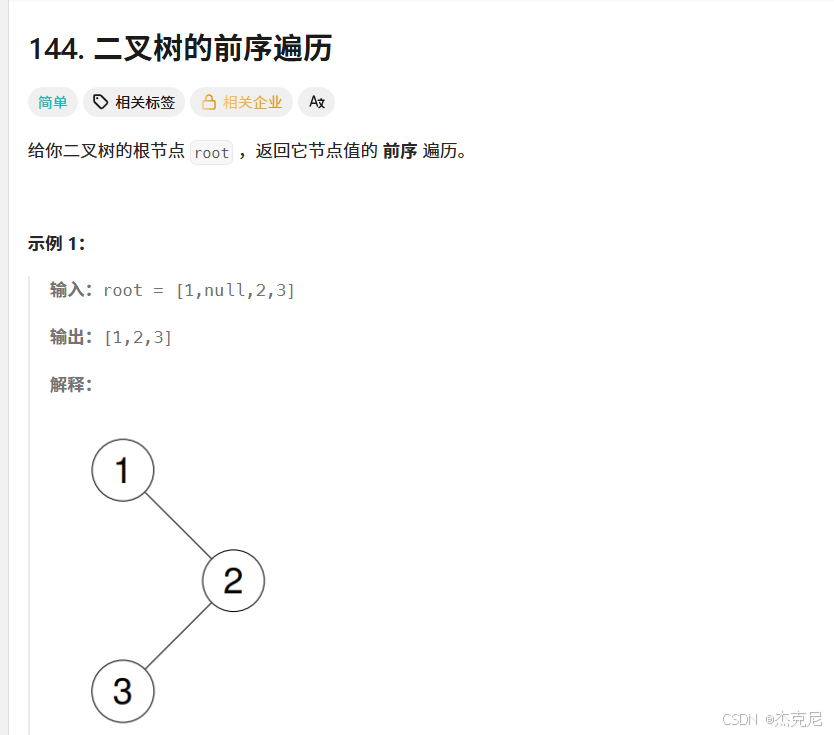
給你二叉樹的根節點 root，返回它節點值的前序遍歷。

示例 1：

輸入：root = [1,null,2,3]
輸出：[1,2,3]

（解釋：二叉樹結構為根節點是 1，1 的右子節點是 2，2 的左子節點是 3，前序遍歷順序為根 - 左 - 右，所以遍歷結果為 1、2、3）

二叉樹的中序遍歷
簡單相關標簽相關企業 Ax
給定一個二叉樹的根節點 root，返回它的中序遍歷。
示例 1:
（圖為二叉樹結構：節點 1 的右子節點是 2，節點 2 的左子節點是 3）
輸入: root = [1,null,2,3]
輸出: [1,3,2]

示例 2:
輸入: root = []
輸出: []

二叉樹的后序遍歷
簡單相關標簽相關企業 Ax
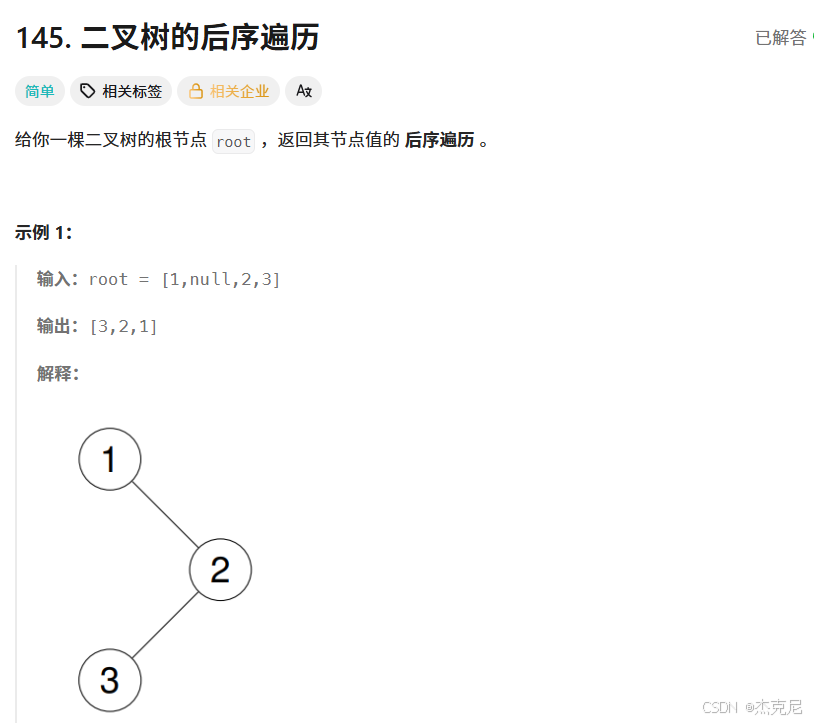
給你一棵二叉樹的根節點 root，返回其節點值的后序遍歷。
示例 1:
輸入: root = [1,null,2,3]
輸出: [3,2,1]
解釋:
（下方有對應二叉樹結構示意圖，根節點是 1，1 的右子節點是 2，2 的左子節點是 3）
?

解題思路：

使用棧和集合即可,還有統一迭代法的形式(后續有)

前序是中左右,但是進棧是中右左

那同理可知后序是左右中,那進棧中左右,再reverse即可

代碼：

前序遍歷：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res=new ArrayList<>();if(root==null) return res;Stack<TreeNode> st=new Stack<>();st.push(root);while(!st.empty()){TreeNode head=st.pop();res.add(head.val);if(head.right!=null) st.push(head.right);if(head.left!=null) st.push(head.left);}return res;}
}

二叉樹前序遍歷的迭代實現：基于棧的深度解析
二叉樹的前序遍歷是樹結構操作中的基礎算法，其 "根→左→右" 的訪問順序在很多場景中都有廣泛應用。除了直觀的遞歸實現外，迭代方式通過手動維護棧結構來模擬遍歷過程，能有效避免遞歸可能帶來的棧溢出問題。本文將詳細解析一個基于棧的二叉樹前序遍歷迭代實現，幫助讀者深入理解其原理、執行流程及優勢。
前序遍歷的核心概念
前序遍歷（Preorder Traversal）是二叉樹的三種基本遍歷方式之一，其核心規則是：對于任意節點，先訪問該節點本身，再遍歷其左子樹，最后遍歷其右子樹，即 "根→左→右" 的訪問順序。每個節點被訪問且僅被訪問一次。

例如，對于二叉樹 [1,null,2,3]（根節點為 1，1 的右子節點為 2，2 的左子節點為 3），其前序遍歷結果為 [1,2,3]，這是按照節點 1→左子樹（空）→右子樹（節點 2→左子樹節點 3→右子樹（空））的順序訪問的結果。
迭代實現的核心思路
遞歸實現利用函數調用棧自然地維護了遍歷順序，而迭代實現則需要手動創建棧來模擬這一過程。前序遍歷的迭代實現核心思路是：

使用棧存儲待訪問的節點
每次彈出棧頂節點并訪問（加入結果列表）
按照 "右子節點→左子節點" 的順序將彈出節點的子節點入棧（因為棧是后進先出結構，這樣才能保證左子節點先被訪問）
重復步驟 2-3，直到棧為空

這種方式通過棧的后進先出（LIFO）特性，完美模擬了前序遍歷 "根→左→右" 的訪問順序。
完整代碼實現
下面是二叉樹前序遍歷的迭代實現代碼：

二叉樹前序遍歷的迭代實現
V1
創建時間：19:56
代碼逐行深度解析
1. 二叉樹節點定義
代碼開頭定義了二叉樹節點的結構：

java
運行
/**
?* Definition for a binary tree node.
?* public class TreeNode {
?* ? ? int val;
?* ? ? TreeNode left;
?* ? ? TreeNode right;
?* ? ? TreeNode() {}
?* ? ? TreeNode(int val) { this.val = val; }
?* ? ? TreeNode(int val, TreeNode left, TreeNode right) {
?* ? ? ? ? this.val = val;
?* ? ? ? ? this.left = left;
?* ? ? ? ? this.right = right;
?* ? ? }
?* }
?*/

這個類定義了二叉樹的基本構成單元，包含：

val：節點存儲的整數 value
left：指向左子節點的引用
right：指向右子節點的引用
三個構造方法：分別用于創建不同狀態的節點

所有二叉樹操作都基于這個節點結構，理解它是掌握樹遍歷的基礎。
2. 初始化結果列表
java
運行
List<Integer> res = new ArrayList<>();

創建一個 ArrayList 實例 res 用于存儲遍歷過程中收集的節點值。選擇 ArrayList 是因為它在添加元素和隨機訪問時性能優良，適合存儲有序的遍歷結果。
3. 處理空樹情況
java
運行
if (root == null) return res;

這是一個重要的邊界條件處理。當輸入的根節點為 null 時（表示空樹），直接返回空的結果列表，避免后續不必要的操作。
4. 初始化棧并推入根節點
java
運行
Stack<TreeNode> st = new Stack<>();
st.push(root);

創建一個 Stack 實例 st，用于存儲待訪問的節點。棧的特性（后進先出）是實現前序遍歷的關鍵。
將根節點 root 推入棧中，作為遍歷的起始點。
5. 棧循環處理邏輯
java
運行
while (!st.empty()) {
? ? // 彈出棧頂節點并訪問
? ? TreeNode head = st.pop();
? ? res.add(head.val);
? ??
? ? // 右子節點先入棧
? ? if (head.right != null) {
? ? ? ? st.push(head.right);
? ? }
? ??
? ? // 左子節點后入棧
? ? if (head.left != null) {
? ? ? ? st.push(head.left);
? ? }
}

這個循環是迭代實現的核心，只要棧不為空，就持續處理節點，直到所有節點都被訪問。循環內部包含三個關鍵步驟：
5.1 彈出棧頂節點并訪問
java
運行
TreeNode head = st.pop();
res.add(head.val);

彈出棧頂節點 head，這是當前要訪問的節點
將節點值 head.val 加入結果列表 res，完成對該節點的訪問

這一步對應前序遍歷中的 "根" 操作，即先訪問當前節點。
5.2 右子節點入棧
java
運行
if (head.right != null) {
? ? st.push(head.right);
}

將當前節點的右子節點推入棧中（如果存在）。注意這里右子節點先入棧，這是因為棧是后進先出的結構，后續左子節點入棧后會被先彈出訪問，從而保證 "左→右" 的順序。
5.3 左子節點入棧
java
運行
if (head.left != null) {
? ? st.push(head.left);
}

將當前節點的左子節點推入棧中（如果存在）。由于左子節點后于右子節點入棧，根據棧的后進先出特性，左子節點會先被彈出訪問，這就保證了前序遍歷 "根→左→右" 的順序。
6. 返回遍歷結果
java
運行
return res;

當棧為空時，所有節點都已被訪問，結果列表 res 中已按前序遍歷順序存儲了所有節點值，將其返回即可。
算法執行過程演示
為了直觀理解迭代實現的執行流程，我們以示例 root = [1,null,2,3] 為例進行詳細演示：

該二叉樹的結構如下：

plaintext
? ? 1
? ? ?\
? ? ? 2
? ? ?/
? ? 3

執行步驟分解：

初始化 res = []，檢查 root 不為 null
創建棧 st，將 root（節點 1）入棧，st = [1]
進入循環（棧不為空）：
彈出棧頂節點 1，res.add(1) → res = [1]
節點 1 的右子節點是 2，將 2 入棧 → st = [2]
節點 1 的左子節點是 null，不操作
棧現在為 [2]
繼續循環（棧不為空）：
彈出棧頂節點 2，res.add(2) → res = [1,2]
節點 2 的右子節點是 null，不操作
節點 2 的左子節點是 3，將 3 入棧 → st = [3]
棧現在為 [3]
繼續循環（棧不為空）：
彈出棧頂節點 3，res.add(3) → res = [1,2,3]
節點 3 的右子節點是 null，不操作
節點 3 的左子節點是 null，不操作
棧現在為空
循環結束，返回 res = [1,2,3]，與預期結果一致

從執行過程可以清晰看到，通過 "根節點出棧訪問→右子節點入棧→左子節點入棧" 的循環操作，完美實現了 "根→左→右" 的前序遍歷順序。棧的后進先出特性在這里起到了關鍵作用。
算法復雜度分析
時間復雜度
對于包含 n 個節點的二叉樹，每個節點都會被推入棧一次并彈出棧一次，因此入棧和出棧操作的總次數為 O (n)。每個節點的值會被加入結果列表一次，也是 O (n) 操作。因此，整體時間復雜度為 O(n)，其中 n 是二叉樹的節點總數。
空間復雜度
空間復雜度主要來自兩個方面：

棧的存儲空間：在最壞情況下（二叉樹退化為左斜樹，即每個節點只有左子節點），棧需要存儲所有節點，此時空間復雜度為 O(n)；在平均情況下（平衡二叉樹），棧的深度為 log (n)，空間復雜度為 O(log n)。
結果列表：用于存儲遍歷結果的列表需要容納所有 n 個節點的值，因此額外占用 O(n) 的空間。

綜合來看，算法的整體空間復雜度為 O(n)。
迭代實現與遞歸實現的對比
前序遍歷有遞歸和迭代兩種主要實現方式，它們各有優缺點：

實現方式?? ?核心思想?? ?優點?? ?缺點
遞歸實現?? ?利用函數調用棧，按照 "根→左→右" 順序遞歸訪問?? ?代碼簡潔直觀，易于理解和編寫?? ?對于深度極大的樹可能導致棧溢出；函數調用有一定性能開銷
迭代實現?? ?手動維護棧，模擬遞歸過程?? ?避免棧溢出風險；性能開銷較小?? ?代碼相對復雜；需要手動管理棧的操作

遞歸實現的代碼通常更簡潔：

java
運行
public List<Integer> preorderTraversal(TreeNode root) {
? ? List<Integer> res = new ArrayList<>();
? ? preorder(res, root);
? ? return res;
}

private void preorder(List<Integer> res, TreeNode root) {
? ? if (root == null) return;
? ? res.add(root.val);
? ? preorder(res, root.left);
? ? preorder(res, root.right);
}

但迭代實現通過手動控制棧，避免了遞歸調用可能帶來的棧溢出問題，在處理大型二叉樹時更為穩健。
算法的優化與擴展
空間優化思考
當前實現的空間復雜度為 O (n)，在某些場景下可以進一步優化。有一種 Morris 遍歷算法可以實現 O (1) 空間復雜度的前序遍歷，其核心思想是利用樹的空指針建立臨時鏈接，避免使用棧或遞歸。但 Morris 算法實現較為復雜，可讀性較差，通常在對空間有嚴格要求的場景下使用。
擴展到其他遍歷方式
基于棧的迭代思想可以擴展到中序和后序遍歷，只需調整節點訪問和入棧的順序：

中序遍歷：先將左子樹全部入棧，彈出節點時訪問，再處理右子樹
后序遍歷：可以通過兩個棧實現，或通過標記節點是否已訪問來實現

例如，后序遍歷的迭代實現（雙棧法）：

java
運行
public List<Integer> postorderTraversal(TreeNode root) {
? ? List<Integer> res = new ArrayList<>();
? ? if (root == null) return res;
? ??
? ? Stack<TreeNode> s1 = new Stack<>();
? ? Stack<TreeNode> s2 = new Stack<>();
? ? s1.push(root);
? ??
? ? while (!s1.isEmpty()) {
? ? ? ? TreeNode node = s1.pop();
? ? ? ? s2.push(node);
? ? ? ? if (node.left != null) s1.push(node.left);
? ? ? ? if (node.right != null) s1.push(node.right);
? ? }
? ??
? ? while (!s2.isEmpty()) {
? ? ? ? res.add(s2.pop().val);
? ? }
? ? return res;
}
實際應用場景
前序遍歷的迭代實現在實際開發中有廣泛應用：

樹的序列化與反序列化：前序遍歷常用于將樹結構轉換為線性序列（序列化），以及從序列重建樹（反序列化）。
路徑搜索：在從根節點到目標節點的路徑搜索中，前序遍歷可以及早發現目標節點，適合深度優先搜索（DFS）場景。
表達式樹的前綴表達式生成：前序遍歷表達式樹可以得到前綴表達式（波蘭式），這種表達式無需括號即可明確運算順序，適合計算機求值。
語法分析：在編譯器的語法分析階段，前序遍歷抽象語法樹（AST）可用于生成中間代碼。
文件系統遍歷：文件系統通常組織為樹結構，前序遍歷可用于實現深度優先的文件搜索。
總結
本文詳細解析了二叉樹前序遍歷的迭代實現，該實現通過手動維護棧結構，模擬了 "根→左→右" 的訪問順序。核心思路是：彈出棧頂節點并訪問，然后按 "右子節點→左子節點" 的順序將子節點入棧，利用棧的后進先出特性保證遍歷順序。

迭代實現的關鍵要點：

利用棧存儲待訪問的節點
彈出節點時立即訪問（加入結果列表）
右子節點先入棧，左子節點后入棧，確保左子節點先被訪問
循環處理直到棧為空

與遞歸實現相比，迭代實現避免了函數調用棧可能帶來的棧溢出問題，在處理大型二叉樹時更為穩健。理解這種實現方式不僅有助于掌握前序遍歷算法，還能加深對棧數據結構和樹遍歷本質的理解。

在實際應用中，應根據具體場景選擇合適的實現方式：對于代碼簡潔性要求高且樹深度可控的場景，遞歸實現更合適；對于可能處理極深樹的場景，迭代實現更為可靠。掌握前序遍歷的迭代實現，對于深入學習數據結構和算法具有重要意義。

中序遍歷：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res=new ArrayList<>();if(root==null){return res;}Stack<TreeNode> st=new Stack<>();while(root!=null||!st.empty()){if(root!=null){st.push(root);root=root.left;}else{root=st.pop();res.add(root.val);root=root.right;}}return res;}
}

二叉樹中序遍歷的迭代實現：基于棧的深度解析
二叉樹的中序遍歷是樹結構操作中最常用的遍歷方式之一，其 "左→根→右" 的訪問順序在二叉搜索樹（BST）中具有特殊意義 —— 能得到一個遞增的有序序列。除了遞歸實現外，迭代方式通過手動維護棧結構來模擬遍歷過程，能有效避免遞歸可能帶來的棧溢出問題。本文將詳細解析一個基于棧的二叉樹中序遍歷迭代實現，幫助讀者深入理解其原理、執行流程及優勢。

中序遍歷的核心概念
中序遍歷（Inorder Traversal）是二叉樹的三種基本遍歷方式之一，其核心規則是：對于任意節點，先遍歷其左子樹，再訪問該節點本身，最后遍歷其右子樹，即 "左→根→右" 的訪問順序。每個節點被訪問且僅被訪問一次。

例如，對于二叉樹?[1,null,2,3]（根節點為 1，1 的右子節點為 2，2 的左子節點為 3），其中序遍歷結果為?[1,3,2]，這是按照左子樹（1 的左子樹為空）→節點 1→右子樹（2 的左子樹 3→節點 2→2 的右子樹為空）的順序訪問的結果。

迭代實現的核心思路
遞歸實現利用函數調用棧自然地維護了遍歷順序，而迭代實現則需要手動創建棧來模擬這一過程。中序遍歷的迭代實現核心思路是：

使用棧存儲待訪問的節點
先將當前節點的所有左子節點依次入棧，直到沒有左子節點為止
彈出棧頂節點并訪問（加入結果列表）
將當前節點指向彈出節點的右子節點，重復步驟 2-3
當當前節點為 null 且棧為空時，遍歷結束
這種方式通過棧的后進先出（LIFO）特性，完美模擬了中序遍歷 "左→根→右" 的訪問順序。

完整代碼實現
下面是二叉樹中序遍歷的迭代實現代碼：

二叉樹中序遍歷的迭代實現

創建時間：20:04

代碼逐行深度解析
1. 二叉樹節點定義
代碼開頭定義了二叉樹節點的結構：

java

運行

/**
?* Definition for a binary tree node.
?* public class TreeNode {
?* ? ? int val;
?* ? ? TreeNode left;
?* ? ? TreeNode right;
?* ? ? TreeNode() {}
?* ? ? TreeNode(int val) { this.val = val; }
?* ? ? TreeNode(int val, TreeNode left, TreeNode right) {
?* ? ? ? ? this.val = val;
?* ? ? ? ? this.left = left;
?* ? ? ? ? this.right = right;
?* ? ? }
?* }
?*/

這個類定義了二叉樹的基本構成單元，包含：

val：節點存儲的整數 value
left：指向左子節點的引用
right：指向右子節點的引用
三個構造方法：分別用于創建不同狀態的節點
所有二叉樹操作都基于這個節點結構，理解它是掌握樹遍歷的基礎。

2. 初始化結果列表
java

運行

List<Integer> res = new ArrayList<>();
創建一個?ArrayList?實例?res?用于存儲遍歷過程中收集的節點值。選擇?ArrayList?是因為它在添加元素和隨機訪問時性能優良，適合存儲有序的遍歷結果。

3. 處理空樹情況
java

運行

if (root == null) {
? ? return res;
}
這是一個重要的邊界條件處理。當輸入的根節點為?null?時（表示空樹），直接返回空的結果列表，避免后續不必要的操作。

4. 初始化棧
java

運行

Stack<TreeNode> st = new Stack<>();
創建一個?Stack?實例?st，用于存儲待訪問的節點。棧的特性（后進先出）是實現中序遍歷的關鍵。與前序遍歷不同，中序遍歷的棧初始化時并不立即推入根節點，而是在循環中逐步處理。

5. 核心循環邏輯
java

運行

while (root != null || !st.empty()) {
? ? // 左子樹全部入棧
? ? if (root != null) {
? ? ? ? st.push(root);
? ? ? ? root = root.left;
? ? } else {
? ? ? ? // 彈出棧頂節點并訪問
? ? ? ? root = st.pop();
? ? ? ? res.add(root.val);
? ? ? ??
? ? ? ? // 轉向右子樹
? ? ? ? root = root.right;
? ? }
}

這個循環是迭代實現的核心，循環條件是 " 當前節點不為空?或?棧不為空 "，確保所有節點都能被處理。循環內部包含兩個主要分支：

5.1 左子樹入棧分支
java

運行

if (root != null) {
? ? st.push(root);
? ? root = root.left;
}

當當前節點?root?不為空時，執行以下操作：

將當前節點?root?推入棧中（暫不訪問，因為中序遍歷需要先處理左子樹）
將?root?指向其左子節點?root.left
這個過程會持續進行，直到?root?變為?null（即到達左子樹的最左端）。這一步確保了我們先處理所有左子節點，符合中序遍歷 "左" 的要求。

5.2 訪問節點并處理右子樹分支
java

運行

else {
? ? // 彈出棧頂節點并訪問
? ? root = st.pop();
? ? res.add(root.val);
? ??
? ? // 轉向右子樹
? ? root = root.right;
}

當當前節點?root?為?null?時（表示左子樹已處理完畢），執行以下操作：

從棧中彈出棧頂節點，這是當前需要訪問的節點（左子樹已處理完畢）
將節點值?root.val?加入結果列表?res，完成對該節點的訪問（符合中序遍歷 "根" 的要求）
將?root?指向其右子節點?root.right，準備處理右子樹（符合中序遍歷 "右" 的要求）
6. 返回遍歷結果
java

運行

return res;
當循環結束時（當前節點為?null?且棧為空），所有節點都已被訪問，結果列表?res?中已按中序遍歷順序存儲了所有節點值，將其返回即可。

算法執行過程演示
為了直觀理解迭代實現的執行流程，我們以示例?root = [1,null,2,3]?為例進行詳細演示：

該二叉樹的結構如下：

plaintext

? ? 1
? ? ?\
? ? ? 2
? ? ?/
? ? 3
執行步驟分解：

執行左子樹入棧分支：將 1 入棧 →?st = [1]，root 指向 1 的左子節點（null）

執行訪問節點分支：彈出棧頂節點 1 →?st = []，res.add(1)?→?res = [1]
root 指向 1 的右子節點（節點 2）

執行左子樹入棧分支：將 2 入棧 →?st = [2]，root 指向 2 的左子節點（節點 3）

執行左子樹入棧分支：將 3 入棧 →?st = [2,3]，root 指向 3 的左子節點（null）

執行訪問節點分支：彈出棧頂節點 3 →?st = [2]，res.add(3)?→?res = [1,3]
root 指向 3 的右子節點（null）

執行訪問節點分支：彈出棧頂節點 2 →?st = []，res.add(2)?→?res = [1,3,2]
root 指向 2 的右子節點（null）

從執行過程可以清晰看到，通過 "左子樹全部入棧→彈出節點訪問→轉向右子樹" 的循環操作，完美實現了 "左→根→右" 的中序遍歷順序。棧在這里起到了暫存節點的作用，確保了節點按正確順序被訪問。

算法復雜度分析
時間復雜度
對于包含 n 個節點的二叉樹，每個節點都會被推入棧一次并彈出棧一次，因此入棧和出棧操作的總次數為 O (n)。每個節點的值會被加入結果列表一次，也是 O (n) 操作。因此，整體時間復雜度為?O(n)，其中 n 是二叉樹的節點總數。

空間復雜度
空間復雜度主要來自兩個方面：

綜合來看，算法的整體空間復雜度為?O(n)。

迭代實現與遞歸實現的對比
中序遍歷有遞歸和迭代兩種主要實現方式，它們各有優缺點：

實現方式?? ?核心思想?? ?優點?? ?缺點
遞歸實現?? ?利用函數調用棧，按照 "左→根→右" 順序遞歸訪問?? ?代碼簡潔直觀，易于理解和編寫?? ?對于深度極大的樹可能導致棧溢出；函數調用有一定性能開銷
迭代實現?? ?手動維護棧，模擬遞歸過程?? ?避免棧溢出風險；性能開銷較小?? ?代碼相對復雜；需要手動管理棧的操作
遞歸實現的代碼通常更簡潔：

java

運行

public List<Integer> inorderTraversal(TreeNode root) {
? ? List<Integer> res = new ArrayList<>();
? ? inorder(res, root);
? ? return res;
}

private void inorder(List<Integer> res, TreeNode root) {
? ? if (root == null) return;
? ? inorder(res, root.left);
? ? res.add(root.val);
? ? inorder(res, root.right);
}

但迭代實現通過手動控制棧，避免了遞歸調用可能帶來的棧溢出問題，在處理大型二叉樹時更為穩健。

算法的優化與擴展
空間優化思考
當前實現的空間復雜度為 O (n)，在某些場景下可以進一步優化。Morris 遍歷算法可以實現 O (1) 空間復雜度的中序遍歷，其核心思想是利用樹的空指針建立臨時鏈接（線索），避免使用棧或遞歸。但 Morris 算法實現較為復雜，可讀性較差，通常在對空間有嚴格要求的場景下使用。

擴展到其他遍歷方式
基于棧的迭代思想可以擴展到前序和后序遍歷，只需調整節點訪問和入棧的順序：

前序遍歷：訪問節點后，先將右子節點入棧，再將左子節點入棧
后序遍歷：可以通過兩個棧實現，或通過標記節點是否已訪問來實現
例如，前序遍歷的迭代實現：

java

運行

public List<Integer> preorderTraversal(TreeNode root) {
? ? List<Integer> res = new ArrayList<>();
? ? if (root == null) return res;
? ??
? ? Stack<TreeNode> st = new Stack<>();
? ? st.push(root);
? ??
? ? while (!st.empty()) {
? ? ? ? TreeNode node = st.pop();
? ? ? ? res.add(node.val);
? ? ? ? if (node.right != null) st.push(node.right);
? ? ? ? if (node.left != null) st.push(node.left);
? ? }
? ? return res;
}
實際應用場景
中序遍歷的迭代實現在實際開發中有廣泛應用：

總結
本文詳細解析了二叉樹中序遍歷的迭代實現，該實現通過手動維護棧結構，模擬了 "左→根→右" 的訪問順序。核心思路是：先將所有左子節點入棧，彈出節點時訪問，然后轉向右子樹，利用棧的后進先出特性保證遍歷順序。

迭代實現的關鍵要點：

循環條件為 "當前節點不為空或棧不為空"
左子樹全部入棧后再開始訪問節點
訪問節點后轉向其右子樹繼續處理
棧在這里起到暫存節點的作用，確保按正確順序訪問
與遞歸實現相比，迭代實現避免了函數調用棧可能帶來的棧溢出問題，在處理大型二叉樹時更為穩健。理解這種實現方式不僅有助于掌握中序遍歷算法，還能加深對棧數據結構和樹遍歷本質的理解。

在實際應用中，應根據具體場景選擇合適的實現方式：對于代碼簡潔性要求高且樹深度可控的場景，遞歸實現更合適；對于可能處理極深樹的場景，迭代實現更為可靠。掌握中序遍歷的迭代實現，對于深入學習數據結構和算法具有重要意義。

return Collections.reverse(res); Line 34: error: incompatible types: void cannot be converted to List<Integer> return Collections.reverse(res); ^

這個錯誤的原因是?Collections.reverse(res)?方法的返回值類型是?void（沒有返回值），而你的方法聲明需要返回一個?List<Integer>?類型的結果，因此出現了 " 無法將 void 轉換為 List<Integer>" 的類型不匹配錯誤。

Collections.reverse()?方法的作用是原地反轉列表中的元素（直接修改原列表），而不是返回一個新的反轉后的列表。所以正確的用法應該是先調用反轉方法，再返回原列表：

java

運行

// 錯誤寫法
return Collections.reverse(res);

// 正確寫法
Collections.reverse(res); ?// 先原地反轉列表
return res; ? ? ? ? ? ? ? ?// 再返回反轉后的列表

例如，在后序遍歷的迭代實現中，如果你想通過反轉前序遍歷結果來得到后序遍歷結果，正確的代碼應該是：

java

運行

public List<Integer> postorderTraversal(TreeNode root) {
? ? List<Integer> res = new ArrayList<>();
? ? if (root == null) return res;
? ??
? ? Stack<TreeNode> stack = new Stack<>();
? ? stack.push(root);
? ??
? ? // 先進行類似前序遍歷的操作（根→右→左）
? ? while (!stack.isEmpty()) {
? ? ? ? TreeNode node = stack.pop();
? ? ? ? res.add(node.val);
? ? ? ? if (node.left != null) stack.push(node.left); ?// 左子節點后入棧
? ? ? ? if (node.right != null) stack.push(node.right); // 右子節點先入棧
? ? }
? ??
? ? // 反轉結果得到后序遍歷（左→右→根）
? ? Collections.reverse(res);
? ? return res; ?// 返回反轉后的列表
}

總結：Collections.reverse()?是一個修改原對象的方法，沒有返回值，因此不能直接作為返回語句使用，需要分開寫。

后序遍歷：

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res=new ArrayList<>();if(root==null){return res;}Stack<TreeNode> st=new Stack<>();st.push(root);while(!st.empty()){TreeNode node=st.pop();res.add(node.val);if(node.left!=null){st.push(node.left);}if(node.right!=null){st.push(node.right);}}Collections.reverse(res);return res;}
}

二叉樹后序遍歷的迭代實現：基于棧和反轉的深度解析
二叉樹的后序遍歷是樹結構操作中的重要遍歷方式，其 "左→右→根" 的訪問順序在刪除操作、表達式求值等場景中具有特殊價值。后序遍歷的迭代實現相對復雜，但有一種巧妙的方法可以通過修改前序遍歷并反轉結果來高效實現。本文將詳細解析這種基于棧和反轉的后序遍歷迭代實現，幫助讀者深入理解其原理、執行流程及優勢。
后序遍歷的核心概念
后序遍歷（Postorder Traversal）是二叉樹的三種基本遍歷方式之一，其核心規則是：對于任意節點，先遍歷其左子樹，再遍歷其右子樹，最后訪問該節點本身，即 "左→右→根" 的訪問順序。每個節點被訪問且僅被訪問一次。

例如，對于二叉樹 [1,null,2,3]（根節點為 1，1 的右子節點為 2，2 的左子節點為 3），其后序遍歷結果為 [3,2,1]，這是按照左子樹（3）→右子樹（無）→節點 2→右子樹（已處理）→節點 1 的順序訪問的結果。
基于反轉的實現思路
后序遍歷的直接迭代實現需要判斷節點的訪問狀態，邏輯較為復雜。而一種巧妙的替代方案是：

執行一種 modified 前序遍歷，訪問順序為 "根→右→左"
將遍歷結果反轉，得到的就是 "左→右→根" 的后序遍歷結果

這種方法的原理是：

標準前序遍歷：根→左→右
modified 前序遍歷（交換左右子節點入棧順序）：根→右→左
反轉 modified 前序遍歷結果：左→右→根（即后序遍歷）

這種思路將復雜的后序遍歷轉化為相對簡單的前序遍歷加反轉操作，大大簡化了代碼實現。
完整代碼實現
下面是基于這種思路的二叉樹后序遍歷迭代實現代碼：

二叉樹后序遍歷的迭代實現（基于棧和反轉）
V1
創建時間：20:24
代碼逐行深度解析
1. 二叉樹節點定義
代碼開頭定義了二叉樹節點的結構：

這個類定義了二叉樹的基本構成單元，包含：

val：節點存儲的整數 value
left：指向左子節點的引用
right：指向右子節點的引用
三個構造方法：分別用于創建不同狀態的節點

所有二叉樹操作都基于這個節點結構，理解它是掌握樹遍歷的基礎。
2. 初始化結果列表
java
運行
List<Integer> res = new ArrayList<>();

創建一個 ArrayList 實例 res 用于存儲遍歷過程中收集的節點值。選擇 ArrayList 是因為它在添加元素和支持反轉操作時性能優良。
3. 處理空樹情況
java
運行
if (root == null) {
? ? return res;
}

創建一個 Stack 實例 st，用于存儲待訪問的節點。棧的后進先出特性是實現 modified 前序遍歷的關鍵。
將根節點 root 推入棧中，作為遍歷的起始點。
5. 棧循環處理邏輯（modified 前序遍歷）
java
運行
while (!st.empty()) {
? ? // 彈出棧頂節點并訪問
? ? TreeNode node = st.pop();
? ? res.add(node.val);
? ??
? ? // 左子節點先入棧
? ? if (node.left != null) {
? ? ? ? st.push(node.left);
? ? }
? ??
? ? // 右子節點后入棧
? ? if (node.right != null) {
? ? ? ? st.push(node.right);
? ? }
}

這個循環實現了 "根→右→左" 的 modified 前序遍歷，只要棧不為空，就持續處理節點，直到所有節點都被訪問。循環內部包含三個關鍵步驟：
5.1 彈出棧頂節點并訪問
java
運行
TreeNode node = st.pop();
res.add(node.val);

彈出棧頂節點 node，這是當前要訪問的節點
將節點值 node.val 加入結果列表 res，完成對該節點的訪問

這一步對應 modified 前序遍歷中的 "根" 操作，即先訪問當前節點。
5.2 左子節點入棧
java
運行
if (node.left != null) {
? ? st.push(node.left);
}

將當前節點的左子節點推入棧中（如果存在）。注意這里左子節點先入棧，這與標準前序遍歷的入棧順序相反。
5.3 右子節點入棧
java
運行
if (node.right != null) {
? ? st.push(node.right);
}

將當前節點的右子節點推入棧中（如果存在）。由于右子節點后于左子節點入棧，根據棧的后進先出特性，右子節點會先被彈出訪問，這就保證了 modified 前序遍歷 "根→右→左" 的順序。
6. 反轉結果列表
java
運行
Collections.reverse(res);

調用 Collections.reverse() 方法對結果列表進行原地反轉。這一步是將 modified 前序遍歷的 "根→右→左" 結果轉換為后序遍歷的 "左→右→根" 結果的關鍵。

需要注意的是，Collections.reverse() 方法的返回值為 void（無返回值），它直接修改原列表，因此不能直接將其作為返回值使用（如錯誤寫法 return Collections.reverse(res);）。
7. 返回遍歷結果
java
運行
return res;

當反轉完成后，結果列表 res 中已按后序遍歷順序存儲了所有節點值，將其返回即可。
算法執行過程演示
為了直觀理解這種實現的執行流程，我們以示例 root = [1,null,2,3] 為例進行詳細演示：

該二叉樹的結構如下：

plaintext
? ? 1
? ? ?\
? ? ? 2
? ? ?/
? ? 3

執行步驟分解：

初始化 res = []，檢查 root（節點 1）不為 null
創建棧 st，將 root（節點 1）入棧，st = [1]
進入循環（棧不為空）：
彈出棧頂節點 1，res.add(1) → res = [1]
節點 1 的左子節點是 null，不操作
節點 1 的右子節點是 2，將 2 入棧 → st = [2]
棧現在為 [2]
繼續循環（棧不為空）：
彈出棧頂節點 2，res.add(2) → res = [1,2]
節點 2 的左子節點是 3，將 3 入棧 → st = [3]
節點 2 的右子節點是 null，不操作
棧現在為 [3]
繼續循環（棧不為空）：
彈出棧頂節點 3，res.add(3) → res = [1,2,3]
節點 3 的左子節點是 null，不操作
節點 3 的右子節點是 null，不操作
棧現在為空
循環結束，執行 Collections.reverse(res) → res = [3,2,1]
返回 res = [3,2,1]，與預期結果一致

從執行過程可以清晰看到：

modified 前序遍歷得到 [1,2,3]（根→右→左順序）
反轉后得到 [3,2,1]（左→右→根順序），即后序遍歷結果

這種通過修改前序遍歷順序并反轉結果的方法，巧妙地實現了后序遍歷，大大簡化了代碼邏輯。
算法復雜度分析
時間復雜度
對于包含 n 個節點的二叉樹：

每個節點會被推入棧一次并彈出棧一次，入棧和出棧操作的總次數為 O (n)
每個節點的值會被加入結果列表一次，是 O (n) 操作
Collections.reverse() 方法需要遍歷列表一次，是 O (n) 操作

因此，整體時間復雜度為 O(n)，其中 n 是二叉樹的節點總數。
空間復雜度
空間復雜度主要來自三個方面：

棧的存儲空間：在最壞情況下（二叉樹退化為右斜樹，即每個節點只有右子節點），棧需要存儲所有節點，此時空間復雜度為 O(n)；在平均情況下（平衡二叉樹），棧的深度為 log (n)，空間復雜度為 O(log n)。
結果列表：用于存儲遍歷結果的列表需要容納所有 n 個節點的值，因此額外占用 O(n) 的空間。
反轉操作：Collections.reverse() 方法是原地反轉，不需要額外的空間。

綜合來看，算法的整體空間復雜度為 O(n)。
與其他后序遍歷實現的對比
后序遍歷有多種迭代實現方式，主要包括：

實現方式?? ?核心思想?? ?優點?? ?缺點
基于反轉的實現?? ?修改前序遍歷為 "根→右→左"，再反轉結果?? ?代碼簡潔，易于理解和實現?? ?需要額外的反轉操作；修改原列表
單棧標記法?? ?使用棧存儲節點，通過標記判斷節點是否已訪問?? ?無需反轉，直接得到結果?? ?邏輯復雜，需要額外標記
雙棧法?? ?使用兩個棧，第一個棧按 "根→左→右" 入棧，第二個棧存儲彈出元素?? ?思路清晰，無需標記?? ?需要額外的棧空間

單棧標記法的示例代碼：

java
運行
public List<Integer> postorderTraversal(TreeNode root) {
? ? List<Integer> res = new ArrayList<>();
? ? if (root == null) return res;
? ??
? ? Stack<Object[]> stack = new Stack<>();
? ? stack.push(new Object[]{root, false});
? ??
? ? while (!stack.isEmpty()) {
? ? ? ? Object[] entry = stack.pop();
? ? ? ? TreeNode node = (TreeNode) entry[0];
? ? ? ? boolean visited = (boolean) entry[1];
? ? ? ??
? ? ? ? if (visited) {
? ? ? ? ? ? res.add(node.val);
? ? ? ? } else {
? ? ? ? ? ? stack.push(new Object[]{node, true});
? ? ? ? ? ? if (node.right != null) stack.push(new Object[]{node.right, false});
? ? ? ? ? ? if (node.left != null) stack.push(new Object[]{node.left, false});
? ? ? ? }
? ? }
? ? return res;
}

相比之下，基于反轉的實現代碼最為簡潔，易于理解和記憶，是實際開發中常用的后序遍歷實現方式。
實際應用場景
后序遍歷的這種實現方式在實際開發中有廣泛應用：

二叉樹的刪除操作：刪除節點時需要先刪除左右子節點，再刪除當前節點，與后序遍歷順序一致。
計算二叉樹的深度：需要先計算左右子樹深度，再取最大值加 1，適合后序遍歷。
表達式樹求值：后序遍歷表達式樹可以得到后綴表達式（逆波蘭式），適合計算機直接求值。
路徑總和問題：需要遍歷到葉子節點后再計算路徑總和，后序遍歷提供了天然的回溯機制。
資源釋放：在釋放樹形結構的資源時，需要先釋放子節點資源，再釋放父節點資源，與后序遍歷順序一致。
總結
本文詳細解析了二叉樹后序遍歷的一種巧妙迭代實現，該實現通過以下步驟完成：

執行 "根→右→左" 的 modified 前序遍歷（通過調整左右子節點的入棧順序實現）
反轉遍歷結果，得到 "左→右→根" 的后序遍歷結果

這種方法的核心優勢在于將復雜的后序遍歷轉化為相對簡單的前序遍歷加反轉操作，大大簡化了代碼實現。代碼的關鍵要點包括：

左子節點先入棧，右子節點后入棧，確保彈出順序為 "根→右→左"
使用 Collections.reverse() 方法對結果進行原地反轉
注意 Collections.reverse() 無返回值，需先調用再返回原列表

與其他后序遍歷實現相比，這種方法代碼簡潔、易于理解和記憶，是實際開發中推薦的實現方式。理解這種實現不僅有助于掌握后序遍歷算法，還能培養對不同遍歷方式之間聯系的洞察力，為解決更復雜的樹結構問題奠定基礎。

在實際應用中，這種實現方式特別適合對代碼簡潔性要求較高，且樹的規模在可接受范圍內的場景。掌握它對于深入學習數據結構和算法具有重要意義。

總結：

本文系統介紹了二叉樹前序、中序和后序遍歷的迭代實現方法。前序遍歷采用棧結構，按;根→右→左 ;順序入棧；中序遍歷先全部左子樹入棧再訪問節點；后序遍歷則通過修改前序遍歷順序為"根→右→左 ;后反轉結果。三種遍歷時間復雜度均為O(n)，空間復雜度最壞O(n)。與遞歸實現相比，迭代方法避免了棧溢出風險，處理大型樹更穩定。每種遍歷方式都配有詳細代碼解析、執行示例和復雜度分析，并討論了實際應用場景，為掌握樹結構操作提供了系統指導。