引言

本文將從CPU演變的視角逐步推進說明CPU演進過程，同時也會針對計算機數學運算過程中一些常見的錯誤細節進行探討。

CPU如何實現邏輯運算

NMOS和PMOS

CPU是由晶體管構成，在邏輯上我們一般會將其通過電路符號進行抽象，即分為如下三個連接端：

1. 柵級(gate)
2. 源極(source)
3. 漏極(drain)

基于NMOS而言，從語義上來理解，它是消極的MOS管(N即negative)，所以它的電流是逆流而上的，這也就是為什么下圖中寄生二極管(即右邊的箭頭)的朝向是由源極(S)到漏極(D)即通過這樣的導向避免漏極電流無條件從漏極流向源極，從N的語義上理解，因為電流是消極的流向，所以輸出電流也必須付出更大的努力才能導通電源，所以NMOS的規范為：

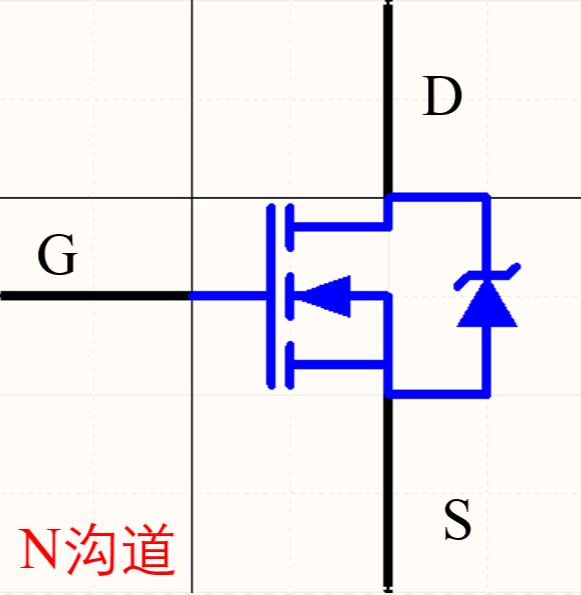
1. 當輸入二進制1時，柵極閉合，電路導通，電流從漏極流向源極
2. 當輸入二進制00時，柵極電源斷開，電路無法導通

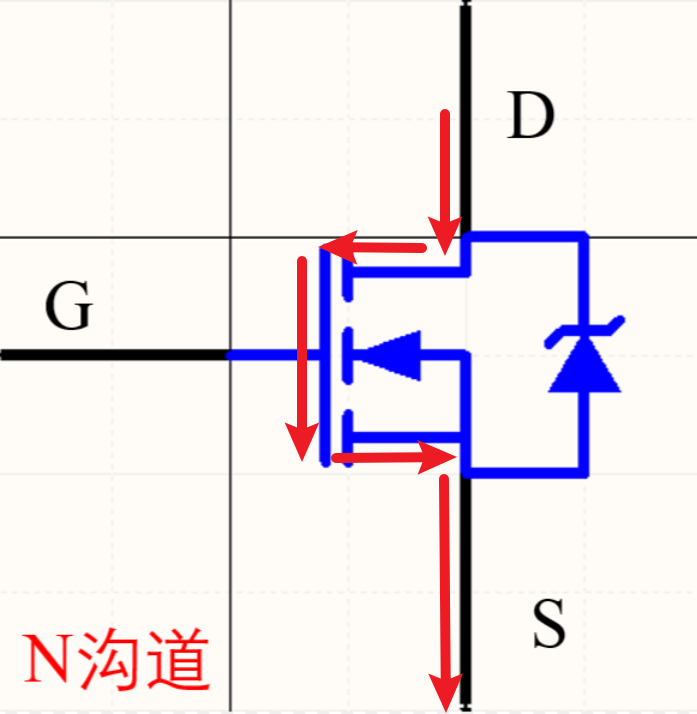
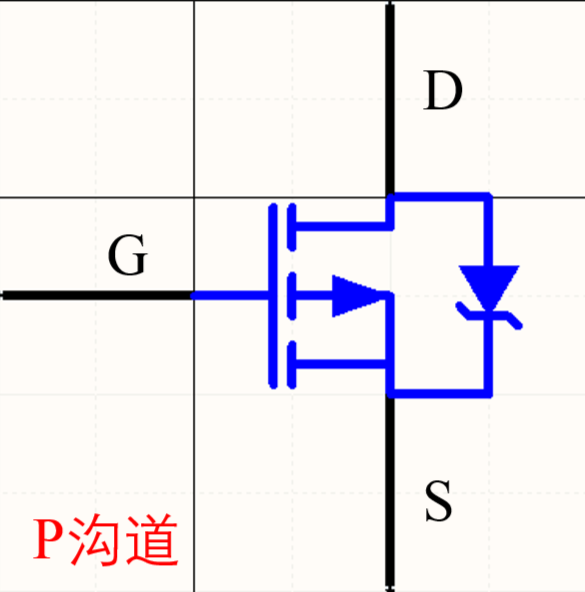
PMOS反之，可以看到寄生二極管從漏極指向源極避免源極無條件流向漏極，因為PMOS是積極的(P即positive)，即無需過多努力即可導通電源，所以其電路運行機制為：

1. 當輸入0時，柵極閉合，電路直接導通，從源極直接流向漏極
2. 當輸入1，柵極斷開，電路無法導通

基于MOS管組合下的邏輯門運算

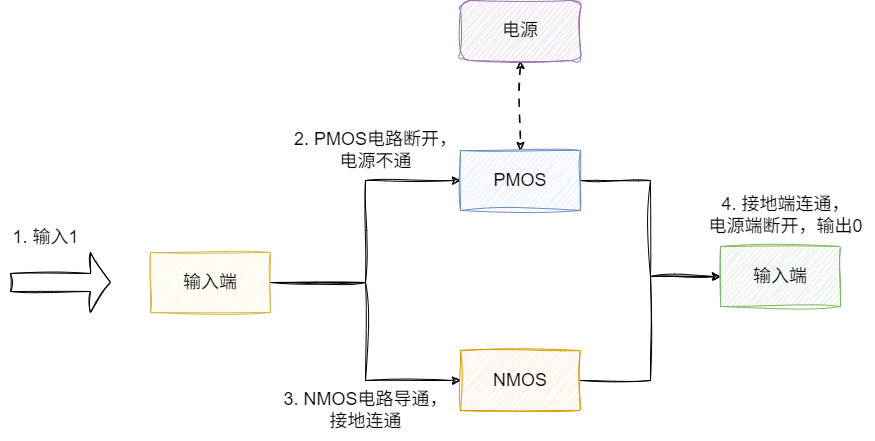
基于上述電路符號的基礎上，我們將二者結合，NMOS接地、PMOS接電源，試想這樣我們輸入數字1：

1. 對于NMOS電源導通，輸出端Y導通，接地連同
2. 對于PMOS電源斷開，與電源端斷開
3. 最終沒有亮起輸出0

同理，我們不妨再嘗試輸入0：

1. 對于NMOS電源斷開
2. 對于PMOS電源導通
3. 電源端導通，輸出1

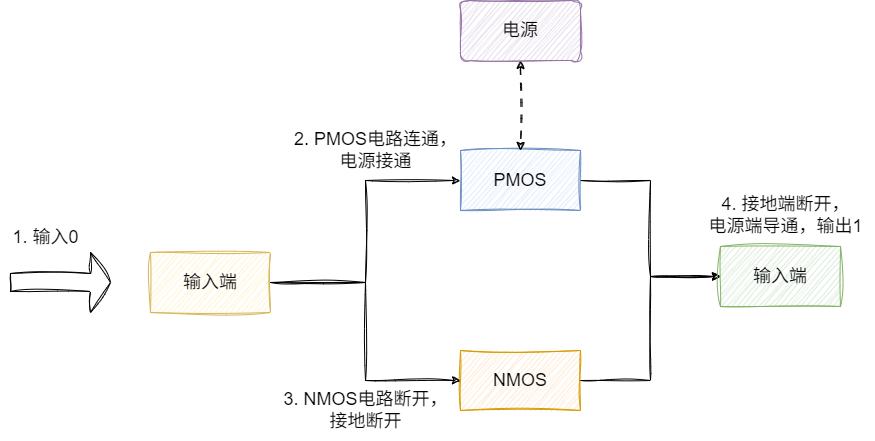
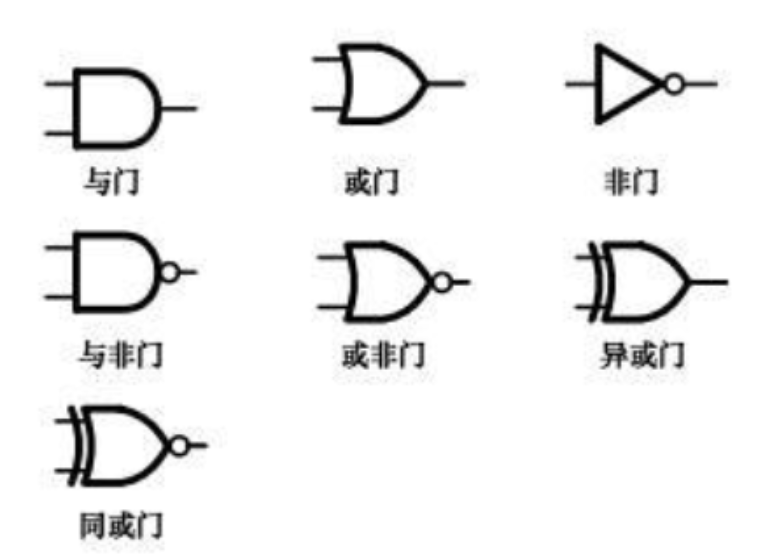
由此可知，輸出結果與輸入結果相反，就生成二進制中的非運算，而上述的組合我們也稱之為非門。同理，設計者們基于NMOS和PMOS這兩種晶體管搭建出各種各樣的門電路：

1. 與門
2. 或門
3. 非門
4. 與非門
5. 或非門
6. 異或門
7. …

邏輯運算下運算的實現

基于邏輯門的基礎，我們開始推進計算機運算的步驟，我們都知道計算機是二進制語言，對應我們以加法為例，對應的運算為：

1. 0+0=0 即二進制的00+00，最終輸出二進制結果為00
2. 0+1=1 即二進制中的00+01，最終輸出二進制結果為01
3. 1+1=2 即二進制中的01+01，最終輸出二進制結果為10

最終我們將這些數字的二進制運算轉為換下圖所示的表格，我們以1+1為例，可以看到輸出二進制結果為10，對應的低位為0，而進位為1，由此得出10。

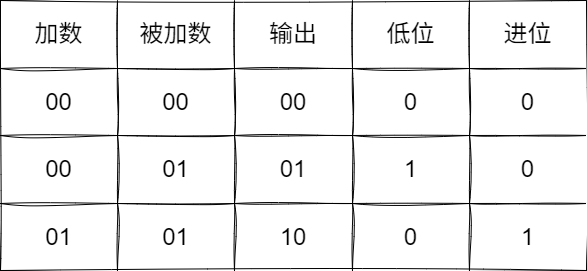
我們從最基礎的規律抓起，可以看到低位的0本質上不就是異或運算：

1. 第一行低位的0本質上就是 0^0，對應輸出0
2. 第一行低位的0本質上就是 0^1，對應輸出1
3. 第一行低位的0本質上就是 1^1，對應輸出0

然后我們就需要考慮另一個問題，即進位問題，經過推理發現本質上就是按位與，同樣結合表格可以看出，對應的進位本質上就是低位運算的按位與：

1. 第一行低位的0本質上就是 0&0，對應輸出0
2. 第一行低位的0本質上就是 0&1，對應輸出0
3. 第一行低位的0本質上就是 1&1，對應輸出1

最終我們完成低位的加法運算推導過程，即通過：

1. 異或門計算低位和
2. 與門計算進位

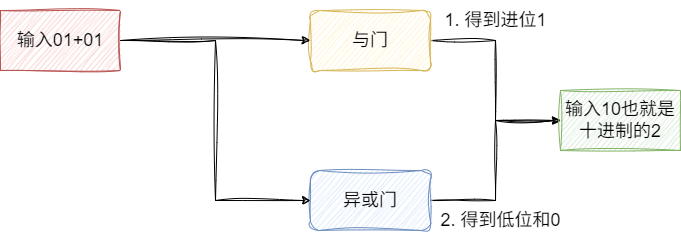
對應的我們將上述的邏輯視圖換成如下符號表示，讀者可結合圖片中的語義自行理解：

但是我們加法中還是涉及一些高位累加的，例如15+9對應9+5的進位就需要參與到高位的運算中，所以說我們目前的加法器只是一個簡單的半加法器。

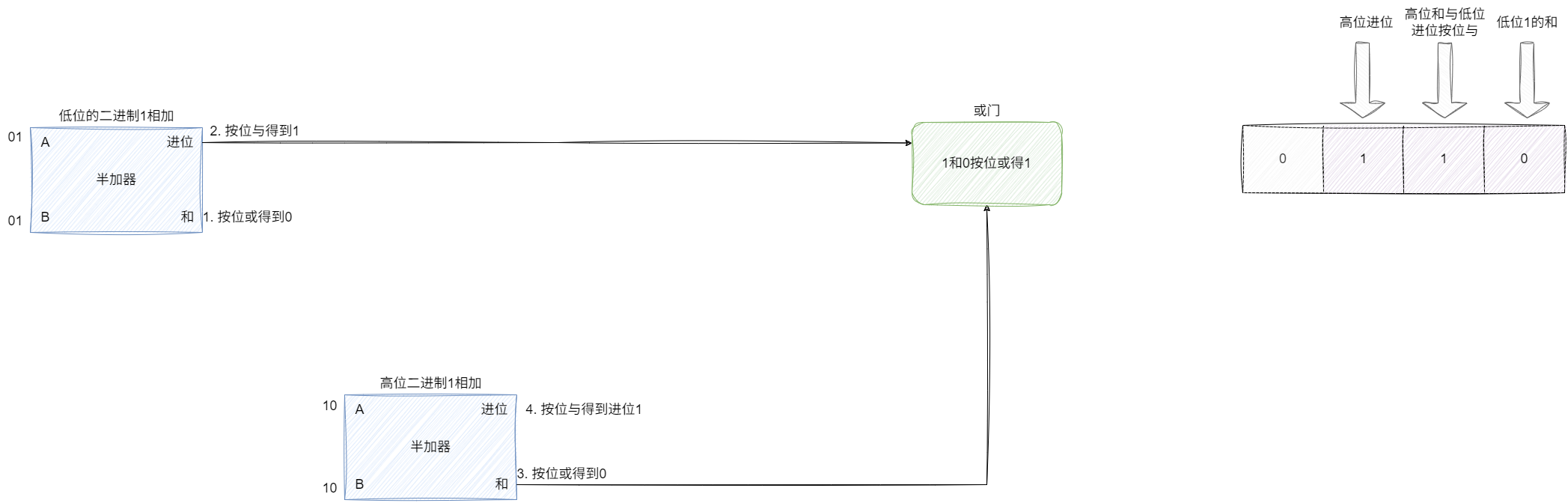
關于二進制進位的運算，通過低位進位和高位和進行按位或解決，我們試想3+3j即二進制的11和11相加，對應的換算步驟為：

1. 低位兩個1使用半加器算得和為0、進位1。
2. 高位兩個1使用半加器算得和為0、進位1。
3. 因為低位有個進位1，也就是10對應高位的和，兩者進行按位或得到1。
4. 結合低位和0，高位和和低位進位按位或得到1，高位進位1，得到二進制110也就是6：

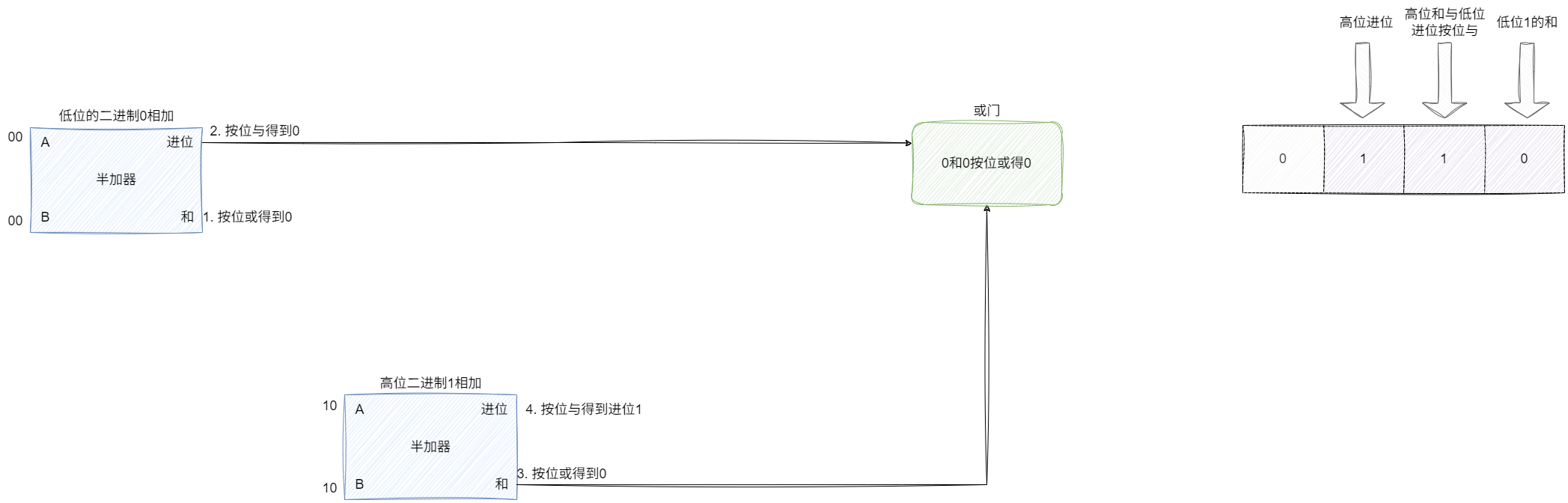
同理我們再演示一下2+2也就是二進制10和10相加：

1. 低位算得和0進位也為0
2. 高位算得和為0進位為1
3. 低位進位0和高位和0按位或得0
4. 結合低位0、高位和與低位進位0算法低2位為0，高位進位為1即100
5. 最終結果為4

通過這種運算，我們推理出全加法器，在此基礎上，串聯無數個全加法器生成更高進位的加法運算。