鋒哥原創的Scikit-learn Python機器學習視頻教程:
2026版 Scikit-learn Python機器學習 視頻教程(無廢話版) 玩命更新中~_嗶哩嗶哩_bilibili
課程介紹

本課程主要講解基于Scikit-learn的Python機器學習知識,包括機器學習概述,特征工程(數據集,特征抽取,特征預處理,特征降維等),分類算法(K-臨近算法,樸素貝葉斯算法,決策樹等),回歸與聚類算法(線性回歸,欠擬合,邏輯回歸與二分類,K-means算法)等。
Scikit-learn Python機器學習 - 特征預處理 - 標準化 (Standardization):StandardScaler
歸一化是基于最大值和最小值的,因此異常值(outliers)會對歸一化的結果產生較大影響。極端情況下,一個異常值可能會將整個特征的范圍壓縮到很小的范圍,從而導致其他正常數據的表示能力下降。
所以我們引入能夠盡可能降低異常值對數據處理結果影響的標準化計算操作。將特征縮放為均值為 0,方差為 1 的標準正態分布。
標準化(Standardization)公式是:
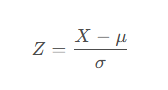
公式各部分詳解

工作原理
標準化將原始數據轉換為均值為0、標準差為1的標準正態分布。具體來說:

標準化的意義
-
統一量綱:將不同量綱、不同范圍的特征轉換到同一尺度上
-
中心化:轉換后分布的中心在0點
-
標準化尺度
:轉換后的值表示"偏離平均值多少個標準差"
-
Z = 0:表示該數據點恰好等于均值
-
Z = 1:表示該數據點比均值高出一個標準差
-
Z = -2:表示該數據點比均值低兩個標準差
-
在Scikit-learn中,使用StandardScaler進行標準化操作。
初始化 StandardScaler 對象時,有以下參數:
-
with_mean: boolean, 默認為 True-
作用:是否對數據居中(減去均值)。如果設置為 False,則不會減去均值,計算過程變為
x / σ。對于稀疏矩陣,設置with_mean=False是推薦且默認的,因為居中會破壞矩陣的稀疏性。
-
-
with_std: boolean, 默認為 True-
作用:是否將數據縮放到單位方差(除以標準差)。如果設置為 False,則計算過程變為
x - μ,只進行居中處理。
-
在調用 fit 或 fit_transform 之后,StandardScaler 對象會獲得以下屬性:
-
mean_:每個特征(列)在訓練數據中的均值(μ)。 -
var_:每個特征(列)在訓練數據中的方差。 -
scale_:每個特征(列)在訓練數據中的標準差(σ)。這是實際應用于transform的縮放比例。 -
n_samples_seen_:處理器在每個特征中處理的樣本數(用于在線計算均值/方差)。 -
n_features_in_:訓練時使用的特征數量。 -
feature_names_in_:訓練時使用的特征名稱(如果輸入的是 Pandas DataFrame)。
我們看一個示例:
import numpy as np
import pandas as pd
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler# 創建示例數據,包含不同類型的問題
data = {'age': [25, 30, np.nan, 45, 60, 30, 15], # 數值,含缺失值'salary': [50000, 54000, 60000, np.nan, 100000, 40000, 20000], # 數值,尺度大,含缺失值'country': ['USA', 'UK', 'China', 'USA', 'India', 'China', 'UK'], # 分類型'gender': ['M', 'F', 'F', 'M', 'M', 'F', 'F'] # 分類型
}df = pd.DataFrame(data)
print("原始數據:")
print(df)# 策略通常為 mean(均值), median(中位數), most_frequent(眾數), constant(固定值)
imputer = SimpleImputer(strategy='mean')# 我們只對數值列進行填充
numeric_features = ['age', 'salary']
df_numeric = df[numeric_features]# fit 計算用于填充的值(這里是均值),transform 應用填充
imputer.fit(df_numeric)
df[numeric_features] = imputer.transform(df_numeric)print("\n處理缺失值后:")
print(df)standard_scaler = StandardScaler()df_numeric = df[['age', 'salary']]
# 根據數據訓練生成模型
standard_scaler.fit(df_numeric)
# 根據模型訓練數據
df_standardized = standard_scaler.transform(df_numeric)print("\n標準化后的數值特征:")
print(df_standardized)
print(f"標準化后的方差:{df_standardized.std()}")運行輸出:
[[-0.68032458 -0.17837652][-0.30923844 0. ][ 0. 0.26756478][ 0.80401995 0. ][ 1.91727835 2.05132995][-0.30923844 -0.62431781][-1.42249684 -1.51620039]]數學知識,什么是標準正太分布:
正態分布的概率密度函數顯示為典型的鐘形曲線,這一形狀類似于寺廟中的大鐘,因此也常被稱為鐘形曲線。作為一種連續分布,正態分布擁有完備的概率密度函數、累積分布函數、矩生成函數和特征函數等表達形式,并且具備明確的期望(即均值)、方差、偏度和峰度等數值特征。
(我們可以參考動畫學習 正太分布 轉載自抖音成其老師)




)

)


)
、CommonJS(CJS)和UMD三種格式)
)
:高級實現——平衡源項、邊界條件與算法總成)
技術解析)


)


