---

1.摘要

本文提出了一種面向無人機（UAV）新型軌跡優化方法，以實現對地面移動節點的高效視覺覆蓋。與傳統方法不同，該方法顯式考慮節點的移動性，生成連續且平滑的三維飛行軌跡，更符合實際應用需求。研究目標是通過優化無人機軌跡設計，最大化任務執行過程中被覆蓋的節點總數。為降低無限解空間帶來的計算復雜度，本文首先利用 Bézier 曲線將連續的軌跡優化問題轉化為離散的控制點選擇問題，在保證軌跡平滑性的同時大幅簡化計算。隨后，基于矩陣差分進化算法（MDE）框架，提出了一種無人機軌跡優化算法，有效兼顧覆蓋性能與計算效率。

2.系統模型和問題表述

網絡模型

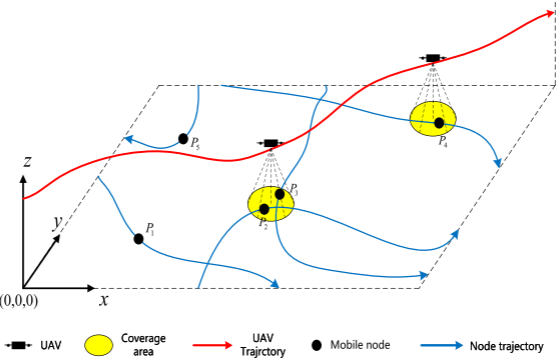
本文研究旋翼式無人機在二維平面上執行地面移動節點的視覺覆蓋任務。設平面內共有$n$個移動節點，每個節點均以一定速度沿各自的預設軌跡獨立運行。忽略節點間碰撞，第$i$個節點記為$P_i$，軌跡長度為$L_i$：
Q={qi(t)∣i∈[1,n],0≤t≤Tmaxe}\mathbf{Q}=\{\mathbf{q}_{i}(t)|i\in[1,n],0\leq t\leq T_{\mathrm{max}}^{e}\} Q={qi?(t)∣i∈[1,n],0≤t≤Tmaxe?}
V={vi∣i∈[1,n]}\mathbf{V}=\{v_{i}|i\in[1,n]\} V={vi?∣i∈[1,n]}

每個地面節點雖速度各異，但在運動過程中均保持恒定。無人機搭載圓形視覺傳感器，從初始點$(0,0,H_u)$起飛，以固定高度$H_u$沿平滑連續的軌跡飛行，最終抵達終點$(E_x,E_y,H_u)$完成覆蓋任務。

視覺覆蓋模型

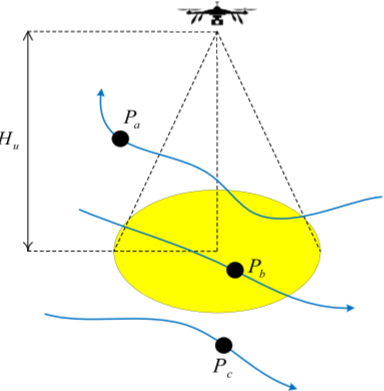
模型將節點簡化為沿軌跡運動的點目標，忽略其形狀與尺寸。為保證監測質量，每個節點需滿足最低分辨率要求。無人機采用定焦視覺傳感器，其分辨率與飛行高度成反比：高度越高，覆蓋范圍越大但分辨率下降。為兼顧覆蓋與能耗，無人機飛行高度取所有節點允許高度的最小值，并據此確定視場半徑。

問題描述

本文研究目標是確定一條最優無人機飛行規劃${\mathbf{q}}^{?}$，在一定約束條件下，使無人機視覺覆蓋的地面移動節點數量最大化。在任務執行時間內共覆蓋$S$個地面易懂節點：
$$S=\sum _{i=1}^n{S}_i$$

優化目標可表述為：
$${\mathbf{q}}^{?}=\arg \underset{T\le T_{cs}\le T_{\max }^e}{\max }S$$

限制無人機在三維空間$\Omega$內運動：
$$\Omega =\left\{\begin{array}{cccc}v=(x,y,z)\in {\mathbb{R}}^3& 0\le x\le E_x,& 0\le y\le E_y,& 0\le z\le H_u\end{array}\right\}$$

3.矩陣差分進化算法

由于優化問題為非凸難以實時求解，本文提出基于矩陣差分進化算法（MDE）框架，該方法在DE的基礎上，引入矩陣化候選解表示與參數更新機制，便于并行計算與協同優化，其核心流程包括初始化、變異、交叉與選擇四個步驟。

將控制點坐標向量化，上下界：
$$\mathbf{U}=\left[\begin{array}{c}{E}_x,E_y,E_x,E_y,?,E_x,E_y\end{array}\right]$$
$$\mathbf{L}=[0,0,0,0,?,0,0]$$

種群變異

本文采用DE/rand/1方式，比例因子在MDE中用矩陣表述：
$$\Lambda =\lambda {\mathbf{F}}_{N\times D}$$

構造供體矩陣為：
$${\mathbf{Y}}^g={\mathbf{X}}_{[{\mathbf{r}}_1,?]}^g+\mathbf{\Lambda }°\left({\mathbf{X}}_{[{\mathbf{r}}_2,?]}^g?{\mathbf{X}}_{[{\mathbf{r}}_3,?]}^g\right)$$

種群交叉

交叉算子主要參數是交叉率，比例因子：
$$\Gamma =\gamma {\mathbf{F}}_{N\times D}$$

控制點種群矩陣:
$${\mathbf{W}}^g={\mathbf{Y}}^g°\mathbf{\Phi }+{\mathbf{X}}^g°\overline{\mathbf{\Phi }}$$

種群選擇

定義適應度函數$fit:{\mathbb{R}}^{N\times D}\to {\mathbb{R}}^{N\times 1}$，貪心保留種群。新一代種群生成：
$$X^{g+1}=W^g°(B_z\times F_{1\times D})+X^g°(\overline{B_z}\times F_{1\times D})$$

4.結果展示

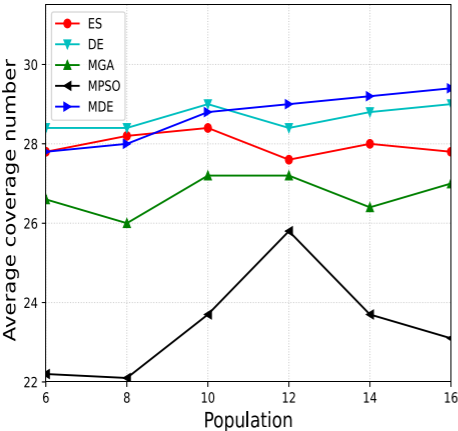
5.參考文獻

[1] Jia R, Li H, Sun P, et al. UAV trajectory optimization for visual coverage in mobile networks using matrix-based differential evolution[J]. Knowledge-Based Systems, 2025: 113797.

6.算法輔導·應用定制·讀者交流

xx