原題鏈接
原題再現
題目描述
給定一個?n?個點?m?條邊有向圖，每個點有一個權值，求一條路徑，使路徑經過的點權值之和最大。你只需要求出這個權值和。
允許多次經過一條邊或者一個點，但是，重復經過的點，權值只計算一次。
輸入格式
第一行兩個正整數?n,m。
第二行?n?個整數，其中第?i?個數?ai??表示點?i?的點權。
第三至?m+2?行，每行兩個整數?u,v，表示一條?u→v?的有向邊。
輸出格式
共一行，最大的點權之和。
題意簡述
有向圖，點都有點權。點可以經過多次，但點權只能加一次。
求這張圖的最大權值。
解題思路
如果一個強連通分量上的某個點被選中，那么選擇整個強連通分量顯然更優。因為這樣可以最大化點權總和。這樣一來，可以把整個強連通分量視為權值為強連通分量中所有點權值之和的整體點，選擇這個強連通分量上任意一點就意味著選擇整個強連通分量。所以縮點。
縮點，也就是將強連通分量合并為單點，將原來k個強連通分量的圖簡化成只有k個點的有向無環圖（DAG）。Tarjan算法實現。
Tarjan算法
在DFS搜索遍歷整個圖的過程中，把有向圖劃分為DFS搜索樹及非樹邊。
與傳統的DFS不同的是，多了回溯這一步。
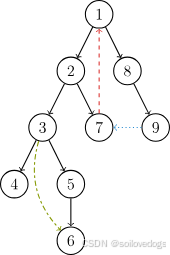
非樹邊可以被分為：
- 返祖邊（回邊）：從樹上的后代指向祖先，如7→1。
- 橫叉邊：無直接祖先關系且分屬不同子樹，如9→7。
- 前向邊：從樹上的祖先指向后代，如3→6。
在遇到非樹邊時，有相應的操作。
如果結點 u 是某個強連通分量在DFS搜索樹中遇到的第一個結點，那么這個強連通分量的其余結點肯定是在DFS搜索樹中以 u 為根的子樹中。結點 u 被稱為這個強連通分量的根。
關鍵數據結構
- 數組dfn：dfn[i]表示第一次發現i的時間戳，亦可判斷是否為被訪問。
- 數組low：low[i]表示i的追溯值，u或u的子樹能夠追溯到的最早的棧中節點的次序號。
- 數組vis：vis[i]表示i是否正在訪問，即是否在棧中。
- t：時間戳。
- scc：強連通分量個數。
- 棧st：棧保存了當前深度優先搜索（DFS）路徑上的所有節點。這些節點可能屬于同一個強連通分量，但尚未確認是否構成完整的SCC。用于追溯。
- 數組color：每個節點標記其所屬的強連通分量編號。
void tarjan(int v) {dfn[v] = low[v] = ++tot; //標記dfn[]訪問順序，還有low[]的初始值sta.push(v); //讓點v進棧vis[v] = true; //標記這個點被訪問過for (int i = head[v]; ~i; i = edge[i].next) { //一直循環這個點每一個出度，直到-1表示沒有了，這也是為什么memset head數組時要賦-1int u = edge[i].to; //定義u并把它賦成這條邊的終點if (!dfn[u]) { //如果u沒有被訪問過tarjan(u); //找下面這個點low[v] = min(low[v], low[u]); //這個點low[v]的值就是當前low[]的值與找到的u點的low[]值} else if (vis[u]) //如果u被訪問過了，但是還在隊列中low[v] = min(low[v], dfn[u]); //low[v]就取這個點的low值與循環到的點u的dfn[u]的最小值}if (dfn[v] == low[v]) { //如果發現v這個點的dfn[]和low[]相等，說明這個點是一個強連通分量的“根”。sccnt++;int u; //定義u變量，作為棧頂元素do { u = sta.top(); //將u賦值為sta棧的棧頂元素vis[u] = false; //將u彈出sta.pop(); //同上color[u] = sccnt; //將u標記為這個強連通分量里的點} while (v != u); //當v == u之后，結束循環}
}
參考文獻
強連通分量 - OI Wiki
速通Tarjan與強連通分量
全網最最詳細！一文講懂Tarjan算法求強連通分量&縮點 - 淼畔 - 博客園
tarjan算法詳解--關于圖的連通性 & 連通分量 - 知乎
tarjan算法總結 (強連通分量+縮點+割點)，看這一篇就夠了~_強連通分量切割-CSDN博客
淺談 tarjan-騰訊云開發者社區-騰訊云
Tarjan-1972.pdf
深入淺出 Tarjan 算法 (一)
60 分鐘搞定圖論中的 Tarjan 算法（一） - 知乎
寫在最后
說實話，我作為初學者，學這個算法的時候挺吃力，看了不少網上的算法書（原因就是把算法書全都忘在學校了QAQ），可能是鄙人智力有限的原因吧。所以我決定自己錄一個視頻，演示一下這個過程。
)
